利用相邻测线重叠区域进行多波束测深横摇运动残差改正

王俊森，金绍华，边志刚，边 刚

（1.海军大连舰艇学院，辽宁 大连 116018；2.交通运输部北海航海保障中心天津海事测绘中心，天津 300222）

多波束测深系统采用面状测量的模式，是目前获取海底地形测量数据的主要技术手段[1-3]。该系统是计算机技术、导航定位技术和数字化传感器技术等多种技术的高度集成[4]，其测量数据质量受海洋环境影响较大，因此需要配置辅助传感器获取姿态、声剖、航向、潮汐等多种数据，对测深值加以改正，通过数据后处理获取更高精度的测量结果。影响多波束测深数据质量的系统性误差主要有多波束换能器自身测量误差、姿态测量误差、声线跟踪误差、表层声速误差、水位改正误差等[5-6]。国内外学者对这些影响因素进行了较为深入的研究并提出了相应的改正方法。边缘波束误差是影响多波束测深数据精度的主要因素[4]，本文聚焦边缘波束的横摇运动残差改正，分析多波束声线追踪模型、姿态改正模型、表层声速等改正方法，削弱多波束自身的边缘波束误差，提高测深数据的整体质量。

在多波束姿态改正方面，国内学者逐步建立了声线跟踪后处理模型，即先通过声线跟踪获取波束点坐标，而后通过姿态旋转矩阵改正波束点位置[3，7-9]；如今有学者提出声线跟踪前，顾及姿态影响下的高精度波束入射角改正方法[10-11]，姿态改正模型从二维平面分析进入到三维空间建模分析，使得多波束测深数据姿态改正的精度得到进一步提高。目前姿态改正主要针对在测量过程中对测深值影响较大的横摇、纵摇和艏摇，升沉变化对测深的影响也得到学者们的关注[12-14]。在表层声速误差改正方面，朱小辰等[15]研究了表层声速误差对测深值的影响，揭示表层声速误差对测深值的影响实际上是改变波束指向角；董庆亮[16]从理论上分析表层声速对多波束系统的影响，论证在实际测量中采集表层声速的重要性；肖付民等[17]推导表层声速误差影响下的波束指向角与点位归算误差模型，对表层声速误差做了定量化的研究。在声线跟踪方面，目前普遍采用高精度的常梯度法声线跟踪法获取水深值[1，10]；理想状态下，多波束换能器的波束断面与水面、航向正交，姿态换能器获取的测船姿态数据，用于消除测量过程中海面动态起伏对测船的影响[9]。实际作业过程中，一般采用姿态传感器与换能器分开安装的方式，姿态传感器与多波束换能器位置之间存在偏移，需要注意测船姿态与换能器姿态的区别[8]，因而姿态传感器测量的不是实际换能器的实时姿态[18]，由此产生的运动残差对多波束测深数据质量也有影响。张永厚等[18]提出一种利用横摇规律提取横摇运动残差的方法，建立了横摇运动残差与水深值之间的关系并加以改正，取得了良好的效果。

上述文献多是针对单一误差源进行分析并提出改正方法，对各种误差之间的耦合关系及其共同影响效果未加以深入研究。海上测量的动态性和不可重复性，难以对海底地形重复观测，这给校正地形数据中的误差带来困难。姿态误差、表层声速误差、运动残差等误差均对中央波束影响较小，对边缘波束影响较大[10，15，19]，中央波束的测量精度高于边缘波束[19-20]。当多波束对海底地形进行精细化探测时，测线间距较小，相邻两条测线之间会出现较大的重叠度。因此可以使用一条测线的中央波束来改正相邻测线的边缘波束水深值，提高多波束测深数据的整体质量。

在影响多波束测深数据质量的诸多误差中，运动残差尤其是横摇运动残差的影响最大且最容易被识别[3]，其存在使得多波束数据边缘波束产生“波浪”起伏效果[18]；通过上述误差分析可知，姿态误差、表层声速误差、运动残差等均会对波束入射角产生影响，通过斯涅尔定律作用于声线跟踪的全过程[17]，导致多波束测深点位置和水深出现偏差。遵循这一思路，本文提出一种利用中央波束校正边缘波束综合误差的模型，将姿态误差、表层声速误差、运动残差等误差通过中央波束与边缘波束的比对，得出各种误差综合影响下的边缘波束测深误差；通过推导横摇运动残差改正模型求得横摇运动残差补偿角，使用精密的补偿公式消除各种误差对波束入射角的影响。

1 模型建立

本文模型流程如图1 所示。相比边缘波束，中央波束受误差影响小、测深点数据质量高。当相邻两条测线具有较高重叠度时，一条测线的边缘波束会覆盖相邻测线的中央波束，因此可以使用中央波束来提高边缘波束的测深质量。首先，使用沿航向的测深点匹配插值模型，将边缘波束点与中央波束点匹配得到对应的匹配点对，计算各种误差综合影响下的边缘波束测深误差值。将边缘波束测深误差值输入横摇运动残差模型，计算得到横摇运动残差补偿角，然后通过波束入射角精密补偿公式，得到误差补偿后的波束入射角，最后进行常梯度声线跟踪得到改正后的测深值。

图1 模型流程图

1.1 沿航向的测深点匹配插值模型

多波束测深点依靠Ping 数与Ping 内的波束号进行索引。若两条测深条带存在公共部分，则公共位置存在两次测量的点对，即匹配点对[21]。若一测线中央波束点表示为n；k =1，2，3，…，256），相邻测线边缘波束对应的匹配点对为测深点l=1，2，3，…，256），其中i、j 表示测深点位于对应测线中的Ping 数，k、l 表示Ping 内的波束号。理想情况下，测船航速稳定，作业时不考虑姿态影响，测深仪器Ping 率稳定，所得数据Ping 之间、Ping 内测深点分布较为均匀。这种情况下，如式（1）所示，一条测线中央波束第i 至i+n 的Ping 数据与相邻测线的边缘波束j 至j +n 的Ping 数据相匹配；测线的中央波束某一Ping 内的第k 点应与相邻测线的边缘波束的某一Ping 内的第l 点相匹配，两匹配点对的水深值应保持一致。

考虑到两条测线对公共位置的覆盖，理想条件下匹配点对的位置是重合的，可将平面距离最近的两个测深点认为是对同一位置的测量，因此匹配准则为最小距离准则。

获取匹配点对后，通过式（3）计算得到边缘波束测深误差值。

模型通过匹配点对得到边缘波束测深误差值驻Zj，进而求取运动残差对应的波束入射角改正量。值得注意的是，横摇运动残差会导致波束点水平位置偏移，因而未进行横摇运动残差改正之前，用于寻找匹配点对的水平位置带有偏差。在测深点匹配前，本模型假设水平位置是准确的。

实际作业中，考虑到测船航速变化、实时姿态、仪器Ping 率变化等因素，多波束Ping 数据之间、Ping 内测深点之间分布不均匀。这种情况下，在式（3）匹配准则约束下，会出现中央波束与边缘波束匹配，中央波束与边缘波束匹配的情况，如式（4）所示，导致边缘波束第i + 1 的Ping 数据未能匹配到中央波束，因而也就无法通过式（2）求取边缘波束测深误差值驻Zj+1。本文模型重点关注中央波束与边缘波束Ping 数据的匹配，对于Ping 内数据点的匹配，例如与的匹配依靠式（2）准则约束，此处式（4）忽略Ping 内数据点的变化。

边缘波束测深误差值驻Zj+1缺失导致无法得到相应Ping 的横摇运动残差补偿角，因此需要对横摇运动残差补偿角进行插补缺失值。本模型使用三次样条函数插补缺失值。三次样条函数连续光滑的曲线物理模型具有很好的拟合效果[22]，使用其插补缺失值已经得到广泛应用[22-23]。将Ping 号与横摇运动残差补偿角分别作为自变量与因变量进行三次样条函数拟合，插值补充缺失Ping 的横摇运动残差补偿角。

多波束测深系统误差具有多源性，覆盖同一位置的中央波束测深点与边缘波束测深点互差得到的水深值驻Zj，包含了姿态误差影响水深值驻Zm、表层声速误差影响水深值驻Zssp、运动残差影响水深值驻Zmr和其他影响边缘波束测深质量的误差影响水深值驻Ze在内的多种误差影响量。因此，沿航向的测深点匹配插值模型得到的边缘波束测深误差值可表达如下。

沿航向的测深点匹配插值模型得到的边缘波束测深误差值包含各种误差的综合影响。一方面，不同误差的影响及其相互间耦合作用，使得难以单独分析每种误差对测深误差值的贡献；另一方面，各种误差诱发因素并不相同，建立各种误差综合改正模型使得公式复杂难以解算。考虑到诸多学者已经证实运动残差中的横摇运动残差对测深值影响最大[18]，其存在导致边缘波束呈现上下起伏波浪状。因此，聚焦运动残差中对测深值影响最大的横摇运动残差，对边缘波束加以改正。

1.2 横摇运动残差改正模型

多波束测深数据经过声线跟踪、固定安装偏差改正和姿态改正，将数据从换能器坐标系转换到测船坐标系再转换到当地水平坐标系。目前，姿态改正方法主要有两种，一种是先通过声线跟踪获得波束点坐标，尔后通过姿态角构建的旋转矩阵进行强制旋转变换[11]，该方法使用来自换能器的波束入射角，将声线追踪与姿态改正视为独立的过程，割裂了波束入射角与横摇角、纵摇角之间的关系。另一种是考虑了横摇对入射角的影响，波束入射角为换能器提供波束入射角与横摇角之和，该方法将横摇、纵摇视为独立的过程，未能顾及纵摇及横纵摇耦合作用影响。事实上，测船横纵摇姿态均会对波束入射角产生影响，分析各姿态角及其耦合作用对波束入射角的影响至关重要。现阶段精密声线跟踪已经考虑姿态角及其耦合作用对波束入射角的影响。横摇运动残差是横摇角的残余量，可以通过姿态角对波束入射角的影响公式直接进行补偿。首先进行姿态改正，公式如下。

式中，琢、茁、酌分别为测船实际的横摇角、纵摇角和航向角；R（琢）、R（茁）、R（酌）分别为对应的旋转矩阵。对式（6）展开得到当地水平坐标系下的水深值ZLLS。

考虑到船体实际横纵摇角琢、茁与横纵摇观测值R、P 之间的关系[11]。

将式（8）带入式（7）中，考虑存在横摇运动残差的情况下，得到了横摇运动残差影响下的水深值改正量。

令式（5）所得边缘波束测深误差值与式（9）中横摇运动残差影响下的水深值改正量相等。

即可求出边缘波束第j 个Ping 数据对应的横摇运动残差驻Rj。文献[10]中提出一种顾及姿态角的波束入射角确定方法，该方法综合考虑了横纵摇对波束入射角的影响，显著地提高了多波束测深的精度。考虑存在横摇运动残差的情况下，确定波束入射角的公式如下。

式中，兹j 为换能器提供的波束入射角；兹j忆为经过姿态和横摇运动残差改正之后的波束入射角。

式（11）为波束入射角的精密补偿公式，获得波束入射角之后，通过常梯度声线跟踪模型[1，10]，得到多波束测深点在当地水平坐标系下的坐标，完成横摇运动残差的改正。

2 实例计算与分析

试验数据来自某海域外业实测数据，采用的是R2sonic2024 浅水多波束系统，水深约14～16 m 左右。使用Caris 软件对水深数据声速改正、姿态改正和潮汐改正后，查看数据发现本次测量任务测线间重叠较大，一条测线的边缘波束覆盖到另一条测线的中央波束。查看测线的侧向水深剖面，发现中央波束数据地形较为平坦，而边缘波束围绕中央波束呈现明显的上下“起伏”，起伏幅度约为0.5 m，初步判断是运动残差导致的测深误差。为验证本文方法的有效性，设计如下实验。

选取两条相邻测线重复压盖的区域大约1 000 Ping 数据，如图2 所示，本试验以2 号测线中央波束来改正1 号测线右侧边缘波束作为计算实例，1号测线中央波束改正2 号测线左侧边缘波束按照同样的步骤操作。

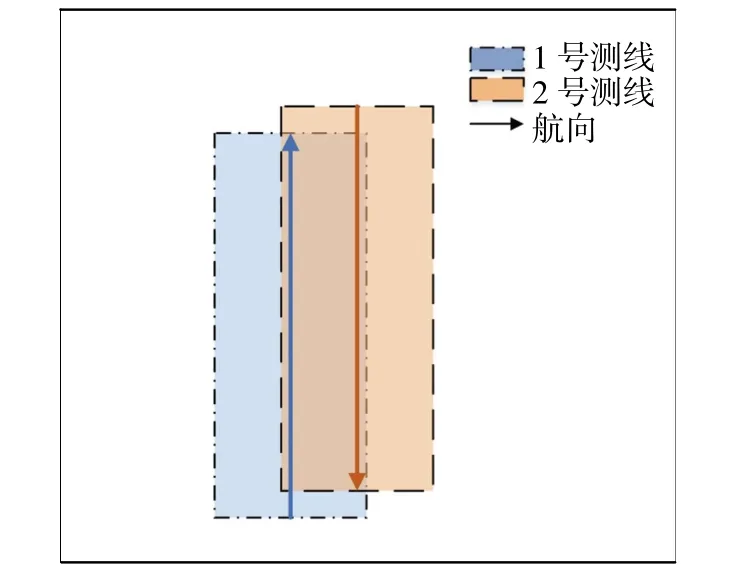
图2 两条测线位置示意图

首先使用沿航向的测深点匹配插值模型。选取2 号测线第128Ping 数据作为中央波束点，在1 号测线的测深点中寻找匹配点对，使用三次样条函数拟合插补缺失值。表1 显示两条测线匹配点对平面位置情况，共完成945 对测深点的匹配，其平面位置差异均值在0.067 m 左右，最大值在0.269 m 左右，小于《海道测量规范》（GB 12327—2022）对水深测量中水深点的平面位置极限误差（置信度95%）的规定[24]，因此可以认为在这种水平的平面位置偏移影响下，测深点的匹配是合理的。

表1 匹配点对的平面位置偏移情况统计

图3 是使用三次样条函数插补缺失运动残差补偿角的情况。拟合的曲线通过原有的数据点，能够较好地刻画连续状态下运动残差补偿角，确保插补的缺失值有较高的可信度。图4 显示了经过姿态改正的1 号测线边缘波束（深蓝色）、2 号测线中央波束（橙色），上述两条曲线由Caris 软件声线追踪得到；图4 同时比对了传统直接补偿公式（青色）与顾及姿态角的补偿公式（紫色）对1 号测线边缘波束的校正。特别说明的是，由于2 号测线中央波束（橙色）、传统直接补偿公式（青色）与顾及姿态角的补偿公式（紫色）数据差距很小，也印证了两种补偿公式的有效性。因而作图时将传统直接补偿公式（青色） 向上平移0.1 m，将顾及姿态角的补偿公式（紫色）向下平移0.1 m 以示区分，其具体数值见对应颜色的纵轴刻度。

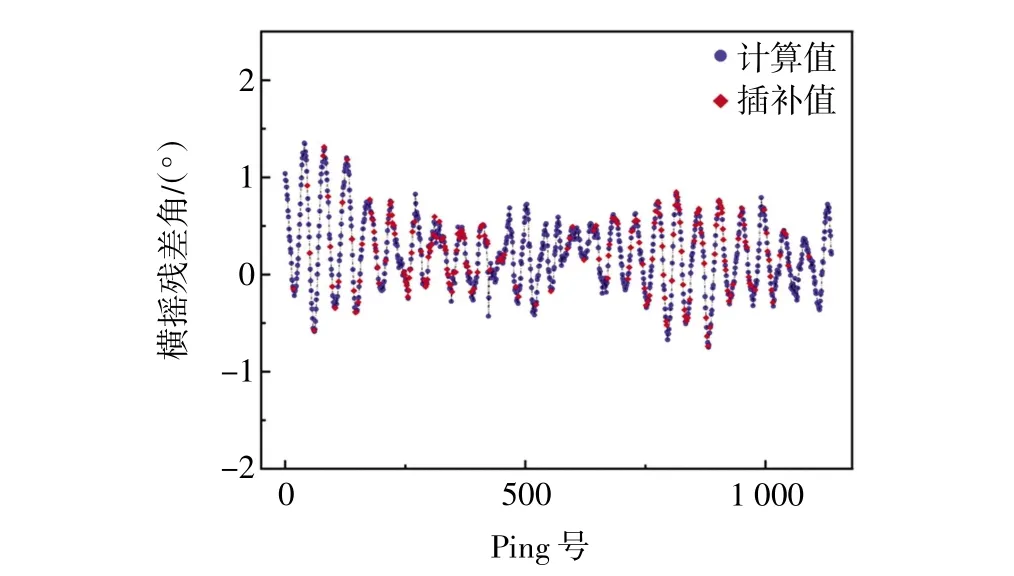
图3 三次样条函数插补缺失值

图4 边缘波束与中央波束对比图

由图4 可知，1 号测线边缘波束（深蓝色）围绕2 号测线中央波束（橙色）呈现明显上下起伏的形态，为运动残差中横摇运动残差未完全改正所导致。将两者做差得到的边缘波束测深误差值代入到横摇运动残差改正模型中，使用Python 科学计算Sympy 库求解非线性方程（9）的解析解，得到运动残差补偿角。接着使用式（11）重新计算波束入射角，根据新分配的波束入射角进行常梯度声线跟踪，得到的测深值跟踪结果与原始数据、中央波束数据对比见图4。计算波束入射角直接补偿公式（即波束入射角为波束分配角与姿态角之和）与2 号测线中央波束的差值数据A 和本文的顾及姿态角的精密补偿公式与2 号测线中央波束的差值数据B，并统计差值的均值、方差、中位数、极小值和极大值等数据，见表2。

表2 两种补偿公式与2 号测线中央波束水深值差值统计单位：m

图4 中2 号测线中央波束（橙色）、传统直接补偿公式（青色） 与顾及姿态角的补偿公式（紫色）3 条曲线重合度较高。从表2 可以看出，两种模型跟踪出来的水深值与中央波束水深值差异不明显，其均值与标准差均较小。传统直接补偿公式和顾及姿态角的补偿公式对声线跟踪的水深值影响最大值不超过2 cm，远小于《海道测量规范》（GB 12327—2022）规定的误差允许范围[24]。从式（11）分析可知，当纵摇角茁较小时，cos 茁接近于1，式（11）可近似成为直接补偿公式。本次数据纵摇角平均值为0.52毅，最大值为1.57毅，因此两个公式差异较小。当纵摇角较大时，应当予以考虑。

横摇运动残差影响多波束换能器发射声波时的空间姿态，整Ping 测深数据均受到其影响，通过匹配点对求得横摇运动残差可以改正对应的整Ping 测深数据。下面选取约200Ping 较为平坦的海底地形数据，对其进行改正。图5 和图6 分别表示改正前后的海底三维地形。图5 中沿航迹向上下起伏的海底地形，经过本文模型的改正，在图6 中边缘波束起伏幅度减小，海底地形趋于平坦，更为接近真实的自然海底地形。

图5 改正之前的海底地形

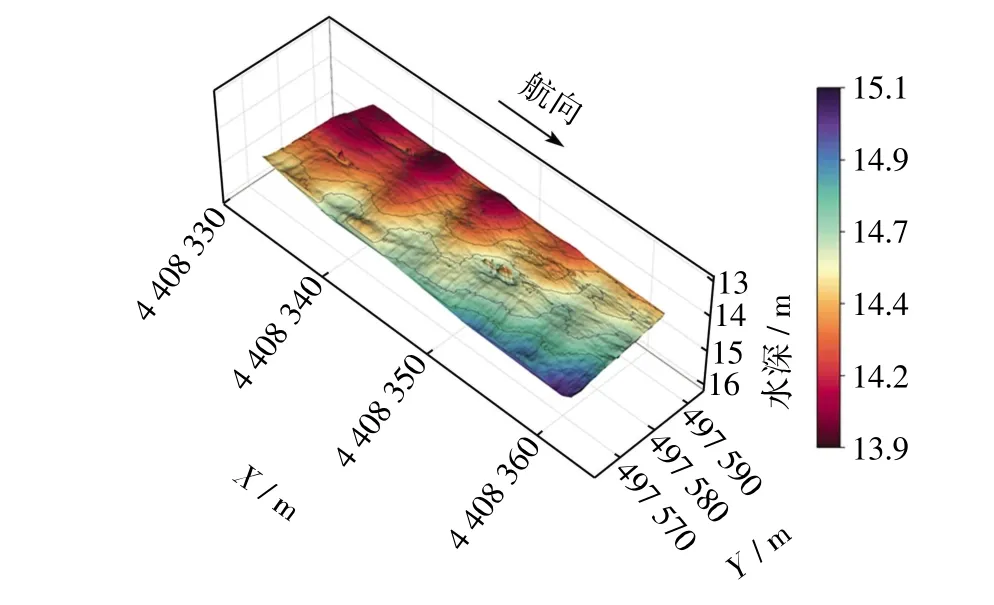
图6 改正之后的海底地形

真实海底地形是自然连续的，统计一定范围内的水深点，其分布应该遵循正态分布规律，区域出现特征物或者虚假地形会破坏水深点的正态分布规律。以0.1 m 为间隔统计位于不同水深区间的水深点数量，则改正前后水深点的水深区间分布如图7所示。橙色代表改正之前的水深值统计，绿色代表改正之后的水深值统计。改正之前的水深点在14.1 m 附近出现了峰值，观察相邻测线的海底地形，该区域没有水下特征物，因此可以推断该区域存在虚假地形，即边缘波束呈现规律性的上下起伏。改正之后的水深点统计区间消除了改正之前的14.1 m 处的峰值，水深点的分布范围更集中，符合正态分布，验证了本文算法的有效性。

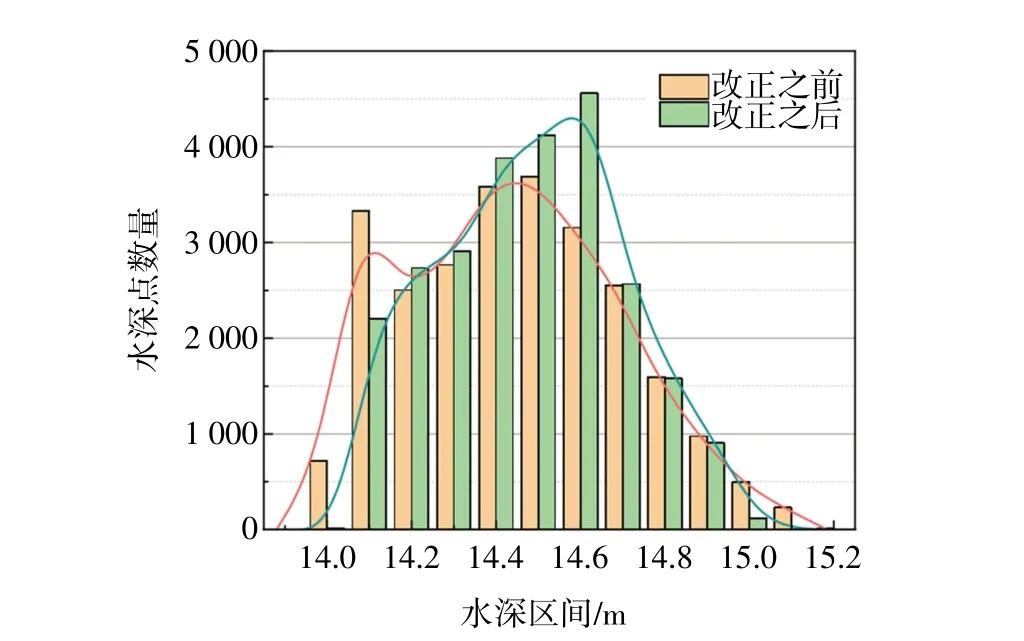
图7 改正前后水深点统计

根据试验数据的重复区域，统计本文算法改正前后交叉点水深不符值情况，如图8 和图9 所示，并给出改正前数据C、改正后数据D 交叉点水深不符值的平均值、标准差、中位数、最小值和最大值，见表3。从交叉点水深不符值数量统计来看，改正之后交叉点水深不符值分布区间明显变小，数据分布更集中，消除了由于横摇残差存在导致的姿态改正不完全情况。

表3 交叉点水深不符值统计单位：m

图8 改正之前交叉点水深不符值

图9 改正之后交叉点水深不符值

3 结 论

本文提出一种利用相邻测线重叠区域进行多波束测深横摇运动残差改正模型，该模型能够在相邻条带有较高的覆盖率情况下，修正条带边缘波束的测深值以横摇残差为主的各项误差。使用沿航向的测深点匹配插值模型，实现了相邻测线中央波束测深点与边缘波束测深点的配对；推导了顾及姿态角的波束入射角精密补偿公式，实现了对边缘波束测深值的校正，削弱了多波束测量过程中边缘波束的横摇运动残差、姿态测量、表层声速等误差的影响，提高了多波束边测深条带边缘波束的质量，具有较高的实际工程应用价值。

需要指出的是，姿态角和运动残差也会对波束点的平面位置产生影响，本文的沿航迹向匹配插值模型忽略了这种影响，认为平面位置相对准确，这会导致本文的匹配模型出现一定的误差。下一步将进一步研究姿态角和运动残差对波束点平面位置的影响，完善中央波束测深点与边缘波束测深点的匹配插值模型。