海底管道局部冲刷研究综述

闫 莎,刘名名,王浩丞,金瑞佳,李曦宁,王 铭

(1.中国石油大学(北京),北京 102249;2.聊城大学,聊城 252000;3.成都理工大学,成都 610059;4.交通运输部天津水运工程科学研究所,天津 300456)

海洋油气资源开发和海洋油气经济的发展,缓解了近年来掠夺性开采陆地油气资源而引起油气资源枯竭这一问题[1]。因此,近年来随着世界各国对海洋油气资源开发的重视,海底管道运输的发展产生了明显飞跃。根据中海油能源经济研究院发布的《中国海洋能源发展报告2021》,海洋油气生产已成为关键的能源增长极,海上油气等化石能源将成为驱动能源发展的主要动力。海底管道作为海洋油气的主要运输通道,尤为关键地影响海洋油气开发作业的优劣性,要提高海洋油气资源的利用率,必须不断发展海底管道相关研究工作,吸收关键技术,稳步提高我国海底管道技术水平[2]。

相较于陆地管道所处的环境而言,海底管道所处的环境条件更为极端。海底管道铺设于相对复杂的海洋环境中,大多管道又需要埋设于海床面下一定深度,因此检查维修等作业很难进行,而部分管段又处于潮差区或波浪破碎区(特别是立管),更容易遭受波浪、潮流、冰凌等严重冲击,有时甚至可能遭受海洋中漂浮的坚硬物体或船舶撞击产生破坏,以及遭受抛锚破坏,从而造成海底管道的严重破坏,导致管道失效破漏,造成油气泄露,引发海洋环境和海洋油气经济的双重危机。导致海底管道破坏失效的主要因素包括：海底床面运动、波浪及水流冲刷作用[3]。海底管道在海洋水动力因素和海底床面运动等相互耦合作用的长期影响下,管道周围的泥沙等沉积物极易受到侵蚀和迁移,使得管道下方的海床周围发生大规模的侵蚀,附近的泥沙等沉积物在不断冲刷剥蚀下被掏空,管道下方出现悬空现象,从而使管道极易受到损坏,大幅降低管道的使用周期。

综上所述,要使海洋油气资源开发安全有效地进行就要保证海底管道的安全和稳定,因此开展海底管道局部冲刷研究显得尤为重要。如何通过开展海底管道局部冲刷研究,尽可能真实地模拟和还原出海底管道局部冲刷过程,获得管道周围冲刷坑的形态和高度,成为保障管道安全运行、维护海洋油气资源和海洋环境安全的一项重要命题,对海洋油气资源开发战略具有重要的实际工程技术意义,也具有重要的科学研究价值。

1 海底管道局部冲刷过程概述

海底管道铺设于海床面时,管道周围的流场结构会在来流经过管道时瞬间产生变化,管道周围的来流强度会显著增加甚至在周围出现旋涡。由于来流强度的增加以及旋涡的出现,原本泥沙不发生运移的海床可能开始出现泥沙运移的情况,对于本就存在泥沙运移现象的海床而言,海底管道的存在会进一步加强泥沙运移的强度,从而形成冲刷现象,这种冲刷称之为海底管道局部冲刷(图1和图2)[4]。海底管道局部冲刷现象存在时,管道下方就会出现冲刷坑,且冲刷坑的深度随着冲刷时间的延续而不断增加,从而导致管道悬空,严重危害管道安全,因此,开展海底管道局部冲刷方面的研究十分必要。海底管道局部冲刷研究所关注的问题包括以下3类：泥沙起动机理研究、泥沙运移问题研究、渗流问题[5]。

图1 海底管道布置图Fig.1 Schematic diagram of submarine pipeline

图2 管道周围冲刷坑形态Fig.2 Scour profile around the pipe

(1)泥沙起动机理研究。泥沙起动机理研究是开展海底管道局部冲刷研究的首要关键点。泥沙起动研究从本质上讲,就是研究水流作用下泥沙开始起动的条件,受泥沙颗粒自身固有的性质、泥沙颗粒所处位置以及泥沙同水流两者之间相互作用等多种因素影响,该问题的研究一直是该研究领域的前沿课题。非粘性沙起动冲刷时主要受自身有效重力和流体作用力(即切应力和上举力)作用,而粘性泥沙除了受到上述2个力作用外,还受到颗粒间粘结力的影响。对于非粘性泥沙,考虑泥沙启动问题需考虑流体作用带来的流体启动和重力作用阻止泥沙运动这两者间的关系,而对粘性泥沙来说,粘性细泥沙在淤积固结条件下会形成一定的稳定结构,颗粒间粘结力增大,成为抗拒水流冲刷力的主要因素。因此考虑粘性泥沙启动问题时就不能忽视淤积固结条件下粘性细泥沙形成的稳定结构和颗粒间粘结力。迄今,科学研究和工程应用方面主要采用下列3种方式来判定泥沙颗粒是否起动,即起动拖曳力(又称切应力或者剪切力准则)、起动流速准则、起动功率准则[6]。针对非粘性泥沙的启动,目前研究上应用最广泛的是时空平均临界希尔兹剪应力(拖曳力)理论,即河床来流作用下的剪切力(拖曳力)[7]大于泥沙起动所需要的剪切力时,泥沙就会在水流作用下开始起动,否则泥沙颗粒保持静止,冲刷现象也不会发生。θcr为临界希尔兹参数,由下式定义

θcr=θcr0(cosα*+sinα*/tanφ)

(1)

式中：α*为海底坡度倾角;φ为泥沙的休止角;θcr0为平坦海床面上的临界希尔兹参数,可以由SOULSBY等提出的相关公式求解

(2)

式中：D*为无量纲的泥沙粒径。

(2)泥沙运移问题研究。学者通过研究提出,泥沙颗粒按照其运动形式的不同,可以分为接触质、跃移质、悬移质及层移质4个部分。对于均匀、非粘性泥沙来说,运移主要可以分为2种方式,即推移和悬移[8]。泥沙启动后,多以滚动和滑动形式运移,成为推移质运输;随着流速的增加,部分泥沙运移仍以推移质为主,另一部分则开始悬浮,以悬移质运动。当然也可能存在颗粒较细的海岸底部浮泥运动和颗粒较粗的海岸底部推移质运动。2种运移方式可能随时会发生转变。泥沙运移形式受泥沙自身性质影响,具有“粘性”的泥沙运移形式和均匀、非粘性泥沙的运移形式存在出入,较小粒径的粘性泥沙主要偏向于悬移质运输。

(3)渗流问题。海底管线上下游存在一定的流体压差,使流体从高水头到低水头,因而使管线下部流体流速较大。在流体流动过程中,土体会对流体产生阻力作用,而流体也会给土体一种反作用力,即渗流力。渗流力将会带走土体,致使位于管线下部的土体发生管涌现象[9]。实验结果表明,对于非粘性底床来说,管涌现象是造成海底管道冲刷的主要原因。管涌和涡流共同破坏了管道附近床面的平衡,这标志着冲刷的开始。

值得说明的是,上文所提出的相关公式均来自于均匀、非粘性泥沙的冲刷实验,本文后续所建立的方程也主要是针对于均匀、非粘性泥沙底床而言。粘性泥沙颗粒之间的粘性效应难以考虑,因此目前针对粘性泥沙底床冲刷的研究相对较少[10]。然而海底环境复杂,管道所经过海域的绝大部分海底底质以淤泥质为主,研究粘性底床的海底管道冲刷特性,对真实海底管道冲刷问题预测具有重要意义。

此外,管道下方冲刷坑形态及最大平衡深度也是研究海底管道局部冲刷的重要问题。迄今,已有诸多学者对此方面开展了研究,研究发现平衡冲刷深度对整个冲刷过程及管道后方出现的旋涡脱落现象起着较大的作用。研究同时发现,粘性底床的冲刷深度还会受稠度系数的影响。管道下方的冲刷深度在上游水流携带的泥沙颗粒量与河床面向下游输送的泥沙颗粒量一致时达到最大深度,并将其命名为平衡冲刷深度。

基于以上对于海底管道局部冲刷不同问题的研究,有学者提出可以将海底管道局部冲刷的整个过程分为4个阶段,即：(1)初始冲刷阶段：由于来流作用,管线上下游存在一个压力差,压力差会使流体给床面一个渗流力。土体随渗流力的增加不断被带走,管线下方开始出现管涌现象,从而造成悬空,这一阶段称为初始冲刷阶段;(2)孔道冲刷阶段：随压力差的不断增加,在上一阶段形成的管涌现象将从管道后方延伸于前方,从而在管道下方出现孔道。孔道处水流流速很快,泥沙便会通过孔道不断向管道后方冲刷,而且在管道后方逐渐集聚,形成小规模沙脊,在管道下方形成冲刷坑;(3)尾迹冲刷阶段：随着时间的推移,冲刷深度不断加剧,当海床与管道的间距达到某一值后,管道尾迹区就会发生尤为显著的旋涡脱落过程。由于旋涡脱落现象会进一步增加同床面的剪应力,下游管道的冲刷现象将更剧烈。尾迹涡具有一定的周期性,所以观测到的位于尾迹区内的泥沙推移现象也具有周期性;(4)平衡冲刷阶段：随着冲刷的进行,尾迹涡逐渐趋于稳定,冲刷坑的深度和形态也趋于稳定,床底表面冲刷形态也大致保持不变,该阶段为平衡冲刷阶段。现阶段对于海底管道局部冲刷的研究,大多集中在尾迹冲刷和平衡冲刷阶段的研究(图3)。

图3 管道周围冲刷过程Fig.3 Scouring process around the pipe

2 国内外研究现状

目前,世界各国的研究学者针对海底管道局部冲刷开展了很多工作,主要采用的方法大致可以分为以下3类,即理论分析、模型试验以及数值模拟。前期阶段,由于计算机发展的诸多限制,学者多通过模型试验的方法来研究问题。关于海底管道局部冲刷的模型试验开展了比较丰富的研究,得到了比较丰硕的成果,但模型试验取得的结果无法与技术实践相结合并加以验证[11]。数值模拟法随着计算机发展的不断完善也开始进一步走向成熟,能够与理论分析、模型试验等方法相结合,直观有效地再现海底管道局部冲刷的全过程,从而可以更好地预测冲刷坑深度和形态等,促进了关于海底管道冲刷的科学探究和实际应用。下文将按照理论分析、模型试验、数值模拟等3类不同方法来概述国内外研究发展历程及现状。

2.1 理论研究

海底管道局部冲刷通常会涉及到一些物理过程,如来流运动、管道动荡、泥沙输送等,以及发生于所涉及到的物理过程之间的强耦合作用[12]。海底管道局部冲刷是多学科交叉研究的一个前沿课题,受多种复杂系统所响应,关于海底管道局部冲刷的研究由来已久,下列主要以时间发展为脉络,对具有代表性的海底管道局部冲刷理论研究进行纵向概述。

早在20世纪60年代,HERBICH等[13]对埋藏于海底的海底管道稳定性和管道周围存在的冲刷现象展开了研究,并提出新的思路预测海流作用下海底管线下方的冲刷深度。KJELDSEN[14]最先开展了针对海底管道局部冲刷问题的实验研究,发现冲刷平衡深度受到管道几何尺寸和来流速度的显著影响,并提出了一个预测冲刷平衡深度、管径和来流速度三者间关系的经验公式,从而更加丰富地完善了关于海底管道局部冲刷这一课题的理论体系。LUCASSEN[15]在KJELDSEN[14]的研究基础上对该问题进行了更深层次的研究,并进行了丰富和优化,提出了隧道冲刷和尾涡冲刷2个过程,并且考虑了冲刷受泥沙颗粒大小的影响。自20世纪80年代末以来,世界各国的众多专家学者就海底管道局部冲刷这一问题开展了大量深入性的研究工作。其中,MAO[16]提出海底管道上下游之间在海洋来流作用下将会出现一个压力差,这种压力差将会致使流体对土体的渗流力产生,虽然这种渗流力不足以使砂体运动,却会加剧来流对砂体的冲刷。SUMER等[17]则发现了床面与震动管线在洋流作用下的相互作用关系,以及冲刷如何受管线尾部湍流的影响,并且得到了一个拟合公式可以用于冲刷平衡深度的计算。CHIEW[18]研究讨论了单向定常流条件下海底管道局部冲刷的作用原理以及预防冲刷发生的方法,通过探讨得到局部冲刷受来流对土体渗流作用的影响,但管道周围存在的涡流以及由压力差引起的管涌效应才是导致局部冲刷发生的首要因素。此外,只有在管道上下游的压力梯度大于泥沙颗粒的悬浮重力时才会发生局部冲刷。CHIEW提出一个与给定流动条件下的函数可以预测给定流量和几何边界海底管道的最大冲刷深度。阎通等[19]以堤北海域水下三角洲的地质条件及现实工况为依据,对埋置管道和裸置管道进行研究,对比分析两者稳定性强弱,通过计算预测埋置管道冲出掩埋所需要的时间以及管道下的最大冲刷平衡深度。MYRHAUG和RUE[20]则根据SUMER所研究的用于计算最大平衡冲刷深度的经验公式,进一步推导出了新的经验公式可以用于计算海底管道冲刷坑在随机波浪作用下的宽度和深度,并且可以用于计算位于桩附近的冲刷坑深度。潘冬子等[21]进行了海底管道局部冲刷在波载荷作用下的研究,发现了波载荷作用下冲刷发生的临界条件、冲刷机理及冲刷形态,将局部冲刷过程分为管道周围产生旋涡阶段、管道下方开口阶段、管道下方掏空阶段、旋涡趋于稳定阶段、冲刷平衡稳定阶段5个阶段,并推导出了管道平衡冲刷深度与KC数及相对埋深的经验公式。杨兵等[22]就海洋来流、海底管道和海床三者间的耦合作用通过采用量纲分析法,展开了研究探讨,从而建立海底管道周围局部冲刷的相似准则。

2.2 模型试验

早期计算机水平有限,并且因为冲刷是一个循环往复的过程,来流所形成的冲刷坑容易被泥沙颗粒等沉积物重新填充,在工程开发上想要现场观测冲刷坑的形态和最大深度比较困难,因此研究海底管道局部冲刷相关问题时现场试验比较少,大部分研究局部冲刷的方法是在实验室里面得到的。迄今为止,国内外有许多学者通过在实验室环境下建立物理模型,对海底管道模型进行了一系列成功的局部冲刷试验,通过这些物理实验可以更加直观有效地观测海底管道局部冲刷的全过程。下文根据模型试验研究侧重点的不同以及按照模型研究时间进展,从横向和纵向上分别选取对海底管道局部冲刷的具有代表性的模型试验进行阐述。

首先对来流作用下管道局部冲刷的模型试验研究大多是根据已建立的实验室内试验模型来探讨海底管道局部冲刷特性同其影响因素之间的关系,从而可以推导出相关经验公式来表示各个影响因素同最大冲刷平衡深度之间的关系。代表性人物有：KJELDSEN[14]最先采用模型试验的方法进行有关海底管道局部泥沙冲刷问题的研究工作,通过实验发现了海底管道的冲刷深度受海底管道几何尺寸、来流速度等因素的影响且该影响不可忽视,并且开创性地提出了揭示海底管道下方冲刷深度、海底管道几何尺寸、来流速度三者之间关系的经验公式。LUCASSEN等[15]在KJELDSEN的实验基础上加以改进,研究发现了泥沙粒径大小对冲刷过程的影响,并得出随埋深比的增加,平衡冲刷深度将会减小的结论。IBRAHIM和NALLURI[23]进行了试验模拟并对实验所得结果进行了分析探讨,得出了临界希尔兹参数对冲刷的影响,根据临界希尔兹参数的大小,冲刷问题应该可以分为清水冲刷(θ<θcr)和动床冲刷(θ>θcr)两类,其中θcr为临界希尔兹参数。在清水冲刷条件下,只有管道附近才会发生冲刷现象,距离管道较远处冲刷现象都不会存在;而在动床冲刷条件下,整个管道周围的床面都将会发生冲刷现象。MAO[16]进行了一系列研究海底管道局部冲刷的模型试验,特别是极具代表性的水槽试验,与海底管道局部冲刷实验研究形成对比。CHIEW[24]则采用试验模型的方法对含导流板的管道在海底局部冲刷现象的相关问题展开了分析探讨,研究发现,带有导流板的管道在海底局部冲刷的程度和深度将会有所增大,管道自埋发生的速度也更快。SUMER[25]就清水与动床2种不同的冲刷情况展开了试验对比研究,分析研究结果得出,底床切应力系数在清水冲刷条件下,对管道下方的最大冲刷深度有显著影响;但动床冲刷条件下对其无显著影响。随着认识的不断深入,三维实验研究也不断加以发展。CHENG等[26]建立了三维试验冲刷模型,通过试验研究了管道在不同的埋置深度、来流速度和迎流角情况下对横向冲刷的影响,研究发现管道横向冲刷速度随着埋置深度的增大而减小,随着来流速度的增大而增大。国内学者针对这一问题进行了很多研究,杨兵等[27]对海底管道周围海床冲刷问题进行了实验模拟,并展开系统研究,通过实验研究分析了局部冲刷的作用原理以及冲刷坑最大平衡深度等,并对已有的成果进行总结和分析。吴钰骅等[28]进行了海底管道水槽模型试验,研究了海床上泥沙的起动机理并阐述了间隙比对砂床流速的影响。臧志鹏等[29]开展了单向流条件下海底管道冲刷的三维研究工作,研究侧重于探讨海底管道纵向冲刷速率如何受不同来流速度、管道最初埋深深度和来流迎角的影响。常留红[30]通过试验研究在不同动力条件下,不同作用角时三维管道冲刷的影响因素以及冲刷过程,并给出了冲刷平衡经验公式。杨少鹏等[31]通过控制变量法进行了单向流条件下的试验研究,探讨了平衡冲刷深度受海底管线安装阻流器与否的影响以及受间隙比差异的影响,研究发现,管线附近流场的分布和冲止流速是决定冲刷深度大小的关键所在,并得出了在安装阻流器且存在间隙比时用于计算平衡冲刷深度的经验公式。

以上实验模型主要是针对单向流情况下进行的,而对于铺设于海洋环境中的海底管道,波浪对管道的作用也不可忽视。迄今,也有许多专家学者就波浪条件下海底管道冲刷的相关问题进行了一系列模型试验研究。CHIEW[32]通过实验研究了海底管线上阻流板的安装对波浪作用下管道下方的冲刷深度和程度以及冲刷速度的影响。SUMER和FREDSØE[33]采用实验的方法探讨了在波浪条件下海底管道下方的最大冲刷深度和KC数两者间的关系。秦崇仁等[34]采用波浪水槽对不同水深、不同管径、不同泥沙颗粒大小进行了模型试验,得到了波浪作用下冲刷开始发生的条件以及冲刷的广度和深度。李玉成等[35]进行了模型试验研究了波浪作用条件下海底管线上的水平力、举力等,并通过实验分析探讨了波浪作用条件下海底管线附近所处流场以及流场特性是如何影响作用于管线上的力。SUMER等[36]对海流波浪作用下的埋置于海床下的海底管道局部冲刷的临界条件做了实验研究,研究发现,海底管线下方出现的渗流速度增加会造成管涌现象,而管涌现象正是造成局部冲刷的主要因素。NEELAMNI和RAO[37]研究了埋置于黏性土中的管线在波浪作用条件下管线附近的冲刷情况。夏令[38]采用波浪水槽物理模型试验对不同工况下海底管道下方形成的冲刷坑深度展开了系统研究,研究得到了冲刷坑最大深度和KC数之间的拟合关系。潘冬子和王立忠等[39]进行了波浪水槽物理模型试验研究,探讨了在波浪条件下海底管道产生局部冲刷的作用原理和床面冲刷形态以及平衡冲刷深度的大小等。ZANG等[40]假定了波浪、稳定流作用下管道开始出现局部冲刷现象的临界条件,并依此建立了波浪和稳定流作用下的数值波浪水槽。孙国民[41]在基于瓯江口海域的工程基础上,建立了考虑波浪作用的二维潮流泥沙数学模型,计算得到了滩面最终平衡状态下的冲刷深度。

除单向流和波浪情况外,振荡流对海底管线冲刷的影响仍然不能忽视,一些学者也做了该方面的实验研究。浦群等[42]利用抽气式“U”型振荡流水槽产生的周期性振荡水流,用该振荡流代替波浪从而研究振荡流对砂质、淤泥质海床面的侵蚀,并在实验完成后进行海床面冲刷深度大小的测定。羊皓平[43]进行了一系列针对海底管道冲刷的实验研究,通过实验探讨了海底管道冲刷现象造成管线附近流场及水动力特征的改变,并探讨了振荡流条件下管道冲刷的机理。殷俊等[44]对原型尺寸下管道振动、泥沙颗粒运动和底床运动的耦合问题展开了相应研究。

总体而言,海底管道冲刷的物理模型实验研究往往侧重于单向流情况下,而对处于波浪和振荡流条件下的海底管道冲刷现象的模型实验研究较少。研究该问题的专家学者希望可以通过建立物理模型开展实验,从而探寻出预测管道下最大平衡冲刷深度的经验公式,但现实情况是由于实验条件和模型选取存在差异性,导致目前现有的经验公式在公式表现形式和最终预测结果上大都存在较大出入。现将学者所研究的经验公式整理如表1所示[45]。其中,S为管道的平衡冲刷深度;U为水流流速;g为重力加速度;D为管道直径;d为泥沙粒径;Ucr为平均流速;h为水深;H为波高;L为波长;θ为希尔兹数;e0为管道距离初始床面的高度。

表1 冲刷深度经验公式表Tab.1 Empirical formula of scour depth

2.3 数值模拟

近年来,由于计算机技术的高速发展和持续优化,计算流体力学(CFD)方法在此基础上也开始有了陡增式的发展,数值模拟方法不断优化,在科学研究领域和工程开发领域都得到了极大应用,也逐渐作为极为有效的工具应用于海底管道局部冲刷领域的研究中,预测模拟海底管道冲刷过程从而更好预测冲刷深度等一系列关注的问题,世界各国的专家学者针对海底管道局部冲刷方面的数值模拟也做了大量研究工作。目前常用的计算流体力学软件包括 Fluent、Simcenter STAR-CCM+、OpenFOAM、COMSOL、FLOW-3D等[46-48]。

预测管道下数值泥沙冲刷模型的方法大致分为两类,一类为平衡泥沙冲刷模型,通过迭代得到平衡冲刷面,这种方法可以有效地预测平衡冲刷坑,但却不能模拟海底床面从冲刷开始到平衡的演化过程;另一类为泥沙质量守恒法,该方法同样可以准确地预测出平衡冲刷河床形态,并且可以模拟床面从冲刷开始到冲刷平衡的演变过程。但是,质量守恒方法较平衡泥沙冲刷方法而言需要更多的时间。如今,随着计算机的不断发展,模拟技术的计算能力显著提高,泥沙质量守恒方法逐渐成为主流的求解方法。因此,研究中常采用泥沙质量守恒法来模拟床面的演变过程,控制方程如下所示

(3)

式中：yb为海床高程;p0为泥沙孔隙率大小;qT为总的泥沙输送率,包括悬移质泥沙输送率和推移质泥沙输送率。

悬移质泥沙输送率由下式计算求得

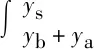
(4)

式中：qs为悬移质泥沙输送率;ys为波浪自由面的高度;ya为参考水平高度,以下为推移质输沙,以上为悬移质输沙,文中取ya=2.0d50,其中d50为泥沙颗粒的中值粒径;yb为海床高程;c为悬移质泥沙的体积浓度。

推移质泥沙输沙率的计算采用1987年由Van Rijin提出的下列公式

(5)

式中：qb为推移质泥沙输送率;s为流体中的泥沙密度与流体密度的比值,定义为s=ρs/ρ,其中ρs为计算采用的泥沙密度;ρ为流体密度;其中T0为无因次过剩层剪应力。

根据水流的不同形态采用的不同理论,又可以分为势流冲刷模型和湍流冲刷模型。海底管道局部冲刷方面的数值模拟由来已久,早在20世纪80年代,便有部分专家学者提出将数值模拟方法应用于海底管道局部冲刷方面的研究并开始付诸实践。CHAO等[49]最先采用数值模拟方法对海底管道冲刷以及海床面间存在的间隙等相关问题展开了研究,利用势流模型计算出了河床底部剪应力以及临界剪应力,并通过比较两者的大小判断是否达到冲刷平衡。当两者相等时,冲刷达到平衡。HANSEN[50]在无粘假定的基础之上提出了一种势流模型,并利用该模型进行了海底管道局部冲刷的数值模拟分析。如FREDSØE和HANSEN[51]建立了势流模型进行研究,采用修正VON MüLLER法建立流场模型,泥沙输运方程只考虑了沉积质,最终模拟结果表明该模型对管道冲刷坑中上游部分预测较好,但却未能预测管道冲刷坑下游。BERNETTR等[52]建立势流模型进行数值模拟,模拟研究了波浪作用下的海底管道冲刷,并准确预测出了冲刷坑深度。实际上管道中的水流主要以湍流模式存在,势流模型无法反映真实的流体状况,能够精确地预测出管道上游的地形特征以及最大冲刷深度,但却无法准确预测出管道下游后方的地形特征,这是因为势流模型无法模拟后方形成的尾涡。正如LI和CHENG[53]所提出的观点,势流模型的该局限性主要是因为势流模型不能模拟海底管道后方的尾涡脱落现象,而管道下游所形成的地形关键是因为尾涡的脱落,因此从整体上来看,势流模型的准确性差强人意。势流模型开始逐渐被取代。

为克服势流模型应用于数值模拟时存在的局限性,湍流模型开始逐步发展,研究人员开始通过求解水流Navier-Stokes方程来构建海底管道局部冲刷过程研究的数值模型,并采用不同方法封闭N-S方程,目前应用广泛的有k-ε、RNGk-ε、标准k-ω、SSTk-ω模型。早期的湍流模型是在k-ε模型基础上建立的。LEEUWESTEIN等[54]建立了基于k-ε的湍流模型和泥沙输运方程,但发现通过泥沙输运方程计算得到的结果与实际冲刷地形存在很大出入,造成该问题的原因是在建立湍流模型和泥沙输送方程时只考虑了推移质的影响,而忽略了悬移质。SUMER等[17]使用离散涡方法进行了数值模拟对海底管道附近冲刷流场展开了研究。BEEK和WIND[55]采用k-ε封闭N-S方程进行湍流模型下的数值模拟,并同时考虑推移质和悬移质,数值模拟得到的结果和实验预测结果大致吻合,但下游的模拟效果仍然不够理想。这些研究都是以粘性流体力学理论为基础,并考虑了实际流体中的湍流效应,因此以上研究模型同势流模型相比可以更加准确预测管道尾流区的冲刷,相较于势流模型的不足之处有了极大改善,但前期的湍流模型尾流区的模拟结果同实际情况仍有较大出入。据此,BRØRS[56]提出采用标准k-ε湍流模型进行冲刷模拟,同时考虑了悬移质、推移质输运以及密度的影响,该模型针对圆柱绕流方面的模拟结果和实验得到的结果可以进行很好的契合,但未能模拟出管道后方尾涡的周期性脱落。李玉成等[57]提出一种新的求解方法,即采用三步有限元法和大涡模拟对海底管道周围流场进行离散化,并分别求得二维和三维条件作用于海底管道上的无量纲水平力和无量纲横向力,该模型预测的结果和试验结果可以很好地进行契合。LI和CHENG[58]用基于大涡模拟(LES)的方法封闭N-S方程,并建立相关的数值模型开展了针对于海底管道冲刷的模拟工作,通过大涡模拟的方法可以准确预测出管道后方尾流区的冲刷情况,并且得到的模拟结果可以和实验室结果很好的吻合。该方法不仅可以成功地模拟出海底管道周围的流场,而且相较于传统的模型可以得到更加精确的床面剪切力。LIANG和CHENG[59]在学者所建立的已有冲刷模型基础之上进行了发展完善,对比分析了k-ε、k-ω、SSTk-ω等湍流模型在管道周围冲刷流场中的模拟结果,并且基于模型进行数值模拟,准确预测了冲刷剖面。SMITH等[60]对流场进行了数值模拟。孙娅等[61]基于Navier-Stokes方程、k-ω湍流模型以及泥沙输运模型对海底管道局部冲刷进行了数值模拟,计算了稳态边界流情况下的海底管道局部冲刷。许文兵等[62]基于标准k-ω湍流模型进行数值模拟,研究了往复流作用下海底管道冲刷悬空机理,并基于有限差分法进行离散化,研究表明海底管线下方的冲刷坑在往复流情况下大致具有对称性。文君锋等[63]研究了冲刷深度随雷诺数和来流流速的变化情况,发现冲刷深度随着雷诺数和流速的增大而增大(图4和图5)。顾中浩[64]采用物理模型和计算流体力学相结合的方法,对管道周围流场的运动特性及冲刷坑的发展过程进行了数值模拟,利用FLOW-3D建立海底管道局部冲刷在定床和动床情况下的研究。

图4 相对冲刷深度随雷诺数变化图Fig.4 Variation of scour depth with Reynolds number

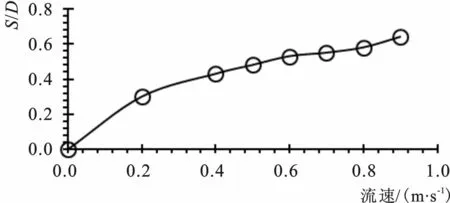
图5 相对冲刷深度随恒定流速变化图Fig.5 Variation of scour depth with flow velocity

上述海底管道冲刷的数值模拟工作大多是在单向流动的情况下进行的,由于波浪场的周期性和强湍流性,针对该方面的研究更为复杂、且难度更大,因此对于波浪条件下海底管道局部冲刷问题所开展的数值模拟可供借鉴资料很少。具有代表性的为LIANG和CHENG[65]利用有限差分方法求解N-S方程,建立了一个将波浪作用近似转变为振荡流的数值模型并进行数值模拟,该模型忽略了管道冲刷受波浪自由表面的影响。赵明[66]和ZHAO等[67]为克服振荡流未能考虑波浪自由表面对冲刷的影响这一局限性,便采用动网格技术开展了海底管线在考虑波浪自由表面情况下局部冲刷的数值模拟研究。FUHRMAN等[68]采用了类似于LIANG之前曾采用的方法,研究了振荡流条件下海底管道线冲刷的系列问题以及海底管道冲刷受KC数的影响。刘名名等[69]以及LIU等[70]通过求解利用SSTk-ω湍流模型封闭的Navier-Stokes方程组,实现了对海底管道在波浪作用下产生的局部泥沙冲刷的模拟。LIU等[71]实现了流体运动—管道振动—推移质输沙—悬移质扩散过程的全耦合动力分析,揭示了悬跨管道的振动响应与局部冲刷之间的相互影响作用,建立了悬跨管道振动幅值和冲刷深度之间的定量关系,阐明了其中的物理作用机理。LIU等[72]提出了近岸斜坡地形上海底管道局部泥沙冲刷深度预测公式,解决了国际知名管线冲刷专家SUMER教授提出的经验公式,仅适用于水下平坦地形的弊端。

总体而言,随着计算机技术的日益发展和诸多学者对海底管道冲刷这一问题深入研究,目前针对于海底管道局部冲刷研究的数值模拟方法比较全面广泛,研究成果也比较丰硕。但整体来看,针对于该问题的数值模拟研究大都是侧重于单向流条件下单管道的模拟,对于波浪以及振荡流作用下管道周围冲刷的研究,以及对海底背驮式管道、子母管道、海底并行布置两管道等多管道的研究较为欠缺。

3 结论与展望

综上所述,针对水流条件下的海底管道局部泥沙冲刷这一问题,世界各国专家学者均开展了广泛的研究实践,通过采用理论研究、试验模型和数值模拟等方法或多种方法相互结合的手段在该领域获得了丰硕的科研成果,并促使该领域的研究逐渐步入更完善的阶段。但是目前大多研究多集中于单向流情况下单管道附近的冲刷现象,针对往复流等其他情况下冲刷现象的研究还存在一些欠缺：

(1)针对二维管道冲刷研究较为完善,三维冲刷研究相对欠缺;

(2)单管道局部冲刷方面的数值模拟较完善,双管道、并行管道、子母管道等多管道研究相对欠缺;

(3)单向均匀流情况下的冲刷研究较完善,涡激振动下的振动管道局部冲刷研究,波浪自由表面影响作用下的管道冲刷研究较为欠缺;

(4)研究主要针对均匀、非粘性底床的海底管道冲刷,但实际底床为淤泥质,所以研究和实际工况存在一定出入。

总之,海底管道局部冲刷方面的研究还需要学者们进一步探索、丰富完善,对此展望如下：

(1)对神经网络等智能算法进一步优化,从而得到相较于经验公式预测更为精确的冲刷模型;

(2)对淤泥质底床冲刷进行进一步研究,从而更加接近实际海底管道冲刷;

(3)对于试验模型方面,若能获得更多实时数据来修正数值模型并应用于数值模拟,将试验模型和数值模拟进行实时有效对应,便能获得更精确的预测模型;

(4)从数值模拟角度来看,可以完善三维冲刷的研究来进一步提高精度,以及在模拟时考虑振动、温度、粗糙度等多因素对管道局部冲刷的影响。