窄缝挑坎射流轨迹及扩散特性试验研究
2023-09-07孙慧颖周家俞
孙慧颖,周家俞
(1.重庆交通大学 河海学院,重庆 400074;2.重庆交通大学 西南水运工程科学研究所,重庆 400016)
窄缝挑坎消能工通过急剧收缩出坎射流,使水舌实现了纵向和竖向的扩散,增强了水舌在空中的掺气和摩擦;入水后的水舌紊动扩散作用增加了单位水体的消能效率。我国的龙羊峡水电站、天生桥一级水电站及水布垭水电站等均采用了该消能方式[1-7]。
多位学者利用理论和试验等方式对挑流消能的射流轨迹进行了预测,并推导出有关挑距计算的理论公式。周茂林[8]采用抛掷体公式对水舌轨迹进行预测;张晓萍[9]基于传统水力学公式结合自由抛体理论并考虑空气阻力后得出挑距计算公式;傅长峰[10]以出射断面中心为原点建立了二维坐标系,按照斜抛自由水体考虑得出轨迹方程;姜志勇[11]基于《溢洪道设计规范》[12]规定的挑流水舌外缘挑距公式进行了气压修正,同时考虑空气阻力的影响,得出了基于气压与空气阻力共同影响下的挑距计算公式;张彦法等[13]考虑出射角、特征水深和综合影响系数等推测出水舌内外缘挑距计算公式。然而目前的研究缺少将断面出口高宽比作为考虑参数,本文就窄缝挑坎出口断面高宽比对水舌轨迹的影响进行讨论。
本文考虑窄缝挑坎出口断面高宽比及出口流速等对挑射轨迹的影响,基于物理模型试验,对现有挑距公式进行优化修正。修正公式考虑高速水流的挑坎出口断面宽度(高宽比)对水舌形态的影响,为便于确定同体型挑坎射流落点位置,避开下游的不利地质条件,同时为后续的雾化研究作基础[14-15]。
1 试验布置及方案
1.1 模型布置
本文基于某水电站窄缝消能工局部模型,该水电站采用混凝土重力坝坝型,窄缝挑坎消能方式。试验模型为正态模型,按重力相似准则设计,模型比尺为1:50。整个试验模型主要由有机玻璃制成,包括水箱、窄缝泄槽单体模型和下游水池等。挑坎部分由进口段、压力段和出口明流段组成。模型示意图如图1和图2所示:有压段高0.24 m,出口段高0.27 m,出口明流段采用半径为0.8 m的反射弧过渡,出口挑角为15°,窄缝收缩段进口宽度B为0.12 m,出口段宽度用b表示,将出口段高度h与出口段宽度b的比值定义为高宽比λ,即λ=h/b,根据不同工况等调整出口宽度b的大小控制高宽比。

图1 窄缝消能工模型布置示意图Fig.1 Model layout diagram of slit-type energy dissipator
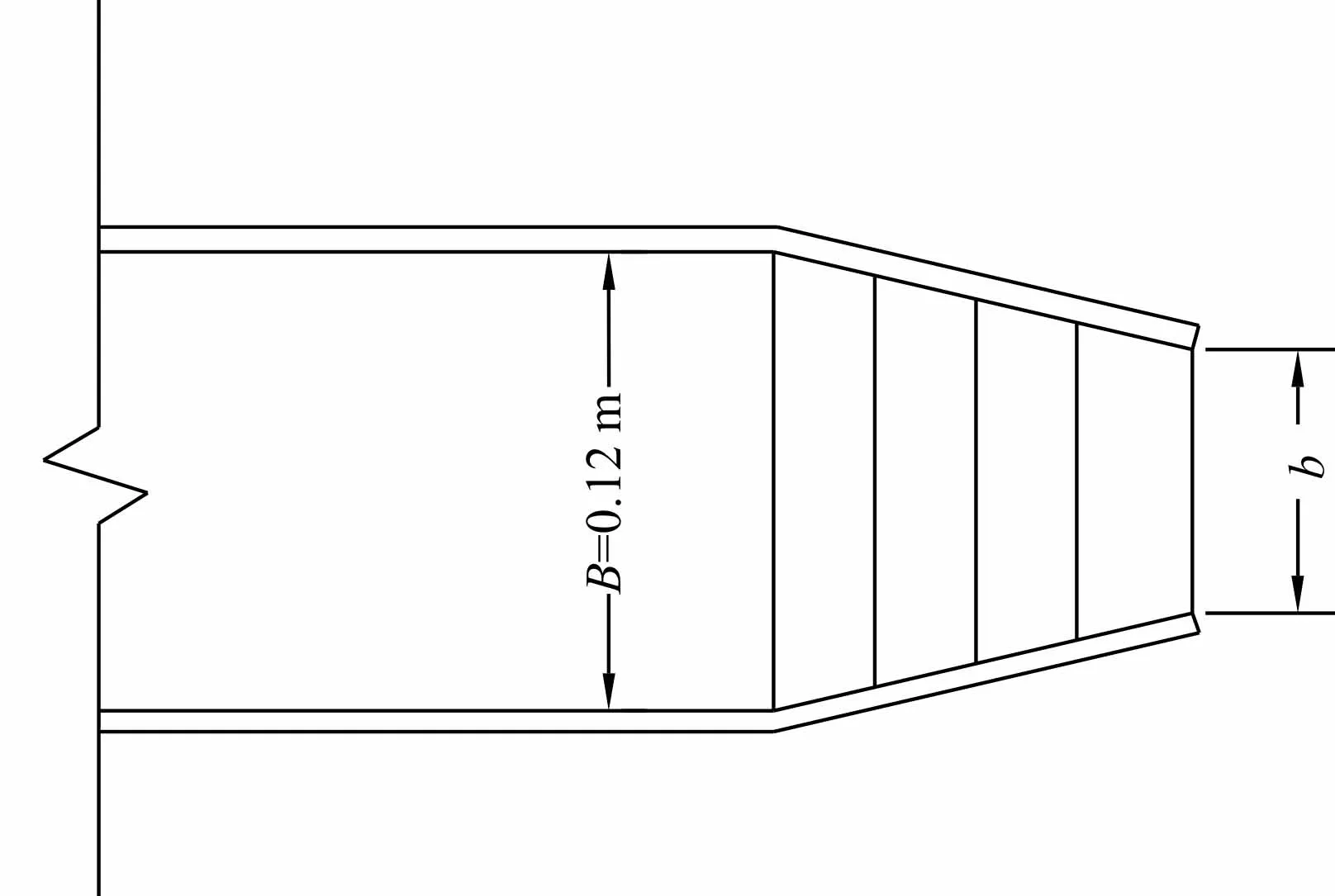
图2 挑坎俯视图Fig.2 Top view of bucket
1.2 试验方案
研究来流流量和高宽比λ变化对射流挑距的影响。试验方案如表1所示,试验通过调整出口断面的宽度b控制高宽比λ。为了使得数据更加直观,本文通过比尺换算后分别选取原型实际下泄流量250.10 m3/s、285.45 m3/s、336.00 m3/s、363.09 m3/s(设计洪水流量)、373.15 m3/s(校核洪水流量)作为试验流量,同时选取5种高宽比,共计25个工况。试验通过摄像法,利用相机拍摄挑流形态,在拍摄结果中选取效果最佳、最能体现该工况下水舌形态的水舌照片作后续分析。最后通过图形后处理确定水舌落水点、水舌内外缘挑距以及其对应的挑射角。
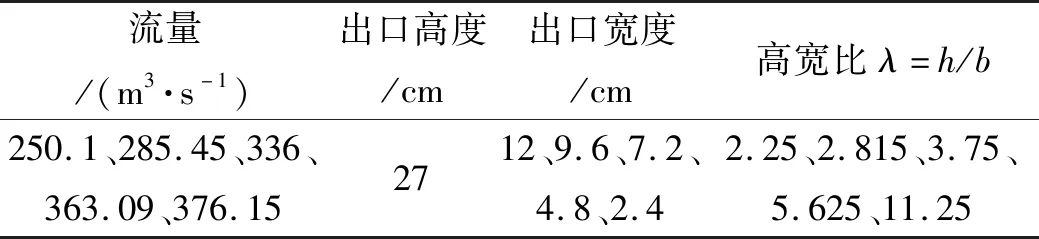
表1 试验方案布设Tab.1 Experimental working condition
2 试验结果与讨论
2.1 水舌形态
水舌出射角如表2所示,由表2可知,出射角随着高宽比的增加而增大。就窄缝挑坎而言,在来流流量Q恒为373.15 m3/s、高宽比λ自2.25增大至11.25的过程中,出射角自9.5°迅速增至41°,出射角增幅明显,变化范围达31.5°;而在高宽比λ为2.25、流量Q自250.10 m3/s增大至373.15 m3/s的过程中,出射角增量不足1°。在高宽比恒定的情况下,流量对出射角角度影响较小,出射角变化幅度均在3.5°以内。由此可知,高宽比与出射角的关系更为敏感。

表2 出射角角度测算表Tab.2 Measurement results of angle of projection (°)
窄缝出口断面在不同高宽比下的水舌形态如图3所示。从图3可以看出,高宽比λ从2.25增加至11.25过程中,水舌沿纵向逐渐拉伸,由初始的抛物线状态发展为薄而长的“扫帚状”。高宽比λ自2.25增加到3.75的过程中,水舌扩散程度增加缓慢,在高宽比增至2.815时出射水流出现水帘现象;高宽比λ增至5.625后,水舌形态呈“扫帚状”,此时水舌纵向拉伸充分,同时水翅与水帘清晰可见;高宽比λ达到11.25后,水舌拉伸更加充分,呈现出更完整的“扫帚”形状,水翅与水帘轮廓更加清晰。

3-a λ=2.250 3-b λ=2.815 3-c λ=3.750
2.2 水舌轨迹及挑距
陈忠儒等[16]通过试验,分析各项基本水力参数对挑距的影响,加入流速系数φ2,考虑水舌在空中的自由扩散,选用鼻坎挑角θ1,并提出窄缝增加的出射角θ2的新概念用来表述出射角。结合出射角和收缩比β代入质点抛射体运动公式得出水舌外缘挑距
(1)
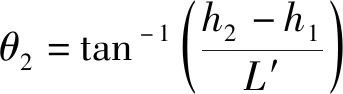
(2)
式中:L1为实测内挑距;φ2为根据试验挑距值推算出的流速系数;φ2取值范围为0.872~0.929,试验取0.92;θ1为鼻坎挑角,其值为10°;θ2为水舌外缘增加的出射角;a2为下游水位到挑坎出口外缘出射点的距离;S为上游水位到顶坎水深中心的距离;h2为窄缝出口断面水深;h1是与之相应缩窄前的水深;L′为水深递增段的距离。
试验发现,当高宽比λ=11.25 时,陈忠儒等[16]公式与实测值偏差较大,此时选用《水力计算手册》中的窄缝挑坎至下游水面的水舌外缘挑距L1计算公式
(3)
式中:v1为水舌外缘出射流速;g为重力加速度,取9.81;同时有
(4)
式中:H0为上游水位至挑坎坎顶的高差;φ选用宁利中[17]公式中流量系数φ1进行计算
(5)
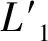
(6)
式中:λ为高宽比,其值为窄缝挑坎出口断面宽度b与窄缝挑坎出口断面高度h的比值。
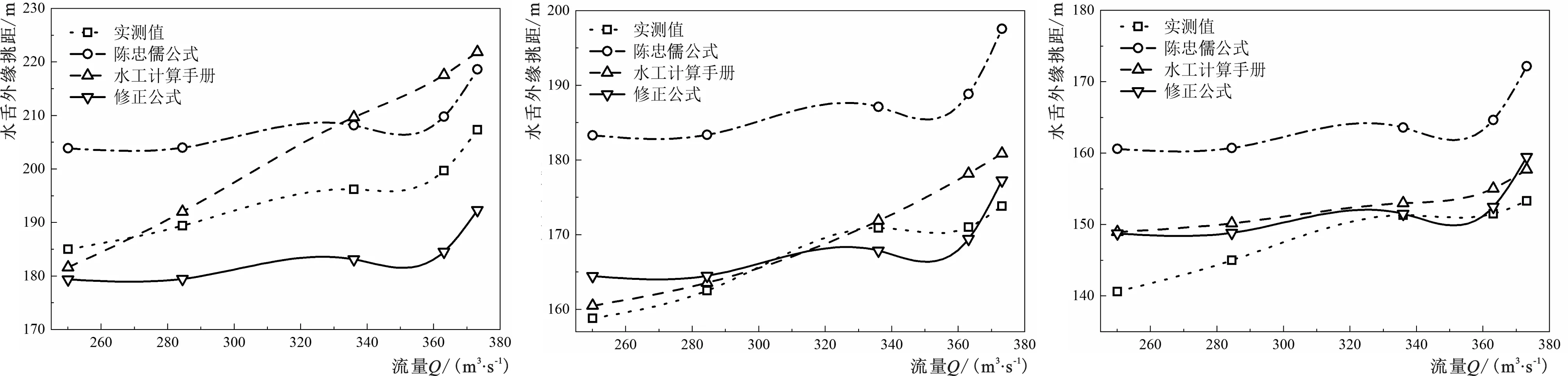
高宽比λ通过控制出口断面宽度b进行调整,将各个工况下的实测值及代入不同高宽比和流量下陈忠儒等[16]提出的挑距公式计算结果、《水力计算手册》[19]进行的修正的公式计算结果分别对比,绘制出图4。
4-a λ=2.250 4-b λ=2.815 4-c λ=3.750
由图4可知,在试验工况中,λ<11.25 区间内,实测结果与陈忠儒等[16]提出的挑距公式计算结果在图像曲线上较为相似,可以通过在陈忠儒等[16]提出的挑距公式基础上进行修正,使计算结果更接近实测值;而在λ≥11.25 的范围时,实测值与《水力计算手册》[19]的公式计算结果更为相近,此时基于《水力计算手册》[19]进行修正的公式计算结果与实测值更接近。综上所述,可以得到基于高宽比下水舌挑距的计算公式,即
(7)
将式(7)代入不同工况,计算结果补充绘制于图4。可知,当高宽比满足2.250≤λ≤3.750时,各公式所得的计算结果与实测值都较为接近;当高宽比5.625≤λ≤11.250时,各公式的挑距计算结果均大于实测值,其中本文提出修正的公式所得结果与实测值最接近,对于预测窄缝挑坎的射流轨迹有一定参考价值。
将式(7)代入各工况得到水舌挑距的计算结果,并将其与实测结果进行整理,结果如图5。由图5可知,断面高宽比对挑距的影响较大,较比而言,流量变化对挑距影响可以忽略。在流量恒定时,高宽比λ的增大加剧了水舌的纵向扩散程度。随着高宽比的增加,水舌内缘挑距减小,同时外缘挑距增加,水舌侧面形态呈薄扇形;当高宽比λ较小时,内外缘挑距相近,水舌侧面呈“一字形”,此时水舌的扩散以横向扩散为主。当流量不变,高宽比在2.815≤λ≤3.750时,外缘挑距随高宽比λ的增加迅速增大;当高宽比λ<2.815及3.750≤λ≤11.250时,外缘挑距随高宽比增加呈缓慢的线性增长。当高宽比λ<3.750时,流量对外缘挑距的影响较小;当高宽比λ>3.750后,流量变化对外缘挑距的影响明显。随高宽比的增加内外缘挑距均减小,当高宽比在3.750≤λ≤5.625及2.250≤λ≤2.815时内缘挑距下降明显,此时内缘挑距值受高宽比影响较大。
将各工况实测值与计算值进行误差分析,绘制水舌外缘挑距实测、计算值对比图(图6)。从图6可以看出,修正公式的计算结果精度较高,实测结果与计算结果较吻合,两者相差小于10%。
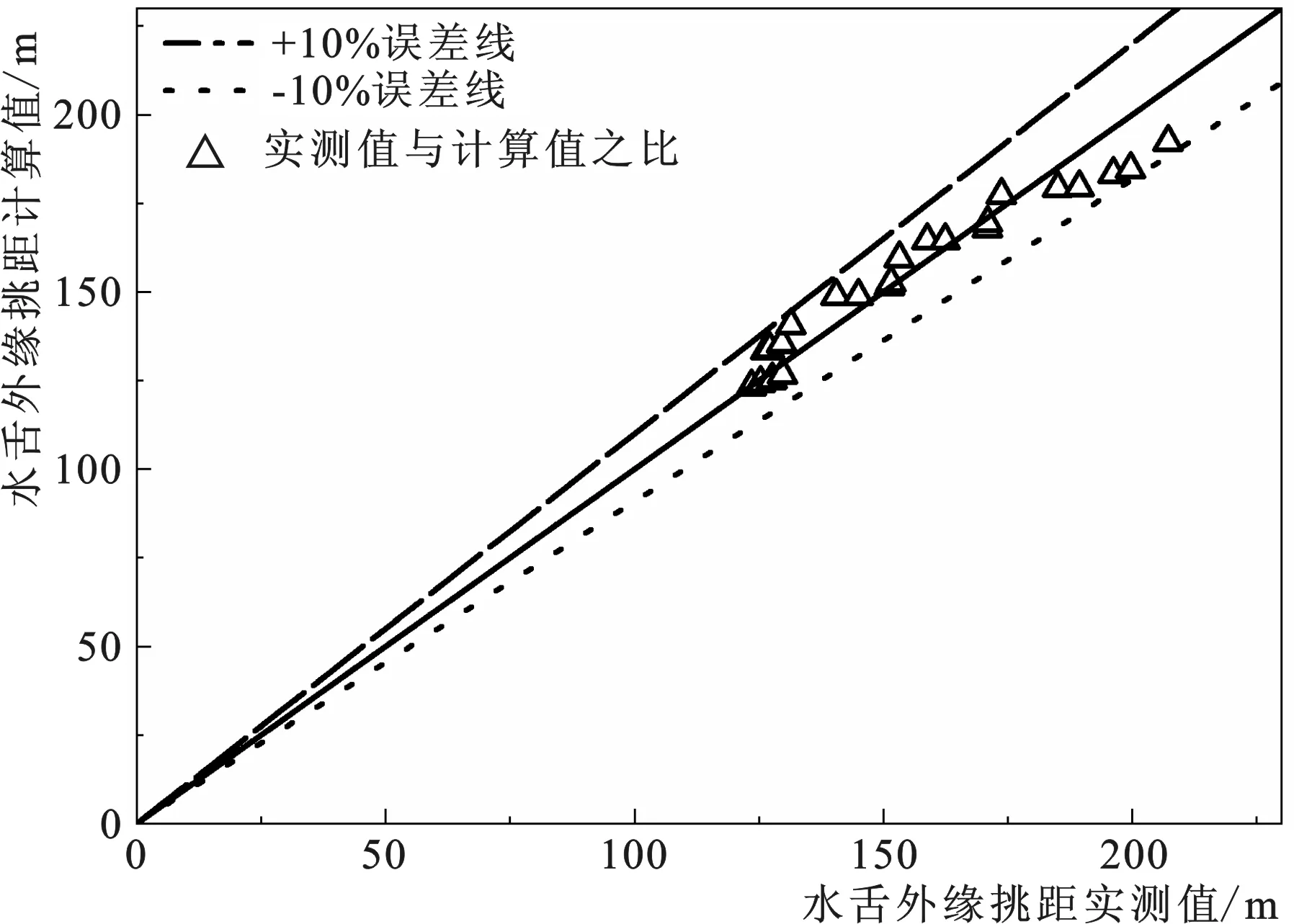
图6 水舌外缘挑距实测、计算值比较图Fig.6 Comparison of measured and calculated values of water tongue outer edge lift distance
3 结论
基于某水电站水工模型试验,研究了不同出口断面高宽比工况下窄缝消能工的挑流轨迹,主要结论如下:
(1)窄缝挑坎射流出射角受高宽比的影响较为显著。主要表现为出射角度随出口断面高宽比的增大而迅速增加,当高宽比λ>5.625后增加幅度尤为明显,较大出射角伴随着更为明显的水翅现象。
(2)讨论了来流流量和出口断面高宽比两个重要水力特性对射流轨迹的影响。较来流流量而言,出口断面高宽比对水舌挑距影响更为显著。当高宽比λ<5.625时,水舌未得到充分的纵向扩散;在高宽比2.250 ≤λ≤11.250时,水舌逐渐纵向拉伸,同时形态逐渐呈“扫帚状”;当高宽比λ达到11.250时,水舌扩散充分,水翅和水帘现象更明显。
(3)基于前人水舌挑距计算公式,利用物理模型试验,参考实测结果,对射流挑距计算公式进行修正,使得修正后的挑距估算公式计算结果与实测值更加吻合。考虑试验测量误差后,修正后的公式计算结果与实测值相差在10%以内。
