解后而三思，直达学生数学思维本质

杨骏

摘 要：数学知识有着纵横交错的联系，解题思路是灵活的，解题方法是多种多样的。所以即使学生能一次把题目做对，解题方法也不一定是最好、最简便的。所以，教师应该让学生在做完题后，进一步学会反思。反思解题中的疏漏，思考解题思路和过程，让学生创造性地去学习，去探索，去总结，从而在更高层次上开发解题智慧，提升思考力。

关键词：小学数学 思维 反思

“数学问题的解决只是完成了学习的一半，更重要的是解题之后的回顾与反思。”解题后的反思是必不可少的重要环节，它能帮助学生总结经验，发现规律，形成技巧，也能触类旁通，有效地提高学习效率。为提高学生的解题能力，教师需提倡并训练学生进行有效的解题反思。

一、思疏漏，确保思维密度

做完题后，为了保证解题的合理性和正确性，我们要积极反思，查漏补缺，归纳总结应注意的方面。如反思题目中隐含条件与答题是否有相抵触的地方；是否还存在其他情形的可能；是不是掉进了命题人设下的陷阱里。以此来提高自己的分析能力，并对自己在答题中出现的错误加以改正。

案例1：长方形裁去一个角，剩余（ ）个角。

错解： 3个角（4个角或5个角）。

正确答案可通过列表表示：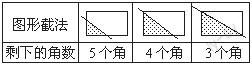

根据图示可知，一个长方形裁去一个角，可出现三种情形。学生往往只会想到一种，教师在引导学生不断思考、寻找准确答案的同时，还要给学生充分的探索时间和空间。

案例2：图1是平行四边形（单位：厘米），一条边上的高是5厘米。它的面积是多少？

错解：6×5=30（平方厘米）

这个解法是不对的。5厘米是平行四边形中的哪个高，学生没有给出正确判断。

其实，图中边长为6厘米的底边，不能以5厘米为高，而仅以边长为4厘米的底边为高，如图2所示。如此，正确答案应为4×5=20（平方厘米）。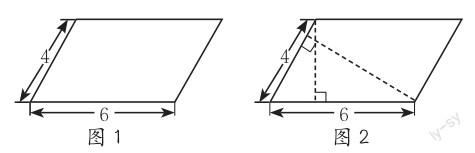

上面的例子告诉我们，要做到解题正确，审题、分析都很重要，还要有条理地思考。小学生的生理、心理特征往往会导致思考问题比较片面，就容易犯上述的错误。作为教师，要培养学生解题后反思的能力，及时“回头看”，对解题的结果做一个总结。

二、思算法，提升思维广度

（一）思方法，找规律

很多题目的解题思路是一样的，学生通过解题后的反思总结出解决这类题目的方法，以后再碰到这一类的题目，就知道从哪个方面思考才不至于走彎路，解题的思路也能更清晰明了。学生领会了解题方法的实质，运用总结出的方法，就能解决同类型的习题，通过归纳整理，数学学习就变得更简单了。

因此，我们要培养学生阅读、分析题目的能力，寻找数学的本质问题，寻找规律，把一个复杂的问题分解成若干简单的问题。解题后再进行回顾、梳理，把同类型的习题进行对比，找到共性的方法，然后再升华、提炼成解题方法，最后运用到以后的解题中去。教师引导学生养成这样的习惯，长此以往，其数学基本功终将形成。例如，在基本的四则运算中，有些虽不是法则，但也有规律可循。

案例3：仔细观察一下，下面的减法有什么特点？它们的差有什么规律？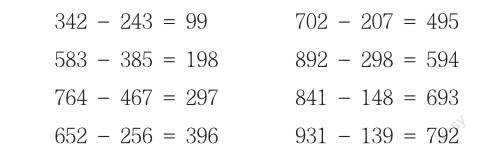

分析与解答：

（1）通过观察，你发现上述算式中有怎样的相同点呢？

（2）上面各题的差都是几的倍数？分别是这个数的几倍？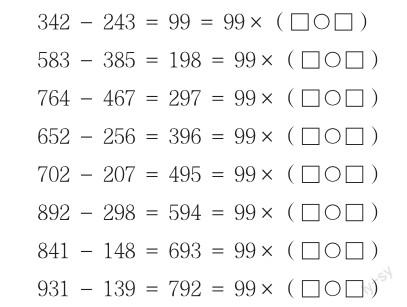

（3）上述题目中，前后算式有什么关联吗？

（二）思一题多解

新课标指出，要注重数学知识和方法的层次性和多样性，采取螺旋式的方式，适当体现选择性。因此，在数学解题的过程中，教师要鼓励学生从不同的角度解题，衍生出更多的解题方法，提升学生数学学习的思维广度和思辨能力。此外，还要培养学生在不同的解题方法中寻找最优解的能力，感悟数的运算的一致性。

我们由上述算式看出，尽管答案有很多种，从不同的角度可以填写不同的数使算式成立，但都有其一致的基本方法，就是要先假设等式的结果，再根据不同的运算规律填写。笔者认为，利用倒数的性质和0的特征可以快速答题，但是假设法和一致性两种方法可以拓展学生思维的广度，教师在讲解时要抓住其本质特征，引导学生寻找多种方法。

教学中适当的一题多解，能激发学生的探究欲望，加深学生对所学知识的理解，训练学生熟练运用数学思想和方法，拓展思维的广度，使学生的思维素质得到培养，创造性思维得到发展。

班里学生的学习能力各不相同，教师要针对学生的这一特点，设计适当的开放性练习，使不同层次的学生都能找到适合自己的方法。在不同层次的解题思路中，教师通过点拨，对学生的数学思维进行优化、训练，使其能够选择合理、简明的运算策略进行解题，形成规范的思维品质。

（三）思算法多样化

新课标指出：“由于学生生活背景和思考角度的不同，所使用的方法必然是多样的，教师应尊重学生的想法，鼓励学生独立思考，提倡计算方法的多样化。”“提倡算法多样化”是数学课程标准的重要理念之一，其实质是尊重学生的个性发展，提倡个性化学习，支持和鼓励学生在数学学习中用自己喜欢的、熟悉的、擅长的思维方式解决问题。

教师在课堂上要营造宽松的氛围，给予学生更多思考和表达的机会，鼓励学生在数学问题面前勇于尝试，从多角度解决问题，并且能够用自己的方法表达出来。同时，算法多样化要区别于一题多解，比一题多解的要求低些。只要方法合理，学生表达清楚，教師就应该予以肯定和鼓励，这是一种基于学生不同认知水平和个性的体现。

但应注意的是，在课堂教学中，教师要避免为了多样化而多样化，避免低级的多样化，引导学生过滤无意义的方法。方法多样化应该是基于发展学生思维水平的要求之上的，基于不同的认知水平，一些学生找不到富有个性的方法，这时也不要强求，要带领这部分学生学习别人的方法。

三、思问题，挖掘思维深度

在数学教学中，如果教师还是停留在因“解”而“解”的阶段，那么对于数学深度的挖掘是不够的。教师对数学习题的讲解不在多而贵在精，在讲解一题时要有同类型、不同层次习题的储备，解题后引导学生反思，深挖此类题的解法，追问同类型习题还可以往什么方向发展。比如把条件和题目修改一下，变成另外一个题目，同时把其他准备好的习题拿出来让学生去思考，把更深的、更难的题目用已经总结好的方法去解决，把学生的思维层次挖得深一点儿，做到举一反三。

综上所述，我们要培养学生解后而三思的良好品质，要思疏漏、思算法、思问题，在思维品质的密度、广度、深度上下功夫，培养学生的核心素养，使其会用数学的眼光观察现实世界，用数学的思维思考现实世界，用数学的语言表达现实世界。

参考文献

[1]斯苗儿.小学数学教学案例专题研究[M].杭州：浙江大学出版社，2005.

[2]张玺恩.中国著名特级教师教学思想录（小学数学卷）[M].南京：江苏教育出版社，1996.

[3]连林翟.小学数学优秀题解析[M].北京：北京教育出版社，1990.

[4]杨庆余.小学数学课程与数学[M].北京：高等教育出版社，2004.

[5]郑毓信，肖柏荣，熊萍.数学思维与数学方法论[M].成都：四川教育出版社，2005.

[6]陶兴模.注重培养学生解题后反思的习惯[J].中学数学月刊，2002（3）.

[7]郑建伟.谈数学的反思式学习，培养学生的创新能力[J].数学教学研究，2011（9）.

[8]吴卫东.对算法多样化的理性思考[J].教学月刊（小学版），2003（2）.