基于非遗传进化算法的四边形海上风电场设计

傅晓军，金超，王晓东

（国电象山海上风电有限公司，宁波 315042）

引言

海上风电技术正成为可再生能源发电的一种现实选择[1]。尽管在世界电力市场中的作用越来越大，但是这只占全球能源产量的0.3 %[2]。已有的实践结果证明，海上风电场项目成为一项风险越来越小的投资，其对潜在开发商更有吸引力[3]。然而就停滞状态下的每兆瓦成本而言，这仍然是最昂贵的技术之一。因此在考虑实现海上风电场之前，有必要进行彻底的盈利能力分析[4]。四边形风电场是一种海上风电场建设中较常用到的一种设计[5]。在实际工程应用中，有学者提出了一种海上风电场的风电机组排布平行四边形推进方法。在平行四边形风电场的建设中，根据风电场边界确定网格区域的范围，在该区域内以平行四边形进行划分，可以得到若干可选机位点，从而确定风电场的布局。在理论层面上可以通过枚举所有平行四边形的排布方案，然后得到风电场最大发电量的优化方案。白光谱等人在研究中使用基于平行四边形形状解的搜索算法来确定涡轮机之间的距离、平行四边形的方向和角度，以最大限度地提高能量生产[6]。然而在实际情况下还必须找到涡轮机之间的确切位置、方向、倾斜度和最佳分离距离（考虑到或多或少较宽的进入区域）。那么需要增加可能性的数量直至能够处理这些变量的有效程度。在这些要求下，传统的遗传算法（genetic algorithm，GA）是不合适的，该算法无法同时处理可能性数量较多的多种连续变量。因此在此次研究中详细介绍了这项工作提出了一种非遗传进化算法（non-genetic evolutionary algorithm，NGEA）， 该算法使用八个连续变量，涉及中心坐标、行数、每行涡轮机数量、行之间和一行涡轮机之间的距离、行方向和平行四边形角，可以用于完整的经济、水深和风力数据的分析。对结果的检查表明，使用实数运算的非遗传进化算法来确定定义平行四边形海上风电场的决策变量。在更好的场地开发下，使用非遗传进化算法也可能实现其他常规布局。

1 海上风电场设计

1.1 海上风电场成本控制研究

作为可再生能源发电的一种现实选择，海上风电场在世界电力市场中的作用越来越大。在已有的海上风电场实践中获得的知识，以及海上风电场项目开发中突发事件的来源和严重程度来看，海上风电场项目中的风险程度更低。这使得海上风电场项目成为一项风险越来越小的投资，这对潜在开发商更有吸引力。然而，就停滞状态下的每兆瓦成本而言，这仍然是最昂贵的技术之一。因此在考虑实现海上风电场之前，有必要进行彻底的盈利能力分析。在该分析中，必须考虑现场条件，以细化投资成本，并推断出涡轮机的最佳布置，从而最大限度地提高电能产量并将投资降至最低。

王栋杰等人在研究中解释了不同的经济函数，以评估未来投资的盈利能力[7]。其中，平准化能源成本（LCOE）、内部收益率（IRR）、折现回收期、投资回报率或效益成本比被用作衡量运营风险和投资质量的指标[8]。另一方面，还需要将最大投资限制在一定值，但是净现值（NPV）适合在OWF 布局的互斥选项之间进行选择，因此应在优化算法中用作目标函数。为了将最大投资限制在一定的价值，还需要进一步优化算法。由于NPV 是给定时间段内公司现金流入的现值和现金流出的现值之间的差值，因此可以表示为公式（1）。

式中：

T—实用寿命；

AEP—年净能源产量（扣除尾流干扰和电力基础设施中的总损失后）；

pkWh和△pkWh—能源价格及其年增量；

OPEX 和△OPEX—运营和维护成本及其增量；

CAPEX—总投资成本；

Dec—扣除工厂剩余价格后的按时退役成本；

r—贴现率，可以由名义利率ri和通货膨胀inf 得出，见公式（2）。

公式（2）中年金系数α 的定义见公式（3）。

LCOE 可以表示为公式（4）。

在一些研究工作中，假设贴现率与加权平均资本成本（weighted average cost of capital，WACC）相似，并略高以调整风险[9,10]。在此次研究中，设置了ri=9.4 %和inf=1.5 %，由此可以得出r=7.78 %。

对于每个风向φ 和每个风速u 来说，风力发电厂每年产生的能量可以通过将Nt台涡轮机中每一台产生的能量Ek加在一起来获得。因此在一年的时间中（Ty=8 766 h），AEP 可以表示为公式（5）。

式中：

ucut-in—切入速度；

ucut-out—切出速度；

Pc—由涡轮机功率曲线给定的特定风速下的电能；

fr（φ，u）—速度v 和风向φ 下的概率密度。

在这个表达式中，阵列的涡轮机k 产生的功率取决于到达第k 个涡轮机的气流的有效速度。由于尾流效应，该有效速度小于自由流空气速度u。在风电场优化问题中，有不同的方法来估计尾流引起的风速不足。在一已有的研究中，研究人员使用的最简单、最流行的尾流模型是PARK 模型[11]。它首先由Jensen 和Katic 提出，从尾流直径（Dw）等于逆风涡轮机的转子直径（D）开始。假设逆风风力涡轮机后面的尾流扩展与涡轮机之间在风向上的距离投影成线性，那么Dw的计算见公式（6）。

式中：

比例因子是尾流衰减常数（kw），其可以表示为塔毂高度（h）和表面粗糙度长度（z0）的函数，见公式（7）。

对于第一次评估，使用了0.052 5 的值，从z0=0.005（对于海上场地通常如此）和h=70 获得。然而，海上风电场荷斯韦夫I（Horns Rev I，HR-I）布局的区域效率为91.5 %，高于已有研究中观察到的89 %[12]。事实上，为了考虑到湍流强度（turbulence intensity，TI）的影响[13]，同时稳定性越低，kw就越高，那么从公式（7）中获得的值应该进行调整。当湍流强度不可用时，研究人员对kw进行拟合，以便从尾流损失模型中获得的结果与观测值相匹配[14]。其中海上场地中的kw=0.04。根据动量理论，尾流膨胀会产生风速损失δ，该损失取决于逆风推力系数Ct，见公式（8）。

式中：

v—下游位置的尾流速度；

v∞—未扰动风速。

在涡轮机受到多个逆风涡轮机扰动的情况下，必须增加尾流影响的研究，以获得有效风速的不足。在已有的文献中已经提出了不同的聚合方法[15]，其中优选的方法是平方根，见公式（9）。

作为由于来自N个上游涡轮机的单个尾流而导致的下游位置处的不足的均方根，其能获得任何涡轮机处的总风速不足。在与海上风电场建设的相关工作中，这种组合方法是与观测到的功率数据表现出最佳匹配的方法[16]。考虑顺风涡轮机仅部分受到尾流影响的情况，可以改进公式（9）中的计算方法，改进后的方法见公式（10）。

式中：

—影响顺风涡轮机的逆风涡轮机i部分尾流的表面。

1.2 海上风电场规划方法中的非遗传进化算法研究

通过利用考虑平行四边形布局解决方案（具有均匀分布的涡轮机）所带来的复杂性降低，本工作引入了一个完整的风电场优化问题，该风电场优化问题搜索海上风电场的位置、大小和布局的最佳值，以最大限度地提高项目盈利能力。传统的遗传算法无法实现一个完整的搜索，因此只有放弃使用遗传算法独立定位每个涡轮机的想法。相反，这项工作提出了一种非遗传进化算法，该算法使用八个连续变量，涉及中心坐标、行数、每行涡轮机数量、行之间和一行涡轮机之间的距离、行方向和平行四边形角。它与典型的遗传算法具有基本相同的结构，但调整其交叉和变异算子以处理连续变量。与现有的基于遗传算法的工作相比，所提出的方法可以在不影响计算时间的情况下在广阔的特许区域内进行搜索。

风电场优化问题的目的是获得特许区内海上风电场的最佳位置和布局，从而优化某个目标函数[17,18]。在本工作中，该目标函数就是平准化能源成本（levelized cost of energy，LCOE）。该方法并不寻求独立定位每个涡轮机，这会导致布局不规则。相反，在这项工作中，每一代的个体都是平行四边形的海上风电场，其中涡轮机均匀分布。LCOE 目标函数由以下8 元组定义可得：中心的坐标X 和Y；nr表示行数；ntr表示每排涡轮机数量；对于行之间的距离而言，其单位为直径（dr）；对于一排涡轮机之间的距离而言，其单位为直径（dtr）；阵列的方向在相对于北方的位置，其单位为度，方向为CW（θ）；平行四边形角；对于矩形（φ），其值等于90 °。图1为这些决策变量的表示方法。

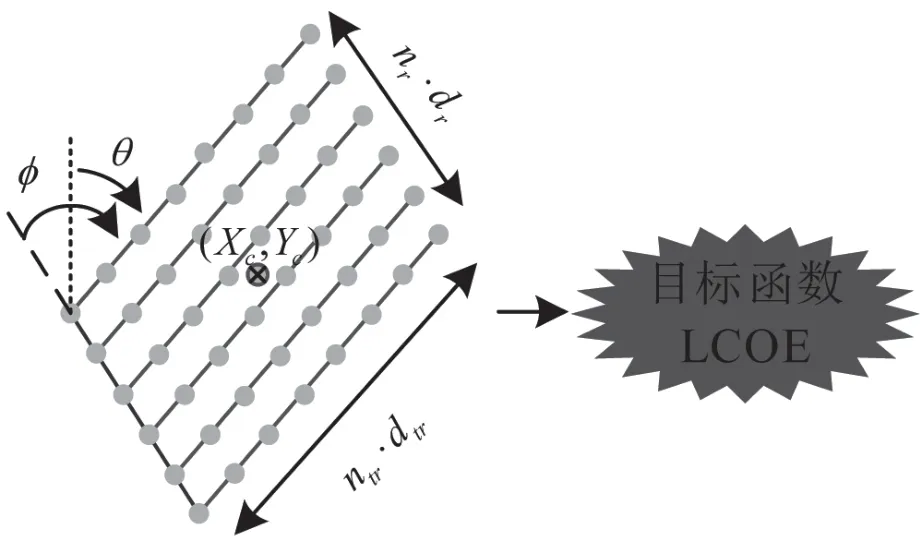
图1 决策变量的表示方法

研究中所提出的非遗传进化算法（NGEA）必须获得这八个决策变量，以定义最小化LCOE 的海上风电场。其中，六个是实数，两个（行数和列数）是离散值。这两个变量不会增加额外的复杂性，因为它们可以很容易地转换为连续值。因此，该算法可以被认为具有连续值。

通常，以下限制适用于所提出的算法：①所有的涡轮机都是相同的类型，转子处于相同的高度。因此，它仅适用于海上风电场地。②涡轮机均匀分布，形成平行四边形的海上风电场，且所有行都有相同数量的涡轮机。③电缆尺寸和变电站位置得到了优化，但没有优化涡轮机之间的连接。即，一排的所有涡轮机必须按照HR-I[12]中的径向电缆布置从最后一台连接到第一台。④从海上变电站到海岸过渡的高压电缆轨迹没有得到优化。

对于这一特定的研究案例，以下限制适用于所提出的方法：①最多允许80 台涡轮机。②涡轮机位置仅限于适当位置的浅水区。本研究中的搜索区域仅限于缩小的空间，但通常情况下，搜索区域可以扩大到数千平方公里，而不会影响计算时间。③对于第一个优化，行中涡轮机之间的距离dtr和行之间的距离dr是固定的，并且等于7D。对于第二个优化dr，dtr∈[5D，20D]。

在大多数研究风电场优化问题中，研究人员所使用的传统遗传算法不适合处理连续变量[19]。从这个意义上说，用实数运算的NGEA 已经被编程，以确定定义最佳平行四边形海上风电场的八个决策变量。它的结构基本上与典型的遗传算法相同，尽管它调整了交叉和变异算子来处理连续变量。该算法按照图2 的操作顺序进行编程，其中交叉一词被重组取代，这在NGEA 中通常是首选的，以设计结合父母基因型产生新后代的算子。其操作规范为：人口规模，150 人；最大世代数，250；重复完成，40 次；初始种群中的个体，100 个；交叉概率，80 %；突变概率为12 %。图2 为优化方法的操作步骤。

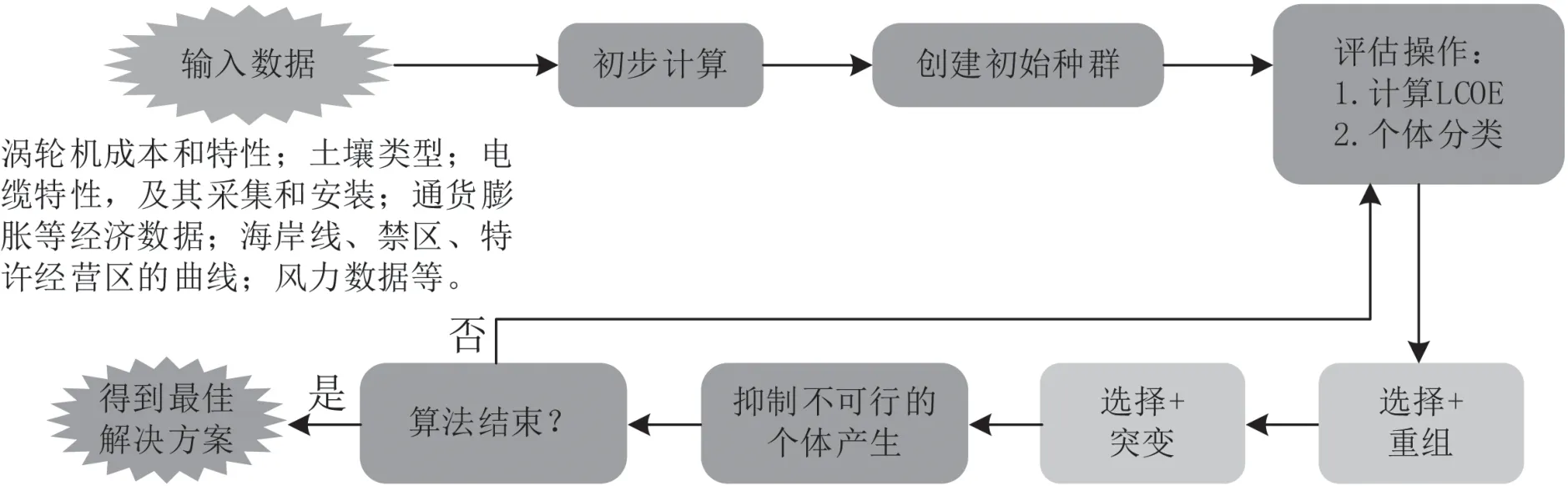
图2 优化方法的操作步骤

研究表明在大多数风电场优化问题的研究中，研究人员使用的遗传算法不适合处理连续变量[20]。从这个意义上讲，对使用实数值运行的NGEA 进行编程，可以确定最佳平行四边形海上风电场八个决策变量的定义，从而进行连续变量的计算，最终实现在不影响计算时间的情况下在广阔的特许区域内进行搜索。

2 基于非遗传进化算法的海上风电场实验结果

本次研究中所提出的方法已经在流行的HR-I 网站上进行了测试。该海上风电场已在许多研究工作中用作测试台，以证明所提出的优化算法的有效性，或作为评估尾流损失的方法。对于第一个目标，大多数测试算法的输出是涡轮机沿特许区不规则分布的布局，因此没有产生关于涡轮机排列的优先方向的有用信息。

因此第1.2 节中所示的算法被执行了十次，以确定HR-I 所在地风电场的最佳布局。前五次优化搜索的约束条件是将涡轮机限制在浅水区域（＜10 m），不包括提取区域和靠近海岸的敏感区域。当解决方案被限制在一个大的特许区域时，在图3 中展示了获得的最佳个体参数。图3（a）表示每一代最佳个体的中心位置。图3（b）表示行的方向角和平行四边形的角度。图3（c）表示一排涡轮机之间以及排与排之间的间隔。十个优化搜索的结果用不同的颜色表示。从图3（a）中可以看出，海上风电场中心的位置没有分散。从图3（b）中可以看出方向和倾斜度也是相当恒定的。同时从图3（c）中可以看出具有很长距离的解决方案是优选的，因为它们可以减少尾流效应（涡轮机之间的最大距离限制为20D）。

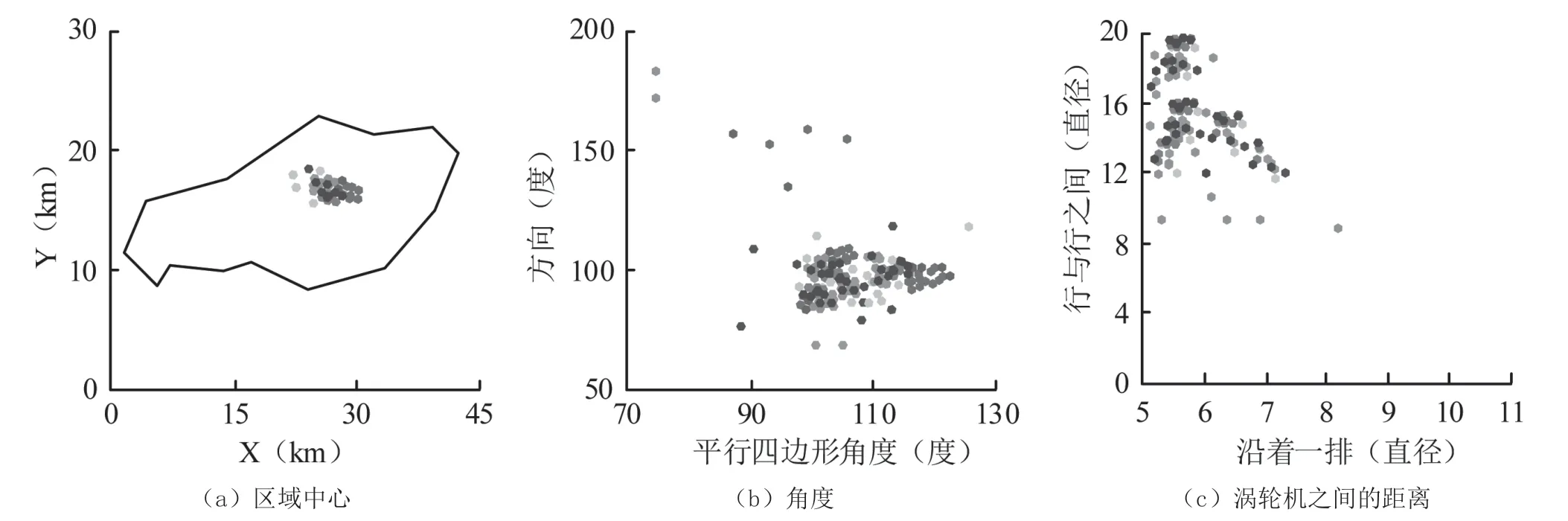
图3 最佳个体的参数

然而，特许经营区通常被缩小到更小的区域，开发商被迫减少涡轮机之间的间距。根据这一问题，将距离固定为7D，进行了一组新的五次搜索，结果如图4 所示。图4（a）表示每一代最佳个体的中心位置。图4（b）表示行的方向角和平行四边形的角度。图4（c）表示每排具有一定数量涡轮机的个体的LCOE 平均值和发生次数。十个优化搜索的结果用不同的颜色表示。同样，该中心位于特许区的中部。方向值在（55～95）°之间变化，而平行四边形角度在（85～95）°之间。图4（c）显示了最频繁的布局和每个布局的LCOE 平均值。16×5 的布局是最常见的布局，目标函数LCOE 的值较低（即最佳）。同时存在一些10×8、11×7 和13×6 的解决方案，最后两个解决方案包括比特许权允许的更少的涡轮机。如果选择NPV作为目标函数，这些解决方案在搜索过程结束时几乎不会出现。

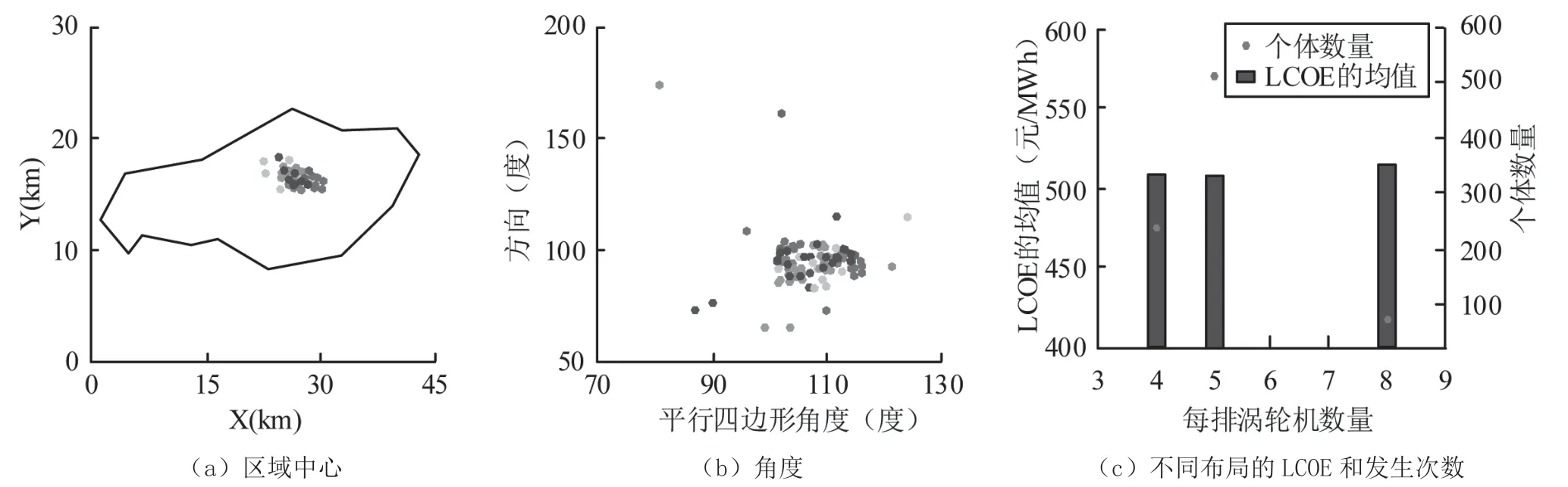
图4 距离固定后的最佳个体参数

每一代适应度的演变如图5 所示，表明最佳适应度通常在不到100 代的时间内达到。研究中还给出了计算时间，对于涡轮机之间的长距离，每次优化搜索的平均时间为2 400 s。而对于正常的分离，每次优化搜索的平均时间为2 800 s。

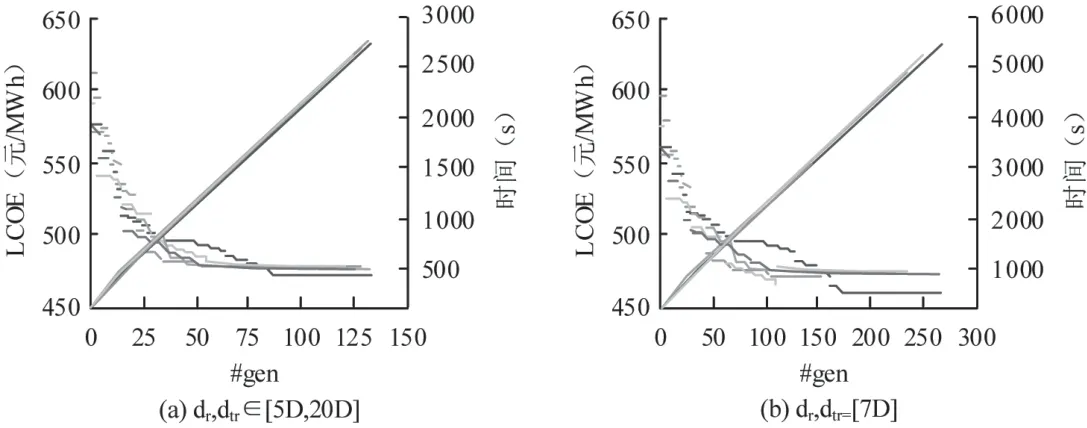
图5 个体适应度的演变

图6 显示了行和列的最频繁方向的演变。每一代最佳个体的行和列的首选方向。图6（a）表示行和列之间没有分隔限制时的值。图6（b）表示施加了7D 的分隔。五个优化搜索的结果用不同的颜色表示。柱方向是通过减去方向和倾斜度来获得的。优选的对齐方向约为60 °和150 °，试图能避开能量不足的风向。

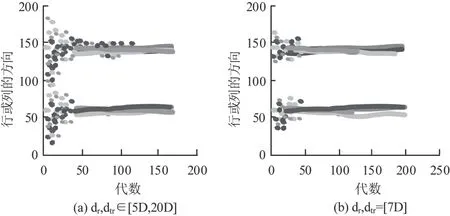
图6 行和列中最频繁方向的演变

最后对基于遗传算法的搜索方法与本文中的搜索方法进行了最终决策变量的比较，电气损失分别为8.53 GWh 和9.88 GWh，尾流损失分别为76.81 GWh和40.68 GWh。尽管优化后的电气损失相较优化前增加15.83 %，但尾流损失减少47.04 %，极大减少了整体能耗。在运营成本方面，从优化前的142.4 元/GWh 增加到149.7 元/GWh，但度电成本从61.26 元/GWh 降低到59.34 元/GWh，整体内部收益率提高0.83 %，风电场净现值从7.293 亿元增加到8.609 亿元，见图7。

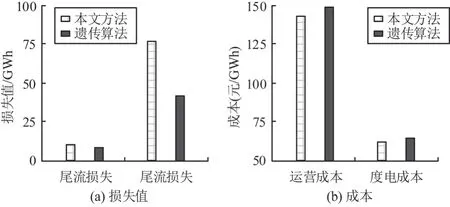
图7 方法对比

本次实验中分析了平行四边形海上风电场的方位和倾斜度的最佳值，并将结果与实际布局进行了比较。使用均匀分布的涡轮机的另一个优点是，定义最佳方向、方位和倾斜度的两个变量为设计者提供了关于优选方向的信息，以使涡轮机与未来用于选择对开发商最具吸引力的特许区域的目标对准。如果特许区域足够大，尽管要安装的涡轮机的数量或功率有限，但该算法也可以通过完全定义其位置、距离、方向、倾斜度和布局（按行和列分布）来找到最佳解决方案。作为一个相对的缺点，涡轮机位置不能自由地位于海上风电场区域中，并且被迫均匀分布，从而将可能的候选频谱减少到最佳。然而，在有和没有均匀分布涡轮机限制的情况下进行的优化对比结果显示，由此产生的净能量产出差异非常小，其差值小于1 %。

3 结论

该研究对HR-I 海上风电场相关的尾流效应所遇到的能量损失进行了研究，并考虑了一种影响项目盈利的遗传算法对项目涡轮机布局进行优化，使其具有一致性。在研究过程中，考虑了海上风电场经济评估的相关因素，定义了形状类似平行四边形的最优海上风电场的涡轮机分布位置、尺寸和配置。鉴于算法应该找到涡轮机之前的确切位置、方向、倾斜度和最佳分离距离，对传统的遗传算法模型进行优化，选择实数运算的NGEA来确定海上风电场的决策变量。研究结果显示，10 个优化结果的区域中心横轴范围为（15～30）km，纵轴范围为（10～20）km，平行四边形角度为（100～120）°，方向角度为（85～105）°，每行涡轮机之间的距离为（9～20）m，每列涡轮机之间的距离为（5～8）m。涡轮机距离优化前的平均搜索时间为2 800 s，而优化后的搜索时间为2 400 s，效率提升14.29 %。此外，具有特许经营区倾向的风电场对潜在开发商更具有吸引力，风电场净现值能够提升18.04 %。研究的不足之处在于优化后风电场整体内部收益率提高不足1 %，以后的研究应向提升整体内部收益率努力。