基于均匀试验的MJS加固江堤参数敏感性分析

2023-09-06蒙邹蕾王翀霄

水道港口 2023年3期

孙阳,蒙邹蕾,王翀霄,姚森

(1.河海大学港口海岸与近海工程学院,南京 210098;2.南通河海大学海洋与近海工程研究院,南通 223003;3.中铁大桥局集团有限公司,武汉 430000)

MJS工法桩(Metro Jet System)是在高压旋喷桩的基础上创新形成的工艺,可实现360°全方位成桩,与土体凝结成强度较高的柱形桩体,对周围环境扰动极小且能够适应水下施工,因此得到了迅速推广[1]。在数值模拟方面,LUO等[2]、XIONG等[3]、陈仁朋等[4]、王岩[5]、周朋[6]均对MJS工法水平桩加固隧道周围土体进行了研究,研究表明MJS工法桩能够有效提高地基承载力,降低了盾构开挖过程中对既有隧道和周围地层的影响,并且具有良好的抗震性能。宋玉芹等[7]以上海越江隧道穿越高架桩基为例,采用数值模拟的方法,探讨了MJS桩不同桩径对桩基和地表沉降的影响。赵云建[8]采用FLAC3D有限元软件模拟了盾构下穿高速铁路过程中,不同注浆置换率的水平旋喷桩加固对地表沉降的影响。现有研究只能考虑单一因素的影响,未开展MJS桩加固效果的多参数关联性分析。研究各因素间的交互效应、敏感程度及关联机制,常见的试验设计方法有正交试验、中心组合试验(CCD)、Box-Behnken试验(BBD)和均匀试验。对于多因素共同作用的复杂问题,变形机理模糊、影响因素复杂,均匀试验法是解决该类问题的有效手段,对于指导工程设计和施工具有重要的工程应用价值及理论意义。

在江堤稳定性计算方面,数值分析方法包括有限元单元法[9]、边界单元法[10]和离散单元法[11]。其中,有限单元法被大多数数值分析软件所采用,有限元软件中计算江堤安全系数的方法为强度折减法[12]。梁一星[13]和赵翔[14]基于流固耦合有限元模型,采用强度折减法计算江堤安全系数,与经典毕肖普法计算结果对比,证明了有限元强度折减法应用于江堤稳定性分析是可行的。随着计算技术的发展,人们也更倾向于使用这一方法计算江堤稳定性问题,尤其用于复杂形态和涉及复杂施工的江堤工程问题。

本文以南京市建宁西路过江通道大直径盾构切削江堤抗滑桩实际工程为例,基于三维有限元模型,考察盾尾注浆压力、支护压力、MJS加固长度、加固宽度和加固高度等参数在合理范围内变化时江堤的安全系数变化和最大位移变化。运用均匀性原理对影响江堤加固效果的多参数关联机制进行定量评价,以确定各影响因素之间的主次关系,为盾构穿越堤防加固设计方案的进一步优化提供决策依据。

1 工程概述

南京市建宁西路过江通道一期工程位于长江大桥和扬子江隧道之间,建宁西路过江通道拟采用两台泥水盾构机分别施工两条隧道(图1),由北岸工作井向江南始发掘进,隧道外径为14.5 m,内径为13.3 m,管片厚度0.6 m,两隧道净距为17～18 m。南岸堤防处被切筋混凝土抗滑桩桩径900 mm,桩间距1.5 m。盾构施工前采用MJS竖直桩对长江南岸堤防和岸坡加固。在区域③内对堤身进行整体加固。

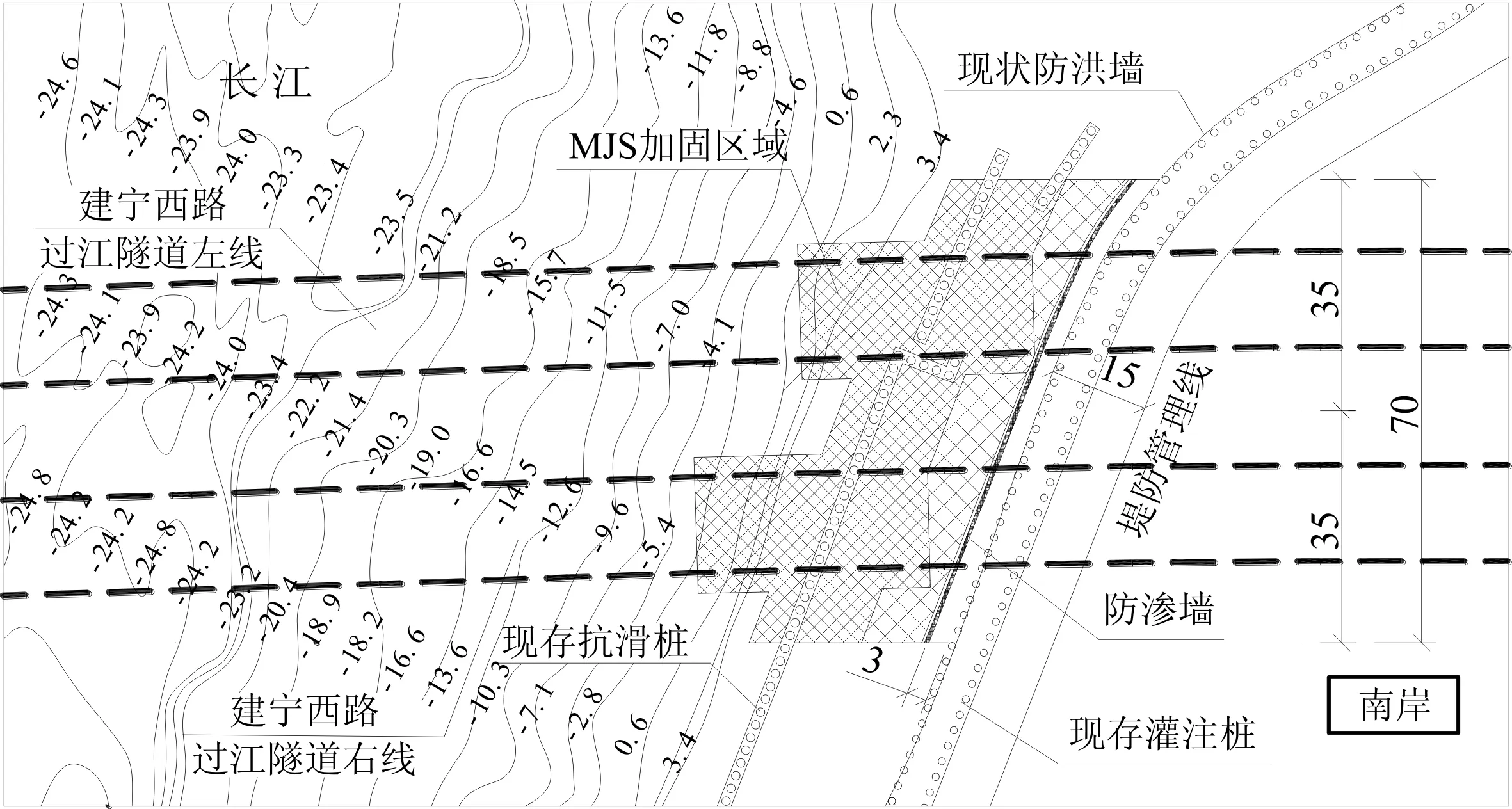
图1 堤防岸坡加固平面图(单位：m)Fig.1 Plan of reinforcement of the bank slope

2 计算方法及参数选取

2.1 土体参数选取

项目区盾构段洞身深度内以流塑状淤泥质粉质黏土及饱和粉细砂、砾砂、圆砾、泥岩、角砾岩、泥质粉砂岩、白云岩为主。堤身为③4淤泥质粉质黏土呈流塑状、易蠕动的松软结构;②2层粉砂层呈潮湿的松散结构,为液化土层,均属于不良工程地质层。具体的土体参数见表1。

表1 土体参数Tab.1 Parameters of soil and rock

2.2 盾构施工参数

本文研究内容涉及的盾构施工参数主要包括支护压力和注浆压力。支护压力对开挖面的稳定性的影响至关重要,保证开挖面的稳定是控制表面沉降的关键,在开挖面支护压力欠压状态下推进,会造成开挖面前方土体大范围沉降;在开挖面支护压力超压状态下顶进,会引起开挖面前方土体隆起,因而支护压力需要单独计算,避免以沉降数值为因变量进行相关分析时误认为越大的支护压力越好。注浆压力沿盾尾注浆环向分布,其对隧道上方土体沉降影响较大,且有明确的取值范围。因此,将影响可能显著的注浆压力作为试验因素之一展开均匀试验。

2.3 MJS加固参数选取

为了优化MJS的加固效果,考虑注浆压力、加固长度L、宽度B以及高度h作为试验因素,如图2所示,均匀设计试验影响因素的取值范围如表2所示。均匀设计法的主要思想是将试验点均匀地布散在平面格子上,并且保证每个水平每个因子的试验机会都是相等的。均匀试验可通过均匀表Ul(lm)进行试验设计,本试验选取U15(157)均匀设计表[15],通过使用表选取1、2、4、6列完成试验设计,如表3所示。

表2 江堤稳定性影响因素的取值范围Tab.2 Value range of factors affecting slope stability

2-a 俯视图 2-b 右视图图2 MJS加固参数示意图Fig.2 MJS reinforcement parameters

3 三维数值模拟

3.1 模型建立和计算结果

本文采用 PLAXIS软件进行完全流固耦合计算,模型尺寸为200 m×150 m×80 m(盾构掘进方向×垂直盾构方向×高度),土体本构模型为摩尔库伦弹塑性模型[16-17],基本参数采用表1中的数值。盾构机外环面以及抗滑桩采用板单元模拟,最终衬砌采用实体单元模拟,堤身旋喷灌浆加固区域采用实体单元模拟。假设抗滑桩单排直线布设,根据等效原则简化为一定厚度的抗滑桩墙。MJS加固区根据等效刚度原则,通过计算高压旋喷桩对原有土体的置换率,从而得到整个加固区内复合加固土的参数。板单元设置相应的正向界面或负向界面,模拟结构与土体或是与其他实体单元的相互作用。

数值模拟中14.5 m大直径泥水盾构的管片长度为2 m,盾构机长度为7环管片长度(14 m)。模拟计算时以一个管片长度为几何模型片段,将隧道划分为若干个2 m长的片段,盾构机最后一个环宽为尾部空隙注浆段,盾构每次向前推进2 m,同时安装完成盾尾后一个环宽的最终衬砌,三维模型图如图3所示。

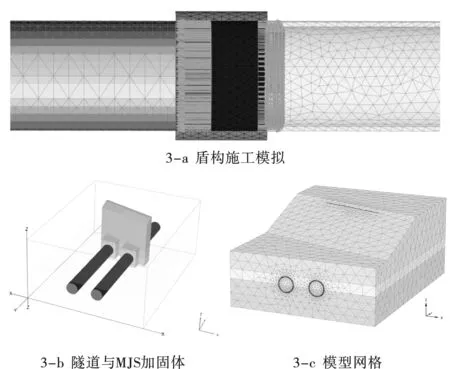
图3 三维计算模型Fig.3 3D calculation model

江堤岸坡稳定的安全系数的计算采用有限元强度折减法,该方法定义了一个强度折减系数FS,即江堤内岩土体在外部不变的荷载下所提供的抗剪强度最大值τf与在江堤内由外荷载产生的实际剪应力τ的比值

(1)

强度折减法通过对土体的抗剪强度指标c和φ进行不断折减,最终得到江堤失稳时的c′和φ′,江堤失稳时的抗剪强度指标与原抗剪强度指标的比值即为安全系数。

(2)

(3)

3.2 数值模拟计算结果

将试验点代入三维模型中,如图4所示,随着盾构推进,沉降由盾构面逐渐传递至坡面,由于抗滑桩和MJS加固区域的存在,盾构产生的扰动难以传递至坡顶,各试验所得的最大沉降位置均位于坡面距堤脚约1/3处。

图4 隧道轴线纵剖面沉降云图Fig.4 Longitudinal section of tunnel axis

如图5所示,由于抗滑桩与MJS加固区域的存在,危险滑动面起始于抗滑桩下方,在滑动面顶部1 m范围内,其方向与抗滑桩方向一致,随后逐渐变化为圆弧面,最后终止于坡脚。

图5 江堤位移云图Fig.5 Displacement cloud of river embankment

由于各试验计算所得的最大沉降位置与危险滑弧的形态基本一致,故针对最大沉降量和安全系数展开各参数敏感性分析。计算得到盾构掘进过程中江堤表面最大沉降和加固后的安全系数,如表4所示。

表4 均匀设计试验计算结果UzmaxTab.4 Uniform design test calculation results of Uzmax

3.2 MJS加固参数敏感性分析

以注浆压力、加固长度L、宽度B以及高度h为自变量,江堤表面最大沉降、江堤稳定性安全系数为因变量,采用Pearson相关系数r对自变量与因变量的线性相关程度进行分析,并进一步计算显著性系数sig.寻找影响水平较高的变量[18]。

3.2.1 以最大沉降量为因变量的参数敏感性分析

相关性系数和显著性系数计算结果如表5。

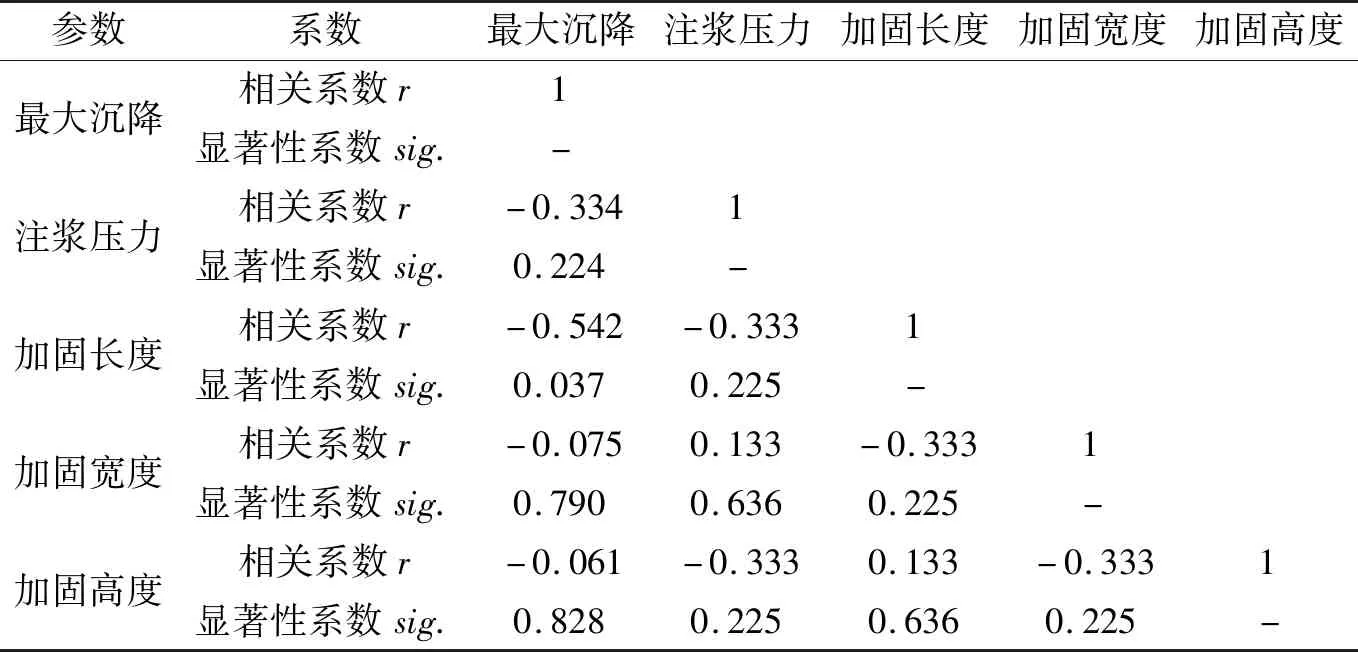
表5 各变量间的相关性系数和显著性系数Tab.5 Correlation coefficient and significance coefficient among variables

通过Pearson′s相关系数,可以得到坡体的最大沉降与注浆压力(r=-0.334)、MJS加固长度(r=-0.542)、MJS加固宽度(r=-0.075)和MJS加固高度(r=-0.061)成负相关,即最大沉降随着这3个变量的增大而减小,这结果与实际是相符的。显著性系数越小,相关性越显著。本模型中影响因素的显著水平排序为：加固长度(sig.=0.037)>注浆压力(sig.=0.224)>加固宽度(sig.=0.790)>加固高度(sig.=0.828)。通常认为sig.<0.05时,为显著影响因子,在本次试验模型中,仅加固长度达到了高显著水平。

3.2.2 以安全系数为因变量的参数敏感性分析

相关性系数和显著性系数计算结果如表6所示。

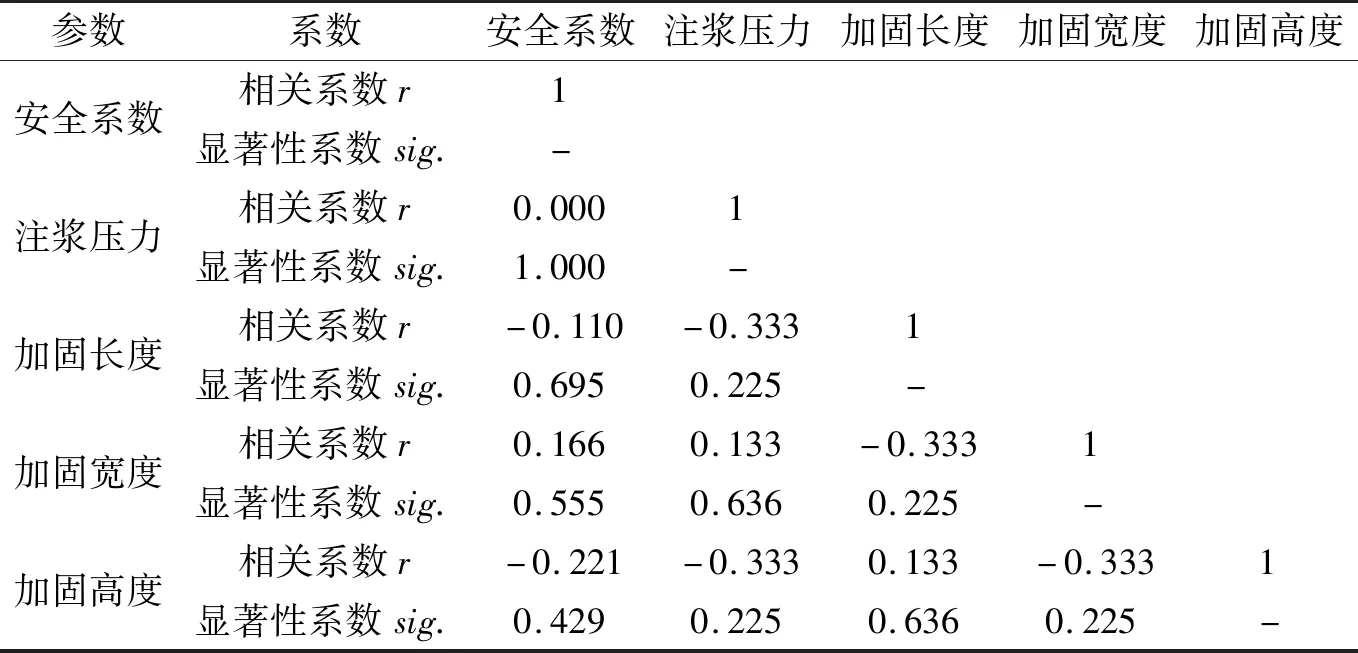
表6 各变量间的相关性系数和显著性系数Tab.6 Correlation coefficient and significance coefficient among variables

如表6所示,注浆压力(sig.=1.000)、加固长度(sig.=0.695)、加固宽度(sig.=0.555)和加固高度(sig.=0.429)的显著性系数均很大,在没有相关性显著因素的影响下,它们的显著水平仍十分低,表明这4个因素在试验范围内的变化对于安全系数的影响是微小的。

4 MJS加固参数优化

4.1 优化试验计算方案

由于均匀试验中仅加固长度L达到了高显著水平,因此仅对MJS加固长度L进行进一步的优化设计。同时增加支护压力Pt为变量,避免不同支护压力影响下L表现出不同的影响规律。追加试验计算方案如表7所示。

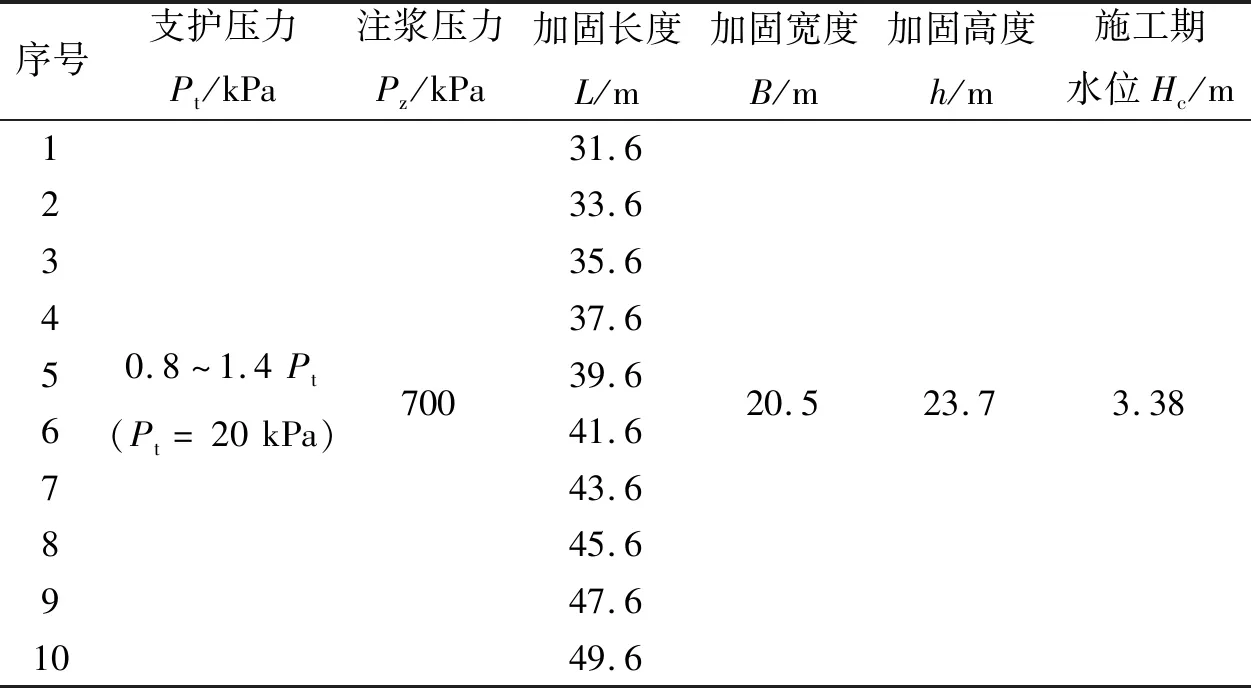
表7 优化试验计算方案Tab.7 Optimal test calculation scheme

4.2 加固长度影响分析

不同支护压力下最大沉降量随加固长度的变化如图6所示,沉降均为盾构机推进124 m时的数值。在试验范围内,随着L和Pt的增大,沉降越来越小,但是减小幅度不同。当Pt不变时,相比原始加固长度(L=35.6 m),L增大2～4 m的变化幅度较为明显,在合理支护压力选取的情况下,兼顾经济性原则,一般不宜选取太长的加固长度,因此建议选取37.6 m或39.6 m的长度,有利于进一步控制沉降大小。

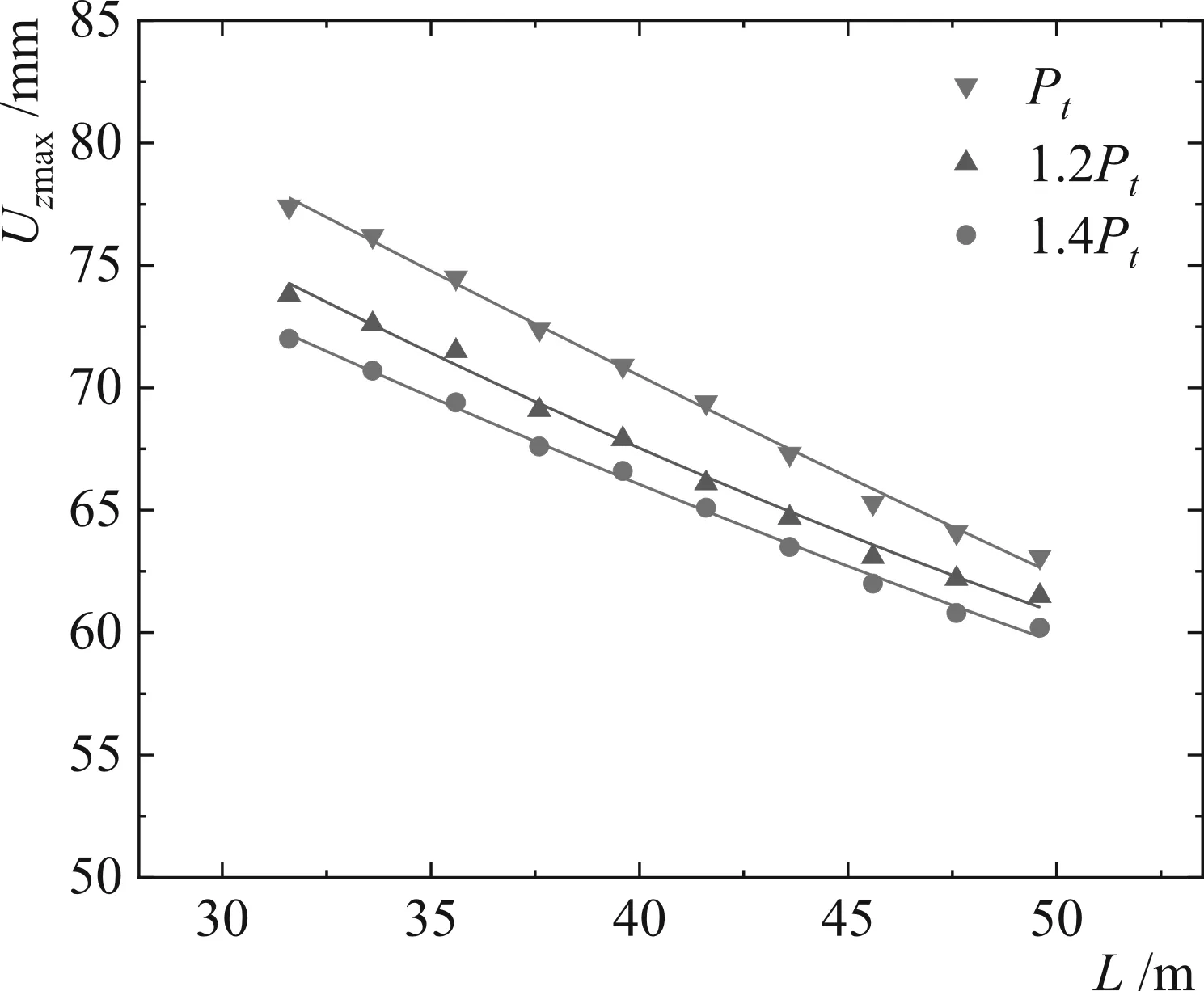
图6 不同支护压力下最大沉降量随加固长度的变化Fig.6 Variation of the maximum settlement with reinforcement length under different support pressures

4.3 支护压力影响分析

如图6所示,随着Pt的增大,拟合曲线的间距明显缩小,表明增大Pt时,最大沉降量减小的幅度越来越小,表明适当增大支护压力能够增强位移控制效果。图7为改变支护压力对沉降的影响云图,选取盾构推进100 m时的沉降为最终沉降,此时沉降已逐渐趋于稳定,变化不大。当支护压力为Pt和1.2Pt时,坡体和堤面的沉降为20～30 mm,而当1.4Pt时,坡体和表面沉降均有异常增大,为30～40 mm。

7-a 1.2 Pt,盾构推进124 m,Uz=79.55 mm 7-b 1.4 Pt,盾构推进124 m,Uz=74.51 mm

同时,支护压力对土体侧向位移影响显著。图8为改变支护压力对土体y向位移的影响。选取盾构推进84 m时的沉降云图,此时开挖面正好处于江堤中心,离MJS加固区域还有一段距离,能够清晰对比开挖面上的y向变形。当支护压力取0.8Pt(欠压)时,y向最大位移出现在开挖面上,此时支护压力明显不足,导致开挖面变形较大。随着支护压力增大,开挖面变形逐渐减小,y向最大位移转移到盾尾后的管片附近土体。当支护压力大于1.2Pt时,开挖面y向最大位移不超过20 mm。1.4Pt相比1.2Pt,最大y向位移明显减小,但是堤面和坡体内的部分位移增大。

8-a 0.8 Pt,盾构推进84 m,Uy=-60.03 mm 8-b Pt,盾构推进84 m,Uy=-51.85 mm

就变化数值来看,支护压力对y向最大位移的影响更显著,Pt相较0.8Pt,沉降的变化幅度为6.0%,而y向位移的变化幅度约为沉降的2倍。综合支护压力对侧向位移和沉降的影响,建议支护压力取值在1.2Pt上下浮动。数值模拟结果表明,增大支护压力能够控制最大沉降,同时支护压力对隧道附近土体变形的影响十分显著,支护压力不足容易引起开挖面变形过大,容易导致开挖面朝盾构前进方向的变形,从而引发上部土体的变形。因此,盾构穿越江堤的过程中为保证工程项目施工过程土体的安全和稳定,不能盲目增大支护压力来控制最大沉降,而要根据工程的实际情况在施工中选取适当的支护压力。