Presheath formation and area design limit satellite-based Langmuir probes

Chenyao JIN (靳琛垚),Chi-Shung YIP (叶孜崇),Haigang SUN (孙海岗),Di JIANG (江堤),Wei ZHANG (张炜),Guosheng XU (徐国盛)and Liang WANG (王亮)

1 Institute of Plasma Physics,Hefei Institutes of Physical Science,Chinese Academy of Sciences,Hefei 230031,People’s Republic of China

2 University of Science and Technology of China,Hefei 230026,People’s Republic of China

Abstract In this article,the effect of the finite conductive surface area of a satellite on the use of satellitebased Langmuir probes is reviewed in light of the basic theory of asymmetric double Langmuir probes (ADLPs).Recent theoretical and experimental studies have discussed electron sheath/presheath formation and the electron Bohm criterion along with their implications for satellitebased Langmuir probes.The effects predicted by the latest theory of the electron Bohm criterion were not experimentally observed and the experimental results remain supportive of a critical area ratio (AL/AS)crit=(mi/(2.3me))1/2 between the probe area AS and the satellite area AL as conventionally believed.A satellite-based Langmuir probe must satisfy this criterion to physically act as a single Langmuir probe.However,experimental investigations also found that high-energy electrons adversely affect (AL/AS)crit and a Langmuir probe’s signal quality by giving additional electron current to AL.Based on these results,a number of limitations of the maximum probe area are derived when designing satellite-based Langmuir probes,with consideration of both the aim of the satellite and the plasma where the satellite-based probe works.These proposed measures are expected to only partially alleviate the effect of the inadequate satellite surface area on the application of satellite-based Langmuir probes.Using a larger satellite to carry a Langmuir probe remains the most viable means to obtain precise space plasma parameters.

Keywords: space plasmas,satellite-based Langmuir probe,sheath/presheath,electric propulsion

1.Introduction

The Langmuir probe is one of the most common and fundamental plasma diagnostics.It is currently the only plasma diagnostic,with the exception of Thomson scattering,that can directly obtain the electron energy distribution function(EEDF).It has important advantages including simple structure,low construction cost,high disturbance resistance and relatively lightweight ancillary electronic systems.Therefore,it has a wide range of applications in fusion [1-3],plasma processing [4],space plasma [5-8] and electric propulsion testing [9].

One of the key aspects when designing a Langmuir probe system is the probe area,which determines the signal strength and accuracy.On satellites,Langmuir probes are designed to measure space plasmas with plasma density ranging from 102-107cm-3.Increasing the size of the probe tip is often the most direct way to ensure sufficient signal strength,as in the case of the semi-spherical Langmuir probe,with a diameter of 5 cm,used on the China Seismological Electromagnetic Satellite (CSES) [10,11].This probe size is orders of magnitude larger than that of probes used in almost all other lowtemperature plasmas (usually on the order of millimeters).

It is noteworthy that the effective geometry of the probe is determined by the sheath structure of the probe.Thus,the decision of whether to use a cylindrical,spherical or planar probe model for analyzing probe data is fundamentally based on the ratio of the probe physical radius to the Debye length.If the Debye length is much smaller than the probe physical radius,then the probe behaves as a planar probe.As the Debye length gradually increases to be comparable to or much larger than the probe’s physical radius,the probe gradually becomes an effective spherical probe,regardless of its physical geometry.Therefore,regardless of the probe’s geometric shape,if its physical radius is much larger than the Debye length,the probe is still described by the physical model of a planar probe.To obtain a clear saturation point in the I-V trace,one needs to minimize the effect of sheath expansion,making it desirable to design a planar probe,where the probe radius is much larger than the Debye length.However,this is often impractical due to the limited available area of a small satellite.

Previous studies found an area criterion of ion loss area to electron loss area,based on the theory of ion/electron sheath formation,which ensures that the probe does not perturb the bulk plasma [12,13].As a spacecraft,such as a satellite,is floating in space,the only the ion loss area is the conductive surface of the spacecraft,and the probe tip combined with the spacecraft surface can be regarded as an asymmetric double Langmuir probe (ADLP).A similar criterion has also been indicated above where this ADLP can act as a single Langmuir probe [14].This criterion limits the maximum probe area when designing a Langmuir probe for reliable measurements because the conductive surface area of the spacecraft is limited.In the past,the size of spacecraft,such as satellites and sounding rockets,was relatively large.Therefore,even Langmuir probes with centimeter-level diameters could meet the criterion where the probe area was less than 1/1000 of the spacecraft’s surface conductivity area,providing a sufficient design margin to obtain complete probe data[10].On the other hand,the recent promotion of low-cost micro/nanosatellites,such as CubeSats,has made the use of micro/nanosatellites for space plasma exploration increasingly popular[15-17].Due to the extremely limited space and electronic payload,the Langmuir probe may be the only feasible plasma diagnostic that can be carried on micro/nanosatellites in the foreseeable future.Compared to traditional spacecraft,the overall surface area of micro/nanosatellites is relatively small,which makes it extremely difficult to design Langmuir probes that have a larger area while still satisfying the criterion that the probe area should be less than 1/1000 of the spacecraft’s surface conductivity area.Therefore,understanding the physics of Langmuir probes on satellites and clarifying the limitation of the probe area are particularly important for the popularization and development of space plasma research.

According to conventional belief,the criterion of the ion loss area to electron loss area is derived from traditional Langmuir probe theory,which is based on our understanding of the sheath/presheath formation.When the probe is biased negatively with respect to the plasma potential,an ion sheath with an ion presheath is formed near the probe,while an electron sheath without an electron presheath is formed when it is biased positively.However,this physical picture has recently been challenged by emerging theoretical studies,leading to the necessity to revisit current Langmuir probe methodologies.In a series of recent experiments,the predicted effects proposed by these theories were not found on Langmuir probe diagnostics,but the effect of high-energy electrons on the current collection of Langmuir probes with larger area sizes has been observed.In this paper,we examine the impact of these theoretical and experimental studies on the design limitations of Langmuir probes for satellite applications.

2.Theory of presheath formation and characteristics of the Langmuir probe

2.1.Principle of the Langmuir probe

The Langmuir probe is basically a conductive surface immersed into the plasma,biased with respect to the plasma potential Vpto collect the electron or ion current from the bulk plasma.The bias voltage between the probe and the plasma causes the formation of a sheath structure near the probe and the probe selectively draws electrons with different energy when the bias voltage varies.This process ultimately provides information on the EEDF of the plasma [18].Figure 1(a)shows a schematic of a single planar Langmuir probe system.

However,in practical applications,the probe is generally biased with respect to the chamber wall (floating) or the satellite(floating)instead of being fully grounded.Therefore,the current between the probe and the chamber wall or the case of the satellite must be balanced.The actual Langmuir probe system is schematically shown in figure 1(b).As shown in the figure,in this arrangement,the probe with the surface collecting area ASand the chamber wall with collection area ALcomprise an effective ADLP.Note that here we consider the probe to be an ideal planar probe with a thin sheath,i.e.the sheath expansion effect can be neglected.This is to emphasize the effect of the finite area ratio between the probe and the satellite surface on the measurement of electron temperature.The electron temperature is determined from the exponential region of an I-V trace,which is not expected to be significantly affected by known geometric effects.A Langmuir probe of arbitrary physical geometry can be considered to be a planar probe if the Debye radius is much shorter than the probe’s dimension in all directions.For a probe with a thick sheath,the sheath expansion effect will increase the effective collection area of the probe,which in turn increases the electron saturation current of the probe.However,this is not expected to affect the exponential region that contains the EEDF information about the I-V traces,which is the key purpose of this section.This analysis is thus expected to be applicable to all Langmuir probes regardless of their physical geometries.

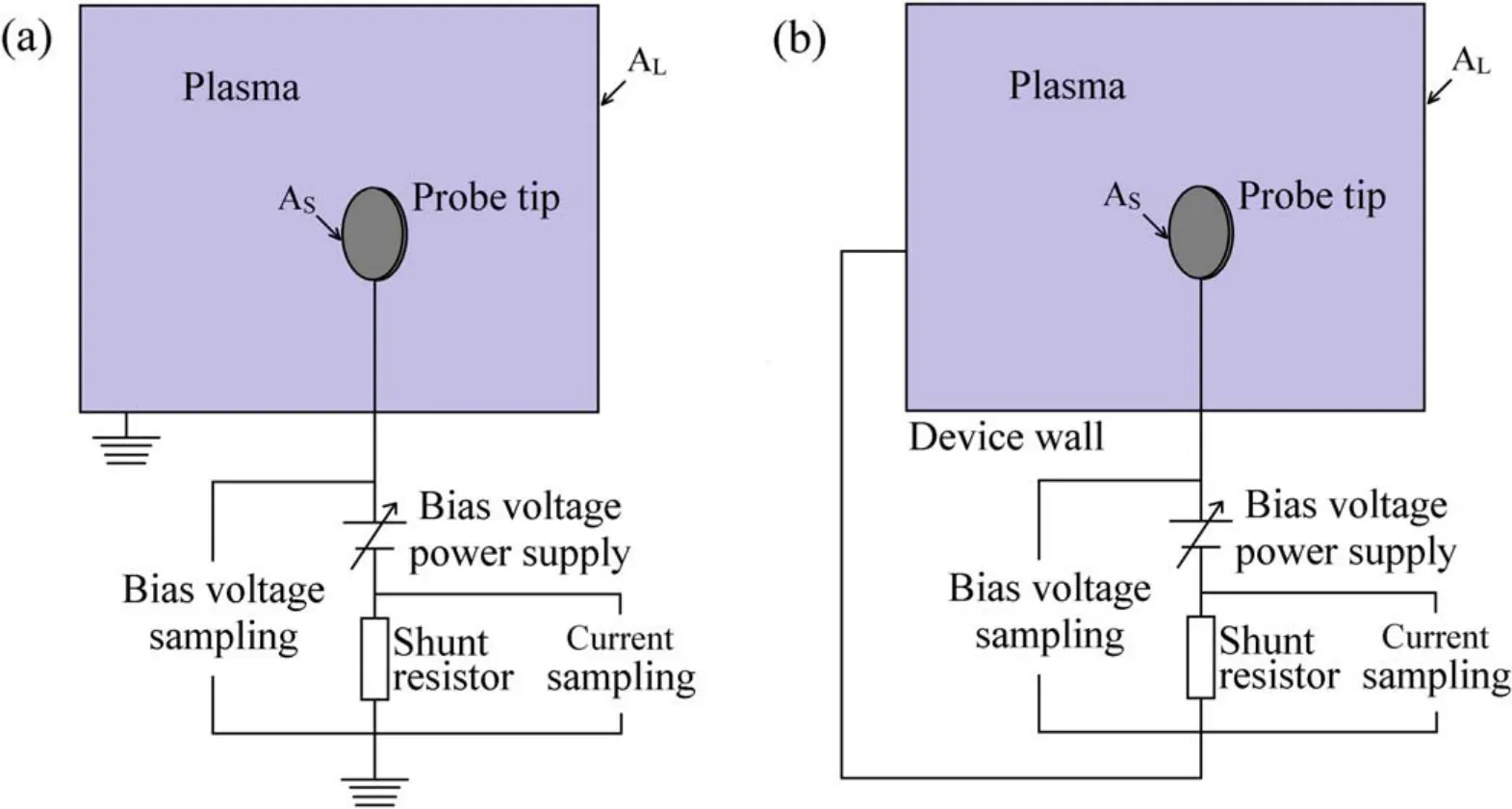
Figure1.Schematic of (a) the grounded single Langmuir probe system and (b) the floating single Langmuir probe system.

Then,the current balance between the ADLP system and the plasma can be written as,

where IL,e,IL,i,IS,eand IS,iare electron and ion currents of the large probe AL(chamber wall) and the small probe AS(the Langmuir probe),respectively.The current I to the ADLP can be given by,

The bias voltage of the large probe ALand small probe ASis defined as VL-Vf-Vpand VS-Vf—Vp,where VLand VSare the voltages of the large probe and the small probe,and Vfis the floating potential of the ADLP.Then,the current to the large probe ISand to the small probe IScan be derived:

where Teis the electron temperature in eV.Given that the ADLP is floating at Vf,the definition of the floating potential gives that the current to the probe is zero,and equations (3)and (4) can be written as follows:

Combined with equations(3)-(7),the following equation can be derived:

Then,I can be given by,

where φ=VS-VLis the bias voltage applied on one of the probe tips with respect to the other.When φ →∞and φ →-∞,I=-IL,isand I=IS,is,respectively,which agrees with the assumption that IL,is＜IS,es,i.e.the ion saturation current to the large probe is less than the electron saturation current to the small probe.Conversely,if IL,is＞IS,es,the ADLP will be saturated at IS,es.

Here,we consider two simple situations:

First,if AL=AS,i.e.IL,is=IS,is=Iis,equation(9)can be simplified as,

This is the formula for a typical symmetric double Langmuir probe [19].

Second,we consider another situation in which AL≫AS,i.e.the asymmetric double Langmuir probe situation,and here,IL,is≫IS,is,and dI/dVSand dI/dVLcan be derived from equations (5)-(7):

Given that ISis saturated at IS,es,it is known that if IL,is≫IS,es=IS,isexp(e(Vf+Vp)/Te),the right-hand side of equation (13) gives that dVL/dVSalways tends to zero in all cases.This is because when φ=VS-VL=0,the two probe tips are both floating at Vf,i.e.VS=VL=Vf,and the change in VLcan be ignored.In this case,the double Langmuir probe system can be directly simplified to a single Langmuir probe system with the small probe ASas the probe tip of the single Langmuir probe ALP,and neand Tecan also be derived.Since Ies=ALPene(kTe/2πme) and Iis=0.6ALPenecs,i,AL/AS≫((kTe/2πme)1/2/(0.6cs,i))=(mi/(2.3me))1/2will be satisfied for the situation when IL,is≫IS,es,where cs,iis the ion Bohm speed.This area ratio of AL/ASis also known as Гe,i,which is the ratio of electron flux to ion flux entering their respective electron/ion sheaths.Previous researchers believed that asymmetric double probes could act as a single Langmuir probe to accurately measure Teand neas long as the criterion of AL/AS＞ (mi/(2.3me))1/2was met [14].In addition,Baalrud et al experimentally studied the fundamental conditions for the formation of an electron sheath on a conductive surface immersed in a plasma and concluded that an electron sheath could only be formed for the conductive surface to be used as a single Langmuir single probe when the conductive surface area ASand the plasma device wall area AWsatisfy the criterion of AW/AS＞(mi/(2.3me))1/2[12,13].

The implementation of a double Langmuir probe is fundamentally based on the current balance between two probes.For an asymmetric double Langmuir probe,the effect that the ion current collected by the large probe ALoffsets the electron current collected by the small probe ASis extremely important in obtaining complete I-V traces as a single Langmuir probe.In other applications of a single Langmuir probe,ALrepresents the total conductive area of the vacuum chamber wall or satellite surface.Therefore,by utilizing the criterion of (AL/AS)crit＞(mi/(2.3me))1/2,which is derived from conventional theory,we can determine the maximum ratio of the Langmuir probe area to the conductive area of the chamber wall or satellite conductive surface.Table 1 lists the criterion of AL/AS＞(mi/(2.3me))1/2in various common scenarios.

Taking the cases of N+and O+as examples in table 1,the required area ratio of the probe to the satellite surface limited by the criterion is approximately 100 times,which may be multiplied by a factor of ten if one wants to satisfy the condition of ‘much greater than’.Since the plasma in the atmosphere at an altitude of several hundred kilometers ismainly composed of N+and O+,the generally adapted area ratio AL/AS＞1000 is derived from this calculation.Therefore,based on previous studies,it can be inferred that even with the extremely limited satellite surface area,the Langmuir probe on a satellite can measure neand Teaccurately as long as the probe is approximately 100 times smaller than the satellite.

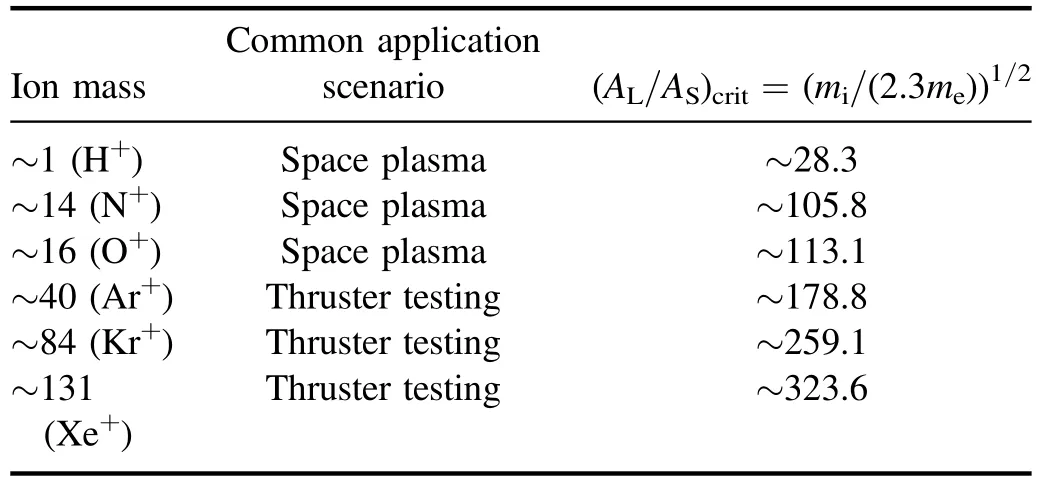
Table 1.Criterion of AL/AS ＞(mi/(2.3me))1/2 in some common scenarios.

On the other hand,if (AL/AS)critcannot be satisfied,in addition to affecting the electron saturation current collection of the Langmuir probe,it will also cause a significant change in VL,i.e.the potential of the satellite surface,as φ changes.If other devices on the satellite require a stable surface potential,then AL/ASmust be at least larger than (AL/AS)critby a generous margin.Purely from a physical perspective,VLis extremely sensitive to whether (AL/AS)critis satisfied.Figure 2 shows theoretically calculated results of the I-V traces and VS(solid line)and VL(dashed line)as a function of φ derived from equations (2)-(4) with different AL/ASof asymmetric double Langmuir probes in N+plasma.

As shown in figure 2,although the I-V traces change gradually and there is no obvious pattern transition,the evolution of VLwith φ can be obviously divided into two different regions: first,when AL/AS＜ (AL/AS)crit,VSincreases with increasing φ until IS=-IL,is,and then reaches a plateau,and then,at the same time,VLwill begin to decrease significantly.This is because ALcannot provide enough ion current to balance the increase of electron current to AS,which causes all further increases in φ to be allocated to VLto maintain the current balance.However,when AL/AS＞(AL/AS)crit,it is observed that the voltage of the two probe tips change in fundamentally different ways,where VSrises almost indefinitely,while VLremains nearly unchanged and only changes a little when VSis near Vp.This is because the electron current to AShas been saturated at IS,eswhen VSis near Vp,and IScannot further increase with increasing φ.Thus,the increase in φ is entirely allocated to VS.

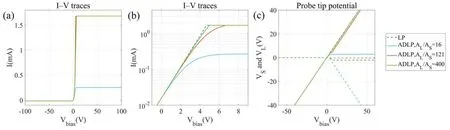
Figure2.Theoretically derived I-V traces plotted in(a)linear coordinate with ion saturation current and(b)semi-logarithm coordinate with ion saturation current subtracted and (c) VS (solid line) and VL (dashed line) as a function of φ of the ADLP with different AL/AS in N+plasma at plasma density ne=1010 cm-3 with a single-Maxwellian EEDF with Te=1 eV.Note that here we take the floating potential Vf as zero potential reference.

The calculation in figure 2 does not consider the sheath expansion effect[20].If this effect is considered,although the I-V traces can still be obviously saturated,as in the cases discussed above,VLwill still change slightly due to the additional increase in IS,esinduced by the sheath expansion effect.For an effective planar probe,this change will be relatively small.However,if a probe has a spherical effective geometry,sheath expansion is expected to cause ISto increase significantly even beyond electron saturation.This is expected to cause a much larger AL/ASratio to be needed.In all cases,as figure 2 shows,the stability of VLremains highly sensitive to AL/AS.Even a small variation in AL/ASnear(AL/AS)critis sufficient to completely change the way VLvaries with respect to φ.Therefore,if we have a clear understanding of the plasma ion species and there is no influence of high-energy electrons on IL(described below),the required AL/ASfor the Langmuir probe can be accurately estimated.

Recently,a series of theoretical studies proposed an electron presheath and electron Bohm criterion so that electrons do not enter an electron sheath with a random thermal flux,but instead with a fluid velocity known as the electron Bohm speed [21,22].Experimental studies aimed at testing the effects of this electron Bohm criterion instead revealed other mechanisms that affect the design limitation of the Langmuir probe area[23].These will be discussed in detail in the following sections.

2.2.Theory of presheath formation and particle loss balance

In section 2.1 of the previous discussion,we mentioned that AL/AS＞(mi/(2.3me))1/2is derived from the assumptions of Ies=ALPene(Te/2πme)and Iis=0.6ALPenecs,i,which assumes that ions enter the ion sheath with the ion Bohm criterion and electrons enter the electron sheath randomly at the electron thermal velocity.However,the escape velocity of ions and electrons entering their respective sheaths is determined by the sheath boundary conditions,also known as the sheath criterion.Therefore,it is necessary to understand the derivation processes of the sheath criterion.Here,we consider flux conservation,momentum conservation and the Poisson equation in the ion sheath/presheath region,assuming that the electrons satisfy the Boltzmann relation.The pressure gradient can be ignored because the ion temperature Tiis much lower than the electron temperature Te.Considering the sheath criterion(dρq/dx)≥0,i.e.the sheath starts at a spatial point where the plasma starts to deviate from being quasineutral,the conventional Bohm sheath criterion can be obtained [12,24]:

Since the pressure gradient is ignored,the ion velocity is only accelerated by the potential drop of the presheath,which requires that the presheath potential drop is～Te/2e to satisfy the Bohm criterion.The electron density in the presheath decreases as the potential drop decreases,according to the Boltzmann relation,and as a result,the electron density at the sheath edge is nee-1/2～0.6ne.

On the other hand,with a lack of direct diagnostics for the electron velocity distribution function (EVDF),the hypothesis that electrons enter the electron sheath randomly at electron thermal velocity was widely accepted without direct experimental evidence.Since 2015,Scheiner et al have explored the existence of the electron Bohm criterion and the presheath of the electron sheath corresponding to that of the ion sheath through a series of theoretical and numerical studies [21,25].Scheiner et al derived the electron Bohm criterion in a way that is almost symmetrical to the traditional ion Bohm criterion derivation.The formation of the electron sheath requires the application of a positive bias(with respect to the plasma potential Vp) to repel ions near the surface that are in contact with the plasma.Therefore,we can assume that the ions satisfy the Boltzmann relation.Differentiating the Boltzmann relation yields the following:

The momentum conservation in a collisionless electron presheath can be written as,

where veis the electron velocity.By inserting equation (15)into equation (16) and considering that the quasi-neutrality condition ne=niapplies,we obtain that the ratio of the electron pressure gradient to the electric field force is Te/Ti.Therefore,considering that Ti≪Tein low-temperature plasmas,the pressure gradient is much larger than the electricfield force.Furthermore,we consider the quasi-neutrality breakdown at the edge of the electron sheath,where net negative charge density begins to exist in space,that is(dρq/dx)≤0.Combining the flux and the momentum conservation in the electron sheath/presheath region without considering collisionality,we have the following:

Table 2.(AL/AS)crit in different scenarios in different plasmas.

Combined with equations (15)-(17) and the quasi-neutrality condition,the electron Bohm criterion,corresponding to the ion Bohm criterion,can be derived:

It is noted that this derivation of the electron Bohm criterion is similar to that of the ion Bohm criterion,which combines the flux conservation,energy conservation and Poisson’s equation to derive that the electrons enter the electron sheath with electron Bohm velocity.Consequently,Baalrud et al [12] proposed that the electron Bohm criterion can be satisfied by the electron flux associated with a truncated distribution,which gives ve,B≈ 0.9(Te/me)-1/2.Therefore,the presence of an electron presheath is not a necessary condition for electrons to flow to the probe with the electron Bohm criterion[26,27].In the absence of an electron presheath,the flux of electrons entering the electron sheath is～ALPeneve,B,and Гe,iis corrected to～1.67(mi/me)1/2.However,Scheiner and Baalrud also derived a potential spacious distribution for the electron presheath using an assumption of constant collision mean free path and constant collision frequency symmetrical to the ion presheath [12,25].

where λe-nis the electron-neutral collision mean free path.This series of studies has revealed several features of the electron presheath.First,the behavior of electrons in the presheath is essentially identical to how ions act in the ion presheath,which is a collisional process.Because the collision mean free path of electrons is significantly larger than that of ions,the length scale of electron presheath is much longer than that of ion presheath.Second,in contrast to the ion presheath,electron acceleration within the electron presheath is driven by the electron pressure gradient,according to equation (15),resulting in a much smaller potential rise in the electron presheath,which is only at the order of ion temperature.Third,according to Scheiner’s electron sheath/presheath theory,ions are assumed to obey the Boltzmann relation.Therefore,the ion density will drop by a factor of e-1/2due to the potential rise of the electron presheath.This corresponds to the drop by a factor of e-1/2of electron density at the ion sheath edge due to the potential drop of～Te/2e in the ion presheath.

If the electron presheath theory is accurate,the flux of electrons entering the electron sheath should be 0.6ALPeneve,B,which is similar in form to the flux of ions of 0.6ALPenecs,ientering the ion sheath.The flux ratio between electrons and ions entering their respective sheaths,Гe,i,must be corrected to (mi/me)1/2.

Based on the theoretical studies related to electron sheath/presheath theory mentioned above,we have summarized three theoretical predictions for Гe,i(Гe,i=(AL/AS)crit) in table 2 under three different scenarios.Electrons entering the electron sheath randomly at electron thermal velocity,electrons accelerated to the electron Bohm criterion in the electron presheath and electrons entering the electron sheath at the Bohm criterion without the presence of an electron presheath.Table 2 shows that the values of(AL/AS)critobtained under three different scenarios are significantly different by orders of magnitude.For micro/nanosatellites where the surface area is extremely limited,such large theoretical discrepancies are unacceptable.Therefore,it is essential to experimentally verify the correctness of the different theoretical (AL/AS)critvalues under current experimental conditions for the purpose of exploring plasma in space.

2.3.Experimental studies on the area limitation of the Langmuir probe

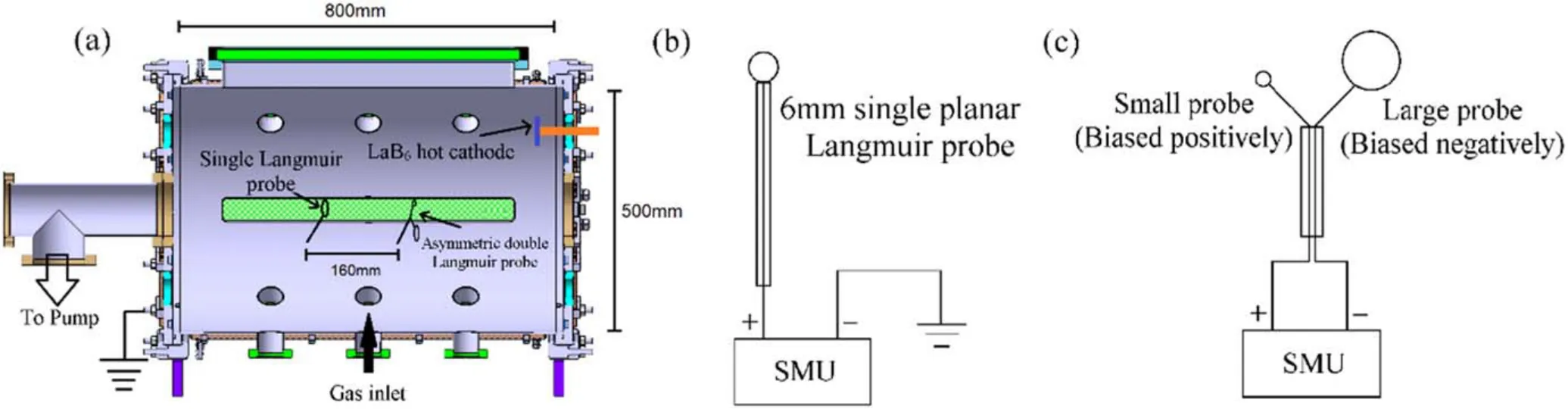
Figure3.Schematic of(a)DTS-II and the probe circuit of(b)the single Langmuir probe and(c)the ADLP.This diagnostics configuration is for experiments relevant to the asymmetric double Langmuir probe.

Previous experimental studies on Langmuir probes installed on satellites and sounding rockets have mainly focused on exploring situations where the current collected on the spacecraft surface is insufficient to balance the electron current of the probe due to a lack of conductive area or surface contamination.Shimoyama et al placed a 1:1 metal model of a sounding rocket in a large vacuum chamber with a diameter of 2.5 m and a length of 5 m filled with N2plasma.They tested the effect of reducing the surface area of the rocket on the Langmuir probe mounted on it by dividing the rocket model into three parts electrically and selectively connecting them to change the conductive surface area of the rocket.The results showed that even with AL/AS=124,the current collected by the conductive surface area of the rocket was still insufficient to allow the single Langmuir probe to obtain a complete I-V trace,leading to a 50% underestimation of the plasma density.However,the electron temperature measurement was not significantly affected [28].In this study,Shimoyama et al proposed that the problem of insufficient surface resistance of the spacecraft could be compensated via sweeping the bias voltage of the Langmuir probe fast(～3 kHz).Fang et al conducted simulations of micro/nanosatellites carrying a Langmuir probe in N2plasma in the laboratory and concluded that when AL/AS＜100,Langmuir probe could not reliably obtain plasma parameters and should be replaced by a resonance probe for parameter measurements[29].On the other hand,Tejumola et al used a double Langmuir probe to replace the single Langmuir probes on micro/nanosatellites [30,31].In addition,Bekkeng et al found that events such as meteorite falls could cause the spacecraft to be charged,and they suggested adding instruments to detect the surface potential of the spacecraft [32].Later,Leon et al measured the potential variation of the satellite shell caused by the Langmuir probe sweeping voltage via an additional high-impedance probe.They used this potential variation to correct the potential of the Langmuir probe to obtain a corrected I-V trace and claimed that this method can reduce up to～20%error of electron temperature measurement and up to～136% error of plasma density measurement [33].

In terms of experimental studies on the ratio of electron flux to ion flux flowing into their respective sheaths,Baalrud et al conducted a series of experiments in argon and helium plasmas and demonstrated that,in a uniform plasma,between a positively biased conductive electrode and the bulk plasma a double layer structure initially formed with a virtual cathode to reduce electron absorption,maintaining global current balance between the chamber wall and the electrode when AL/AS＜(mi/(2.3me))1/2[13].Baalrud’s group proposed the theory of electron presheath.Sun et al further suggested that plasma density measurements by the Langmuir probe should be corrected based on this theory[34].The electron presheath theory suggests that (AL/AS)crit=(mi/me)1/2.Yip et al discovered that even when the ratio of the area of the Langmuir probe area to the chamber wall area AL/ASis less than or near(mi/(2.3me))1/2as predicted by conventional theory,a small virtual cathode can still form near the probe,affecting the I-V curve and leading to a significant error of～30% in electron temperature measurement [35].Jin et al later conducted experiments in Diagnostics Test Source II (DTS-II) [23,36],as shown in figure 3(a),in argon plasma and scanned AL/ASof an ADLP ranging from 15-365 with the 2 mm diameter small probe ASunchanged and the diameter of large probe ALvarying from 8-40 mm.The plasma parameters were measured by a single Langmuir probe biased with respect to the grounded chamber wall and the ADLP is floating and its two probe tips were biased with respect to each other,as shown in figures 3(b) and (c).The bias is applied by a source measure unit (SMU).They analyzed each I-V trace and obtained variation of the saturation current with the changes of AL/AS.They concluded that (AL/AS)crit,Aris～180 for argon plasma,as shown in figure 4,which is consistent with the conventional theory prediction that ions enter the ion sheath with the ion Bohm criterion and electrons enter the electron sheath randomly at electron thermal velocity,given that (AL/AS)crit=(mi/(2.3me))1/2[23].

However,even when (AL/AS)crit=(mi/(2.3me))1/2,this study also found that there is a fundamental error in electron temperature measurement using an asymmetric double Langmuir probe in low-temperature plasmas.This is because in the laboratory and industry,plasmas are generally created by collisional ionization by high-energy electrons with the neutrals,and these high-energy electrons do not disappear after producing the plasma.They remain in the plasma to generate hot electrons.Therefore,the EEDF of the majority of laboratory and industry plasmas is not single Maxwellian but rather two-temperature or three-temperature Maxwellian.Studies of these two-temperature or three-temperature Maxwellian EEDFs in multi-dipole confined hot cathode discharge sources have a rich experimental history [37-40].Plasmas with multi-temperature Maxwellian EEDFs are common in industrial vacuum plasma sources as well[4,41].

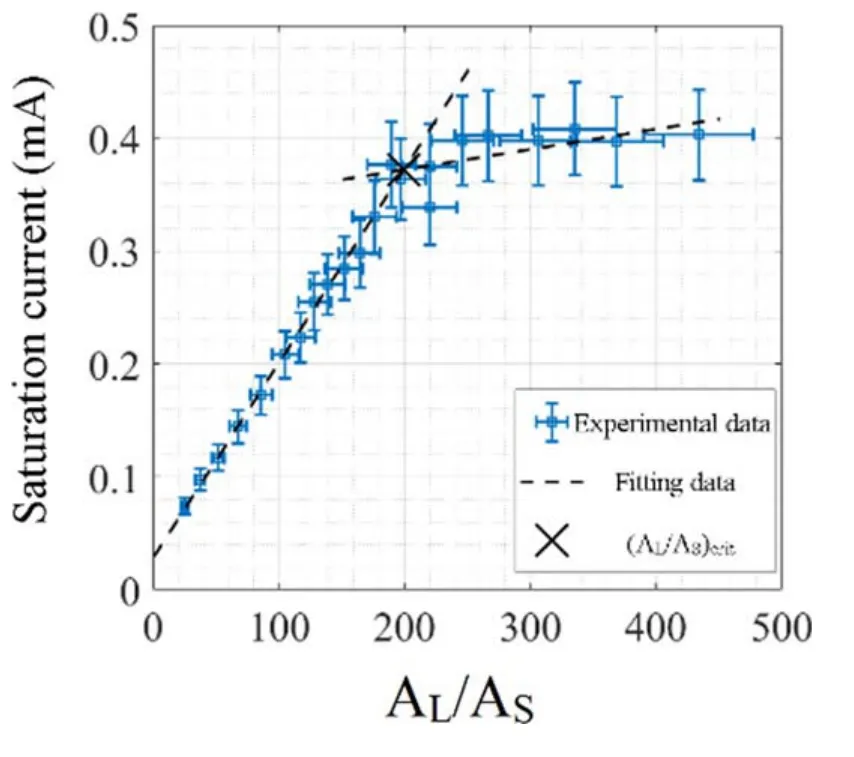
Figure4.Results of (AL/AS)crit obtained in DTS-II.

Reliable measurements using the ADLP fundamentally rely on the large probe ALto collect ion current offsetting the electron current collected by the small probe ASto maintain the current balance between the two probe tips.However,high-energy electrons are more difficult to exclude via the bias voltage applied to ALthan low-energy electrons,and this current contributed by the high-energy electrons neutralizes the ion current collected by AL.As a result,high-energy electrons systematically reduce the actual ion current provided by AL,distorting the I-V traces and causing false high electron temperature measurements.

This principle can be explained via correction of the formula of ADLP.Here,we correct the electron temperature in equations(3)and(4)with a multi-temperature Maxwellian EEDF:

where the subscript j represents the corresponding electron species in the multi-temperature Maxwellian EEDF.For example,in a two-temperature Maxwellian EEDF,the cold electrons are represented as‘cold’(ne,cold,Te,cold),and the hot electrons are represented as ‘hot’.In a three-temperature Maxwellian EEDF,there are additional primary electrons emitted from a hot cathode or heated by RF,which are represented as‘pe’for primary electrons or‘dp’for degraded primary electrons.Equations (20) and (21) describe the electron current in each species of electrons according to their respective temperatures following the Boltzmann relation and flowing into their respective probe tip,which contributes to the respective probe current,and then adds the ion current to form the I-V traces of the probe.

We cannot simplify equations (20) and (21) into a form similar to equation(14)to directly calculate the current of the probe,but we can still derive the I-V traces of the ADLP in different plasmas by numerically solving equations (20) and(21).Figure 5 shows the change in the I-V traces of the ADLP and the potential of the small probe VS(solid line)and the potential of the large probe VL(dashed line),where electrons follow a two-temperature Maxwellian EEDF.As shown in figure 2,in a plasma with a single-temperature Maxwellian EEDF,the I-V traces of the ADLP tend to converge with those of a single Langmuir probe as AL/ASincreases.However,as shown in figure 5,the introduction of 1% high-energy electrons ten times hotter than those in the bulk plasma is enough to cause two significant effects:

(1) The current contributed by high-energy electrons to the large probe ALeffectively reduces the net ion current collected by the large probe,resulting in the I-V trace not being clearly saturated at IS,eseven when AL/AS=(AL/AS)crit,i.e.AL/AS=104.04 in this case.

(2) High-energy electrons cause a distortion suppressing the I-V traces,especially near the region of the plasma potential,so that even if AL/AS＞(AL/AS)crit,the I-V traces still cannot reflect the real electron temperature.In the experiments in a multi-dipole confined hot cathode discharge source,we found that this effect can cause a false high electron temperature of approximately 30%,as shown in figure 6.It is noted that the magnitude of this false high electron temperature measurement is similar to that in previous experiments exploring the effect of virtual cathodes,and both studies were actually carried out in similar devices [35].This indicates that the formation of virtual cathodes and the distortion of highenergy electrons on the I-V traces of the ADLP are both manifestations of the change in the effective potential of the probe due to the global current balance between the probe and the chamber wall or the small probe and the large probe.

At the same time,these results also indicate that due to the presence of high-energy electrons,(AL/AS)crit,where the ADLP can act as a single Langmuir probe,will increase significantly.

The studies mentioned above were not carried out in devices or laboratories specifically designed for space plasma,but they are highly relevant to the application of Langmuir probe in space plasma.This is because the criterion of(AL/AS)critis a commonly used reference for low-temperature plasmas,and the basic physics underlying this criterion exists irrespective of the application scenarios.On the other hand,the aforementioned experimental works were mainly conducted in a multi-dipole confined hot cathode discharge source,where the plasma distribution is highly uniform,e.g.in the ADLP relevant experiments of Jin et al,the difference in plasma parameters between the two probes was less than 5%.Given that the ionosphere is a plasma with a vast scale and that the scale of the Langmuir probe on satellites and spacecraft probes is much smaller compared to the plasma itself,the ionosphere can be regarded as a uniform plasma rather than one with density gradient diffusion.Therefore,these experiments in a multi-dipole hot cathode discharge source can provide significant reference for determining(AL/AS)critin the ionosphere.

Figure5.Theoretically derived I-V traces plotted in(a)linear coordinate with ion saturation current and(b)semi-logarithm coordinate with ion saturation current subtracted,and(c)variation of VS(solid line)and VL(dashed line)with changes of φ of the ADLP with different AL/AS in a N+ plasma at plasma density ne=1010 cm-3 with a two-temperature Maxwellian EEDF consisting of 1% hot electrons with Te,hot=10 eV and 99% cold electrons with Te,cold=1 eV.Note that here we take the floating potential Vf as the zero potential reference.

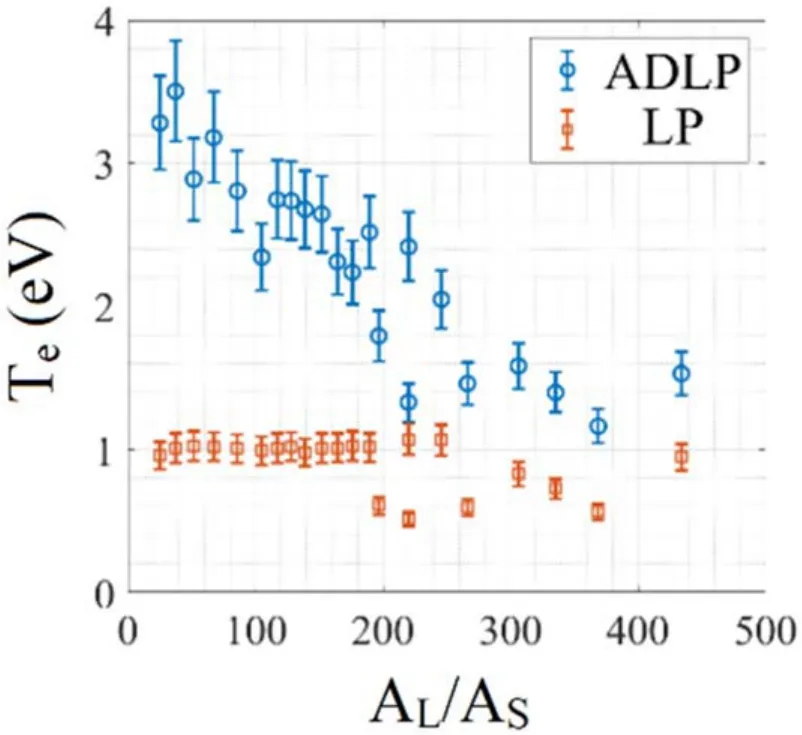
Figure6.Comparison of Te measured by the ADLP with different AL/AS and that obtained by the single Langmuir probe.

3.Design limitation of the Langmuir probe on satellites

3.1.Overview of the ion loss area of a satellite

When a satellite is launched,it floats in space without any electrical connection to the ground.Therefore,the Langmuir probe carried on the satellite and the satellite itself form a floating system in space plasma,which draws zero net current,as shown in figure 7.This means that the electron current absorbed by the Langmuir probe must be balanced by an ion current absorbed by the satellite’s metal shell,and vice versa.Consequently,the Langmuir probe carried on the satellite can be regarded as an asymmetric double Langmuir probe system,and the formation of its I-V traces was dictated by the physical principles relevant to the ADLP.

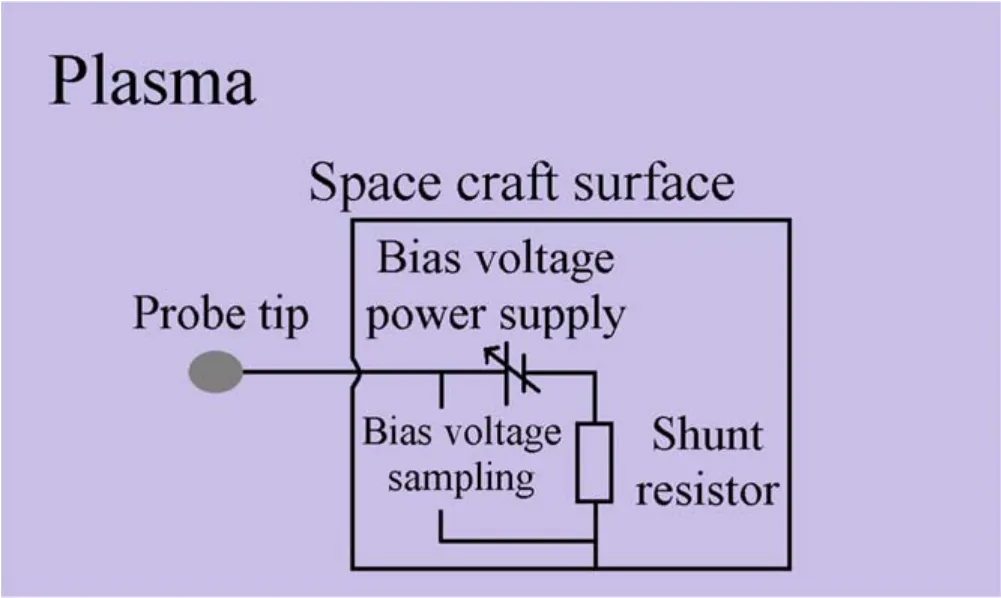
Figure7.Schematic of the circuit composed of the Langmuir probe and the satellite.

The outer surface area of the satellite’s shell that collects current can be defined as the ion loss area AL,as described in section 2,while the Langmuir probe can be regarded as the electron loss area AS.Here,the outer surface area of the shell that collects current is not the physical surface area of the shell itself but the conductive area where the satellite can actually collect current and balance the current collected by the Langmuir probe.Therefore,devices such as solar panels directly mounted on the satellite’s surface,which require insulation between them and the shell,cannot be considered as part of ALsince they cannot collect current.As a result,due to the presence of these insulated surface devices,ALis generally smaller than,or even significantly smaller than,the total surface area of the satellite.

3.2.Example of evaluation of the probe area of the Langmuir probe on satellites

Considering that the most popular micro-or nanosatellites in the future are likely to be designed as standard CubeSat,we can use the specification of CubeSat as a calculation example for the probe’s maximum area.The volume specification of a CubeSat is in units of U (a 10 cm × 10 cm × 10 cm cube),and each CubeSat can be treated as a 3D stack made up of 1U cubes.When the satellite’s volume is only 1U,its total surface area is about 600 cm2.According to the formula AL/AS=(mi/(2.3me))1/2,the allowable probe area in a N+plasma is approximately 5.67 cm2,which is approximately a planar probe with a diameter of 1.9 cm or a spherical probe with adiameter of 1.34 cm.It is noteworthy that in a plasma with an electron density range of 102-107cm-3and an electron temperature of approximately 1 eV,the Debye length ranges from 2.3-230 mm.Considering that only in the planar Langmuir probe is the probe radius much greater than the Debye length,which provides more reliable diagnostic results,the diameter of the probe is only suitable for measuring plasmas of regions with higher density in the radiation belt.In addition,according to Ies=ALPene(kTe/2πme)1/2,the electron saturation current that this probe can obtain is between 1.5 nA and 0.15 mA.In particular,in low-plasma density environments,the signal intensity requires extremely strict performance of the probe electronic system.Furthermore,considering the solar panels installed on the satellite and flight-induced wake field effects (will be discussed in detail in section 3.3),micro/nanosatellites generally do not have the entire surface available for the collection of ion flow.This further compresses the maximum area of the probe,thereby further reducing the availability of a Langmuir probe on satellites.On the other hand,as the volume of satellites increases,the available probe area will also increase.Table 3 lists the available Langmuir probe area and diameter for CubeSats from 1U-4U,assuming that there are no insulated surfaces such as a solar panel.As shown in the table,since the CubeSat connection surface is not exposed,the increase in volume does not linearly increase the probe area.In addition,the 4U cube array has more connection surfaces,and so the increase in probe area is also smaller.It is noteworthy that the surface area here is calculated as physical area.In a practical setting,the effective area of both the probe and the satellite will expand due to the sheath expansion.However,since the effective part of the probe data is the part where the probe is biased close to the plasma potential,the impact of sheath expansion on the probe area will be much smaller than the expansion of the satellite surface area,and so there will be a small margin for the probe area due to the more obvious sheath expansion of the satellite surface.As the satellite enters an area with lower plasma density or higher electron temperature,the corresponding Debye length of the local plasma will increase,and thus this margin will also increase moderately.

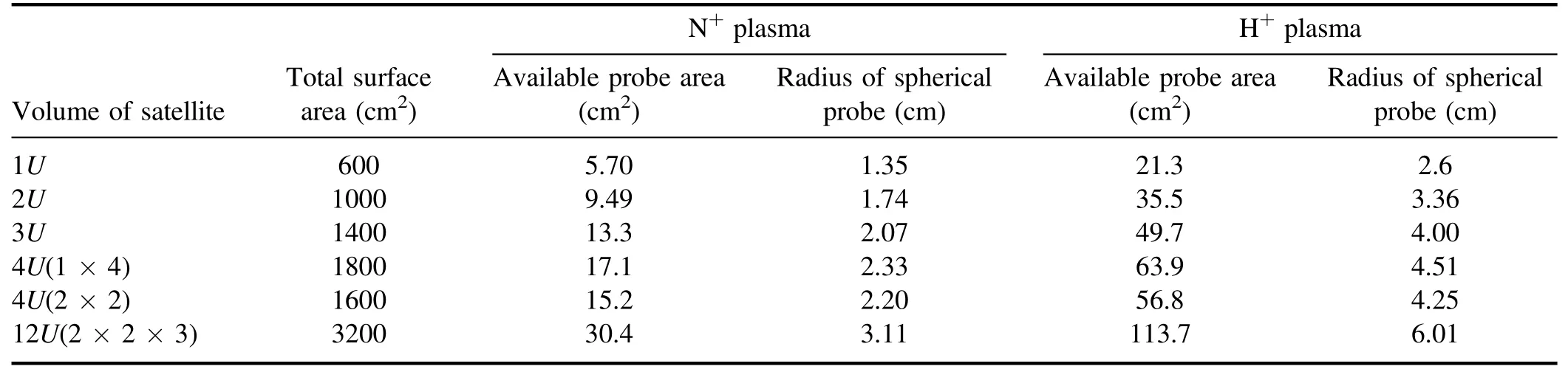
Table 3.The limitations of diameter and area of the Langmuir probe on satellites with different surface areas in N+ and H+ plasmas,respectively.

It can also be seen that as the ion mass decreases,the available probe area increases.This reflects the characteristic of AL/AS=(mi/(2.3me))1/2decreasing as midecreases.There is a difference in the composition of space plasmas at different altitudes,and since the baseline condition for the probe is AL/AS=(mi/(2.3me))1/2,the lighter the ions in the plasma(i.e.closer to proton mass),the larger the available probe area.Considering gravitational effects,the mass of ions in the plasmas is expected to be lighter at higher altitudes,and thus,as the planned orbit altitude of a satellite increases,its Langmuir probe can also be appropriately enlarged.In addition,when a satellite moves relative to the plasma,it generates a wake field affecting the effective current collection of the satellite surface and further decreases the available probe area,which depends on the composition and flow velocity of the background plasma.

Figure 8 illustrates the variation in the ten-fold Debye length with the change in plasma density at electron temperature Te=1 eV.As shown in figure 8,even for a micro-and nanosatellite with a volume of 12U[42],the Langmuir probe it carries can only satisfy the planar probe condition,i.e.a probe radius much greater than the Debye length,in relatively high-density space plasmas (106-107cm-3).Therefore,we can conclude that probes carried by satellites smaller than this size will act as a spherical probe shape in almost all space plasmas,and spherical Langmuir probes will result in greater sheath expansion [19,43,44].A highly spherical sheath geometry necessitates the use of the inflection point technique to determine the saturation current due to the lack of clear saturation,or a sharp ‘knee’ of an I-V trace.However,the inflection point technique is itself prone to the current balance effect described in section 2 [35].Some CubeSat missions employ non-spherical probes with significantly smaller area than this critical value due to the lack of conductive surface on the satellite [16],which might further complicate this issue.In addition,since sheath expansion will cause the Langmuir probe to collect more current when the probe is biased above the plasma potential,it will have a greater impact on the surface potential of the satellite,as discussed previously.

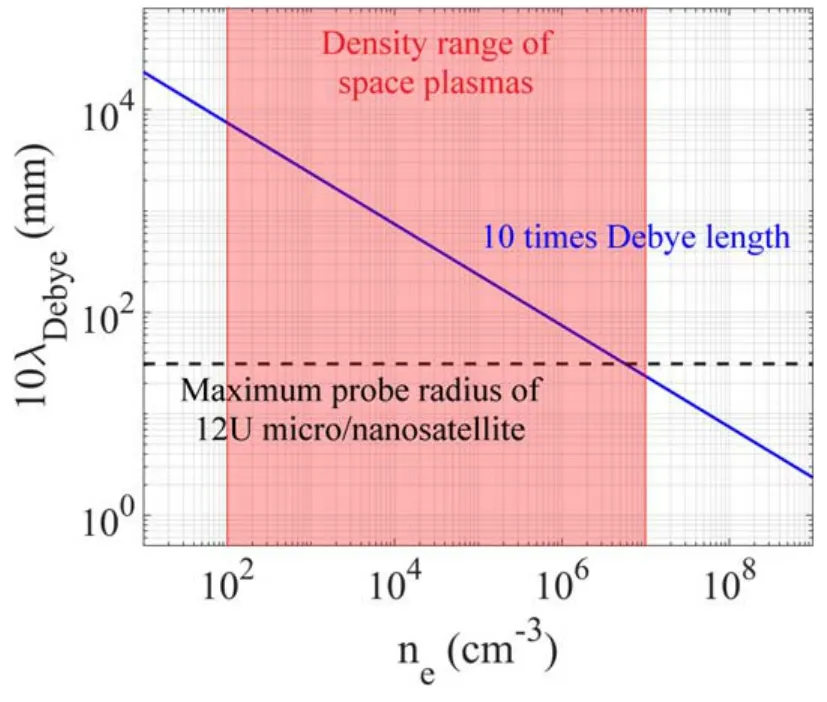
Figure8.Variation of ten times Debye length with the change in the plasma density compared to the maximum probe radius of a 12U micro-and nanosatellite.

In addition,as demonstrated by the experimental and numerical results in section 2.3,the presence of high-energy electrons can significantly increase the required AL/ASratio for the Langmuir probe on satellites to obtain a reliable electron temperature.However,if researchers can tolerate an electron temperature measurement error of 30%-50%,satisfying AL/AS=(mi/(2.3me))1/2will still provide results that are correct at least on the order of magnitude.This is more accurate than using a double Langmuir probe to replace a single Langmuir probe.However,in this case,the stability of the satellite surface potential cannot be guaranteed.This underscores another point.In a plasma where there are no high-energy electrons or where the electrons have a singletemperature Maxwellian EEDF,such as a plasma generated mostly by photoionization,any double Langmuir probe with any ratio of AL/AScan obtain accurate plasma temperature and accurate plasma density,as long as the areas of the two probe tips or the probe area and the satellite surface area are known.However,for most space plasmas,high-energy electrons themselves are important for the plasma production processes [45,46],and it is unrealistic to ignore the effect of high-energy electrons.This also raises questions about the reliability of using a symmetrical double Langmuir probe to measure electron temperature in this plasma with complicated EEDF instead of single-Maxwellian EEDF,as its theory assumed.

It is worth noting that almost any deployable structure on a satellite can be used to supplement the ion loss surface area ALof the satellite,especially if it can be made into a conductive surface for cooling.It is useful if the solar panels are deployed away from the satellite body,or the side made by conductive material without solar panels being shielded by facing the direction of flight,to increase the conductive surface area of the satellite,releasing the loss surface that was originally blocked by the solar panels.As a result,the available area of the Langmuir probe on the satellites could increase.

3.3.Effect of wake field on limitation of the Langmuir probe area

When a probe is immersed in a sheath where ions enter the sheath accelerated in the presheath,a wake field exists due to the ion motion relative to the probe,causing a significant reduction in ion current to the probe surface facing the wake field region.This is also the fundamental reason that the Langmuir probe cannot effectively measure the plasma potential in the sheath/presheath region[47,48].Similarly,to maintain altitude,a satellite needs to reach the first cosmic velocity,which is approximately 7900 m s-1,approximately 80%of the Bohm velocity of hydrogen plasma at an electron temperature of 1 eV,and three times the Bohm velocity of nitrogen plasma at an electron temperature of 1 eV.This situation results in two consequences.First,the Langmuir probe itself generates a wake field,causing a corresponding decrease in the current collected by the rear of the probe relative to the flight direction.At the same time,the ion current IL,iscollected by the backside of the satellite facing the flight direction also significantly decreases,reducing the amplitude of the Langmuir probe electron current balanced by the ion current collected by the ion loss surface.This effect may lead to an increase in (AL/AS)crit.Under a conservative estimation,we can consider the surface of the backside of the satellite relative to the flight direction as not contributing to the ion loss surface and calculate the corresponding available area of the Langmuir probe.On the other hand,planning the flight direction of the satellite to orient the surfaces that cannot collect current,such as solar panels,towards the backside of the flight direction of the satellites,will effectively increase the available area of the Langmuir probe.

4.Conclusion

In this work,we investigated the effect of the sheath/presheath formation and electron Bohm criterion theory on the application of Langmuir probes.In our experimental results,we did not find the predicted effects of the electron Bohm criterion theory on the electron saturation current of the Langmuir probe as proposed by Baalrud et al and Sun et al.Although this experiment does not directly refute Baalrud’s electron sheath and presheath and electron Bohm criterion theory,it does demonstrate that the traditional theory,which predicts that the ratio of probe area ASto device wall area ALmust be lower than (AL/AS)crit=(mi/(2.3me))1/2,is still valid.In addition,the numerical simulation and experimental results indicate that the potential fluctuation of the satellite surface when the probe area is too large,and the effect of the virtual cathode formed near the probes in plasma devices affecting the accuracy of electron temperature measurements,are both fundamental plasma physics processes caused by the global particle loss balance of the plasma.High-energy electrons also have a detrimental effect on(AL/AS)critand the accuracy of the electron temperature measured by the probe.Therefore,this effect should also be considered when designing a Langmuir probe.

Furthermore,we have extended the relevant experimental results to the area limitation of the Langmuir probe on satellites and proposed a series of minimum technical requirements for designing and deploying Langmuir probes on micro/nanosatellites.Since multiple elements,such as the EEDF and ion species of the plasma,altitude and flight direction of the satellite,will significantly affect the measurement accuracy of the Langmuir probe,it is necessary to understand the composition and generation processes of the plasma to be measured by the satellite to make precise adjustments to the overall design of the satellite and its mission process to adapt the use of Langmuir probes,alleviating the factors that affect the probe performance.

In addition,the signal of the Langmuir probe on micro/nanosatellites is expected to be very weak and requires a high-precision and high-sensitivity electronic system to achieve a high signal-to-noise ratio.Increasing the surface area of the satellite and directing its conductive surface towards the plasma as much as possible can effectively increase the available probe area and design threshold.In addition,due to the effects of sheath expansion and highenergy electrons on the ion loss area of the satellites,data analysis for the Langmuir probe on micro/nanosatellite would be significantly complicated.On the other hand,adding direct measurements on the potential fluctuation of the satellite can effectively correct probe potential and obtain accurate I-V traces[33].Note that potential fluctuation effect would also largely disturb the time-averaged probe measurements because the I-V traces shift following the oscillated floating potential of the satellite,and the averaged I-V traces would be flattened and give a false high electron temperature.This is an effect similar to RF fluctuation effects in RF plasmas,which has been well studied in laboratory settings [49,50].This effect is fundamentally different to the effect of inadequate loss area discussed in this work.If the probe itself does not meet the criterion(AL/AS)crit,the I-V traces cannot saturate,and the plasma density cannot be correctly obtained.In addition,the bias on the probe would significantly affect the potential of the satellite in this case.This potential fluctuation,in turn,would further decrease the accuracy and reliability of the Langmuir probe on the satellite.In summary,the application of Langmuir probes on micro/nanosatellites is a task with high technical risk since the available engineering margin is severely limited by the underlying physical processes of Langmuir probe operation.If high-precision plasma physical parameter measurements are needed,it will be more reasonable to employ Langmuir probes on larger conventional satellites.

The issues presented in this paper also have some impact on the application of the Langmuir probe in thruster testing,although the specific situation is slightly more complicated than that of the Langmuir probe on satellites.On one hand,the generally large diffusion chamber used in thruster testing ensures that the electron loss area of the probe ASis very small compared to the overall ion loss area of the chamber wall AL.On the other hand,the plasma that is able to diffuse to the diffusion chamber wall that forms a sheath and presheath is much lower in density compared to that in the plume and internal plasma of the thruster.Moreover,the possible presence of ion-neutral collisional friction in different scenarios results in a relatively low ion flux actually arriving at the diffusion chamber wall.These issues also create limitations on the design of the probe area of the Langmuir probe,which would also be an interesting work in the future.

Acknowledgments

The authors gratefully acknowledge the late Dr Noah Hershkowitz,Irving Langmuir Professor Emeritus of the University of Wisconsin-Madison and our long-time collaborator,who has given invaluable advice and suggestions to the studies associated with sheath/presheath and diagnostics associated physics.This work is supported by National Natural Science Foundation of China (Nos.12275305 and 12205334),the Chinese Academy of Science Hundred Youth Talent Program,China Postdoctoral Science Foundation(No.2022M713188)and the Director’s Fund of Hefei Institutes of Physical Science,Chinese Academy of Sciences (No.YZJJ2022QN19).

ORCID iDs