雨、潮联合作用下防洪设计的不确定性分析

裴昊川,倪 倩,甘富万,3

(1.广西大学 土木建筑工程学院,南宁 530004;2.广西珠江委员会南宁勘测设计院,南宁 530007;3.广西防灾减灾与工程安全重点实验室,南宁 530004)

近些年来,Copula函数在解决洪水、降雨、干旱等多变量水文联合分布问题上应用广泛。潘国勇等[1]采用Copula函数构建了武澄锡虞区的雨、潮联合风险模型,并分析该地区雨、潮组合风险率,为武澄锡虞区的防洪治涝提供了新的科学依据;许翰卿等[2]应用二元Copula函数构建沿海地区极端降水和风暴增水两变量联合风险模型,为防汛工程抵御复合洪涝灾害的设计标准提供了新的设计方法;蔺文慧等[3]采用混合Copula函数构建马达瓦斯克流域洪水历时、洪量及洪峰流量混合模型,对比单一Copula函数拟合效果更优,能更加全面表征变量间相关关系。本文以北海市铁山港区入海明渠为研究对象,采用北海站雨量资料和石头埠潮位站潮位资料进行两变量分析,首先分析雨、潮联合概率分布特征,其次引用了一种考虑雨、潮与调洪耦合的防洪重现期,并将其与常见的OR、AND重现期进行对比分析,最后基于蒙特卡罗法分析抽样不确定性对于雨、潮共同作用下明渠设计水深的影响,此研究为雨、潮作用下的入海明渠的设计水深确定提供了一条新的设计思路。

1 研究方法

1.1 Copula函数

Copula函数可以将多个具有不同形式边缘分布的随机变量联结起来构造联合分布。令雨量X的概率分布为FX(x),潮位Y的概率分布为FY(y)。依据Sklar定理,X和Y的联合分布函数可以用Copula函数C表示成f(x,y)=C(u,v)[4],其中u=FX(x),v=FY(y)。

f(x,y)相应的联合概率密度函数可表示为

f(x,y)=C(u,v)fX(x)fY(y)

(1)

式中：C(u,v)=∂C(u,c)/∂u∂v为Copula函数的密度函数;fX、fY分别为X和Y的概率密度函数。

在现阶段水文气象领域中,通常采用Archimedean Copula函数族函数构建多变量水文联合分布模型[5-6]。4种常用的Archimedean Copula函数见表1。

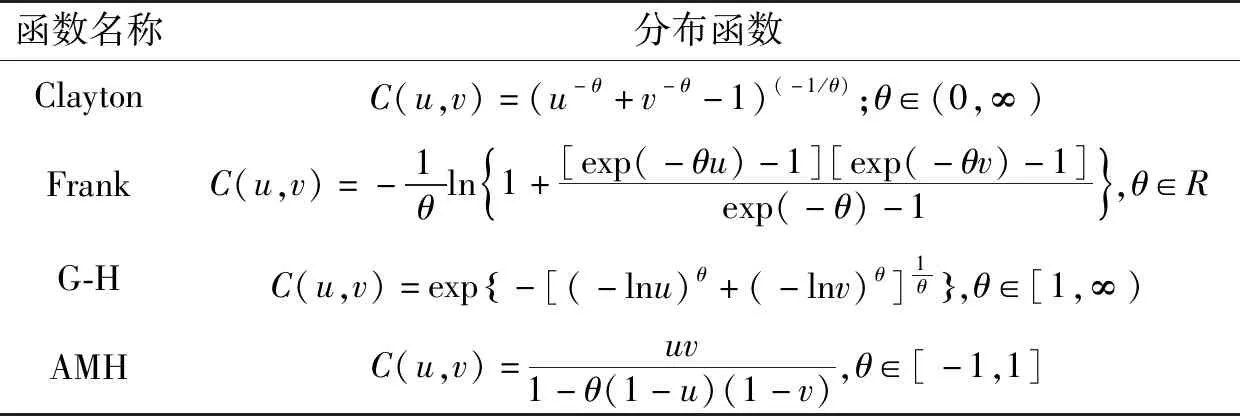
表1 4种常用的Archimedean Copula函数Tab.1 Four commonly used Archimedean Copula functions

1.2 OR、AND重现期和防洪重现期

AND重现期指所研究区域降雨量和潮位同时超过某一特定阈值。

OR重现期指所研究区域降雨量或潮位其中一个超过某一特定阈值。

定义如下

TOR=1/P(X>x∪Y>y)=1/[1-C(u,v)]

(2)

TAND=1/P(X>x∩Y>y)=1/{1-u-v+C(u,v)}

(3)

根据OR和AND重现期定义,在同一重现期水平下,有无数种设计雨、潮组合;这表明设计雨、潮重现期和设计雨、潮组合之间并没有一一对应的关系,这将给水利工程的运行带来了巨大风险。因此,针对类似雨、潮组合等二变量水文事件的设计重现期问题,甘富万等[7]在研究干、支流洪水二变量共同作用下的防洪设计时,提出了防洪重现期的概念,即由洪水(雨、潮)等作用所确定的防洪参数F超过工程防洪(防潮)设计的给定值f的平均间隔时间,在本文中可以表示为

Tf=1/[F>f设=f(x,y)]

(4)

式中：F为雨、潮设计的防洪参数;x和y分别为雨量和潮位。

黄强等[8]认为最可能组合模式可以有效节省工程费用,在同时满足工程防洪标准的条件下,其模式代表雨量、潮位联合设计值取最大值的情况,其表达式如下

(um,vm)=argmaxf(u,v)

(5)

f(u,v)=C(u,v)f(x)f(y)

(6)

式中：C(u,v)为雨量、潮位联合分布的概率密度函数;f(x)和f(y)为边缘分布的概率密度函数。

1.3 不确定性度量指标

本文利用尹家波等[9]提出的平均横向偏移程度DX、平均纵向偏移程度DY、置信区域面积S和平均欧氏距离d作为两变量估计不确定性的度量指标。DX、DY分别用于度量雨量、潮位与实测样本系列推求的设计值在一维空间的估计偏差;S和d用于度量模拟设计值点据与实测样本系列设计值的空间距离。计算式如下

(7)

(8)

(9)

1.4 基于防洪重现期的设计水深计算

(1)分别建立雨、潮组合的边缘分布函数u=F(x)和v=F(y),并依此构建并选取雨、潮组合的最优Copula函数模型C(u,v);

(2)产生样本容量为n的范围在(0,1)的随机数n1和n2,设n1=u,由条件概率公式求解出每一个与u相关的v,即令C(v|u)=∂C(u,v)/∂v=n2;

(3)根据雨、潮最优边缘分布函数,反推每个随机组合(u,v)所对应的雨、潮组合的设计值(x,y),带入调洪模型计算出每个设计断面的设计水深;

(4)对每个断面的n个水深值进行排序,根据水文计算方法计算出不同设计重现期水平年的设计水深h设。

1.5 基于Monte Carlo Method的抽样不确定性分析

(1)与上述(1)和(2)步骤相同,获得样本容量为n的二元雨、潮组合样本;

(2)重复上述步骤N次,便可得到N组与样本容量n相同的二元雨、潮组合样本。对N组二元雨、潮组合样本使用实测样本序列的估参方法即可得到N组参数值;

(3)在每一组参数下,给定OR重现期TOR,利用式(5)和式(6)得到特定重现期下N组参数对应的N组最可能组合联合设计值。对于N组最可能联合设计值,采用核密度估计方法得到给定某一显著性水平α的(1-α)置信区域,置信区域越大,表明联合设计值不确定性越大;

(4)在每一组参数下,给定防洪标准T,计算OR重现期标准下的设计水深。在OR重现期标准下,将步骤(3)中得到的N组最可能设计组合值代入调洪演算模型可得到N个水深设计值zOR。从而可求得重现期标准的单变量z点估计和置信区间。置信区间宽度越小,设计水深不确定性越小。

2 案例研究

铁山港区是广西地区面向东南亚的重要出海港口,该区在夏季易受台风的侵袭,台风带来强降雨以及洪暴潮,且该区域降雨主要集中5月至9月,故通过规划入海明渠实现区域内洪涝积水自流入海,以应对洪潮灾害。北海铁山港工业区排水明渠起点在北海至铁山港一级公路和规划的铁山港铁路支线的交叉口附近,终点至铁山港港口,全程自流排放,最后注入大海。线路全长约7 996.602 m,干渠设计雨水排泄流量为166.09 m3/s。本文以北海市铁山港区入海明渠为研究对象,降雨量资料采用北海站实测连续42 a年最大降雨量序列,潮位资料采用降雨量对应石头埠潮位站实测年最大潮位序列。

2.1 边缘分布及联合分布的确定

降雨量X代表北海站实测连续42 a年最大降雨量序列,潮位Y代表降雨量对应石头埠潮位站实测年最大潮位序列。采用AIC和RMSE准则[10]对皮尔逊III型(PE3)、Weibull分布、广义Logistic分布(GLO)和广义极值分布(GEV)4种雨量、潮位边缘分布函数进行评估,AIC和RMSE准则评估数值越小,则雨、潮边缘分布模型效果越优,由表2可知皮尔逊III型(PE3)函数构建雨量和潮位序列边缘分布模型效果最优。

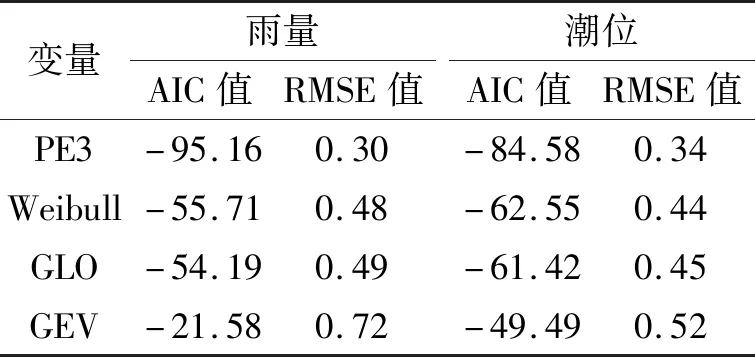
表2 雨、潮边缘分布计算结果Tab.2 Calculated results of rainfall and tidal level margin distribution

根据皮尔逊III型(PE3)函数所构建雨量和潮位序列边缘分布模型可以得到不同设计频率下的雨量和潮位计算结果,表3为设计频率为 1%、2%、5%、10%及20%所对应的雨量和潮位设计值。

表3 雨量、潮位资料PE3分布拟合计算结果Tab.3 Rainfall and tide level data PE3 distribution fitting calculation

采用Archimedean Copula函数族中的G-H、Clayton、Frank和AMH函数构建降雨量X和潮位Y联合分布模型,Copula函数参数θ由Kendall秩相关性系数法求得,采用BIC准则、RMSE准则和AIC准则可以有效筛选出拟合结果最优的Copula函数。BIC准则、RMSE准则和AIC准则数值越小,则雨、潮联合分布模型效果越优,从表4可以看出,拟合结果最优Copula函数为G-H Copula函数。

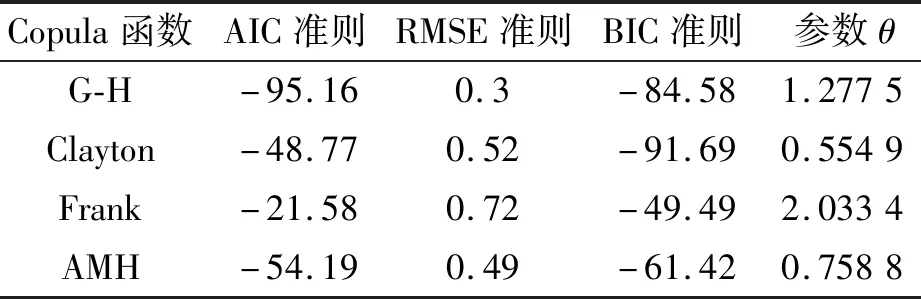
表4 4种候选Copula函数参数估计与拟合检验结果Tab.4 Parameter estimation and fitting test results of four candidate Copula functions

因此,G-H Copula函数构建北海站降雨量对应石头埠潮位联合分布模型如下

CGH=exp{-[(-lnu)1.277 5+(-lnv)1.277 5]1/1.277 5}

(10)

综上所述,雨、潮组合的联合分布模型如图1。

图1 雨、潮联合概率分布模型Fig.1 Joint probability distribution model of rainfall and tidal level

2.2 不同重现期特征分析

如图2中T分别为100 a、50 a、20 a、10 a和5 a的OR和AND重现期等值线所示,重现期等值线与45°线呈对称分布;这表明雨量和潮位可能对工程的设计水平计算具有相同的影响。然而,在实际工程中,雨量和潮位对工程的设计水平计算影响却不尽相同。因此,虽然图2在一定程度上显示了雨量与潮位的相关性,但未能考虑雨、潮组合与工程调洪的耦合关系。

2-a AND重现期等值线图 2-b OR重现期等值线图图2 重现期等值线图Fig.2 Contour calculation results of design periods

如图3的防洪重现期等值线所示,防洪重现期等值线上尾部分的斜率绝对值小于1,说明当雨量较大,潮位较低时,此时对明渠而言雨量起主要作用;随着雨量逐渐减小,潮位不断升高,防洪重现期等值线斜率绝对值逐渐大于1,说明此时潮位对调洪起主要作用,雨量的影响相对较小。

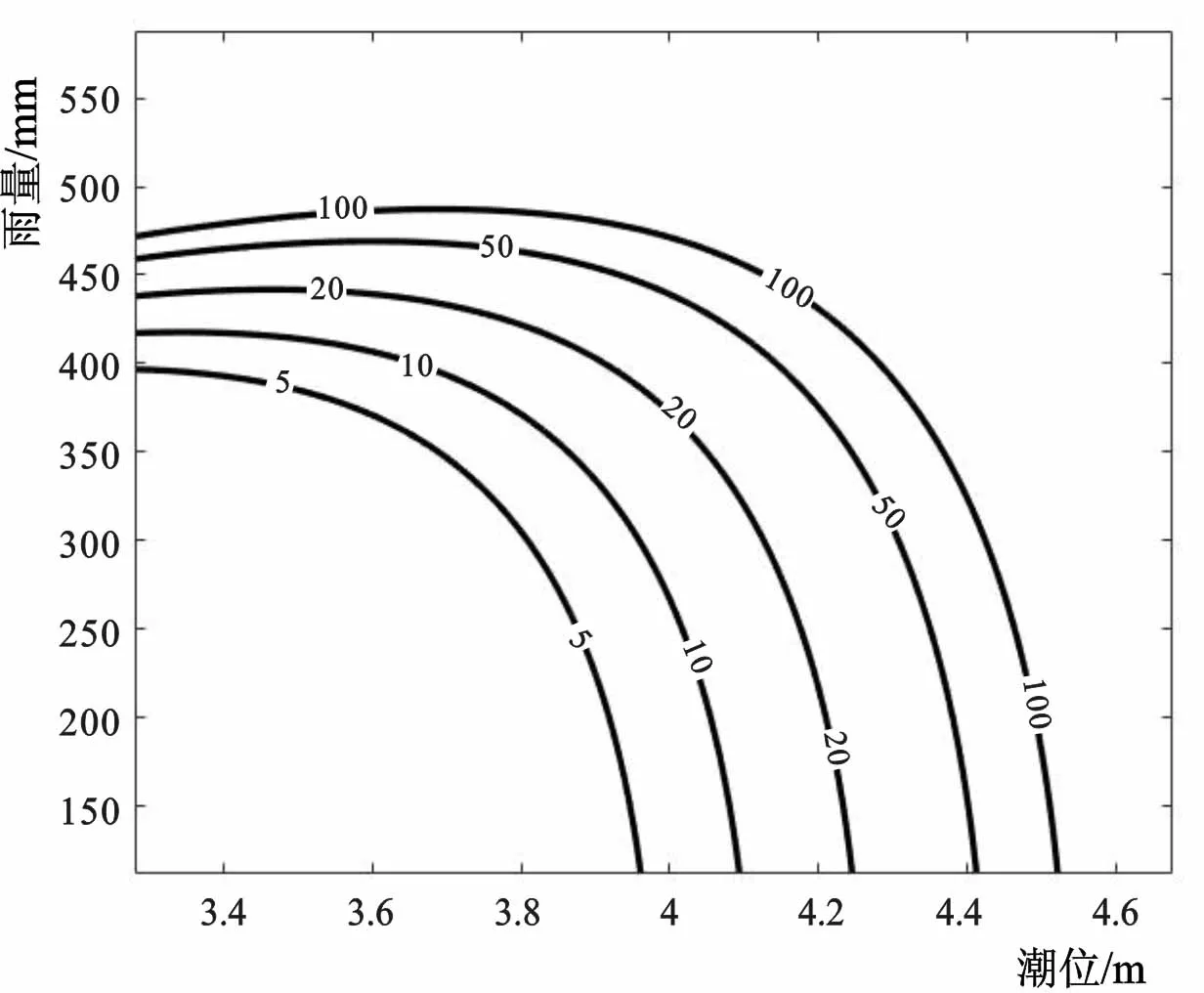
图3 防洪重现期等值线图Fig.3 Contour calculation results of flood control return period

图4描述了OR、AND和防洪重现期为20 a一遇的设计情况。图4中防洪重现期选取的是断面K7+340,按照防洪重现期计算其设计水深为4.02 m。通过对比发现,防洪重现期等值线处于OR、AND重现期等值线之间。常用的明渠水面线计算方法有均匀流法[11]、非均匀流法[12]和数值模拟方法[13-14]等,本文采用明渠非均匀流法,图5将防洪重现期20 a一遇水面线与OR、AND重现期20 a一遇水面线进行对比发现,防洪重现期20 a一遇设计水面线也处于OR、AND重现期之间,其中OR重现期对应的水面线比防洪重现期对应的水面线高约0.20 m,而AND重现期对应的水面线则要低约0.22 m,这表明防洪重现期可以避免出现OR、AND重现期设计结果偏高或偏低的问题,能有效提高工程防洪、防潮设计水平。

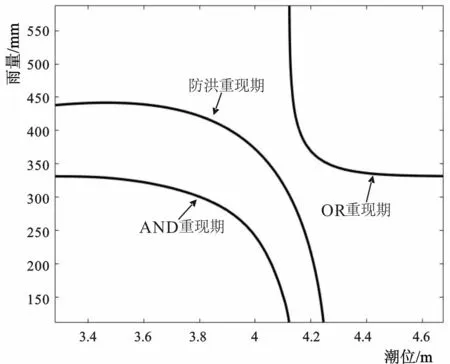
图4 三种设计重现期20 a一遇等值线图Fig.4 Contour calculation results of the recurrence period of 20 years of three designs

图5 三种设计重现期20 a一遇设计水面线计算成果图Fig.5 Calculation results of the design water surface line with the recurrence period of 20 years of three designs

2.3 雨、潮不确定性分析

SERINALDIF[15]采用小于样本容量长度的OR重现期分析两变量设计值不确定性问题。因此本文以小于实测样本序列(42 a)的10 a、20 a OR重现期作为分析对象,基于实测数据建立的联合分布模型为总体,分别设置样本容量n=42、n=100、n=200分析不同重现期下序列长度对联合设计值的影响。

联合分布的不确定性是由于参数的不确定性引起的。表5给出基于蒙特卡罗法不同样本容量条件下重现期为20 a,联合分布参数在95%水平下的置信区间。可以看出,参数的变幅随着样本容量的增加而不断减小。

表5 不同样本容量联合分布参数95%置信区间Tab.5 95% Confidence interval of joint distribution parameters of different sample size

如图6所示,同一OR重现期水平条件下,样本容量的增加导致最可能组合联合设计值95%置信区间逐渐减小。在同一样本容量n下,联合设计值二元置信区间随着OR重现期水平的增加而增大。此外,在T=20和n=42时,联合设计值最可能组合主要分布在T=5到T=100曲线之间。相反,在T=10和n=200时,联合设计值最可能组合主要集中在T=5和T=20曲线之间。这些结果表明,当样本容量n较小且设计重现期水平较大时,雨、潮联合设计值的不确定性也更大。

6-a n=42,TOR=10 6-b n=42,TOR=20 6-c n=100,TOR=10

采用本文1.3节所介绍的4个不确定性评价指标(DX、DY、S、d)对雨、潮组合不确定性进行了评估,由表6可知,DX、DY随着样本数量n增加而减小;当T=10 a时,d和95%置信区间的面积S分别减小38.9%、29.1%、38.3%和27.1%,在T=20 a时,分别减少59.9%、49.0%、54.5%和52.8%。

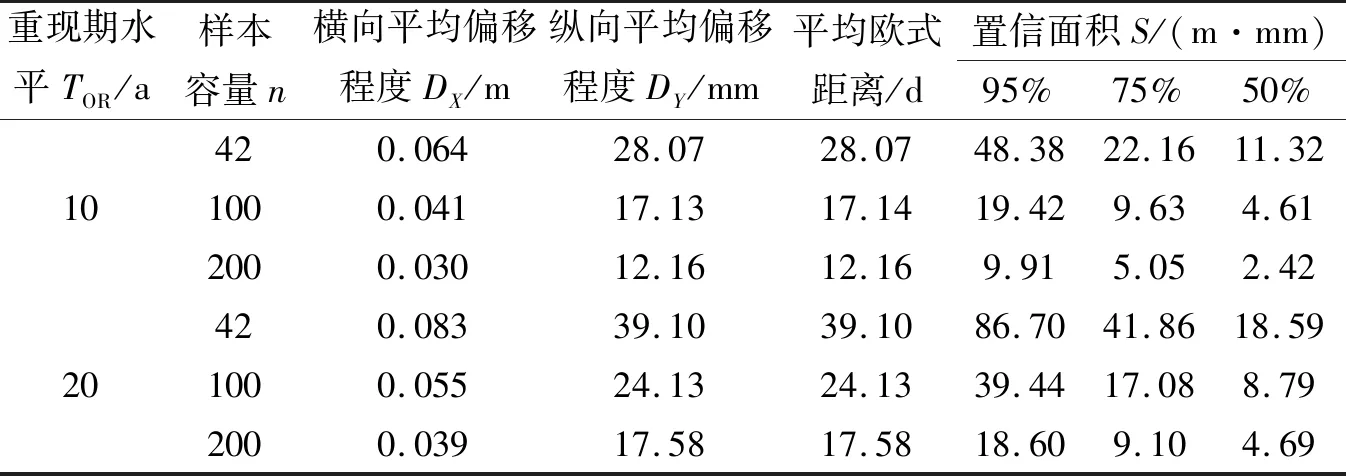
表6 OR重现期设计值不确定性评价指标计算结果Tab.6 Calculating results of uncertainty evaluation index of OR design period

2.4 设计水深不确定性分析

对于明渠的防洪安全而言,最主要的因素是设计水深,因此联合设计雨、潮组合的不确定性问题就转化为单变量的不确定性问题,即设计水深的不确定性,根据调洪规则可分别得到每一组参数下OR重现期最可能组合对应的N个设计水深以及防洪重现期标准下的设计水深。表7给出了不同重现期标准下明渠K7+340处设计水深的计算结果,可以看出在不同样本容量下,以防洪重现期为设计标准推求得到的20 a一遇设计水深的95%置信区间宽度和标准差均小于OR重现期,例如在雨、潮组合序列长度为实测序列长度(42 a)时,防洪重现期比OR重现期标准差偏小14.3%,区间宽度偏小21.4%,这说明了以防洪重现期为设计标准可减少设计水深的不确定性。

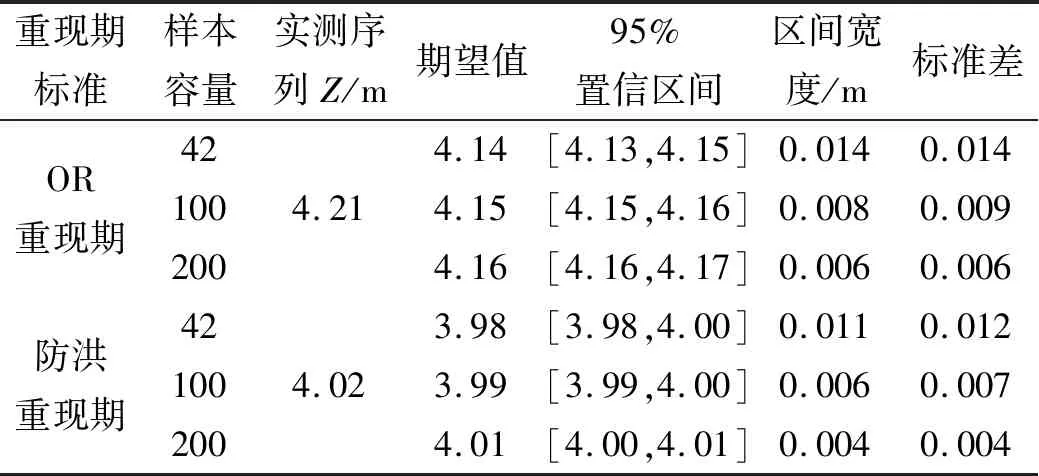
表7 不同重现期标准下明渠设计水深估计结果Tab.7 Estimation results of open channel design water depth under different return period standards

从表7还可以看出,当样本容量小于100时,两种重现期标准下的设计水深95%置信区间宽度均超过了10 mm,标准差均超过了0.01,也就是说当雨、潮样本序列长度较短时,设计水深估计结果在数值上波动性较大,会给明渠的设计水深带来较大的不确定性。因此,在实际工程中,有必要延长雨、潮序列使得设计结果更加可靠。

3 结论

以雨、潮联合作用下的铁山港入海明渠为研究对象,采用Copula函数构建两种重现期风险模型分析雨、潮遭遇及组合规律,并针对实际工程所采用的设计方法对雨、潮变量间的相关性考虑不足情况,提出了一种考虑雨、潮与工程调洪耦合关系的防洪重现期,并将该重现期与较为常见的两种二变量重现期进行对比分析,最后基于蒙特卡罗法分析抽样不确定性对于雨、潮共同作用下明渠设计水深的影响,得出以下结论：(1)与OR、AND重现期相比,防洪重现期可以有效避免最可能设计组合值设计标准偏高或偏低的情况;(2)在雨、潮联合作用下,最可能组合联合设计值95%置信区间随着重现期水平的递增而逐渐增加,随着样本容量的增加而逐渐减小;(3)明渠水深的不确定性和重现期的选取有关,防洪重现期与传统的OR重现期相比更能有效减少明渠设计水深的不确定性。