类场矩诱导的可调零场自旋转移力矩纳米振荡器*

郭晓庆 王强 薛海斌†

1) (太原理工大学物理学院,太原 030024)

2) (太原理工大学,新材料界面科学与工程教育部重点实验室,太原 030024)

3) (太原师范学院物理系,晋中 030619)

自旋转移力矩纳米振荡器是一种直流驱动的新型纳米微波振荡器,因其易集成、尺寸小、频率调制范围宽等优点,成为未来射频收发器的理想器件.但是,自旋转移力矩纳米振荡器的稳定自激振荡需要外加磁场的条件限制了其应用.基于宏自旋模型(又称单自旋或单畴模型),利用Landau-Lifshitz-Gilbert-Slonczewski 方程,理论上研究了类场矩和电流强度对垂直磁化的自由层磁矩的零场稳定自激振荡特性的影响.研究结果表明,当类场矩参数与自旋转移力矩参数的比值为负值且其绝对值大于某一数值时,自旋转移力矩纳米振荡器可以实现零场自激振荡,其物理机制可以通过能量平衡方程解释,并且这一临界比值依赖于该系统的阻尼系数和电流强度.尤其是,自旋转移力矩纳米振荡器的稳定自激振荡频率可以通过类场矩参数与自旋转移力矩参数的比值和电流强度的大小来调节,并且其类场矩的绝对值越大,施加的电流强度越小(大于临界电流强度),则越有利于抑制二次和三次自激振荡频率的形成,从而提高自旋转移力矩纳米振荡器的“单频”性.上述结果提供了一种实现频率可调的零场自旋转移力矩纳米振荡器的理论方案.

1 引言

磁性隧道结中的自旋转移力矩效应[1,2]和隧道磁电阻效应[3−5]提供了一种在纳米磁性系统中产生微波振荡的新方法,并导致一种新型微波振荡器件,即自旋转移力矩纳米振荡器的产生和发展[6−11].尤其是,自旋转移力矩纳米振荡器与传统的半导体微波振荡器相比,具有结构简单、尺寸小、低功耗、振荡频率调制范围宽,以及与互补金属氧化物半导体(complementary metal oxide semiconductor,CMOS)工艺完全兼容等特点,因而,其成为未来射频收发器的理想器件[12].目前,对于基于磁矩垂直磁化的FeB 自由层和磁矩面内磁化的CoFeB 固定层组成的MgO 磁性隧道结,已在实验上实现了输出功率为0.55 µW,频率为6.3 GHz,Q因子为135的微波信号[10].但是,在上面的FeB/MgO/CoFeB磁性隧道结,自由层磁矩的稳定自激振荡需要施加一个与膜面垂直的磁场[13−15],从而限制了其应用.因此,如何实现零场的自旋转移力矩纳米振荡器成为人们关注的重点研究领域之一.

在理论上,要实现自旋转移力矩纳米振荡器的零场稳定自激振荡,就需要引入新的物理效应,例如类场矩[16−18]、层间交换耦合作用[19]、二阶磁各向异性[20−23]以及面内形状各向异性[24−27].这些效应的共同特点是可以产生一个等效的磁场,因而,可以使其产生稳定的自激振荡.其中,对于引入类场矩的情形,理论研究已经证明类场矩参数与自旋转移力矩参数的比值为负值时,自由层的磁矩可以产生稳定的自激振荡[16−18].但是,对于该比值为负值时,自由层磁矩是否一定能产生稳定自激振荡;若不能,其产生稳定自激振荡的条件与哪些因素相关,均尚未被揭示.另外,如何调节自由层磁矩的稳定自激振荡频率,以及如何抑制自由层磁矩在稳定自激振荡中产生的二次和三次振荡频率,都依然是开放的问题.

本文理论上研究了类场矩对垂直膜面磁化的自由层磁矩的零场稳定自激振荡特性的影响,固定层的磁矩沿膜面,即平行于膜面磁化.研究结果表明,只有当类场矩参数与自旋转移力矩参数的比值为负值,且其绝对值大于某一数值时,自由层的磁矩才可以实现稳定的零场自激振荡,并且这一临界比值依赖于该系统的阻尼系数和施加的电流强度.当阻尼系数增大时,随着类场矩参数与自旋转移力矩参数的比值和电流强度的变化,自由层磁矩稳定自激振荡的区域在逐渐减小.此外,对于自由层磁矩可以产生稳定自激振荡的情形,类场矩参数与自旋转移力矩参数的比值的绝对值越大,施加的电流强度越小(大于临界电流强度),越有利于抑制二次和三次自激振荡频率的形成,从而提高自旋转移力矩纳米振荡器的“单频”性.上述结果可以为频率可调的零场自旋转移力矩纳米振荡器的实现提供理论指导.

2 理论模型

本文考虑的自旋转移力矩纳米振荡器由三个圆形薄膜组成,其结构示意图如图1 所示,最上面和最下面分别为磁矩垂直于圆形膜面的自由层和磁矩平行于圆形膜面的固定层,其单位磁矩分别用m和mP表示;中间为隧道势垒层,其由1 nm 厚度的非磁性材料形成.这里,自由层的厚度d和截面半径r分别选取为2 nm 和60 nm;并选取x-y平面平行于膜面,z轴垂直于膜面向上,相应地,自由层的易磁化轴沿着z轴方向,固定层的磁矩沿着x轴的正方向.此外,在球坐标系中,φ和θ分别为自由层磁矩m的方位角和极角.

图1 由三个圆形薄膜组成的自旋转移力矩纳米振荡器的示意图.该结构上面为厚度d 和截面半径r 分别为2 nm 和60 nm 的自由层,且其磁 矩垂直于膜面;中间为1 nm 厚度非磁性材料形成的隧道势垒层;下面为磁矩平行于膜面的极化层.在笛卡尔坐标系中,x-y 平面和z 轴分别平行和垂直于膜面,而在球坐标系中 φ 和θ 分别为自由层磁矩的方位角和极角Fig.1.Schematic diagram for the considered spin-transfer torque nano-oscillator consisting of the trilayer circular thin films.Here,the top,middle and bottom layers are the 2 nm-thick perpendicular magnetized free layer with a radius of 60 nm,the 1 nm-thick tunnel barrier layer formed by non-magnetic material and the in-plane polarizer pinned layer,respectively.Moreover,in the Cartesian coordinate system,the x-y plane and z-axes of are parallel and perpendicular to the free layer,respectively;while the φ and θ in the spherical coordinate system are the azimuth and polar angles of the magnetization of the free layer,respectively.

自由层的磁矩动力学方程通过Landau-Lifshitz-Gilbert-Slonczewski (LLGS)方程描述[1,28,29]:

其中γ是旋磁比;Heff是自由层受到的有效场;α是Gilbert 阻尼系数;HS是自旋转移力矩参数,其数值依赖于自由层磁矩m与固定层磁矩mP之间的夹角,这也是自由层磁矩m能产生稳定振荡的重要因素,其表达式可以写为[16−18,20]

其中 ℏ 为约化普朗克常数;η为自旋极化率;I为施加的电流强度;e为电子的电量;Ms为饱和磁化强度;V=Sd(S=πr2为自由层膜面的截面面积)为自由层体积;λ为无量纲的参数,其大小与自由层磁矩和固定层磁矩有关.需要特别说明的是,(1)式右边的第四项即为本文重点考虑的类场矩项,其中β是类场矩参数与自旋转移力矩参数的比值.另外,为讨论方便,自旋转移力矩纳米振荡器的膜面形状选取为圆形,并且自由层为单轴各向异性的磁性材料.此时,自由层的面内形状各向异性场为0,仅剩垂直膜面的形状各向异性场,即退磁场:

其中µ0表示真空磁导率;而自由层的磁晶各向异性场可以表示为[18]

相应地,自由层磁矩受到的有效磁场为

其可以进一步写为

为求解磁矩m的动力学问题,将(1)式两边同时左叉乘磁矩m,可得

其中Γ=(1+α2)/γ.由(5)式可知,在笛卡尔坐标 系下,磁矩m的三个分量mx,my和mz遵循的运动方程可表示为

其中Heff,i表示自由层磁矩受到的有效磁场Heff在i轴方向的分量.这里,自由层磁矩mx,my和mz三个分量的动力学可以通过四阶Runge-Kutta 方法数值求解上面的三个关联方程获得.

3 结果与讨论

在下面的数值计算中,自旋转移力矩纳米振荡器的相关参数[16−18,22]选取为: 阻尼系数α=0.005(除非特殊说明),旋磁比γ= 1 .761×1011A·s·kg-1,饱和磁化强度Ms=(4π)-1× 1 .82×107A/m ,固定层极化率η=0.54 ,无量纲参数λ=η2,自由层圆形薄膜的厚度和半径分别为d=2×10-9m 和r=60×10-9m ,自由层的界面垂直各向异性场和退磁场分别为µ0Hk=1.86 T 和µ0Hd=1.68 T .

3.1 零场振荡条件

对于本文考虑的自旋转移力矩纳米振荡器,其固定层的磁矩沿着x轴的正方向,由巨磁阻效应可知,器件的电阻变化与自由层磁矩x轴分量的大小变化相关.因而,对于一个可以通过磁输运实验探测的稳定进动磁矩,其x轴分量mx相对其平均值的均方根:

(7)式可以用来判断其磁矩能否产生稳定的自激振荡,其中mxi是时间序列中磁矩x轴分量mx的第 i 个值,是其相应的平均值.当mx-rms≠0 时,自由层磁矩m能够产生稳定自激振荡[30].为了研究类场矩对自旋转移力矩纳米振荡器零场振荡条件的影响.图2 给出了自由层磁矩稳定自激振荡在不同阻尼系数情形下随类场矩参数与自旋转移力矩参数比值β和电流强度I变化的相图.当β≥0时,自由层的磁矩将趋向于固定层磁矩mP的反方向,最后停留在 -mP方向[16].尤其是,对于给定的阻尼系数α,当β＜0 且其绝对值|β| 较小时,自由层磁矩依然不能产生稳定的自激振荡,并且该 |β|的最小临界值随着电流强度增大而逐渐增大,如图2 相图右侧的分界线所示.

图2 自由层磁矩 x 轴分量 mx 的均方根 mx-rms 在不同阻尼系数下随β 和I 变化的相图 (a) α=0.003 ;(b) α=0.005 ;(c) α=0.007 ;(d) α=0.009Fig.2.Phase diagrams of the root-mean-square value of mx-rms of the mx component of the free layer as a function of β and I with different Gilbert damping constants: (a) α=0.003 ;(b) α=0.005 ;(c) α=0.007 ;(d) α=0.009 .

事实上,仅当β＜0 且其绝对值|β| 大于 某一临界值时,自由层磁矩才能产生稳定的自激振荡,如图2 所示.但是,当β＜0 且其绝对值|β| 足够大时,自由层磁矩的稳定自激振荡将消失,但是该 |β|的最大临界值随着电流强度增大而逐渐减小,如图2相图左侧的分界线所示.因此,对于β＜0 的情形,仅是自由层磁矩产生稳定振荡的必要条件.另外,系统的阻尼系数α与施加的电流强度I一样,同样会影响 |β| 的临界值.例如,对于给定的电流强度,随着阻尼系数α的增大,能够使自由层磁矩产生稳定自激振荡的 |β| 值范围在逐渐减小,如图2 所示.

为了分析磁矩稳定自激振荡的物理机制.下面,考虑磁矩产生稳定自激振荡的条件.在一个进动周期内,自旋转移力矩纳米振荡器的系统总能量E对时间的变化率可表示为

其中Heff,total表示系统受到的总有效场.由于(1)式可重新写为

因此,考虑类场矩情形时,系统的总有效场表示为Heff,total=Heff+βHSmP.相应地,在一个周期的振荡过程中,自旋转移力矩做功提供的能量Ws和阻尼导致的能量耗散Wα可分别表示为[13,17,22,24,31−33]:

在理想情形下,自旋转移力矩纳米振荡器产生稳定的振荡时,其磁矩将沿着固定的倾角θ转动.这里,θ表示磁矩与垂直膜面方向z轴的夹角.因此,磁矩进动一个周期,其能量对时间变化率的平均值可表示为

此时,在一个进动周期内,自旋转移力矩做功提供的平均能量和阻尼导致的平均能量耗散可分别表示为[17]

图3 给出了在一个进动周期内自旋转移力矩提供的平均能量,阻尼导致的平均能量耗散,以及其平均能量之差随自由层磁矩z分量的变化.当β=0 时,对于施加的电流强度大于其临界值的情形,自旋转移力矩提供的能量总是能克服阻尼力矩导致的损耗,使自由层磁矩从mz=1翻转到mz=0 ,从而导致磁矩不能产生自激振荡.当β＞0 时,类场矩实际上可以等效为一个沿着固定层磁矩mP方向的磁场,他将使磁矩进动轨迹的轴线偏离z轴,向x轴靠近.此时,自旋转移力矩提供的能量总是大于阻尼导致的能量耗散,因而,磁矩快速地趋向于 -mP的方向.对于β＜0 的情形,类场矩则等效为一个沿着固定层磁矩mP反方向的磁场,它将使磁矩进动轨迹的轴线偏离z轴,向x轴的负方向靠近.相应地,自旋转移力矩提供的能量减少,从而使其与阻尼导致的能量耗散平衡.因而,可以实现磁矩的稳定自激振荡.

图3 当电流为1.5 mA 时,在一个周期内,自旋转移力矩提供的平均能量 ,阻尼消耗的平均能量 ,以及其平均能量之差-随自由层磁矩z 分量的变化 (a) β =0;(b) β =–0.2;(c) β =0.2Fig.3.In a precession period,the average work done by the spin-transfer torque ,the average energy dissipation due to the damping ,and the energy difference between and as a function of the z component of the free layer magnetization at given current intensity I=1.5 Ma: (a) β =0;(b) β =–0.2;(c) β =0.2.

另外,由于磁矩稳定自激振荡轨迹的轴线实际上偏离z轴,向x轴的负方向靠近,因而,磁矩z分量的数值在一个稳定自激振荡周期内同样是周期性变化的.需要说明的是,在推导磁矩稳定自激振荡的条件时,假设磁矩与z轴的夹角θ不变,因而,在定量上,(12a)式和(12b)式确定的磁矩稳定自激振荡条件与数值模拟结果之间有一定的偏差,尤其是对于β值足够大时的情形.

3.2 类场矩对零场自激振荡频率和振幅(功率)的影响

首先讨论自旋转移力矩纳米振荡器在理想情形下产生稳定振荡的频率.在球坐标下,决定自由层磁矩含时演化的LLGS 方程可以表示为

当自由层的磁矩m产生稳定振荡时,其磁矩m与z轴的夹角θ保持不变,则有 dθ/dt=0 ,由(13a)式可得自旋转移力矩参数HS有如下形式:

然后,将上面的(14)式代入(13b)式可得

自由层磁矩的一个进动周期可以表示为

将(15)式代入上面的(16)式可得

因而,在理想情形下,自旋转移力矩纳米振荡器产生稳定振荡的频率可以表示为

由(18)式代入上面的(16)式可得,自旋转移力矩纳米振荡器产生稳定振荡的频率依赖于其稳定振荡时自由层磁矩m与z轴的夹角θ和类场矩参数与自旋转移力矩参数的比值β.下面分别讨论类场矩参数与自旋转移力矩参数的比值β,以及施加的电流强度I对自旋转移力矩纳米振荡器稳定振荡频率和振幅的影响.

对于本文考虑的自旋转移力矩纳米振荡器,其固定层的磁矩mP沿着x轴的方向,因而要研究类场矩参数β对自旋转移力矩纳米振荡器稳定振荡频率的影响,就需要对时域的自由层磁矩x轴分量mx(t) 做分离傅里叶变换,将其变换到频域mx(f).其中,磁矩稳定自激振荡的功率定义为I2·df[10].为准确给出磁矩稳定自激振荡的频率性质,mx(t)的数据选取其产生稳定振荡之后的时间区域.对于给定的电流强度I=1.5 mA ,图4 给出了磁矩在稳定自激振荡情形下,其频率和振幅对类场矩参数与自旋转移力矩参数的比值β的依赖关系.这里,需要说明的是,当磁矩产生稳定的自激振荡时,将其z轴分量mz(t)的 最大值mz,max和最小值mz,min分别作为 c osθ和相应的类场矩参数与自旋转移力矩参数的比值β代入(18)式,得到的磁矩自激振荡频率范围均包含数值结果给出的自激振荡频率,如图4(a)中第一个峰值对应的频率为1.54 GHz,在其解析频率1.29—1.80 GHz 范围内.对于磁矩可以产生稳定自激振荡的β范围,绝对值|β| 越大,其稳定自激振荡的频率就越大,如图4(a)中β=-0.6 的情形和图5(a)的相图所示.尤其是,其振幅mx(f)还可以保持一个较大的值,如图4(a)中β=-0.6 的情形和图5(b)的相图所示.另外,类场矩参数与自旋转移力矩参数比值的绝对值 |β|越大,其产生稳定自激振荡所需要的时间就越长,如图4(b)所示,并且其磁矩越趋向于z轴方向,即z轴分量mz(t)的 平均值m¯z就越大,如图4(c)所示.此外,对于磁矩在 |β| 绝对值较小情形下产生的稳定自激振荡,其二次自激振荡频率的振幅将非常明显,如图4(a)中β=-0.1 和β=-0.2 的情形,此性质将影响自旋转移力矩纳米振荡器的“单频”性.因此,当电流强度不变(大于临界电流强度)时,对于一个可以产生稳定自激振荡的负的类场矩参数,类场矩参数与自旋转移力矩参数的比值的绝对值 |β|越大,越有利于抑制二次自激振荡的形成.

图4 (a) 自旋转移力矩纳米振荡器的振幅和频率对β 的依赖关系;(b),(c) 自由层磁矩的x 分量和z 分量在不同类场矩β 情形下的稳态振荡情况(I=1.5 mA)Fig.4.(a) Dependences of the amplitude and frequency of spin-transfer torque nano-oscillator on the β;(b),(c) the x and the z components of the free layer magnetization as a function of time for the different ratios between the spintranfer torque and the field-like torque β (I=1.5 mA).

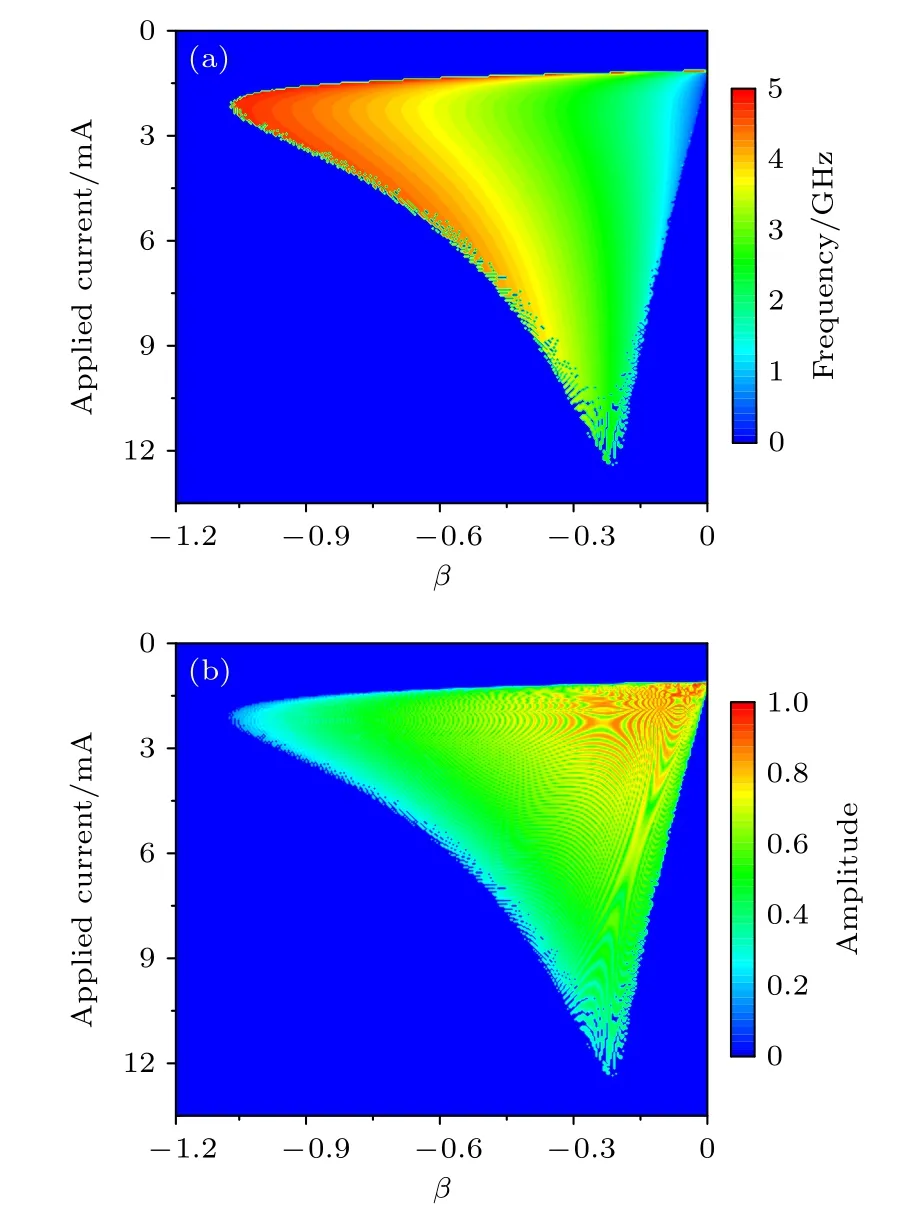
图5 α=0.005 时,自旋转移力矩纳米振荡器稳定自激振荡的频率(a)和振幅(b)随β 和I 变化的相图Fig.5.Phase diagrams of the frequency (a) and amplitude(b) of stable oscillation of spin-transfer torque nano-oscillator as a function of the β and the I at α=0.005.

另外,为提高自旋转移力矩纳米振荡器的输出功率,可以设计具有相互作用的自旋转移力矩纳米振荡器阵列[34−36],然后通过锁相同步技术[37−41],即使多个互联的自旋转移力矩纳米振荡器在同一偏置电流下产生同步自激振荡,或给自旋转移力矩纳米振荡器阵列施加相同的激励信号,使其发生同步自激振荡,从而将其自激振荡的相位与激励信号的相位锁定在一起.因而,通过锁相同步技术对自旋转移力矩纳米振荡器阵列的自激振荡相位的束缚,不仅可以减少振荡噪音,而且可以获得线宽更窄的优质微波信号.在理想情况下,对于N个互联并同步的自旋转移力矩纳米振荡器阵列,其输出功率为单个自旋转移力矩纳米振荡器的N2倍.

3.3 电流强度对零场自激振荡频率和幅值(功率)的影响

图6 给出了磁矩在稳定自激振荡情形下,施加的电流强度对其稳定自激振荡频率和振幅的影响.对于固定的类场矩参数,例如β=-0.2 ,随着施加的电流逐渐增大,磁矩稳定自激振荡的一阶频率有一个最小值,如图6(a)所示,并且该频率的最小值随着β绝对值的越大而增大,如图5(a)的相图所示.但是,随着电流强度的增大,例如,I=4.0 mA ,磁矩稳定自激振荡的二次,甚至三次频率对应的幅值将变得非常明显,如图6(a)所示.因而,为了提高自旋转移力矩纳米振荡器的“单频”性,对于一个可以产生稳定自激振荡的负的类场矩参数,其施加的电流强度较小(大于临界电流强度)时,将有利于抑制二次和三次自激振荡频率的形成,并且此时不仅稳定自激振荡的频率会相应增大,而且其振幅mx(f)也有一个较大的值,如图5(b)的相图所示.另外,施加的电流强度越大,磁矩产生稳定自激振荡所需的时间越短,如图6(b)所示.此外,由图6(c)可知,对于磁矩可以产生稳定自激振荡的电流强度范围,电流强度的值越大,磁矩在一个稳定自激振荡周期内的z轴分量mz(t)的变化范围就越大.相应地,磁矩进动轨迹的轴线越趋近于x轴方向.

图6 (a)自旋转移力矩纳米振荡器的振幅和频率对施加电流强度I 的依赖关系;(b),(c) 自由层磁矩的x 分量和z 分量在不同电流强度情形下的稳态振荡情况(β =–0.2)Fig.6.(a) Dependences of the amplitude and frequency of spin-transfer torque nano-oscillator on the applied current intensity I;(b),(c) the x and the z components of the free layer magnetization as a function of time for the different values of current intensity (β =–0.2).

4 结论

基于LLGS 方程,研究了自旋转移力矩纳米振荡器的自由层类场矩和外加电流强度对其磁矩稳定自激振荡特性的影响.数值结果表明,当自由层的类场矩参数与自旋转移力矩参数的比值为负值,且其绝对值大于某一数值时,自旋转移力矩纳米振荡器可以实现零场自激振荡,其物理机制可以通过能量平衡方程解释.尤其是,自旋转移力矩纳米振荡器的稳定自激振荡频率,可以通过类场矩参数与自旋转移力矩参数的比值和施加的电流强度来调节.例如,对于一个可以产生稳定自激振荡的负类场矩参数,类场矩参数与自旋转移力矩参数比值的绝对值越大,稳定自激振荡的频率也越大,并且对于二次、三次自激振荡频率的抑制也更有利,从而可以提高自旋转移力矩纳米振荡器的“单频”性.另外,对于一个确定的可以产生稳定自激振荡的负类场矩参数,施加的电流强度越小(大于临界电流强度),其自激振荡的频率反而越大,并且更有利于抑制二次和三次自激振荡频率的形成.上述结果为频率可调的零场自旋转移力矩纳米振荡器的实现提供了一种可选择的理论方案.