基于半监督学习和稀疏表示的质谱仪运行灵敏度故障检测算法

韦怡

摘 要： 为了解决质谱仪运行灵敏度故障对环境监测和化学污染监测产生的影响，提高监测数据的准确性和可靠性，提出了一种基于半监督学习和稀疏表示研究质谱仪运行灵敏度故障检测算法。根据半监督学习的原理对质谱仪的运行数据进行划分，在混合数据中标记运行灵敏度的故障特征。通过对应特征处理原始数据，在去噪和归一化特征的基础上求取灵敏度系数。采用稀疏表示理论对系数转换，以约束范数关系建立故障监测目标函数，检测质谱仪运行灵敏度故障。结果表明：以3种类型运行灵敏度故障作为测试对象，新算法可以实现较高精度的故障检测，且不受样本数量的限制，具有一定的应用价值。

关键词： 半监督学习；稀疏表示；质谱仪；故障检测

中图分类号： TP181；TQ110.9

文献标志码： A  文章编号： 1001-5922（2023）08-0142-04

A fault detection algorithm for running sensitivity of mass Spectrometer  based on semi-supervised learning and sparse representation

WEI Yi

（Jiangxi University of Technology，Nanchang 332020，China）

Abstract： In order to solve the impact of mass spectrometer operating sensitivity failure on environmental monitoring and chemical pollution monitoring，and improve the accuracy and reliability of monitoring data，a fault detection algorithm for mass spectrometer operating sensitivity based on semi supervised learning and sparse representation is proposed.According to the principle of semi supervised learning，the operation data of mass spectrometer was divided，and the fault characteristics of operation sensitivity were marked in the mixed data.By processing the raw data with corresponding features，the sensitivity coefficient was calculated based on denoising and normalization features.Using sparse representation theory to transform coefficients，a fault monitoring objective function was established based on constrained norm relationships to detect sensitivity faults in mass spectrometer operation.The experimental results showed that the new algorithm could achieve high-precision fault detection with three types of sensitivity faults as test objects，and was not limited by the number of samples，which had certain application value.

Key words： semi-supervised learning;sparse representation;mass spectrometer;fault detection

质谱仪运行灵敏度故障会对环境监测和化学污染监测造成负面影响，例如检测精度下降、数据处理出错和监测范围缩小等[1-2]。因此，需要及时发现和解决质谱仪运行灵敏度故障问题，以确保监测数据的准确性和可靠性，为环境保护和公共安全等领域提供技术支持。。

为实现质谱仪的有效应用，如在文献[3]中，为排除Isoprime 100稳定性同位素比质谱仪检测过程中的常见故障，结合实际操作对仪器进行全方位分析，并且设计了一个故障排除方法。从仪器应用前以及应用过程进行分析，对漏检、峰值错检以及稳定性不达标等问题进行预设，对数据中的重点信息进行提取和标定，在保证数据准确性的基础上判断质谱仪的运行稳定性，以此实现质谱仪的高效应用。随着电感耦合等离子体质谱仪的广泛应用在文献[4]中，主要针对电感耦合等离子体质谱仪进行研究，对质谱仪的使用方法进行设定，并根据影响仪器的参数设计了故障检测方法。该检测方法主要针对质谱仪中自带的Synigistix Version 1.1软件，对其常见的问题进行分析，通过举例说明各相运行故障的解决方法，为故障的及时排查提供了参考依据。无论是哪一种传统方法，均是对常见故障进行分析，为实现质谱仪的有效应用，采用半监督学习和稀疏表示技术，重新设计一个质谱仪运行灵敏度的故障检测算法，为其稳定運行提供技术支持。

1 基于半监督学习标记运行灵敏度故障特征

随着机器学习和识别技术的发展，半监督学习算法能够同时发挥有监督和无监督学习的优势，将其应用在质谱仪运行数据训练中，可以同时对海量样本进行标签设定，在质谱仪运行产生的不同数据样本中对数据进行无差别训练。在质谱仪运行过程中会产生大量的数据，将其作为运行灵敏度故障监测的训练集合，只需要对一部分故障特征进行标签设定，即可以通过半监督学习模型进行数据求解。不同的故障会产生具有特色的故障特征，为实现不同类型故障特征的划分，对样本标签进行给定[5]。假设随机样本为 q ，其真实的故障类型标签为 w∈e ，且 e= 1，2，…，r  ，则样本通过半监督学习模型生成后的特征成分为：

t q =∑ r y=1 β yt q α y∑ y     （1）

∑r y=1β y=1   （2）

式中： β y 為故障特征的混合系数[6]，且 β y≥0 ； t q α y∑ y   为给定样本 q 属于第 y 类故障特征成分的概率； α y 、 ∑ y 均为参数。在此基础上， 设定半监督学习模型对样本 q 的故障特征预设标记为 i q ∈e ，则最大化成分概率为：

i q = arg   max  o∈e t w=o q  = arg   max  o∈e ∑ r y=1 t w=o，y= Θ  q  =  arg   max  o∈e ∑ r y=1 t w=o y= Θ ，q  ×t y= Θ  q       （3）

式中：  Θ ∈ 1，2，…，r  为样本 q 对应的故障特征混合成分； t w=o y= Θ ，q   为样本 q 由第 y 类故障特征成分生成但属于 o 类型的概率。其中 t w=o q   可表示为：

t y= Θ  q  = β y×t q α y∑ y   ∑ r y=1 β yt q α y∑ y      （4）

式中： t y= Θ  q   为样本 q ，由第 y 类特征生成的后验概率[7]。通过式（3）、式（4）能够看出，对 t w=o y= Θ ，q   的估计需要知道样本的标签，但 t y= Θ  q   不需要样本标记，因此在半监督学习模型中对特征进行标记，需要对质谱仪的运行数据集进行分析，以此对数据进行预处理。

2 序列向前特征法求取质谱仪运行灵敏度系数

质谱仪在运行过程中其信号高度与噪声信号高度之间存在一定联系，一般情况下，噪声范围分布在质谱峰值后的0.5 s之后。根据图中内容可知，对信号噪声的处理与信号高度及平均噪声有关，因此采用基线噪声信噪比处理信号噪声：

p= a s    （5）

s=  ∑ d d=1  f-f -  2 d     （6）

式中： p 为信噪比； s 为噪声标准差； a 为质谱仪信号高度； f -  为基线噪声平均高度； f 为噪声高度； d 为信号强度。直接对数据的噪声进行去除，完毕后对样本数据的特征进行归一化处理，本文以序列向前特征选择方式构建特征子集。

由于质谱仪在运行过程中，横纵坐标表示内容具有差异性，其中横坐标一般表示离子的质量数，纵坐标表示采样强度，而图谱的信号峰值强度取决于质谱仪的灵敏度。在参数固定不变的条件下，物质成分的离子流强度与分压强度是成正比的，则：

g h∝j+ hg k∝j+ k      （7）

在常规质谱仪检测中待测的混合化合物会存在多种物质。本次以2组物质 h 、 k 为例，其中 g h 、 g k 表示分压强； j+ h 、  j+ k 为离子流强度[8]。对质谱仪的运行灵敏度计算，需要假定其中某一组物质不变，则求取过程：

l= g′ h/g′ k g h/g k = j′ h/j′ k j h/j k = 1+  1  x h  ×n h z  1+  1  x k  ×n k z     （8）

式中： l 为灵敏度系数[9]； g′ h 、 g′ k 、 j′ h  、 j′ k 分别为物质 h 、 k 提取后的分压强和离子流强度； x h 、 x k 为 h 、 k 的相对分子质量； z 为空间体积； n h 、 n k 为 h 、 k 的分解系数[10]。对质谱仪的运行灵敏度系数进行计算，能够实现对质谱仪自身应用过程中的性能分析，针对该系数采用稀疏表示理论进行转换，在字典转换矩阵中表示原始运行信号，实现故障检测。

3 稀疏表示理论检测质谱仪运行灵敏度故障

稀疏表示被应用于多个工程领域，具有高效的表达方式，将其应用在质谱仪运行灵敏度故障检测中，主要是将非稀疏的原始信号进行转换，将其标记为稀疏的系数。对于上文中求解的灵敏度系数，将其作为检测的原始信号，则其稀疏表示公式为：

l″=mφ   （9）

式中： l″ 为灵敏度系数的稀疏表示，具体为 l″= l″ 0，l″ 0，…，l″ Q  ，其中 Q 为长度[11]。 m 为字典矩阵，表示为 m= m 0，m 1，…，m W  ， m E 为列向量，又被称作字典原子，满足 ‖m E‖=1 。 φ 为稀疏解，表示为 φ= φ 0，φ 1，…，φ W  。综合各矩阵关系，对 l″ 的表示形式进行展开：

l″=∑ W E=1 φ Em E   （10）

当字典矩阵的长度为 Q=W 时为完备字典，不能满足稀疏表示的需求，因此采用稀疏表示时需要保证 Q<W ，即原子数要大于灵敏度系数的长度[12]。为此，采用范数对稀疏表示进行约束：

‖φ‖ R= ∑ W E=1  φ E R  1 R    （11）

式中： R 为约束范数。稀疏表示的目的是尽可能的还原灵敏度系数的原始信号，因此在以稀疏表示作为灵敏度故障检测时[13]，可以直接將检测结果表示为稀疏表示的目标，则故障检测的近似目标函数可表述为：

arg   max ‖φ‖ R，s.t.φm=l″   （12）

R 1= φ  1+ φ  2+ φ  3+…+ φ  WR 2= φ2 1+φ2 2+…+φ2 W      （13）

式中：以最大化约束范数  arg   max [KG-1mm]‖φ‖ R 作为灵敏度检测目标，在不同情况下采用不同的约束方式，此次选择 R 1 、 R 2  2种范数形式，当灵敏度系数的长度与求取距离等价时，采用 R 1 ；当灵敏度系数长度与其不等价时，采用 R 2 。至此，本文基于半监督学习和稀疏表示实现质谱仪运行灵敏度故障检测算法设计。

4 实验测试分析

4.1 测试数据准备

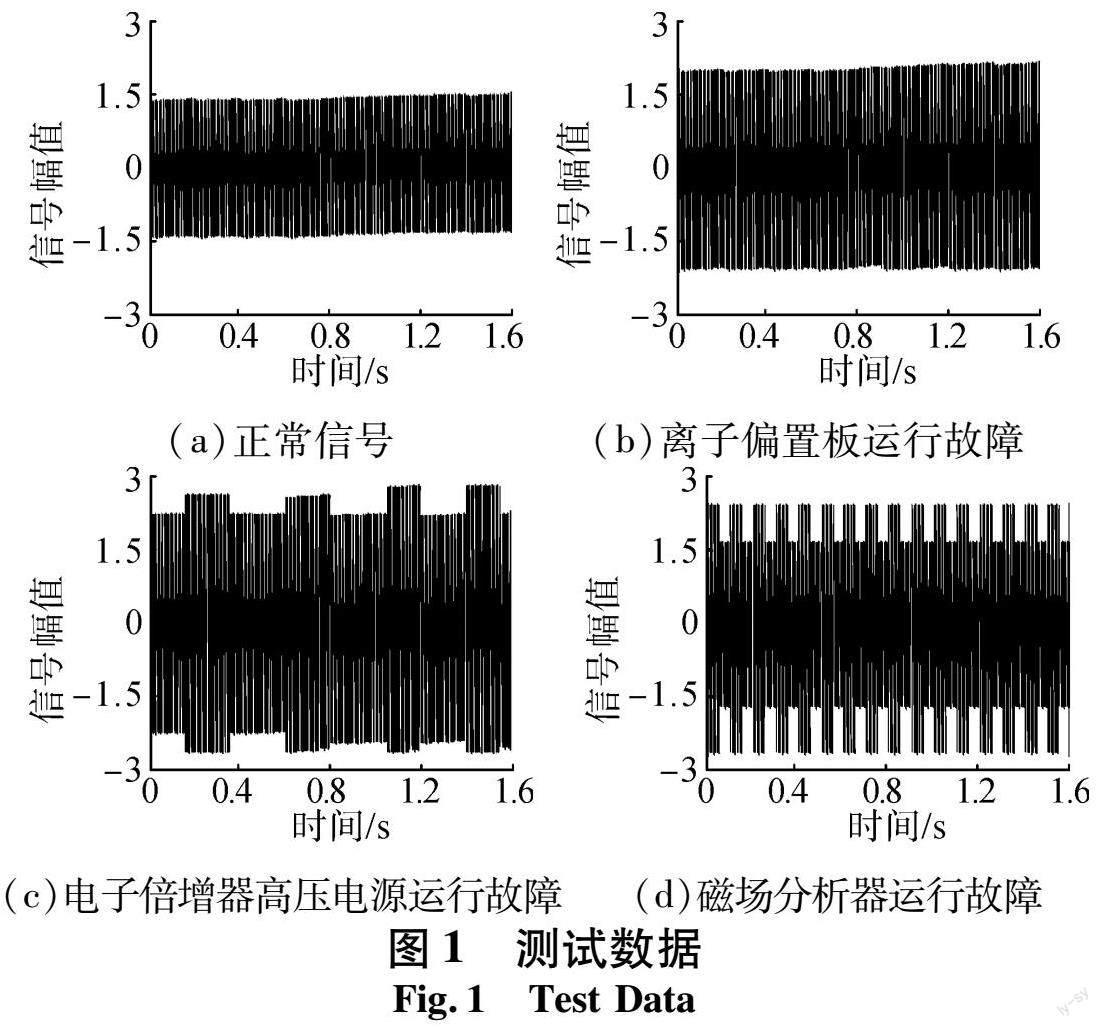
为验证各组算法对质谱仪运行灵敏度的故障检测效果，以实际应用的质谱仪作为测试对象，对其正常运行的信号和故障信号进行提取，其中正常信号作为故障信号的对照组，故障信号分为3组类型，分别为离子偏置板运行故障、电子倍增器高压电源运行故障、磁场分析器运行故障。对不同类型模式进行分析。

（1）离子偏置板运行故障： 该装置一般用来衡量信号的稳定性，常规运行下其信号输出为±1.5 V；

（2）电子倍增器高压电源运行故障：主要对输出电源进行控制，一般情况下信号需要控制在16位精度，本次设定输出为±2.0 V；

（3）磁场分析器运行故障：该装置是控制质谱仪的磁场分析强度，一般会持续运行，此次设定为±2.5 V。

根据上述设定情况，随机选择4组测试数据，具体情况如图1所示。

如图1（a）所示，在正常信号运行中其幅值在  －1.5，1.5  变动，且没有出现异常的峰值；在图1（b）中受离子偏置影响，质谱仪的运行幅值会发生调转，整体运行信号超过±1.5；图1（c）中则是突然出现幅值峰值，超过设定标准；图1（d）中受磁场波动性影响，在出现故障时其幅值达不到设定标准，且波动性较大。根据不同质谱仪运行灵敏度故障情况，将上述测试数据连接在MATLAB测试平台，分别通过3种方法进行检测。

4.2 测试结果分析

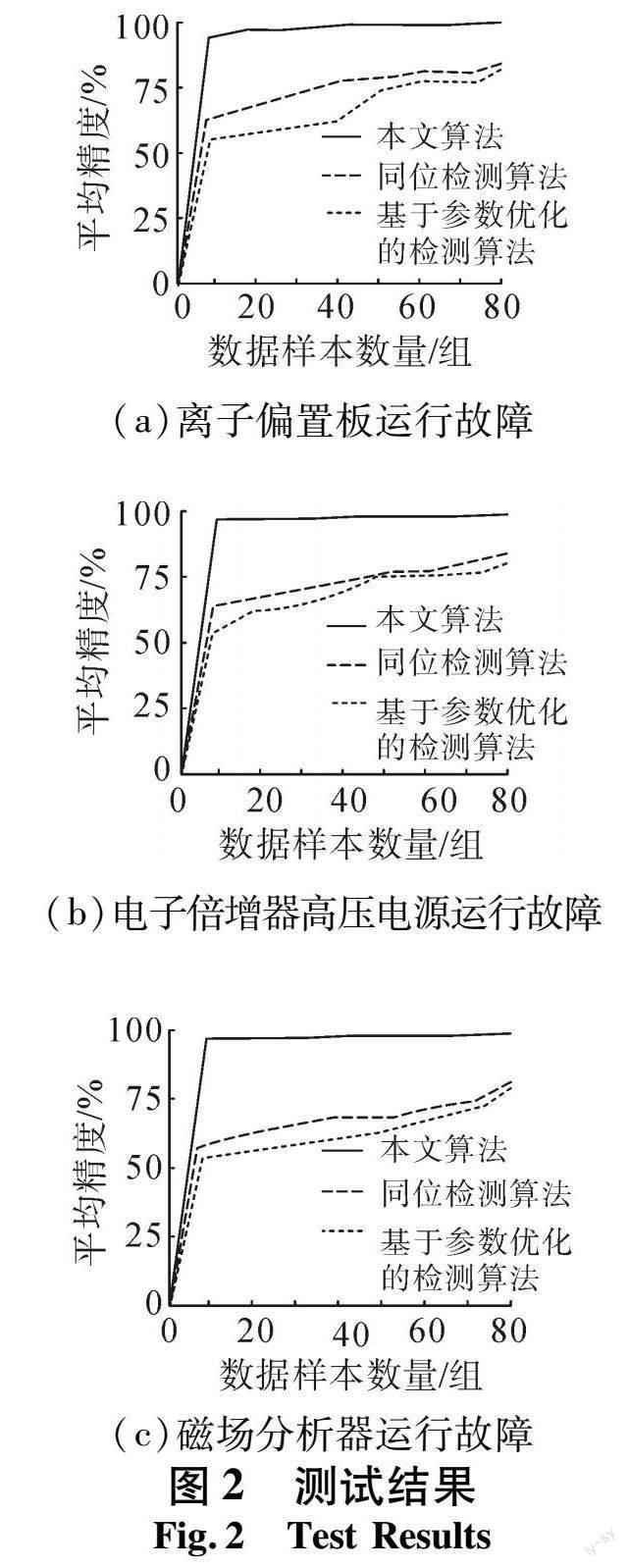
直接对一组数据样本检测无法证明各组方法的应用效果，通过选择的质谱仪故障类型，以小波技术对故障特征进行提取，并构造出240组测试数据集合，设定每类故障的数量相一致，均为80组。为避免单次测试的误差，对上述每一种故障类型的检测分别进行8次检测，以平均精度作为测试指标，计算方式为：

A - = ∑D S/F S S ×100%   （14）

式中： S 为测试次数； D S 为检测结果； F S 为实际故障类型。 A -  为平均精度。本次测试的样本变量为每一类故障的数量，当样本数量含量不同时得到的故障检测结果也会不同，一般情况下，样本数量越少检测的精度就越低。根据设定情况以及测试条件，统计不同算法的检测精度，结果如图2所示。

由图2可知，2组传统算法在样本数量较少时检测精度低于75%，尤其是对磁场分析器运行故障检测，当样本数量达到60组时，2组算法检测精度仍低于75%，而当全部样本同时用于诊断时检测精度勉强达到85%，而研究提出方法基本不受到样本数量的影响，检测精度可达到97%以上，具有应用价值。   5 结语

以半监督学习和稀疏表示方法设计了一个新的检测算法，并在实验论证中对质谱仪的运行灵敏度进行故障检测，得到了较好的测试结果，具有一定的应用价值。但由于此次时间有限，在研究过程中仍存在少许不足之处，如实验中没有针对不同类型的质谱仪进行分析，后续研究中会针对具体的质谱仪进行检测算法设计，为实现更高精度的故障检测提供理论支持。

【参考文献】

［1］  刘转利.基于化学分析仪器计量检测问题研究[J].粘接，2020，43（8）：37-40.

[2] 叶烜荣，潘一叶，程友民，等.10kV线路缺相对系统及配变影响分析[J].粘接，2020，41（1）：167-171.

[3] 谷淑波，徐毅，金敏.Isoprime 100稳定性同位素比质谱仪故障分析及排除[J].分析测试技术与仪器，2022，28（4）：473-479.

[4] 陈金发.NexION 350X电感耦合等离子体质谱仪的使用及故障处理[J].冶金分析，2021，41（1）：92-97.

[5] 刘军坡，吴兆麟，曹玉墀，等.基于卷积神经网络的智能船舶组合导航系统故障检测算法[J].舰船科学技术，2023，45（2）：155-158.

[5]  李玺兰，段继忠.基于稀疏变换学习的改进灵敏度编码重建算法[J].北京邮电大学学报，2022，45（5）：97-102.

[6]  余琼，连危洁，温毅博，等.辉光放电质谱法测定超高纯铜溅射靶材中痕量杂质元素及其相对灵敏度因子的求取[J].理化检验-化学分册，2022，58（9）：1049-1055.

[7] 崔莹莹，陈卓，王红霞.基于半监督学习模型的协同过滤推荐算法[J].东北师大学报（自然科学版），2022，54（3）：60-66.

[9]  金向东，桑庆兵.基于半监督学习的无参考图像质量评价算法[J].激光与光电子学进展，2023，60（4）：272-279.

[10]  魏翔，王靖杰，张顺利，等.ReLSL：基于可靠标签选择与学习的半监督学习算法[J].计算机学报，2022，45（6）：1147-1160.

[11] 吴涛.基于特征提取和半监督学习的图像分类算法[J].粘接，2021，48（11）：92-97.

[12] 张万旋，张箭，薛薇，等.基于AR/CGARCH模型的液体火箭发动机自适应阈值故障检测算法[J].推进技术，2023，44（3）：223-228.

[8] 周国华，蒋晖，顾晓清，等.基于半监督子空间迁移的稀疏表示遥感图像场景分类方法[J].浙江大学学报（理学版），2021，48（6）：684-693.

[9] 南东亮，王维庆，赵启，等.基于多维Hausdorff距离算法的站域电流回路故障检测[J].电网与清洁能源，2021，37（11）：63-71.

[10] 孙玉伟，罗林根，陈敬德，等.基于声音特征与改进稀疏表示分类的断路器机械故障诊断方法[J].电网技术，2022，46（3）：1214-1222.

[11] 张明华，罗红玲，宋巍，等.基于稀疏表示和学习图正则的高光谱图像特征提取[J].光子学报，2021，50（4）：249-261.

[12] 张师鹏，李永忠，杜祥通.基于半监督学习和三支决策的入侵检测模型[J].计算机应用，2021，41（9）：2602-2608.

[13] 朱广贺，朱智强，袁逸萍.基于振动传感器的风力发电机故障检测算法[J].传感技术学报，2023，36（1）：108-112.