基于极限学习机的智能电网运行入侵检测研究

2023-09-05梁林森

粘接 2023年8期

梁林森

摘要：为解决智能电网运行入侵检测效率慢及入侵检测精度较低等问题，提出基于量子甲虫群算法优化的极限学习机模型。通过构建量子甲虫群优化算法，并引入量子力学，结合甲虫触角搜索和粒子群优化的优点，以进一步提高极限学习机算法入侵收敛性能，降低极限学习机的计算复杂度和训练时间。结果表明：随着迭代次数的增加，入侵检测测试误差逐渐减小，最小误差率为1.1%。所提出的极限学习机算法的准确率、平均 F 值和攻击准确率分别为95.82%、95.90%和95.16%。与随机森林算法相比，极限学习机可以有效提高智能电网运行入侵检测的准确性、检测率、攻击准确率，降低误报率，算法可满足实际智能电网运行入侵检测。

关键词：极限学习机；智能电网；入侵；检测研究

中图分类号： TP368.39

文献标志码： A 文章编号： 1001-5922（2023）08-0185-04

Research on intrusion detection of smart grid operation based

on extreme learning machine

LIANG Linsen

（Information Centre，Guangzhou Power Supply Bureau，Guangdong Power Grid Co.，Ltd.，Guangzhou 510000，China ）

Abstract： To further solve the problems of slow intrusion detection efficiency and low intrusion detection accuracy in smart grid operation， an extreme learning machine model based on quantum beetle swarm optimization algorithm is proposed.By constructing a quantum beetle swarm optimization algorithm and introducing quantum mechanics，combining the advantages of beetle antenna search and particle swarm optimization，the intrusion convergence performance of extreme learning machine algorithm is further improved，and the computational complexity and training time of extreme learning machine are reduced.The experimental results show that as the number of iterations increases，the error of intrusion detection testing gradually decreases，with a minimum error rate of 1.1%.The accuracy，average F value and attack accuracy of the proposed extreme learning machine algorithm are 95.82%，95.90% and 95.16% respectively.Compared with random forest algorithm，extreme learning machine can effectively improve the accuracy，detection rate and attack accuracy of intrusion detection in smart grid operation，and reduce false alarm rate，and extreme learning machine algorithm can meet the actual intrusion detection in smart grid operation.

Key words： extreme learning machine;smart grid;invasion;detection research

如果智能電网受到攻击，人们的生活将受到严重影响[1]。智能电网给社会带来了便利，也带来了新的挑战[2]。基于此，我国相继在智能电网安全方面开展了一些研究，探索了智能电网入侵检测领域。

基于异常的入侵检测系统用于检测系统的异常行为，当检测行为与正常行为有很大偏差时会发出警告消息[3]。目前基于异常的入侵检测研究主要集中在基于统计的入侵检测、基于传统机器学习的入侵检测、基于可视化的入侵检测系统、基于神经网络的入侵检测等方面[4-6]。其中，极限学习机作为一类具有自适应特性的大型非线性动力系统，在入侵检测识别中具有很好的应用前景。因此可以利用极限学习机算法的自学习能力，来解决网络入侵检测中的某些问题。极限学习机具有多数据并行计算、自适应学习能力好、可搜索速度快、抗干扰性能强、处理失真、不完整数据信息的能力等优点[7]，非常适合从大型网络中复杂、大量数据中识别入侵数据。然而，传统的极限学习机算法收敛速度慢，容易陷入局部极小值的限制，限制了极限学习机的应用[8]。

对此，部分研究人员提出了相应的改进策略。基于PCA-BP神经网络，采用主成分分析方法对BP神经网络进行了参数选取和权值选取[9

]。将人工蜂群和BP神经网络相结合，优化了网络模型的收敛速度和准确性[10]。提出了基于粗糙集理论的域概念，并利用域粗糙集理论来简化实验数据和BP网络结构[11]。此外，量子计算越来越受到关注，量子计算与人工智能算法的结合也广泛应用于各个领域。例如，提出将量子粒子群优化算法应用于城市电动汽车充电站的规划，并证明了其有效性和可行性[12]。引入一种基于量子粒子群优化算法的混沌搜索来提高初始种群的质量，并将其应用于水电站的优化调度，有效地提高了梯级水能的利用率[13]。提出了一种基于量子遗传算法的网络优化覆盖算法，以便在给定传感器节点数时获得最大的网络覆盖率[14]。

研究提出了一种基于量子甲虫群优化的极限学习机入侵检测模型。与其他模型相比，该模型具有更快的收敛速度和更高的精度[15]。将量子力学的基本原则引入到量子甲虫群方法中，并将其与微粒群方法进行了融合。使算法更容易跳出局部最优解。将此模型应用于改进的极限学习机可以提高检测入侵网络的效率。

1 智能电网运行入侵检测算法建立

甲虫群算法可以模拟甲虫的飞行过程[16]。甲虫群算法采用迭代法逐步逼近最优解。由于甲虫群算法中只有个体，与其他智能算法相比，具有算法简单、计算速度快的优点。且甲虫群算法侧重于过程搜索，这有利于解决单峰问题。但是，也有可能出现搜索精度低的问题。而粒子群优化（PSO）是一种群体进化优化算法，有利于多峰问题的优化[17]。但是，也存在过早收敛、收敛精度低、收敛困难等缺陷。因此，本文提出了一种与量子计算相结合的量子甲虫群模型。根据甲虫群算法和粒子群优化算法各自的优势，单个甲虫可以从自己的经验以及群体经验中学习[18]。因此，单个甲虫可以有目的、有启发性的移动，从而提高算法的收敛性能。最后，在迭代后期引入精英策略来增加种群的多样性，以避免算法陷入局部最优。

1.1 甲虫群算法

甲虫群算法的基本原理如下。甲虫在进食时不知道食物的具体位置，所以它用2根天线来探测食物的气味并确定其方向。如果甲虫的左边天线收到的气味比右边天线强，甲虫就会向左边飞去，否则就向右边移动。基于这个简单的原则，它可以很容易地找到食物[19]。详细步骤如下。

假设甲虫的头在任何方向上都是随机移动的，那么从右边的天线到左边的天线的矢量方向也一定是随机的。因此，对于 n 维空间的优化问题，可以生成一个随机矢量来表示和规范。

b ′= rands（n， 1 ） ‖rands（n，1）‖

（1）

其中 n是空间维度，rands（n，1）为一个随机函数。

左边和右边的天线之间的关系可以表示为：

x 1－x r=d o·d ir （2）

其中 x l 和x r 可以用中心点来表示：

x 1=x+（d 0·d ir ）/2x r =x－（d 0·d ir ）/2

（3）

其中 x l是搜索区域的左侧，x r 是右侧。

进一步确定左侧和右侧天线的气味强度，其中 f（x 1）和 f（x r ）代替左右位置， f（x）为适配函数。

为了制定搜索行为步骤，进一步生成了以下迭代模型。迭代更新甲虫的位置以探测气味。

ΔF=f（x r ）－f（x 1）

（4）

xT+1=x t －δtb sign （ΔF）（5）

其中 x是甲虫第t次迭代中的中心点坐标。第t 次迭代的步長为δt，sign（ x ）为符号函数。

1.2 粒子群优化算法

粒子群优化算法的灵感来自于生物种群的行为特征，并被有效地用于解决复杂的优化问题。在粒子群优化系统中，通过连续迭代寻求最优解或近似最优解，通常用于解决各种优化问题。在粒子群优化模型中，每一个粒子都是最优解，而每一个粒子的运动强度都是以目标函数为基础。首先对每一个微粒进行初始化，微粒都具有对应的初始点。其次，该粒子会按照目前最好的粒子进行更新。所有的微粒都是在其各自找到的最优位置（pbest）以及在全部微粒群体中找到的最优位置（gbest）来实现对自身状态的调节。一维向量可用于表示所有粒子的位置和速度，即：

x i=［x i1，x i2…x id］，v i=［v i1，v i2…，v id］（6）

在每次迭代中，粒子速度和位置更新公式：

vt+1 id=wvi id+c 1r 1（ pbest t id－xt id）+c 2r 2（gbestt d－xt id）（7）

xt+1 id=xt id+v t+1 （8）

w=w max －（w max －w min ）× t t max （9）

式中： t是当前的迭代次数；c 1、c 2为学习因子（一般值取为2）；r 1，r 2是介于（0，1）之间的独立随机数。w max和 w min是惯性权重；最大值和最小值通常分别为0.9和0.4； t max是最大迭代次数。

1.3 量子甲虫群算法优化极限学习机

甲虫群算法中的聚类可以用力学中的粒子束缚态来描述[20]。在量子力学中，量子粒子反映与束缚态相同的行为，处于量子束缚状态的粒子可以以一定的概率密度出现在空间中的任何一点。当粒子靠近中心 “p”时，发生的概率更大，当与p的距离接近无穷大时，概率密度接近零。其他势能模型具有过于复杂而无法模拟的波函数，有些容易过早成熟，因此选择势阱模型δ。

在量子空间中无固定轨道的质点，它的速度与位置都无法同时被确定。所以粒子的状态由波函数 φ（X，t）描述，其中[WTHX]X[WTBZ]= x，y，z 是粒子在三维空间的位置矢量。波函数的物理含义是：波函数模数的平方是粒子在空间某一点上出现的概率密度，即：

φ 2d x d y d z=Q d x d y d z

（10）

其中 Q 是概率密度函数，满足归一化条件。

∫ +SymboleB@

－SymboleB@

Q d x d y d z=1

（11）

其中量子空间中粒子运动的动力学方程为薛定谔方程。

ih - t φ（X，t）=H ^ φ（X，t）

（12）

其中 H ^ 为哈密顿量， h 为普朗克常数。哈密顿量具有以下形式。

H ^ =－ h 2 2 m SymbolQC@

2+V（X）

（13）

其中 m是粒子的质量，V（x）为粒子所在的势场。

假设甲虫群系统是一个量子粒子系统，每个粒子都有量子行为，其状态由波函数描述。存在以某种形式的以π点为中心的吸引势。设π表示为p，粒子的位置为X。在点p建立一维势阱δ，其势能函数表示为：

V（ x ）=－γδ（X－p）=－γδ（Y）（14）

其中 Y=X－p ， m 为粒子的质量。

1.4 模型构建

首先构建极限学习机模型。传统的极限学习机算法使用显式非线性特征映射。对于更复杂的分类、回归和其他非线性模式识别任务，通常需要隐藏层神经元，从而产生非常复杂的网络结构。因此本文采用3层结构，即输入层、隐藏层和输出层。输入层面的每一个神经元与隐藏层面的全部神经元相连。隐藏层里的每一个神经元与输出层里的全部神经元相连。

当使用甲虫群算法优化极限学习机的输入层权重时，每个粒子的位置向量 X 表示一组极限学习机的权重。采用甲虫群算法搜索最优权重，通过迭代使粒子在终止条件下的适应度值最小化，找到粒子的最佳位置。该位置向量用作极限学习机的最终输入权重和阈值，用于极限学习机测试验证。本文将训练样本极限学习机输出的均方误差作为适应度值。

2 结果与讨论

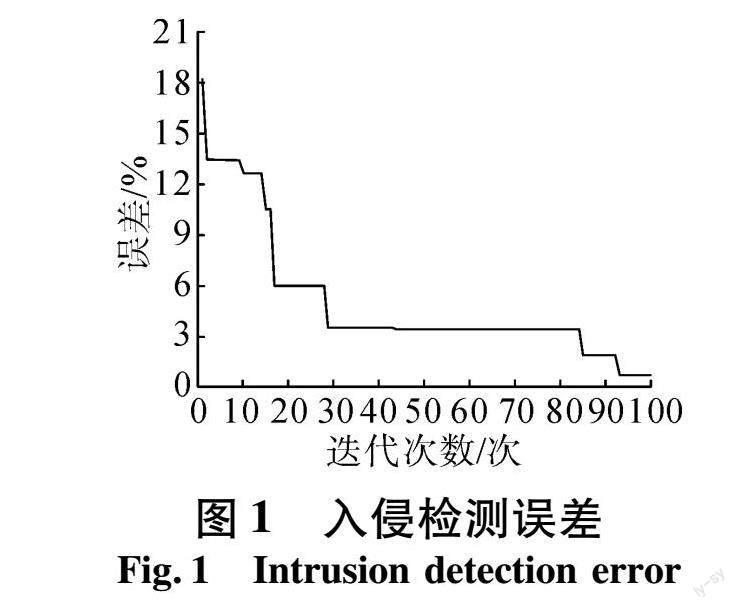
2.1 入侵检测误差

本文将极限学习机模型用于智能电网运行入侵检测实验研究。实验在Windows10系统和python平台上进行仿真。使用智能电网中的KDDCUP99和CICIDS2017数据进行实验。在实验中，量子甲虫的种群为40，模型训练迭代次数为100，惩罚系数c为80 000。

在极限学习机入侵检测算法步骤的基础上，通过参考经验和测试多个参数，选取一组相对最优的参数进行设置，并将种群规模设置为20。最大遗传代数为100，变异概率为0.01，交叉概率为0.7。隐层神经元的激励函数采用Sigmoid函数。基于极限学习机的入侵检测的误差如图1所示。极限学习机算法共进行了100次迭代。在第0次迭代时，为原始极限学习机，误差率为18.2%。随着迭代次数的增加，测试误差逐渐减小，最小误差率为1.1%，说明量子甲虫群优化极限学习机算法是有效的，且原始极限学习机的输入权重和隐藏层神经元的偏移量得到有效优化。同时可观察到迭代次数30～82次时，误差保持在3.4%，进一步表明量子甲虫群算法有效地优化极限学习机的输入权重和隐藏层神经元的偏移量。通过提高模型的性能，可以极大保持极限学习机的训练速度，同时更好地提高智能电网入侵检测的准确性。

2.2 极限学习机入侵检测性能

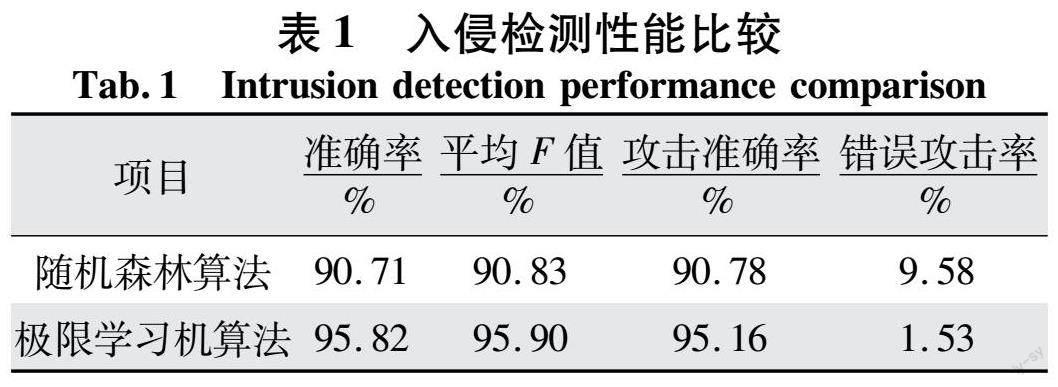
利用提出的甲虫群算法优化极限学习机和随机森林算法用训练数据集和测试数据集进行测试，以进一步突出基于极限学习机的智能电网运行入侵检测性能。表1为极限学习机算法和随机森林算法性能的比较。

如表1所示，甲虫群算法优化极限学习机的入侵检测性能优于随机森林算法。此外，所提出的极限学习机算法的准确率、平均F值和攻击准确率等评价指标分别为95.82%、95.90%和95.16%，高于随机森林算法；且极限学习机算法的错误攻击率为1.53%，远低于随机森林算法错误攻击率（9.58%）。因此，提出的极限学习机可以满足实际智能电网系统入侵检测的能力。

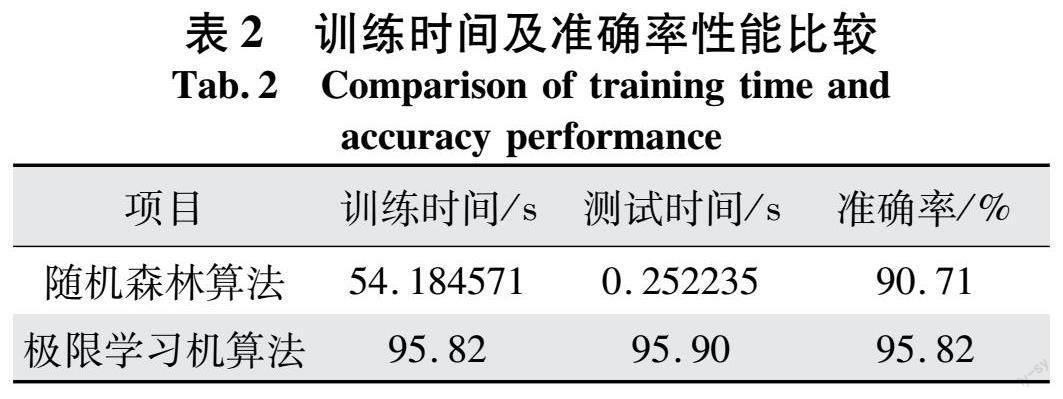
此外，為了证明甲虫群算法优化极限学习机在计算效率方面的优势，与随机森林算法在相同训练数据集进行准确性、训练和测试时间结果对比，实验结果如表2。

如表2所示，极限学习机算法的准确率为95.82%，与随机森林算法的90.71%相比提高了5.11%。此外，极限学习机算法的训练和测试时间分别为54.184 571 s和0.252 235 s，而随机森林算法的训练和测试时间分别为21.283 896 s和0.128 424 s。且可以观察到与随机森林算法相比，极限学习机算法节省了60.72%的训练时间和49.09%的测试时间。综上所述，基于所提出的甲虫群算法优化极限学习机可以提高智能电网入侵检测测试时间，且其入侵检测准确性及攻击准确率较高，可以有效提高智能电网入侵检测。

3 结语

通过建立基于量子甲虫群优化的改进极限学习机网络入侵检测算法，有效解决了现有智能电网入侵检测准确低等问题。将极限学习机算法应用于入侵检测领域。实验结果表明，与随机森林算法相比，极限学习机算法在各项评价指标上具有明显的优势。极限学习机算法的错误攻击率为1.53%。且极限学习机算法的训练和测试时间为54.184 571 s和0.252 235 s，极大降低智能电网入侵检测所需时间。

【参考文献】

［1］席磊，何苗，周博奇，等.基于改进多隐层极限学习机的电网虚假数据注入攻击检测[J].自动化学报，2023，49（4）：881-890.

[2] 王萍利.基于人工智能技术的化工企业计算机网络安全防御系统设计[J].粘接，2021，47（8）：106-109.

[3] 张晓琴，汪云飞，胡春强.基于改进极限学习机的数据采集与监控系统攻击检测模型[J].南京航空航天大学学报，2021，53（5）：708-717.

[4] 刘菲菲，伍忠东，丁龙斌，等.基于改进在线序列极限学习机的AMI入侵检测算法[J].计算机工程，2020，46（9）：136-142.

[5] 郭华，李颖，江浩，等.基于物联网技术的电力线路信息网入侵检测系统设计[J].电子设计工程，2020，28（18）：131-135.

[6] 周念成，廖建权，王强钢，等.深度学习在智能电网中的应用现状分析与展望[J].电力系统自动化，2019，43（4）：180-191.

[7] 段立峰.基于最大熵原理的电子商务混合入侵行为信息智能化检索方法研究[J].粘接，2020，44（10）：141-144.

[8] 陈丽惠，李哲，周键宇，等.基于ELM和迁移学习的电网设备多因素综合故障率分析方法[J].计算机测量与控制，2023，31（4）：30-35.

[9] 吴谦，陈嘉，周瑾瑜，等.基于快速区域卷积神经网络的电网通信網入侵威胁预先识别方法[J].电气自动化，2022，44（6）：98-101.

[10] 庞红旗，高飞翎，程国开，等.基于经验模态分解和极限学习机的日输电量分时建模预测[J].智慧电力，2021，49（9）：63-69.

[11] 郭静.基于计算机的网络安全漏洞及其有效防范措施[J].粘接，2019，40（10）：187-189.