基于无人机的炮位侦校雷达目标模拟技术

王昕宇

(南京海清科技有限公司,江苏 南京 210036)

0 引 言

炮位侦校雷达是现代陆军重要的战场情报侦察设备,在确定敌方炮位阵地及校正我方炮弹落点精度等方面发挥着重要的作用。随着雷达技术的广泛使用[1],炮位侦校雷达在研制、生产、维护和日常训练中,均需采用雷达目标模拟器进行性能测试、故障诊断和操作员训练,传统的做法是在外场架设目标模拟阵列[2],通过控制目标回波信号的延时和多普勒[3]以及阵列天线的辐射顺序,来模拟目标的运动轨迹。受空间位置的限制,该模拟器只能模拟单目标的飞行轨迹,难以实现同时多批次目标的模拟能力。随着无人机技术的发展,以及无人机高精度和快响应控制能力的大幅提升,将无人机应用到雷达目标模拟上来已成为可能,由无人机搭载小型雷达目标模拟器,通过控制无人机在空中按照一定航迹运动,模拟弹丸方位角和俯仰角的变化,结合模拟器对接收雷达信号的调制转发,可以实现高逼真的弹道轨迹模拟[4]。

1 工作原理

无人机载目标模拟器电路组成框图如图1所示。模拟器工作时,接收天线接收雷达发射信号,经过变频模块下变频为中频信号,目标板根据设定的工作参数对输入中频信号经过采样和存储,经距离延时和多普勒调制后,由D/A恢复为模拟中频信号,经上变频和幅度调制后注入或空馈给雷达接收机。无人机载雷达目标模拟器电路组成框图如图1所示。

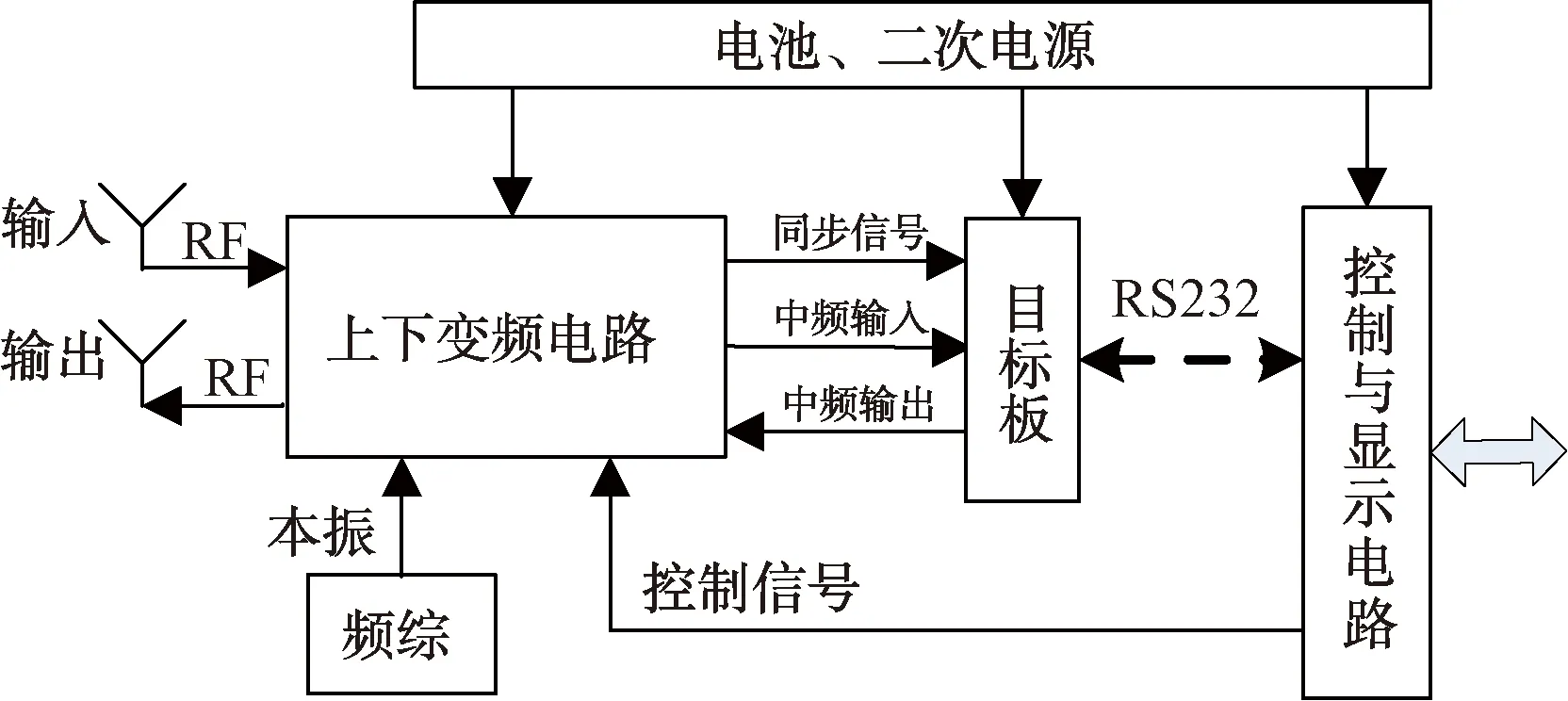
图1 无人机载雷达目标模拟器电路框图

本文重点研究基于无人机的炮弹目标逼真模拟技术,弹丸的距离、速度和雷达截面积(RCS)由目标模拟电路完成,而空间位置变化需要精确控制无人机来实现。无人机载目标模拟器可以模拟各种炮弹的运动轨迹。以典型的榴弹炮为例,假设炮弹初速度为1 000 m/s,最大射程为50 km,弹道仰角范围为6°,雷达波束宽度为2.5°,测角精度为0.25°,精确模拟一次弹道轨迹需要控制无人机位置变化大于48次。如果一次弹道飞行时间50 s,那么就要求无人机一次位置变化的控制时间小于1 s,这样就对无人机控制系统提出了挑战。

2 无人机控制电路设计

2.1 经典PID控制技术

典型的无人机飞行控制框图如图2所示,主要包括位置控制器和姿态控制器,姿态控制保证无人机空中飞行的稳定性,位置控制保证无人机自主跟随的精度。整个控制器的输入是期望的位置Pd(xd,yd,zd)和偏航角θd,输出是期望总拉力fd和三轴力矩τd。位置控制器通过比较无人机实际位置p(x,y,z)与期望位置Pd(xd,yd,zd)的差值,根据控制算法计算出四旋翼无人机的期望总拉力fd和期望俯仰角βd以及滚转角γd,姿态控制器通过比较实际姿态角(α,β,γ)与期望姿态角(αd,βd,γd)差值计算出力矩参数τd,然后总拉力和力矩输入到控制分配器得到电机转速,使得无人机到达期望的位置[5-6]。

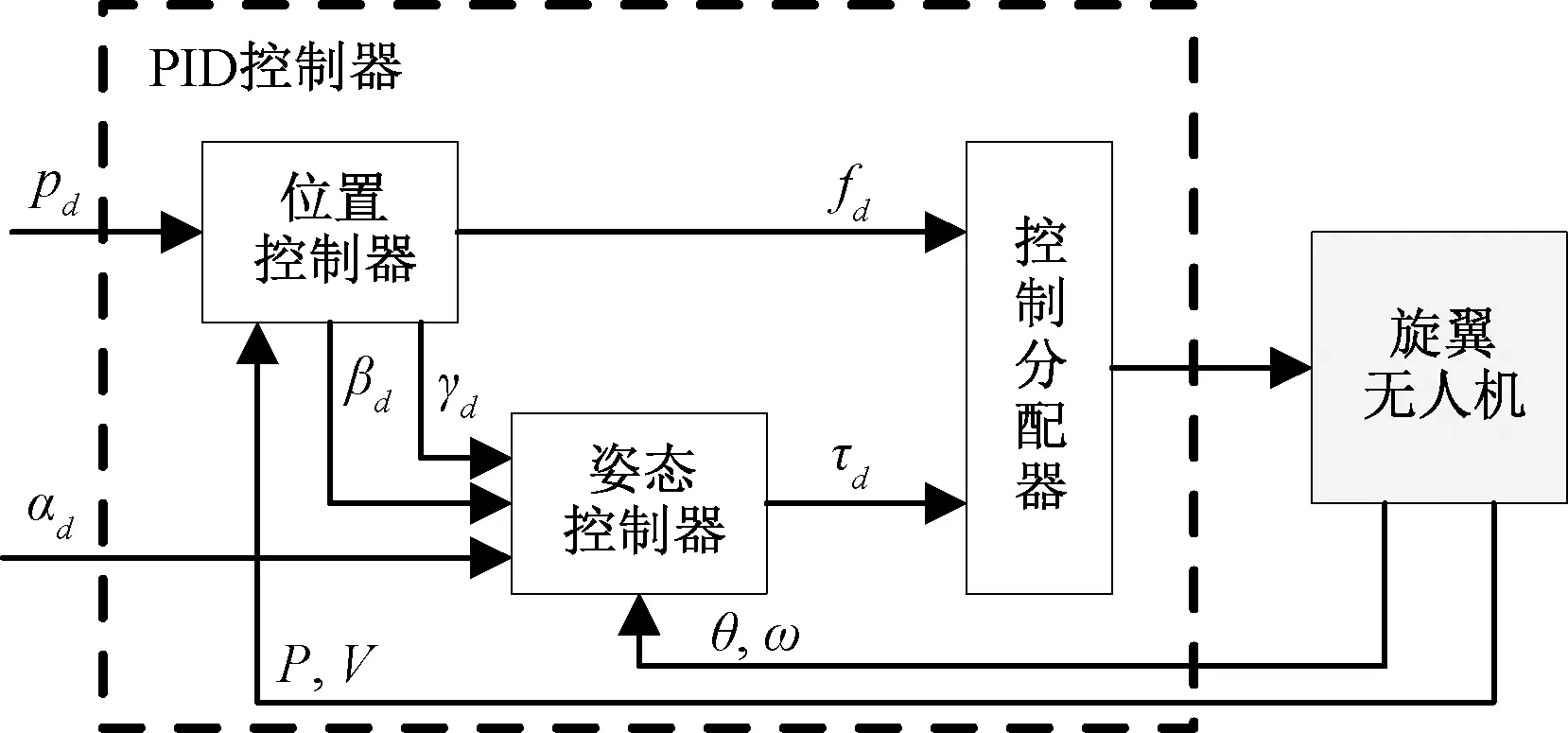
图2 四旋翼无人机飞行控制图

经典的比例、积分、微分(PID)控制器由比例环节、积分环节和微分环节组成。比例环节只考虑当前的偏差值,对系统偏差迅速做出反应;积分环节会考虑过去的偏差情况,对系统偏差进行积分,可以减少偏差的积累,提高对被控对象的控制精度;微分环节考虑近期偏差的变化情况,并预估控制对象将来的变化趋势,以改善被控对象的动态性能指标[7-8]。

假设PID控制器的输入期望值为r(t),实际输出值为y(t),二者的差值e(t)为:

e(t)=r(t)-y(t)

(1)

PID控制规律的表达式如下:

Kd(e(n)-e(n-1))

(2)

式中:Kp、Ki、Kd分别为比例系数、积分系数和微分系数。

2.1.1 姿态控制器

姿态控制器采用串级PID控制策略[9],分为内外两环控制,内环为角速度控制环,外环为角度控制环。角速度控制环的引入,可以提高无人机系统的鲁棒性,改善系统的动态性能,同时对外环输出的干扰起到有效的抑制作用。姿态控制器电路组成框图如图3所示。

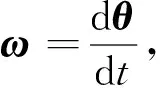
(3)

式中:K1、K2、K3分别为横滚、俯仰及偏航的环路控制系数,均大于0。

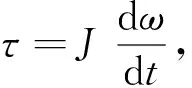
Kωd(eω(n)-eω(n-1))

(4)

式中:eω=ω-ωd;Kωp,Kωi,Kωd∈R。

实际姿态角与期望姿态角的差值经外环作用输出期望的角速度,实际角速度和期望角速度的差值再经内环得到输出力矩,传递给四旋翼无人机系统模型。

2.1.2 位置控制器

位置控制器电路框图如图4所示,同样采用串级PID控制方法,内环为速度控制环,外环为位置控制环。位置控制器分为水平控制通道和高度控制通道,水平控制通道先求出实际水平位置与期望水平位置的差值,经外环输出期望的水平方向速度Vhd,实际速度与期望速度的差值eVh再经内环得到期望的滚转角βd和俯仰角γd,传递给姿态控制器。高度控制通道根据实际高度与期望高度的差值,通过外环输出期望的高度方向速度Vzd,实际速度与期望速度的差值经内环得到期望的总拉力fd,传递给四旋翼无人机。

图4 位置控制器电路框图

控制器外环输出的水平方向速度期望值Vhd和高度方向速度期望值Vzd如下:

Vhd=Kph(Phd-Ph)

(5)

Vzd=Kpz(Pzd-Pz)

(6)

水平方向实际速度与期望速度的差值eVh,以及高度方向实际速度与期望速度的差值eVz如下:

eVh=Vh-Vhd

(7)

eVz=Vz-Vzd

(8)

控制器内环输出的水平方向期望姿态角度Θhd如下,包括滚转角和俯仰角:

KVhd(eVh(n)-eVh(n-1))

(9)

期望的总拉力fd为:

KVhd(eVz(n)-eVz(n-1))

(10)

2.2 变论域模糊PID控制技术

变论域模糊PID控制技术对于时变和非线性系统具有很好的控制效果,能够缩短稳定时间,提高抗干扰能力[10-12]。本文拟采用二维模糊控制器,控制器的输入为误差e和误差变化率ec,输出为PID控制器3个参数Kp、Ki、Kd的修正量。模糊PID控制器不断获取e和ec的数值,经过量化因子变换和模糊化接口处理,将输入量转换为模糊处理能够识别的变量,模糊化推理机由专家经验规则和智能算法组成,经模糊推理得到控制系统的调整参数,通过解模糊算法得到Kp、Ki、Kd的调整量,再与Kp、Ki、Kd的初始值相加得到最后的控制参数。变论域模糊PID控制电路框图如图5所示。该控制系统不仅动态响应特性得到改善,而且抗外界干扰能力也得到提高。

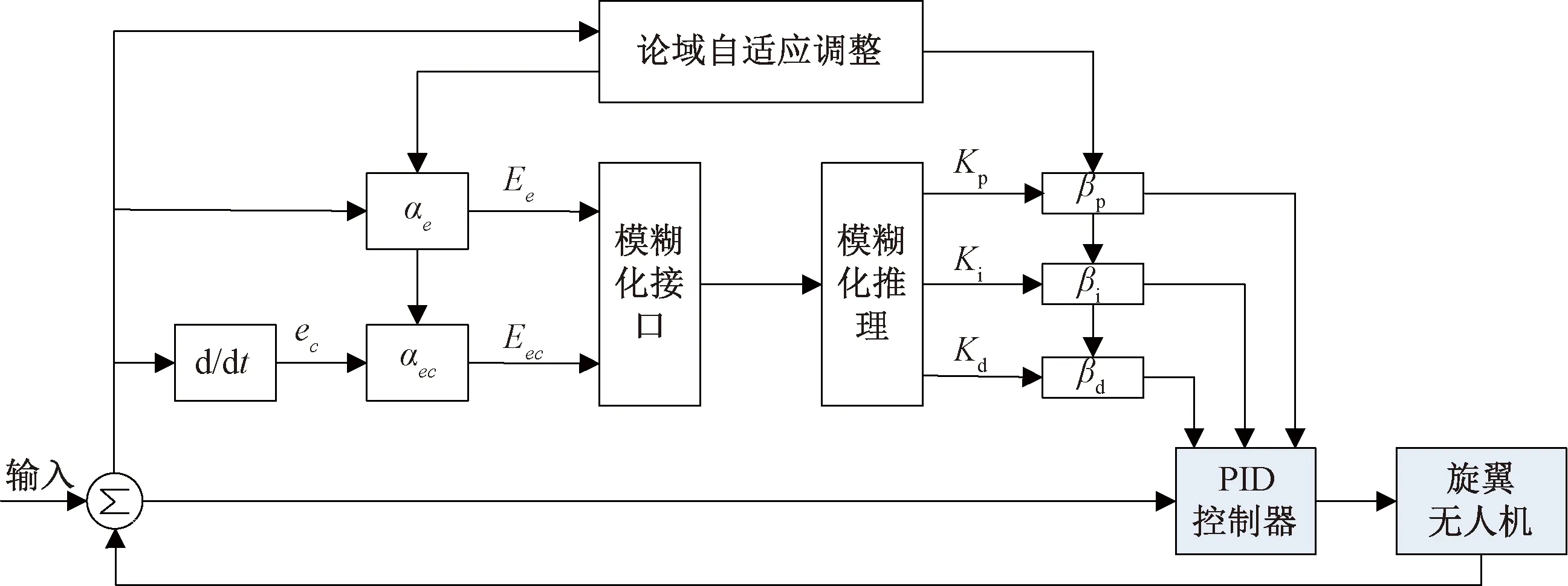
图5 变论域模糊PID控制电路框图

本文使用7个模糊变量,分别为负大(NB)、负中(NM)、负小(NS)、零(ZO)、正小(PS)、正中(PM)、正大(PB),模糊子集为{NB,NM,NS,ZO,PS,PM,PB},采用三角型隶属函数来确定模糊子集,模糊PID控制器3个参数的调整原则如下:

(1) 当|e|较大时,为了系统可以达到快速跟踪的效果,所以选择较大的Kp;同时为了避免偏差变化率过大,需要抑制微分作用,防止其快速增加,选择较小的Kd;为了防止产生积分饱和,出现过量的超调,一般取Ki为零。

(2) 当|e|和|ec|为中等大小时,为了避免超调较大,所以选择较小的Kp,也可以选择较小的Ki;同时为了保证系统的快速响应,选择适当的Kd。

(3) 当|e|较小时,为了系统可以达到良好的稳定控制效果,选择较大的Kp和Ki;同时为了避免系统振荡,提高抗干扰能力,在|ec|较小时可以选择较大的Kd,|ec|较大时选择较小的Kd。

对于模糊控制规则,需要相应的语句进行描述[13]。由e、ec、ΔKp、ΔKi、ΔKd构成的49条模糊规则用if-then语言格式进行表示,每一条语句都代表一个模糊关系。经模糊推理后得到的是模糊量,但输出给控制对象的值必须是一个精确量,所以还需对结果进行解模糊。本文采用加权平均法作为解模糊方法。得到精确值后,还需与比例因子相乘得到实际的控制系统输出值。

3 仿真分析

本文以四旋翼无人机为例,在MATLAB/Simulink中搭建飞行控制系统的仿真模型,将系统各部分进行模块化处理,分别搭建串级PID控制模型、模糊PID控制模型和变论域模糊PID控制模型,进行仿真和分析。四旋翼无人机仿真参数如表1所示。

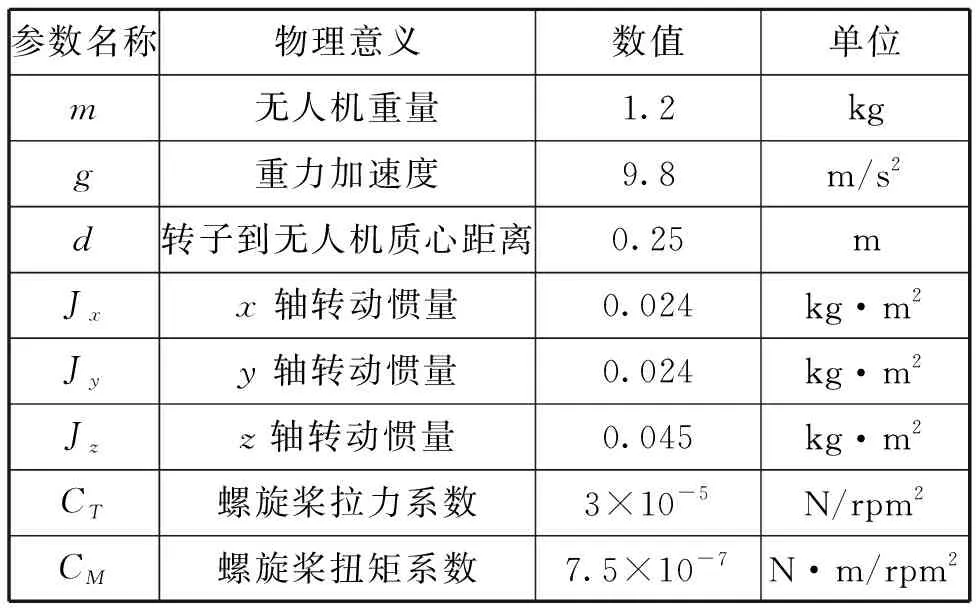
表1 四旋翼无人机模型参数

设系统初始位置为 (0,0,0),初始姿态角为 (0,0,0),仿真时终点位置为 (1,1,2),位置响应曲线如图6～图8所示。3种控制算法对应的上升时间、超调量、峰值时间和稳态时间如表2所示。

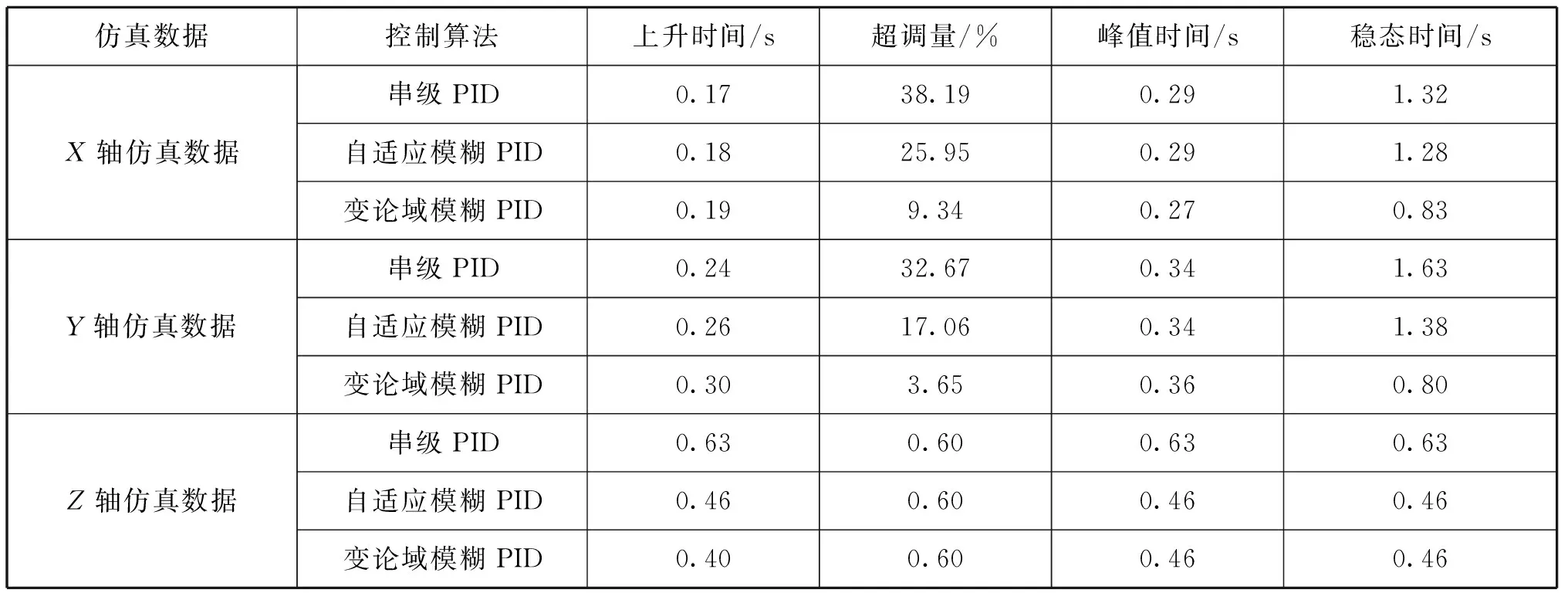
表2 四旋翼无人机仿真数据

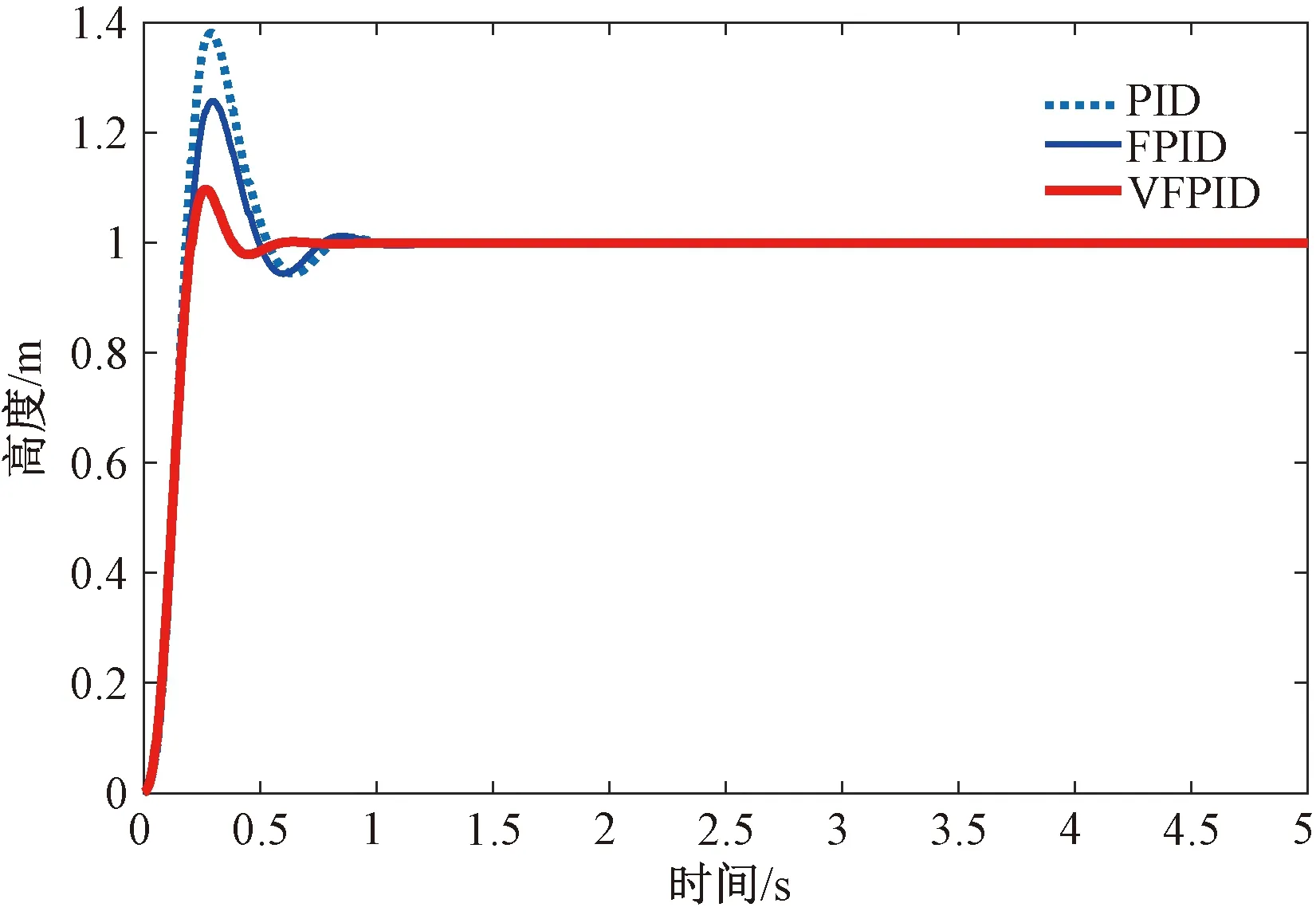
图6 无人机X轴分量仿真结果

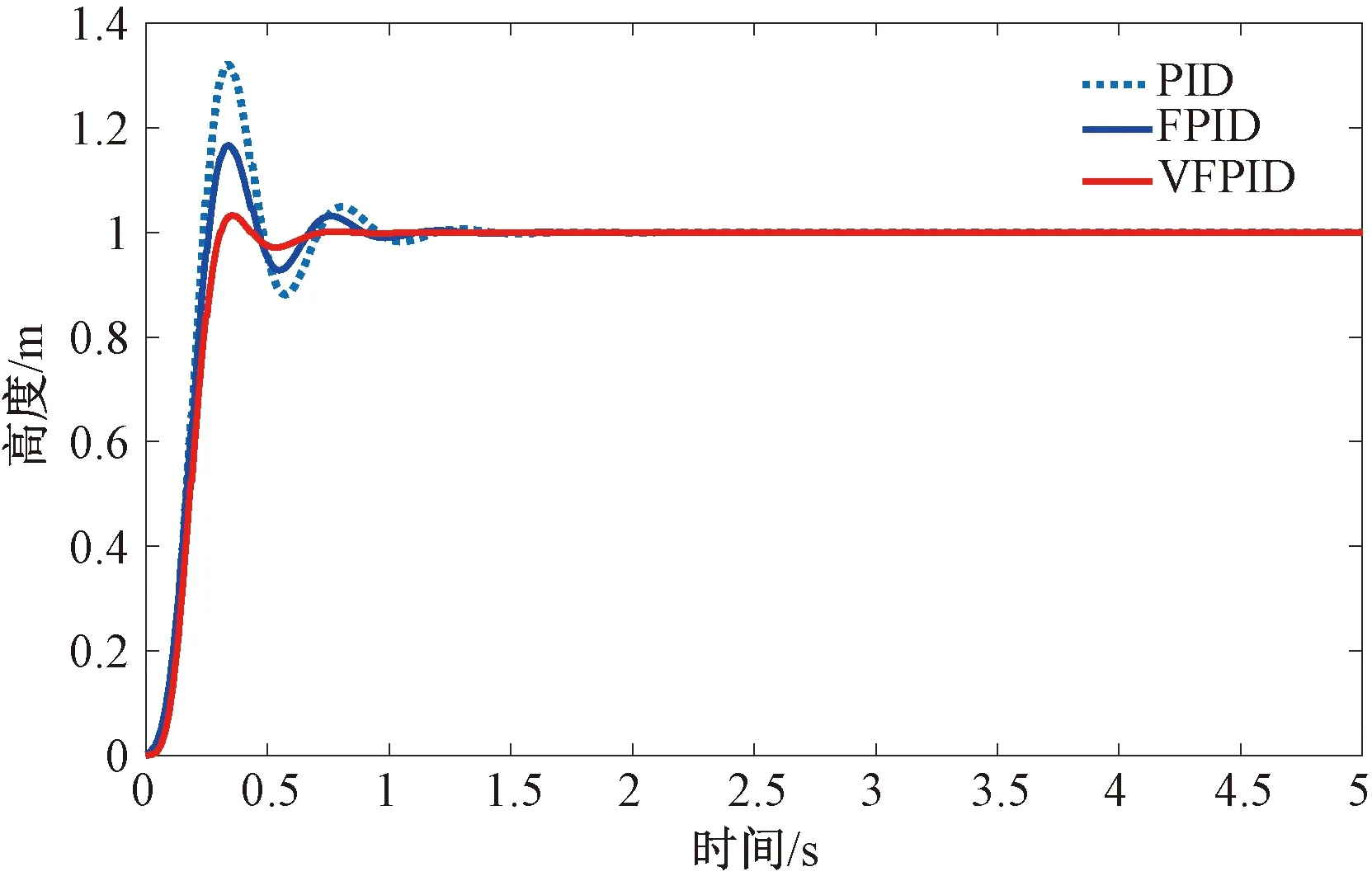
图7 无人机Y轴分量仿真结果

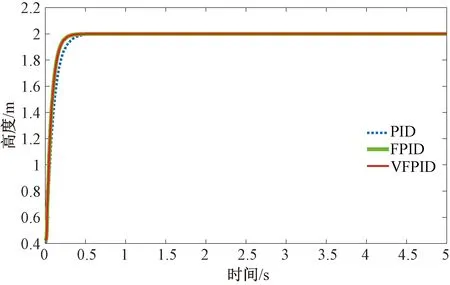
图8 无人机Z轴分量仿真结果

通过比较表2的仿真数据可以看出,变论域自适应模糊PID控制算法具有上升时间短、超调量小、稳态时间短等优点,而且该控制算法具有很好的稳定性和鲁棒性。如果在炮弹目标模拟器中采用该控制算法,无人机位置控制精度和控制速率均能满足要求。

4 结束语

针对阵列式炮位侦校雷达目标模拟器存在的问题,本文研究了基于无人机的雷达目标模拟器。小型雷达目标模拟电路可以安装在无人机上,接收的雷达辐射信号经过延时、多普勒和幅度调制,可模拟目标的距离和速度信息,目标的角度变化是通过获取目标的期望位置、控制无人机姿态使其朝着期望位置运动。为了精确模拟弹丸目标的运动轨迹,满足雷达测量需求,无人机控制系统的选择和控制参数的设计是模拟器的关键,要求无人机控制环路响应速度快、振荡幅度小、抗干扰能力强。本文研究了无人机控制系统的原理和算法,提出了基于变论域模糊PID控制技术,并与常规串级PID控制算法和模糊PID控制算法进行了对比,变论域模糊PID算法收敛速度更快,稳定性更好,超调量更小,能够大幅提高无人机的位置跟踪效果。同时,本文针对四旋翼无人机进行了建模仿真,仿真结果表明变论域模糊PID的控制算法不仅控制速度快,而且具有很好的鲁棒性和抗扰性。