3D打印零件的尺寸精度及控制

2023-09-05高海亮周宇强程建明宋桂珍

中国塑料 2023年8期

高海亮，胡程，周宇强，刘欣，程建明，宋桂珍

（太原理工大学机械与运载工程学院，太原 030000）

0 前言

熔融沉积建模是目前使用最广泛的3D 打印成型工艺，其关键优势是能够生产形状和几何模型非常复杂的一体化零件，并在航空航天、生物医学等方面广泛应用［1‑3］。

FDM 是将热塑性聚合物丝材在喷嘴内加热融化，喷头沿零件截面轮廓和填充轨迹运动，同时挤压沉积到运动的工作台上，利用高温自黏结性逐层堆积成型［4］。丝材在熔融堆积过程中，由于体积收缩产生的内应力会引起原型底部的翘曲变形或在原型内部引起分层，严重影响了制件的尺寸精度，是当今快速成型技术领域迫切需要解决的问题之一［5］。国内外很多学者对翘曲变形进行了研究，Panda 等［6］基于线宽补偿、打印速度、填充速度和层厚4 个变量来明确量化FDM 原型的翘曲变形和尺寸误差，表明层厚和打印速度对翘曲变形有影响，填充速度和线宽补偿对尺寸误差影响较大。Syrlybayev 等［7］利用ANSYS 建立了3D 打印过程的热力学有限元模型，通过模拟和试验表明翘曲随层厚的增加而减小。王天明等［8］定量分析了堆积层数、环境温度和ABS 材料的线收缩率对原型翘曲变形的影响。张捷等［9］分析了FDM 翘曲变形过程，建立了翘曲变形的数学模型，指出提高打印环境温度、减小层厚和提高打印速度可以有效改善制件的翘曲变形。杜林芳［10］针对FDM 工艺过程中的翘曲变形缺陷，提出分层厚度、打印温度对翘曲变形有较大影响，托板温度和产品壁厚次之，通过对FDM 的成型工艺优化，使打印精度提高了44.4 %。然而，如前所述许多学者对FDM制件的翘曲变形进行了不同角度的研究，但目前研究结果不尽一致，且对于如何选择聚乳酸（PLA）材料FDM 成型参数，减小成型过程中的翘曲变形量未见有系统研究的报道。

本文以目前使用最广泛的PLA 为打印材料，通过建立翘曲变形的数学模型分析影响零件底部翘曲的影响因素，并基于L25(56)正交试验，研究了FDM 过程中分层厚度、喷嘴温度、托板温度和填充率及层数和断面长度对零件底部翘曲变形的影响，最后对结果进行了极差分析、方差分析和单因素指标分析，确定了每个指标最佳的3D 打印参数，为FDM 制件的质量工艺控制提供了理论依据和应用指导。

1 FDM理论分析模型

丝材在熔融堆积成型的过程中，会经历固体—熔融体—固体三相的变化，聚合物丝材温度会快速加热和冷却，导致内应力不均匀变化，从而引起零件翘曲变形，故打印层间的应力‑应变是导致翘曲变形的根本原因。

1.1 模型基本假设

对FDM 成型过程中内应力的产生和翘曲变形进行数学分析，需做一些合理的假设。基本假设如下：（1）半熔融态丝材从熔融温度(Tm，℃)冷却到玻璃化转变温度(Tg，℃)的过程中，热塑性丝材受到较小的外力就会发生较大的变形，抵抗外力的能力很小，因此在这一过程中并没有内应力聚集，内应力主要在玻璃化温度到成型室温度(Te)的过程中产生，如图1所示。（2）将每个成型层看作是均质层，且认为成型层内的丝材是瞬间堆积成型；假设每个堆积层面是由断面为方形的半熔融丝材按“之”字形堆积成的，各层紧密无孔隙，无相对位移。（3）高温挤出的丝材瞬时就冷却到玻璃化温度以下，且成型部分温度、托板温度与环境温度一致。

图1 丝材沉积成型原理Fig.1 Principle of silk deposition forming

1.2 翘曲变形数学模型

如假设（1），由于新沉积层不完全收缩产生的内应力发生在Tg冷却到Te的过程中，在此过程中内应力由3 部分组成：新堆积层自由收缩产生的层间应力（δ1，mm），已成型部分翘曲变形产生的弯曲应力(δ2，mm)；施加在已成型部分的应力(δ3，mm)，见式(1)～(2)：

式中α——丝材线膨胀系数，1 mm/℃

E——热变形阶段的弹性模量，MPa

∆T——热变形温差，℃

式中R——翘曲变形的翘曲半径，mm

D——弯曲变形中性层到挤出嘴的距离，mm

总内应力（δ，mm）=δ1+δ2+δ3；即得式（3）：

式中 ∆T——阶跃函数

s——已成型高度，mm

Z——变形的中性层到挤出口距离，mm

h——原型高度，mm

根据成型后的零件内应力和为零，且内应力对成型原点的合力矩也为零，积分见式（4）～（5）：

方程中包含了R、D、δ33 个未知参数，通过参数合并将未知数合并为2 个。令δ*=δ3-ED/R，则式（4）～（5）可简化为式（6）～（7）：

积分区间分为2 部分，当0 ≤Z≤s时，∆T=0；当s≤Z≤h时，∆T=Tg-Te；联立上述方程组得到式（8）：

此为新堆积层为1层时的变形率，对于熔融沉积成型，h和s之差就是堆积层厚∆h。当层数为n的堆积层有s/h=（n-1）/n，令∆h=h-s，则上式可简化为式（9）：

又有翘曲变形率（K）=1/R，故K=6α∆T(n-1)/n3∆h。

此外，翘曲半径、最大翘曲变形量与原型的断面长度相关，如图2 所示。根据图2 可知零件的最大翘曲变形量（δ，mm）与零件的翘曲半径（R，mm）和线性长度（L，mm）几何关系为Rsinθ=L/2，cosθ=R-δ/R，化简得到式（10）：

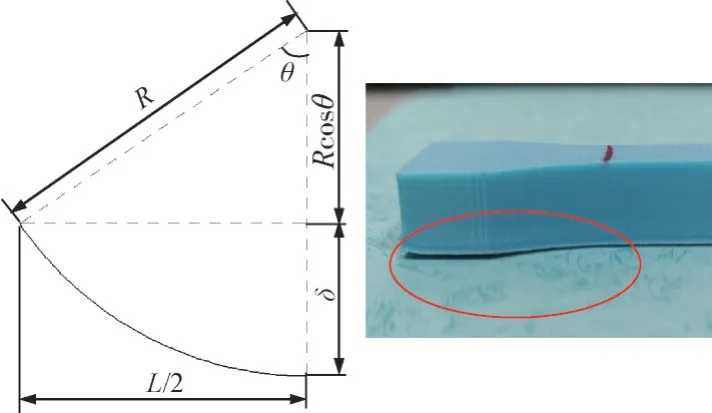
图2 最大翘曲变形量与翘曲半径的关系Fig.2 The relationship between maximum warpage deformation and warp radius

根据余弦函数的泰勒展开式得式（11）：

当L≪2R时，高次项可以忽略；联立式（10）、（11）得δ为式（12）：

通过上述分析发现影响零件翘曲变形的因素主要有加工材料和工艺两方面的因素。具体为材料的线性收缩率、堆积断面长度、Tg等参数，以及工艺方面的堆积层数、Te以及堆积层层厚等。

2 试验验证与结果分析

上一节通过建立FDM 翘曲变形的数学模型分析了影响PLA 制件翘曲变形的因素，由于上述分析模型为理想化模型与实际成型中还存在一定的差别。故有必要通过实验验证翘曲变形数学模型的可行性且进一步探究实际成型过程中FDM的最优参数组合。

2.1 试验设备及材料

本次试验采用的是东莞宏盛达三维科技有限公司生产的“兰度”牌专用3D 打印耗材PLA，材料熔点为190～220 ℃，直径为1.75 mm，Tg为58 ℃，其密度为1 290 kg/m3。实验使用的打印设备是深圳市大昆三维科技有限公司的D160MAX 3D 打印机，如图3所示，喷嘴直径为0.4 mm，打印精度在0.05～0.2 mm之间。

图3 3D打印机Fig.3 3D printer

2.2 实验样件制备与正交实验设计

利用solidworks 软件设计打印零件如图4 所示，其中总长为150 mm，长度为115 mm，边缘宽度为20 mm，中部平行段宽度为10 mm，圆角为70 mm，厚度为10 mm。

图4 打印模型形状和尺寸Fig.4 Shapes and dimensions of the print model

根据式（12），影响翘曲变形的参数主要有分层高度（A），喷嘴温度（B），热床温度（C），和填充率（D），堆积层数（E）和断面长度（F），因此将其作为正交试验的水平因素其中线填充率是考察因素。根据前期调研的结果确定参数的合理取值范围，并制作如表1所示的正交试验因素水平表。为了在后续的函数拟合中得到更精确的拟合曲线，水平数选为5，采用L25(56)的标准正交试验确定最佳工艺参数组合。

表1 正交实验因素和水平Tab.1 Factors and levels of the orthogonal test

本次试验根据上表给出的实验条件打印样件模型。打印结束后，所有样件都在室温中静置5 h，待其自然冷却到稳定状态后，采用精度为0.02 mm 的游标卡尺分别测量零件4 个角点和每条边线的中点处的最大翘曲变形量。测定方法是将样件置于水平平台上，测量从表面到底面的最大厚度，然后减去塑件的基本厚度即为翘曲量。为保证测量的准确性，每个点测量3次，对3次的测量值取平均值，取测量的最大值作为分析的平均值，为保证准确性，最后一位小数为估计值。

2.3 结果与讨论

由正交实验结果可知，翘曲变形量最小值为0.402 mm。因此在所进行的25 组实验中，参数最优组合为A3B3C5D2E4F1，即分层高度为0.2 mm，喷嘴温度为210 ℃，托板温度为55 ℃，填充率为40 %，堆积层数为25，断面长度为20 mm。由于正交实验只是做了全面实验的部分实验，在确定上述实验的最优组合中并没有考虑剩余实验的结果，所以需要对实验数据进行理论分析，并确定上述最优组合是否就是试验的最优组合。

2.3.1 极差分析

极差值描述了各因素对零件翘曲变形量的大小，因素的极差值越大，表示在测量范围内该因素对测量指标的影响值越大。对试验数据进行极差分析，结果见表2。表中ki表示某一因素在i（i=1，2，3）水平时的翘曲变形量算数平均值，可以判断因素的最优水平和各不同因素在i水平的最优组合。

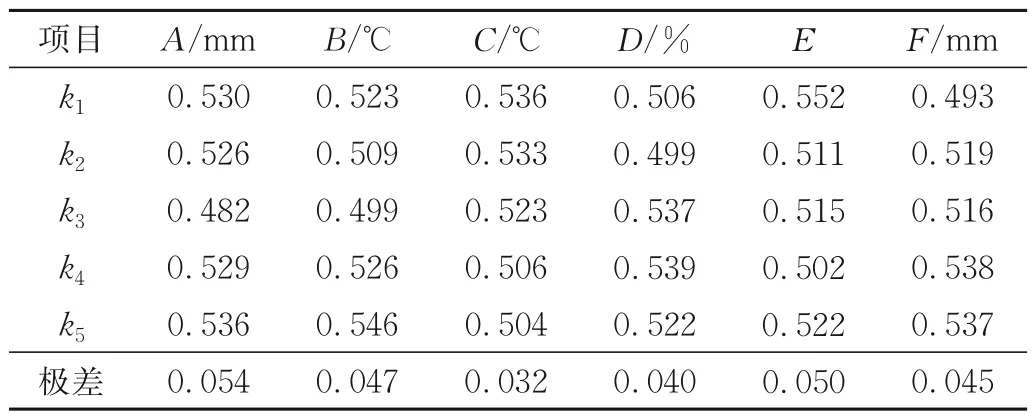
表2 极差分析Tab.2 Range analysis

由表2的分析结果可知，在试验取值范围内可以确定各因素水平对指标影响的主次顺序，对翘曲变形的影响程度从大到小依次为：分层高度、堆积层数、喷嘴温度、断面长度、填充密度、托板温度。其中分层高度和堆积层数对翘曲变形的影响程度较大。同时可以看出，原型的堆积层数是一个重要的影响因素，层数越多翘曲变形量越小，由于在实际成型中制件底层是易发生翘曲的区域，故在加工工艺中可根据零件尺寸适当增加底层层数从而降低制件翘曲变形量。翘曲变形量最优参数组合是A3B3C5D2E4F1，这与试验结果一致。

2.3.2 方差分析

由于在试验过程中试验水平因素引起的数据波动极差分析并不能直观地体现出来，而且不能估计在试验过程中或试验结果中误差的大小。而方差分析可以评价各因素对试验结果影响的显著性，假设误差来源是填充率。采用方差分析来研究各因素对翘曲变形量影响的显著性。表3为方差分析的结果。

表3 方差分析Tab.3 Variance analysis

从上表可以看出，在上述试验条件下，分层高度、喷嘴温度、托板温度、堆积层数、断面长度5个因素的P值分别为0.351、0.495、0.644、0.449、0.445。取显著性水平α=0.05，由于P值均大于0.05，故各因素对翘曲变形的影响都不显著。由表3 中F值可知因素对底部翘曲影响的主次顺序分别是分层高度>堆积层数>喷嘴温度>断面长度>填充率>托板温度。这与极差分析结果一致。

2.3.3 单因素试验结果分析

（1）分层高度对翘曲变形的影响。分层高度即打印每层的垂直尺寸，对零件翘曲量的影响如图5所示。由式（12）理论分析知随着层厚的增加翘曲变形量减小，与曲线前半段很好地对应。在实验范围内，随着分层高度的增加，零件的翘曲量呈先降低后增加的趋势。这是因为在熔融沉积过程中，当分层高度小于喷嘴的直径时，喷嘴对打印物施加轻微的压力，当材料经过喷嘴到打印平台之后，挤压力消失，于是材料内部应力会恢复。因此会出现翘曲变形，分层高度越小，这种压力会越大，所以翘曲变形也就越大。但是随着层高的增加，挤压力虽然变小，但是增加了新增层的冷却时间，新增层底部和顶部的温差会使得材料收缩不均匀，导致样件的翘曲变形量增加，打印质量和精度变差。故在实际应用打印高度设置在0.18～0.22之间比较合适。

图5 分层高度对翘曲变形的影响Fig.5 Effect of layering height on warping deformation

（2）喷嘴温度对翘曲变形量的影响。喷嘴温度对零件翘曲变形的影响如图6所示。由式（12）理论分析可知随着热变形温差的增加翘曲变形量增大。然而在实际成型过程中随着喷嘴温度的增加，零件的翘曲变形量呈先减小后增加的趋势。在210 ℃附近时翘曲变形量较小。这是因为喷嘴温度过低时，丝材熔融不完全，挤出不连续，导致材料的挤压力增大，挤出速度降低，内应力增大。当喷嘴的温度较高时，使得喷嘴挤出的材料偏于液态，降低了材料的黏度，同时会破坏材料的分子结构，增加了挤出过程的控制难度，影响成型件的成型质量。因此在实际成型过程中，喷嘴的温度不能过高也不能过低，在205～215 ℃范围内翘曲变形量最小，质量最佳。

图6 喷嘴温度对翘曲变形的影响Fig.6 Effect of nozzle temperature on warping deformation

（3）托板温度对翘曲变形的影响。托板温度对翘曲变形的影响如图7 所示。这是因为托板温度反应环境温度，当托板温度小于材料的Tg时，随着托板温度与材料熔融温差的缩小，翘曲变形呈近似的线性递减规律变化，这与理论分析模型一致。但是随着托板温度的升高，翘曲变形量不会一直减小。因为随着托板温度的升高，当托板温度大于材料的Tg时，到达托板的材料不能充分凝固，处于高弹态，对新成型层的收缩约束较弱，从而会导致更大的翘曲变形。故在PLA 丝材的成型过程中，一般托板温度取50 ℃。

图7 托板温度对翘曲变形的影响Fig.7 Effect of temperature of bracket on warping deformation

（4）填充密度对翘曲变形的影响。填充密度对翘曲变形的影响如图8所示。由图可知在试验范围内，随着填充密度的增加，零件的翘曲变形量呈先增加后减小的趋势。填充密度较小时，内部支撑较弱，使得外壁冷却收缩时受到内部限制的作用力较小，翘曲变形量较小。随着填充密度的增加，由于材料的层间堆积过程不同步，导致各层体积收缩不同，进而由于内应力不等而产生的翘曲变形量增大。当填充率达到100 %时，模型即为实心模型，虽然可以使样件稳定性增加，翘曲变形量减小，但是喷头就得花过多的时间打印零件的内部结构，耗时耗材，得不偿失。

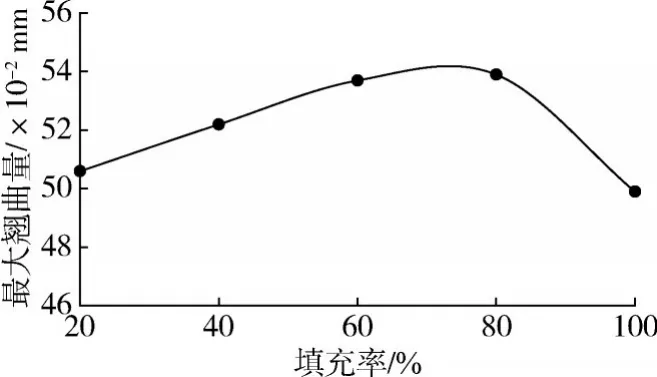
图8 填充率对翘曲变形的影响Fig.8 Effect of filling rate on warping deformation

（5）堆积层数对翘曲变形的影响。从图9中可以看出，随着堆积层数的增加，原型的翘曲变形量呈下降趋势，这一结果与之前关于堆积层数的数学模型相吻合。但随着堆积层数的增加，下降速率逐渐减小，且增大底层成型层数将增加耗材使用量、增大成型时间。故对于成型小型零件时，选择合理堆积层数增加或根据零件尺寸设置底层，可以最大限度地减小模型的翘曲变形量。综合图9 分析得出实际成型过程中取底层填充层数25层为宜。

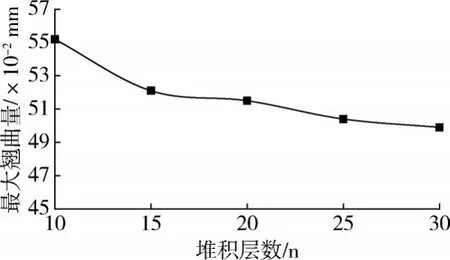
图9 堆积层数对翘曲变形量的影响Fig.9 Effect of accumulation layer number on warping deformation

（6）断面长度对翘曲变形的影响。断面长度对翘曲变形的影响如图10 所示。当断面长度为20 mm 时翘曲变形量最小。形量呈正相关，整体上看，与实验结果完全一致。从图中可以看出，随着断面长度的增加原型翘曲变形量也在增加，但是单位长度线性翘曲量随之减小。因此在堆积成型过程由于制件尺寸一定故应尽量缩短丝材长度的堆积或选择合理的摆放方向以降低成型方向的断面长度。

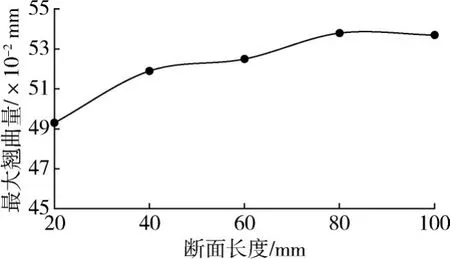
图10 断面长度对翘曲变形量的影响Fig.10 Effect of section length on warping deformation

根据翘曲变形数学模型总结得出了影响制件底部翘曲的主要因素，通过标准正交实验探究得出了FDM各工艺参数对翘曲变形量影响的主次关系及实验最优组合参数。不考虑外观品质等其他因素，参数优化后的模型与标准模式下打印的模型对比如图11 所示，其中图11（a）为标准模式打印下制件两端的翘曲变形，底部翘曲变形较大。图11（b）为参数优化后制件的两端，可以看出底部翘曲变形基本消失。通过试验结果可知优化工艺参数为：分层高度为0.2 mm，打印温度为210 ℃，托板温度为55 ℃，填充密度为40 %，堆积层数为25 层，断面长度为20 mm 可大大减小零件的翘曲变形，验证说明了正交优化分析结论的可行性。