Orientation determination of nitrogen-vacancy center in diamond using a static magnetic field

Yangpeng Wang(王杨鹏), Rujian Zhang(章如健), Yan Yang(杨燕),Qin Wu(吴琴), Zhifei Yu(于志飞), and Bing Chen(陈冰)

Department of Physics,Hefei University of Technology,Hefei 230009,China

Keywords: nitrogen-vacancy centers,polar angle,quantum sensing

1.Introduction

Nitrogen-vacancy (NV) center particularly in the negative charge state in diamond is a promising solid-state system for quantum information processing and quantum sensing,[1–7]which can be initialized and detected by optical pumping.[6,8,9]The electron spin of NV center has long coherence time under ambient conditions.[10]Its electron spin state information can be easily extracted by optically detected magnetic resonance(ODMR) spectra.[9]Its electron spin is sensitive to multiple physical quantities,which makes it possible to be a promising quantum sensor for multiple physical quantities with high sensitivity and spatial resolution,such as electric field,[11,12]magnetic field,[13–16]temperature,[17,18]and crystal strain.[19,20]Accurate and reliable measurement of NV orientation is a crucial step when one attempts to utilize the NV centers for solidstate quantum sensing.

For a single crystal sample,the orientation of the NV axis has four possibilities with knowledge of the crystalline facet in diamond.[21]However, NV centers are randomly distributed in diamond, and their positions and orientations are difficult to identify in the laboratory frame.Therefore, it is necessary to develop a fast and effective method to identify NV orientation for further potential applications.A traditional method to identify NV orientation is to measure ODMR spectra with a series of three-dimensional magnetic fields parallel to theX–Yplane and along theZaxis.[22]Takashimaet al.[23]proposed an improved method that can reduce the measurement time by half.The improved method only needs to measure a single dataset of ODMR spectra by rotating the magnetic field inX–Yplane and a group ODMR spectra of magnetic field in a single direction out ofX–Yplane.These methods are still time-consuming due to measuring plentiful ODMR spectra.For the NV ensembles experiment,the coordinates(X,Y,Z)often consist ofX,Y,andZaxes that are often considered to be along[110],[¯110],and[001]in terms of diamond lattice vectors, respectively.[24]Therefore, the actual orientations of NV axis are still unclear in real space.It is essential to develop a fast and effective method to determine the orientation of the NV axis for quantum sensing based on NV ensembles and single spins in single crystal sample.

In this work, we propose a fast and effective method to simultaneously identify the orientation of four different NV axes assisted with a direction-known magnetic field in the laboratory frame.We just need to measure the ODMR spectra of three different kinds of NV centers and then employ the Nelder–Mead algorithm to calculate the orientation information of NV axis in bulk diamond.Polar angleθand azimuthal angleφare used to describe the orientation of NV axis in the laboratory frame.A directionknown magnetic field with vector orientation (θB,φB) =(50.29◦,78.75◦) is used in the experiment.We finally calculate that the orientation information of four different NV axes is (θNV0,φNV0) = (2.03±0.20◦,287.48±23.04◦) , (θNV1,φNV1) = (110.81±0.48◦,331.57±0.44◦), (θNV2,φNV2) =(107.69±0.27◦,91.30±0.80◦)and(θNV3,φNV3)=(109.97±0.84◦,210.54±0.42◦), respectively.In our approach, owing to only measuring three different kinds of ODMR spectra,the measurement time can be greatly reduced.

In the experiment,ODMR spectra of NV1,NV2,and NV3centers are used to realize the identification of NV orientations,and ODMR spectra of NV0center is employed to verify the experimental results.By comparing the theoretical and experimental results of NV0’s ODMR resonance line, there are deviations of 1.16 MHz and 1.01 MHz with errors of 1.71%and 1.48%,respectively,for left and right resonance peaks of NV0center in the results,which means that our method is effective and accurate.

2.Results and discussion

2.1.Basic properties

The diamond lattice consists of covalently bond carbon atoms that are tetrahedrally bonded to each other through sp3hybrid bonds (distance 1.44 ˚A) with bond angle of 109.47◦.The NV center in diamond is a point defect and consists of a substitutional nitrogen atom and an adjacent vacancy at the diamond lattice as shown in Fig.1(a).In the diamond lattice,there are four kinds of NV centers with different tetrahedral orientations referring to the laboratory frame due to theC3νsymmetry.

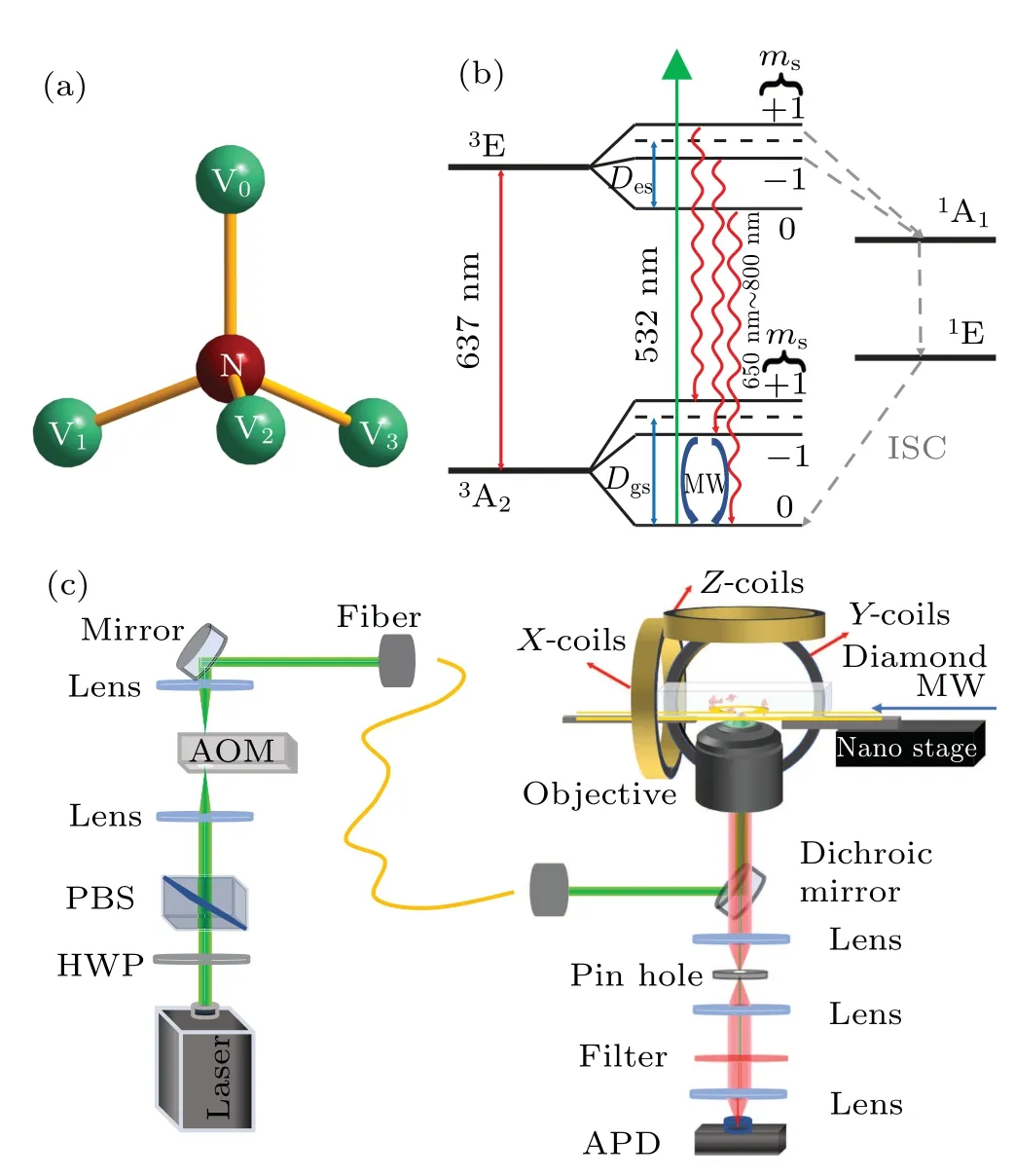
Fig.1.(a)Schematics of the NV center in diamond.NV0,NV1,NV2,NV3 represent tetrahedral orientations for four kinds of NV centers referring to the laboratory frame.(b)Energy-level scheme of the NV center in diamond.The ground state (3A2) and excited state (3E) of NV center are both spin triplets,whose zero-splittings are Dgs=2.87 GHz and Des=1.43 GHz,respectively.Due to the Zeeman effect, the resonance lines between ms =0 and ms=±1 in 3A2 (3E)are separated around 2.87(1.43)GHz in an applied magnetic field.(c) Schematics of the experimental setup with a home-built confocal microscopy.The Gaussian beam is focused on the diamond and the fluorescence photons are collected by oil-immersion microscope objective.MW: microwave, HWP: half wave plate, PBS: polarization beam splitter,APD:single photon avalanche diode.

The electron spin energy levels of the NV center are illustrated in Fig.1(b).Here, 532 nm laser pulse is used to pump the NV center from the ground state3A2to the excited state3E.The NV center’s electron spin can decay from the excited state3E to the ground state3A2by radiative transitions directly or spin-selective nonradiative inter-system crossings(ISC), which can enable optical initialization and readout of the electronic spin state.The electron spin can be manipulated by a microwave field resonant with the transitions betweenms=0 andms=±1 in3A2.

2.2.Experimental setup

The experiment is performed based on a purpose-built confocal microscope system as shown in Fig.1(c), which is employed to address and focus the 532 nm laser beam to the individual NV center.The diamond sample used in the experiment is a type-IIa, single-crystal synthetic diamond(element six).We use an acousto-optic modulator(AOM)to modulate the laser beam and to produce the required laser sequences.The produced laser beam passes through the single mode optical fiber and converts to a near-Gaussian beam.The fluorescence of the NV center can be collected by an oil-immersion microscope objective with NA=1.40 and filtered by pin hole and long pass filter.Finally, the fluorescence photons are detected by a single photon avalanche diode(APD).

2.3.Theoretical analysis

Under external magnetic field conditions,the spin HamiltonianHcan be written as the sum of zero-field splitting term,electron spin Zeeman splitting term, and local strain term in the NV center.His expressed as[25]

whereDgs∼2.87 GHz is zero-field splitting parameter,S=(Sx,Sy,Sz) is the spin matrices of spin-1 systems,µBis the Bohr magneton,geis theg-factor of electron,Bis the external magnetic field andE ∼0 is the strain splitting due to imperfect axial symmetry.Considering that magnetic fieldBhas transverseB⊥[B⊥=(Bx,By)]and axialBzcomponents,and the strain splitting is approximately equal to zero in single-crystal synthetic bulk diamond.The spin Hamiltonian can be written as[25]

andms=0,ms=−1,ms=+1 are the eigenvalues.The spin transition frequencies ofms=0→ms=−1 andms=0→ms=+1 are defined asν1andν2.The transition frequencies are given to the third order in by[26]

wherehis the Planck constant,andαis the angle between the magnetic field and the NV axis.

In experiment,we measure the ODMR spectra and obtain the transition frequenciesν1andν2by fitting resonant peaks with the Lorentzian function.The angleαbetween the magnetic field and the NV axis can be obtained by solving Eqs.(3)and (4).However, it is not enough to identify the orientation of NV axis because the angleαonly tells us that the possible NV orientation is a cone around the magnetic field as depicted in Fig.2(c).

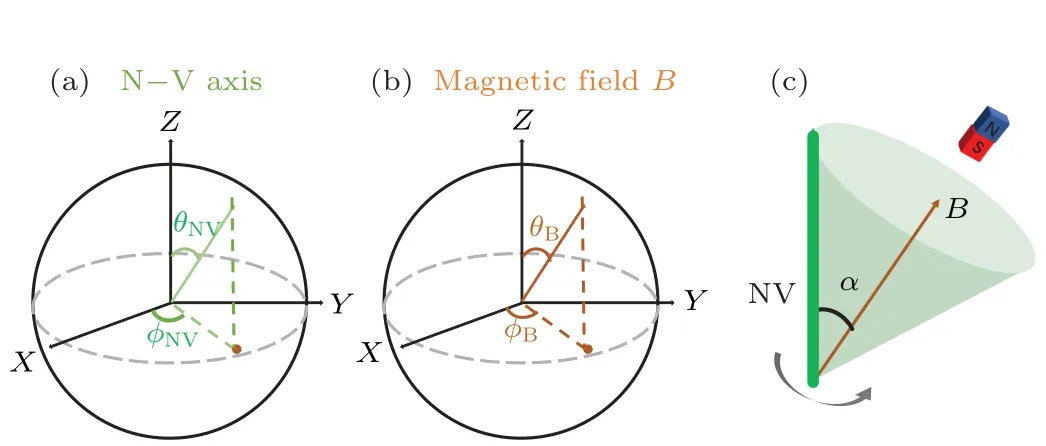
Fig.2.(a) and (b) Orientation of the NV axis NVi = (θNVi, φNVi)(i=1,2,3,4) and the orientation of the magnetic field B =(θB, φB).The brown arrow indicates the direction of the magnetic field, and the green arrow indicates the direction of the NV axis.(c)The possible direction position of NV axis corresponding to single ODMR spectra.In static magnetic field,the orientation of NV axis is possibly located at a conical surface calculated by ODMR spectra.

Here, we define the angle (θNVi,φNVi) (i= 1, 2, 3,4) as the orientation of the NV axis and (θB,φB) as the orientation of the magnetic field in the laboratory frame(spherical coordinates), as shown in Figs.2(a) and 2(b),where the laboratory frame is transformed from the Cartesian coordinate system formed by three-dimensional coils withX-coils corresponding toX-axis,Y-coils corresponding toY-axis, andZ-coils corresponding toZ-axis in real space.Therefore, the orientation of the NV axis can be transformed into the vector NVi= (xNVi,yNVi,zNVi) =(sinθNVicosφNVi,sinθNVisinφNVi,cosφNVi) (i= 1, 2, 3, 4)andB=(xB,yB,zB)=(sinθBcosφB,sinθBsinφB,cosφB)in these Cartesian coordinates.In diamond lattice, the relationship between the NV axial vector and the magnetic field vector can be given as follows:

where NVi, NVj(i,j=0, 1, 2, 3 andi／=j),αk(k=1, 2,3) represent the angles between the NV axis (NV1,NV2, and NV3)and the magnetic fieldB,as shown in Fig.1(a)).Based on Eqs.(5) and (6), we are able to calculate the final values of the four NV orientations using the Nelder–Mead algorithm and obtain the angleα.

The Nelder–Mead algorithm is one of the best known algorithms for multidimensional unconstrained optimization without derivatives.For then-dimensional minimization problem minf(x), with a simpler description, the method for searching the minimum value is described as follows:(i) Generate initial valuesxl(l= 2,3,...,n+1) next tox0we give.(ii) Find minimum pointxmin thef(xl).(iii)Takexmas the new initial value, and repeat steps (i) and(ii) until local minimum appears.The constraint equation is minf(x) ==1(NVk·B −cos(αk))2+=1(NVk·NV0−cos(109.47◦))2+=2(NVk·NV1−cos(109.47◦))2+=3(NVk·NV2−cos(109.47◦))2, whereαkis the the angles between the NV axis and the magnetic field as shown in Eqs.(5) and (6), and NVkis the results of each search.In the experiment, first the initial value with four NV axis’parameters is randomly given, considering the internal bond angle (109.47◦) of diamond crystal.Because the search result of the Nelder–Mead algorithm is the local minimum,some initial values with large numerical differences are given to find the absolute minimum of the equation minf(x).Then angles of first initial value are rotated fort(t=30◦,60◦,90◦,120◦,150◦,180◦)around theY-axis to produce a series of new initial values by rotation matrix.[27]Later,when a series of initial values are applied, the local minimum can be searched by the Nelder–Mead algorithm.Finally,when the absolute minimum appears,the NVkis the final search result.

2.4.Results

In the experiment,four kinds of NV centers close to each other(several microns)are selected through the difference of ODMR spectra.In the confocal microscope system the positions of laser focus and oil-immersion microscope objective are fixed.Therefore,the different NV centers in diamond can be moved to the same laser focus by nano-piezoelectric stage in order to ensure that each NV center is under the same magnetic field.Then, we sweep the microwave (MW) frequency and obtain the ODMR spectra.Compared to the continuous ODMR scheme, the pulsed ODMR scheme with a resonant MWπ-pulse and a read-out laser pulse can reduce the power broadening of ODMR spectra and improve spectral resolution.At low MW power (π-pulse duration of∼2600 ns), we can observe the hyperfine splitting in the ODMR spectra due to the hyperfine interaction between electronic spin and nitrogen nuclear spin.Four sets of pulsed ODMR spectra are measured in a[111]-oriented bulk diamond with the certain static magnetic field as shown in Fig.3.The transition frequencies of left peak (ms=0,mI=−1→ms=−1,mI=−1), middle peak(ms=0,mI=0→ms=−1,mI=0)and right peak(ms=0,mI=+1→ms=−1,mI=+1) in the ground state3A2are same.For convenience, the middle peaks (ν1andν2) are selected and correspond to the transition frequencies ofms=0,mI=0→ms=−1,mI=0 andms=0,mI=0→ms=+1,mI=0,which are shown in Table 1.

Table 1.The transition frequencies for NV centers in different orientations.The angles α between the static magnetic field and the NV axis are extracted from the ODMR spectra of NV1 center,NV2 center,and NV3 center as shown in Fig.3.The last column is the final orientations of NVi (i=0,1,2,3)shown in Fig.4(b).

According to the ODMR spectra shown in Fig.3,the angleαbetween the magnetic fieldBand the NV axis is calculated by Eqs.(3) and (4), and three different cones (NV1:light green, NV2: light yellow, NV3: nattier blue)around the magnetic field vector that are the possible orientations of NV1axis, NV2axis and NV3axis as shown in Fig.4(a).By using the Nelder–Mead algorithm for Eqs.(5) and (6), we can calculate the results NV0= (2.03±0.20◦,287.48±23.04◦)(red), NV1= (110.81±0.48◦,331.57±0.44◦) (green),NV2=(107.69±0.27◦,91.30±0.80◦) (yellow) and NV3=(109.97±0.84◦,210.54±0.42◦) (blue) shown in Fig.4(b)and Table 1.In order to verify the accuracy of the results,the theoretical transition frequencies of the fourth kind of NV center (NV0) are calculated as NV0L(ν1) = 2807.704 MHz and NV0R(ν2) = 2941.211 MHz by Eqs.(3) and (4).This formula±The experimental measured values ofν1andν2for NV0are equal to 2806.54±0.16 MHz and 2942.22±0.16 MHz as shown in Table 1.We find that there are deviations of 1.16 MHz and 1.01 MHz with errors of 1.71% and 1.48%, respectively, between the theoretical and experimental results for left and right resonance peaks of NV0center.The deviation may come from strain of lattice and temperature fluctuation during measurement process.

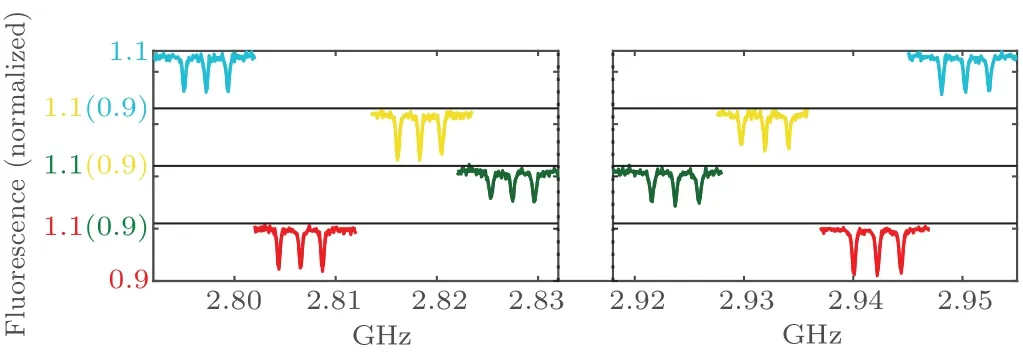
Fig.3.ODMR spectra for NV centers in different orientations.In the static magnetic field,different NV centers have anisotropic Zeeman splitting and ODMR spectra.Because of hyperfine interaction with the electron spin and 14N nuclear spin, the transitions between ms =0 and ms =±1 both have three peaks,respectively.These solid broken line and curve(red,green,yellow,and nattier blue)represent the experimental data and the data of fitting using Lorentzian functions for NVi center(i=0,1,2,3).

In Table 1, the azimuth (φ) error of NV0is relatively large.The polar angleθNV0of NV0axis is close to zero,which almost coincides with the direction of the north pole.Around the north pole,the azimuth angle is completely uncertain.The orientation error of four kinds of NV centers are less than 0.93◦.

Fig.4.(a) Possible orientation of the NV axis.The angles α between the magnetic field B and the NV1−3 axis are 116.64◦(light green), 58.15◦(light yellow), and 135.44◦(nattier blue), respectively,showing that the possible NV axis is a cone around the magnetic field vector.(b) Four orientation of NV axis calculated with the Nelder–Mead algorithm.The calculated NV axis results are NV0 =(2.03±0.20◦,287.48±23.04◦)(red),NV1=(110.81±0.48◦,331.57±0.44◦)(green), NV2 =(107.69±0.27◦,91.30±0.80◦) (yellow) and NV3 =(109.97±0.84◦,210.54±0.42◦)(blue).

3.Conclusions

In summary, we propose and demonstrate an efficient method to simultaneously identify four types of NV axis information with a direction-known magnetic field in a bulk diamond.Our method only needs to measure a set of ODMR spectra and then extract the polar angle of each NV center and magnetic field.Combining with the polar angle information of different NV centers, we finally employ the Nelder–Mead algorithm to calculate the orientation information of NV axis.Our method is fast and effectively to determine the orientation of the NV axis for ensembles and single spins in single crystal samples.This method can be directly extended to the orientation determination of NV centers in a micro-diamond,and easily applied in quantum sensing of vector magnetic and electric fields in the future.

Acknowledgements

This work was supported by the National Key R&D Program of China (Grant No.2020YFA0309400), the National Natural Science Foundation of China (Grant No.12174081),and the Fundamental Research Funds for the Central Universities(Grant Nos.JZ2021HGTB0126 and PA2021KCPY0052).