一种近似解析的再入滑翔飞行器可达域快速生成方法

李兆亭,周 祥,张洪波,汤国建

国防科技大学空天科学学院,长沙 410073

0 引言

再入滑翔飞行器的可达域是指在满足过程约束条件下,飞行器从初始状态出发,能够到达着陆或者交班状态下所能允许的区域范围。它综合反映了飞行器的纵向机动能力与横向机动能力,体现了飞行器的整体机动性能。可达域的求解可为飞行器轨迹规划与制导、应急着陆点选择、制导律性能评估提供依据,具有重要意义。

可达域求解方法依赖于轨迹规划方法的发展。在基于经典的剖面轨迹规划方法研究条件下,发展得到了若干种可达域求解方法[1-3]。如He等[4]推导得到一个具有不确定性效应的再入走廊,其中攻角剖面可调节,纵向阻力剖面设计为上、下拟合安全边界的插值结果,横向升力-阻力剖面则利用准平衡滑翔条件得到,最后通过比例积分微分(PID)跟踪器来跟踪剖面,得到可达域。同时,随着优化算法的成熟与发展,具有剖面形式的轨迹规划问题亦可通过相关的优化算法进行规划求解,如梁巨平等[5]选取倾侧角为时间的分段常值函数,采用遗传算法来求解一系列的轨迹优化问题。王涛等[6]提出一种基于Gauss伪谱法的再入可达域计算方法,采用固定的攻角剖面,仅对倾侧角进行单变量寻优。

此外,还有一些研究者打破了剖面假设、拟平衡滑翔假设等藩篱,设计了其他类型的可达域求解方法,如基于虚拟目标点[7]、基于直接法[8-11]等。相比基于剖面的求解方法,这些新方法不需要设计相关剖面,其可达域范围更大且更接近实际值。如蔺君等[12]对攻角、倾侧角进行参数化,利用带约束的差分进化算法求解满足再入过程约束和终端约束的再入轨迹。章吉力等[13]对考虑禁飞区条件下的空天飞机再入可达区域问题进行研究,并基于极限绕飞轨迹提出一种不限禁飞区位置的可达区域求解方法。吴楠等[14]基于平衡滑翔假设和最优化飞行准则,通过数值积分获得最大纵程和横程弹道,基于椭圆近似法利用3个末端点构建可达域椭圆边界。

在基于直接法的可达域计算方法中,伪谱法由于具有良好的适用性和强大的求解能力成为其中一类重要的方法。如岳彩红等[15]基于改进高斯伪谱法对高超声速变形飞行器再入可达域进行了求解。Wang等[16]在准平衡滑行条件下,使用高斯伪谱法计算得到了返回航天器的可达域。此类可达域计算方法通常将可达域计算归结为两类问题,即最大/最小纵程轨迹规划问题和给定纵程下的最大/最小横程轨迹规划问题。

本文借鉴了上述基于直接法的可达域计算思路,针对描述可达域的极值轨迹规划问题,利用极大值原理推导出攻角应为当前最大升阻比攻角的相关推论,并仿真验证了该推论的有效性。其次设计了给定纵程下不同横程极值轨迹的倾侧角变化规律,并通过梯度下降的优化方法计算得到相关参数。最终,提出了一种近似解析的可达域求解方法,并通过仿真验证了所提方法的有效性。

1 再入动力学模型及其约束

在进行可达域的求解时,将飞行器的运动转换到换极坐标系[17]中描述。在换极坐标系中,再入飞行器起点的经纬度均为0,终点的经度和纬度分别描述了再入纵程和再入横程。利用这些特性,可方便地标定经纬度等参数的变化范围,简化弹道规划算法。

在换极坐标系下,可以推导得到飞行器再入运动方程,如下:

(1)

(2)

其中:ρ为大气密度,M为飞行器质量,S为参考面积,CL和CD分别为升力系数和阻力系数,均与攻角α有关。

同时,再入飞行中还需考虑多种过程约束,如热流密度约束、过载约束、动压约束等,如式(3)所示。

(3)

本文中,仿真所用的目标飞行器为CAV-H,其相关参数和气动数据可以参考文献[18]。

2 极值轨迹规划问题最优特性分析

将可达域求解的两类轨迹统称为极值轨迹,意在说明该轨迹在纵、横程方面具有的最优性。同时将两类轨迹规划问题统称为极值轨迹规划问题。

为降低推导的复杂度,本节中轨迹优化问题暂不考虑热流、过载、动压等约束。

2.1 最大纵程轨迹规划问题

对于该问题而言,其升力几乎全部用于纵向的调整,无侧向机动,因此不妨令倾侧角始终为0。同时,假设θ为小角度,忽略地球自转项。在这些假设条件下,最大纵程轨迹优化问题就等价于最大路程轨迹优化问题。

记飞行器在横向平面内的路程为S,则有:

(4)

与公式(1)中的有关式子联立,假设θ为小量,并忽略二阶小量,可得:

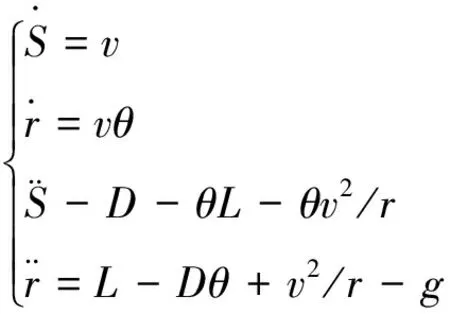
(5)

可将上述最大纵程轨迹优化问题近似转化为问题P0,如下所示:

(6)

利用极大值原理求解上述问题P0的最优性条件。其哈密顿函数为:

(7)

其极值条件为:

(8)

关于控制量的部分取为极小,有:

(9)

考虑到控制量u1、u2为飞行器的升阻力加速度,应当满足一定的关系式,有:

u1=ku2

(10)

式中:升阻比k在不同速度和攻角下为不同的值。此时控制量只有攻角。

将θ=x4/x3代入,则式(9)转化为:

u1(λ4-λ3θ)-u2(λ4θ+λ3)

(11)

考察CAV-H飞行器的气动情况,如图1所示。飞行器的升阻比随攻角具有相同的变化规律。其升阻比总是从A点的最小攻角开始,逐渐增大至B点的当前最大升阻比攻角,而后逐渐减小,直到端点C。

图1 不同速度、高度下的升阻比随攻角变化

(12)

因此不妨对式(11)分情况讨论:当攻角位于AB段时,因参数(λ4-λ3θ)和(λ4θ+λ3)值大小的不同,其极小值一般取为A点或B点。当攻角位于BC段时,其极小值一般取为C点或B点。因此,最大纵程轨迹的攻角应为最大攻角、最小攻角和当前最大升阻比攻角三者之一。

2.2 给定纵程下的最大/最小横程轨迹规划问题

引入θ小角度假设,忽略地球自转项,则给定纵程下的最大横程轨迹规划问题P1可以描述为式(12),式中λe为给定的纵程。而对于最小横程问题而言,其性能指标取为J=φ(tf)+(λ(tf)-λe)2,其他完全一致。

求解问题P1的最优性条件,其哈密顿函数为:

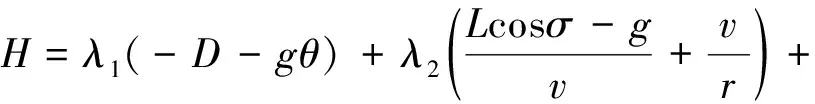
(13)

其极值条件为:

(14)

提取关于控制量的部分,并记有,

(15)

则应当取极小值的部分为:

(16)

当ε+σ=-π/2+2kπ,k=0,1,…,N时,式(16)进一步转化为:

(17)

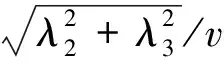
2.3 结论验证

综上所述,对于这两类极值轨迹规划问题而言,其攻角应为最大攻角、最小攻角和当前最大升阻比攻角三者之一。

为检验上述结论的有效性,采用伪谱法对飞行器的可达域进行求解。采用两个算例进行换极坐标系下可达域求解,算例1的初始高度为60 km,算例2的初始高度为65 km,两个算例的初始速度均为6.5 km/s,初始速度倾角均为0°,终点速度要求大于1 km/s,终点速度倾角的大小不做限制要求,终点高度为30 km。

不同算例下各条极值轨迹的升阻比如图2所示。在图2中,短划线代表当前最大升阻比,点虚线代表最小攻角的升阻比,下方的点划线代表最大攻角的升阻比,上方的实线代表伪谱法规划结果的升阻比。

图2 不同算例下各极值轨迹的升阻比变化情况

可以看出,不同算例下飞行器的各极值轨迹几乎总是沿着当前最大升阻比攻角前进。除了开始时刻和终端时刻略有差别。这种差别可能由于优化方法中一些终端状态约束设置的不同引起。

从物理意义上,阻力代表了机械能的损耗速率。升力则有助于飞行器的上升,可增大速度倾角,使高度减小速率变缓甚至高度增加,从而增加纵程。从动力学角度来说,高度越高,阻力越小,也会使得机械能损失速率减小。那么,升阻比就代表了损失相同机械能的条件下,飞行器获得的纵程增益。升阻比小意味着其纵程增益小,当升阻比为0时,其纵程增益为0,该运动退化为一个具有阻力加速度的抛物运动。显然,对于构成可达域边界的每一条轨迹,选择一个最大升阻比攻角,无疑是一个最优的选择。

因此,在计算可达域的极值轨迹时,不妨直接令攻角为当前最大升阻比攻角,积分到期望状态条件,可以得到一条近似的极值轨迹。

3 近似解析的再入可达域生成方法

对于最大纵程轨迹规划问题,可以以当前最大升阻比攻角和0倾侧角积分得到其轨迹。但对于给定纵程下的最大/最小横程轨迹规划问题而言,还需得到倾侧角的变化规律。

3.1 倾侧角近似与参数计算

倾侧角难以直接计算得到,在2.2节的分析中可知,其与拉格朗日乘子λ2和λ3直接相关,而拉格朗日乘子的估计一直是优化求解的难题。这里,考虑到文献[19]中可达域的求解结果,其倾侧角的变化非常有规律,因此不妨直接设计倾侧角的变化规律,以得到近似的可达域。

设计不同极值轨迹的倾侧角随时间的曲线为不同斜率、不同初值的直线。直线的起点为不同的初始倾侧角,直线的斜率为常值,直线的终点为0。直线的起点,即初始倾侧角一般取为90°i/N,i=1,…,N,N为给定纵程下最大横程轨迹的数目。第i条轨迹的斜率ki按照如下给定:

ki=(i-1)(kmax-kmin)/(N-1)+kmin

(18)

其中:kmax为最小纵程轨迹倾侧角变化的斜率,kmin为次最大纵程轨迹倾侧角变化的斜率。

对应的倾侧角变化规律为:

σ=90°i/N+kit

(19)

最小纵程轨迹对应的倾侧角变化规律为:

(20)

最大纵程轨迹对应的倾侧角变化规律为:

σ=0, 0≤t≤tmax

(21)

其中:tmax可通过令倾侧角为0并以当前最大升阻比攻角进行动力学积分得到。tmin可以通过求解倾侧角符合上述变化规律的最小纵程问题得到。tmin的详细求解流程如下所示:

1) 给定一个tmin的估计值t0;

2) 令tmin=t0和tmin=t0+10,并积分计算2种情况下的纵程,计算纵程对于tmin的梯度g,寻优方向为负梯度方向-sgn(g);

3) 回溯直线搜索方法确定寻优步长Δt,计算得到参数tmin=tmin-sgn(g)Δt;

4) 如果寻优步长小于某一阈值ε,即Δt≤ε,则停止,并输出tmin;否则令t0=tmin,进入步骤2)。

如上所述,在求解得到参数tmax和tmin后即可确定kmax和kmin,则通过式(18)、(19)可以得到任意一条最大横程轨迹的倾侧角变化率。其给定纵程下最小横程轨迹的倾侧角变化规律与最大横程一致,但符号是相反的。

3.2 近似解析的可达域生成方法

最终,形成了一种可达域的近似解析求解方法。在此方法中,最大纵程轨迹通过令倾侧角为0,以当前最大升阻比攻角进行动力学积分得到。给定纵程下的最大最小横程轨迹,通过以设计的倾侧角变化规律和当前最大升阻比攻角进行动力学积分得到。其流程如图3所示。

图3 一种近似解析的可达域计算流程

如图3所示,首先以0倾侧角和当前最大升阻比攻角积分得到最大纵程轨迹,并得到最大飞行时间tmax。然后以式(20)所示的倾侧角变化规律和当前最大升阻比攻角进行积分,并利用3.1节所述的优化方法计算得到最小飞行时间tmin。最后以式(18)、(19)所述的倾侧角变化规律和当前最大升阻比攻角进行积分,得到一侧的极值轨迹。改变倾侧角的符号,积分得到另一侧的极值轨迹,即可形成再入飞行器的可达域。

4 仿真校验

为验证所提方法的有效性,本节选取3个不同的飞行器起点状态,分别利用所提方法和伪谱法计算得到各自的可达域。将得到的两组结果作为对比,验证本文所提方法的有效性和合理性。

可达域计算的参数设置如表1所示。在表1中,3个起点状态被分别赋予了不同的速度与高度值,期望的终点速度大于1 km/s,期望的终点高度在10 km～30 km之间,同时不对终点的速度倾角做限制。得到的可达域近似结果如图4所示。

表1 不同算例下的可达域求解参数设置

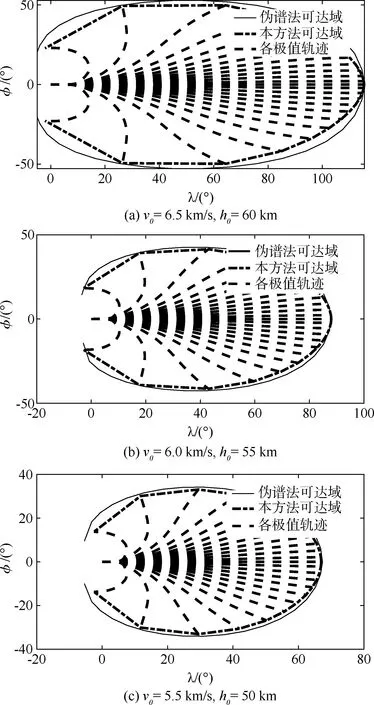
图4 可达域计算结果对比

图4给出了不同起点状态下的可达域计算结果。其中实线代表伪谱计算得到的可达域边界,点划线代表由本方法计算得到的可达域边界,虚线为由本方法计算得到的各条极值轨迹。可见相对于伪谱法计算的结果,本方法得到的可达域与之极为接近,仅存在较小的差异。

同时,考虑到如图3所示的可达域计算流程,主要包含了参数tmin的优化求解、极值轨迹的积分等过程。且参数tmin的优化求解也仅仅借助于积分运算与梯度下降算法,因此对于整个求解过程而言,其不包含复杂的优化计算过程,具备工程试验的可操作性。

5 结论

针对再入滑翔飞行器的可达域计算问题,提出一种近似解析的可达域计算方法。首先针对2类极值轨迹优化问题进行了相关推导,指出无论是最大纵程轨迹优化问题,还是给定纵程下的最大/最小横程轨迹优化问题,其攻角应当是当前最大升阻比攻角。通过仿真验证了上述推论的有效性。然后针对性地设计了各条极值轨迹的倾侧角变化规律,给出了最终解析近似的可达域生成方法流程。最后通过与伪谱法计算得到的可达域的对比,验证了本文所提方法的有效性。