水下爆炸仿真参量设置影响研究
2023-09-03吉耿杰魏继锋
周 超,吉耿杰,魏继锋
(1. 92228部队, 北京 100072;2.北京理工大学 爆炸科学与技术国家重点实验室, 北京 100081)
0 引言
水中爆炸载荷及其特性研究是水下爆炸技术领域研究的核心,对水下爆破技术应用具有重要意义。早在1948年,Cole就根据大量的水下爆炸试验,分析了水下爆炸过程中的基本物理现象、水下爆炸载荷传播特性,并提出半理论半经验计算公式[1]。在此基础上,Zamyshlyayev研究了冲击波在自由液面及水底的强非线性效应[2]。而在气泡载荷方面,在考虑了流体的可压缩性后,Prosperetti[3]和Lezzi[4]给出了气泡动力学一阶理论模型和二阶理论模型。基于气泡动力学方程以及试验数据,学者们给出计算气泡脉动参量的经验公式,例如,Swift等[5]给出了计算TNT和特屈儿爆炸气泡最大半径及脉动周期的经验公式;Slifko[6]给出了适用于计算远场二次压力波正压持续时间和冲量的经验公式;Van Aanhold[7]给出了计算气泡在第一个脉动周期内铅直位移、气泡能量损失的经验公式。王振宇等[8]根据一维不可压缩流体力学理论,建立了水下爆炸气泡脉动规律和水中压力分布规律的基本方程,并引入虚拟力和气泡能对方程进行了改进。
由于水下爆炸试验耗资巨大且测试困难,数值仿真技术已成为研究其的重要手段。数值仿真是研究水下爆炸载荷的重要方法之一。常见的数值方法包括有限差分法[9-11]、有限体积法[12-13]、有限元法[14-15]和SPH法[16]等。Barras等[17]运用ALE法对空间收敛性、水域尺寸和边界效应对爆炸气泡的影响进行了研究;Hao Huang、刘科种、丁宁、方斌等[18-21]对网格密度、状态方程、人工粘性系数对水下爆炸冲击波载荷特性的影响进行了研究,但仅仅是定性描述;辛春亮等[22]采用了ALE和Euler算法,发现网格尺寸及网格质量对模拟近场水下爆炸的计算结果影响很大。Sang-GabLee[23]仿真研究了舰船在水下爆炸载荷作用下的动态响应,探讨了流体网格尺寸、流体边界形状、自由表面尺度等一些重要参数的选取对计算结果的影响。
本文中拟运用AUTODYN软件研究水下爆炸载荷特性,分析数值仿真参数设置对水下爆炸气泡脉动与冲击波载荷计算的影响,提出数值模拟时水域尺寸及网格尺寸的取值方法,并与已有实验数据对比以验证其准确性,以期为水下爆炸研究提供技术基础和分析依据。
1 水下爆炸载荷理论计算方法
水下爆炸载荷研究主要是指冲击波和气泡脉动载荷的研究。
1.1 冲击波载荷
Cole基于大量水下爆炸实验结果拟合出了水下爆炸载荷参量计算公式,Zamyshlyayev在此基础上做了进一步细化。TNT炸药水下爆炸冲击波峰值压力随爆距和药量的变化公式为

式中:r为爆距,m;W为药量,kg;r0为半径,m。
Zamyshlyaev提出的衰减常数为
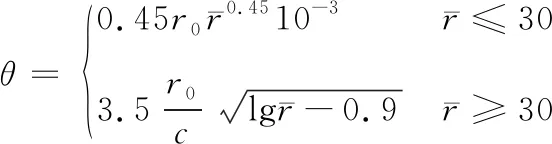
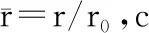
水下爆炸冲击波是一种宽频波,没有固定的波长。但工程应用中,指数波的衰减常数是一个重要的时间特征参数,是优势波分量的周期,通常以其作为冲击波的周期,对应的波长就定义为冲击波的波长。单元网格的粗细与波长密切相关[24],因此,单元尺寸须慎重选择。采用一个冲击波波长内的网格数量λ=cθ/d,作为网格密度的特征参量,研究其对冲击波压力峰值的影响。
1.2 气泡脉动载荷
Cole提出的TNT炸药气泡最大脉动半径与脉动周期计算表达式为
Rmax=3.383W1/3/((h+9.8)1/3)
Tmax=2.064W1/3/((h+9.8)5/6)
式中:Rmax为最大气泡半径,m;Tmax为脉动周期,s;h为爆炸水深,m。
2 数值仿真模型
2.1 模型构建方法
采用一维楔形网格构建水下爆炸计算模型,单位为mm-mg-ms,炸药为球形装药,如图2所示。爆心设于原点即炸药中心,炸药和水均采用Euler网格剖分。
2.2 状态方程
水采用多项式状态方程,通过改变比内能来改变静水压力,从而改变水域深度。当水压缩时,水的状态方程为
p=A1μ+A2μ2+A3μ3+(B0+B1μ)ρ0e,μ>0
当水拉伸时,水的状态方程为
p=T1μ+T2μ2+B0ρ0,μ<0
式中:μ为压缩比,μ=ρ/ρ0-1;A1、A2、A3、B0、B1、T1、T2为材料常数;e为水的比内能,e=(p0+ρ0gh)/B0ρ0。水的状态方程参数如表1所示。
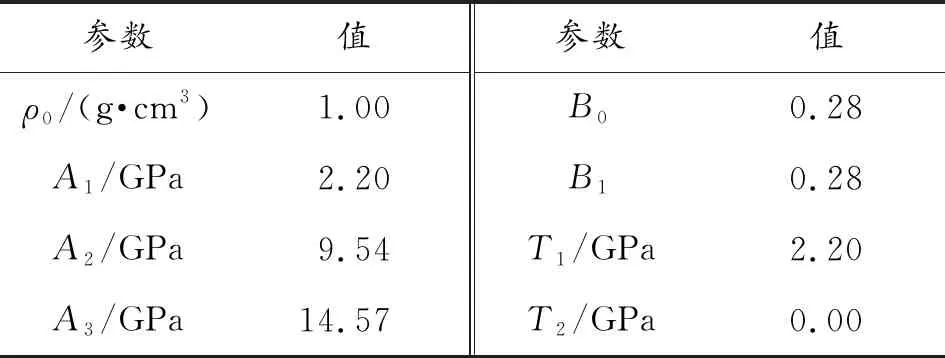
表1 水的状态方程参数
TNT炸药采用JWL状态方程
式中:V为相对比容;E为单位体积内能;A、ω、R1、B、R2为材料参数。具体参数如表2所示。
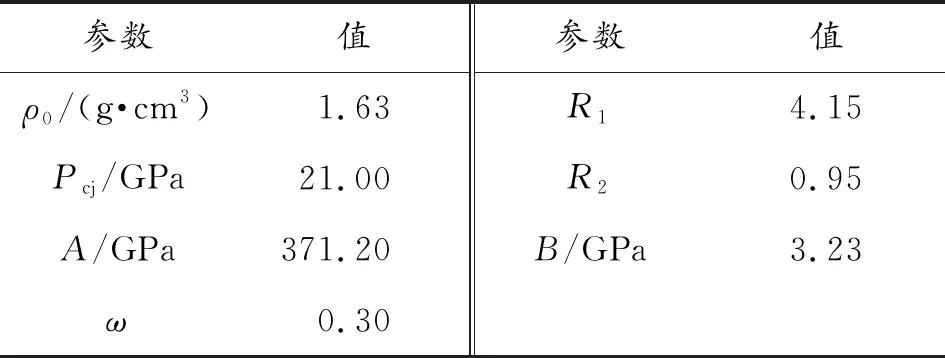
表2 TNT炸药的状态方程参数
3 数值仿真参数设置
3.1 边界条件的选择
采用一维楔形网格建模进行水下爆炸计算时,不同边界条件对冲击波特性基本无影响,对气泡脉动特性影响较大,有些学者选择flow-out边界条件模拟无限水域,也有选用transmit边界条件[25-27]。
这里分别选用transmit、flow-out和None边界条件,静水压力为0.1 MPa,分析1 g TNT球形炸药、水域大小为1 m水下爆炸计算时,边界条件对气泡脉动的影响,计算结果如表3所示。

表3 边界约束的选择
由表3可以看出,采用flow-out与None边界条件时得到的气泡脉动特性完全一致,说明flow-out边界条件在一维楔形网格计算中不起作用;采用transmit边界条件计算得到的气泡脉动特性与理论值也有较大偏差,因此该边界条件也不够准确。在实际计算中,应设置足够大的水域来模拟无限水域环境,从而减少水域边界反射对气泡脉动特性的影响。
3.2 水域尺寸的影响
水域尺寸对冲击波载荷影响小,对气泡脉动载荷影响大,在此研究水域尺寸对气泡脉动半径的影响十分必要。在1 g药量TNT下,水域尺寸分别为1、2、5、10 m,将水域尺寸与装药半径之比作为横坐标,得到的气泡脉动特性曲线与理论对比如图3所示。可以看出,气泡半径与气泡脉动周期随着水域尺寸的增大呈幂指数增长趋势,在600倍装药半径之内增长比较迅速,之后趋于平稳,综合准确度与计算量,在本装药条件下水域尺寸选择1 200倍装药半径较为适合。
3.3 网格密度对冲击波特性的影响
改变网格密度,研究1 g球形TNT装药在测点0.388 m处的冲击波特性,波形曲线如图4所示。可以看出:随着网格密度的增大,冲击波压力上升为迅速,冲击波压力峰值更高,且波形下降更加平缓。
1) 不同比例距离冲击波压力峰值的影响。
对于1 g球形TNT装药,在不同网格密度时,各观测点得到的冲击波压力峰值结果如图5所示。随着特征参量的增大,各测点处的冲击波压力峰值均成指数增大趋势,在100 内迅速增加,在100 后逐渐平稳并保持不变。根据理论经验公式,250、500、750、1 000 mm处的冲击波压力峰值分别为18.61、8.50、5.38、3.88 MPa。仿真值与理论值相比误差小于5%,说明仿真模型计算可靠。
取各网格密度下冲击波压力峰值与最小网格尺寸下冲击波压力峰值的相对误差Er,得到结果如图6所示。可以看出随着网格密度的增大,不同爆距处的峰值压力误差均呈减小趋势,且爆距越小,误差越小,网格密度对冲击波峰值压力的影响越小,计算结果越准确。
对上图平滑后取5%误差与10%误差点拟合得到图7,横坐标为比例距离Z=r/W1/3:
由此得到了5%误差和10%误差时最小网格密度随比例距离变化的取值公式:
5%误差时的拟合方程:λ=84.35+4.168 97Z
10%误差时的拟合方程:λ=44.045+2.401 96Z
2) 某比例距离下不同药量时的冲击波压力峰值。
观测点取相同比例距离,TNT药量取1、10、100、1 000 g,研究网格密度对冲击波压力峰值的影响,结果如图8所示。可看出不同药量相同比例距离得到的冲击波压力峰值基本一致,且随着网格密度的增加而增大。
对比压力峰值的相对误差,结果如图9所示。
取5%误差与10%误差点如图10所示。横坐标为炸药药量,纵坐标λ。由此图可以看出,炸药药量在相同比例距离时对于网格密度变化造成的冲击波压力峰值计算误差影响很小,因此,综合之前得到的5%误差和10%误差时相同药量不同比例距离网格尺寸最小取值计算公式,可以得到AUTODYN计算TNT装药水下爆炸时考虑计算精度的网格尺寸最小取值计算公式为
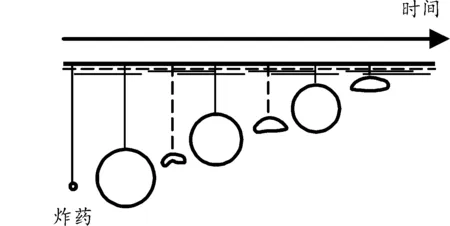
图1 气泡脉动示意图

图2 一维深水爆炸仿真模型

图3 气泡脉动特性变化规律
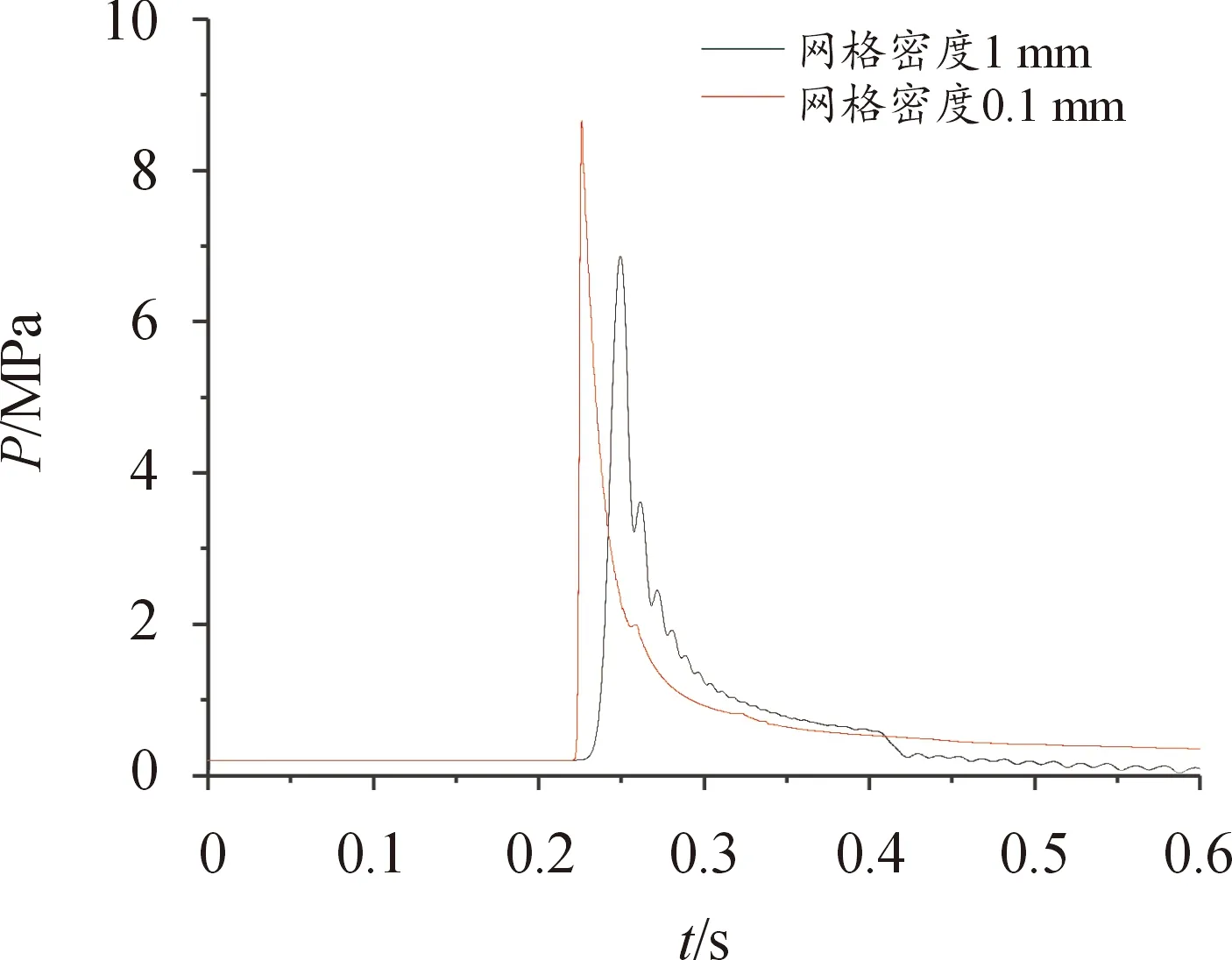
图4 不同网格密度下的冲击波波形
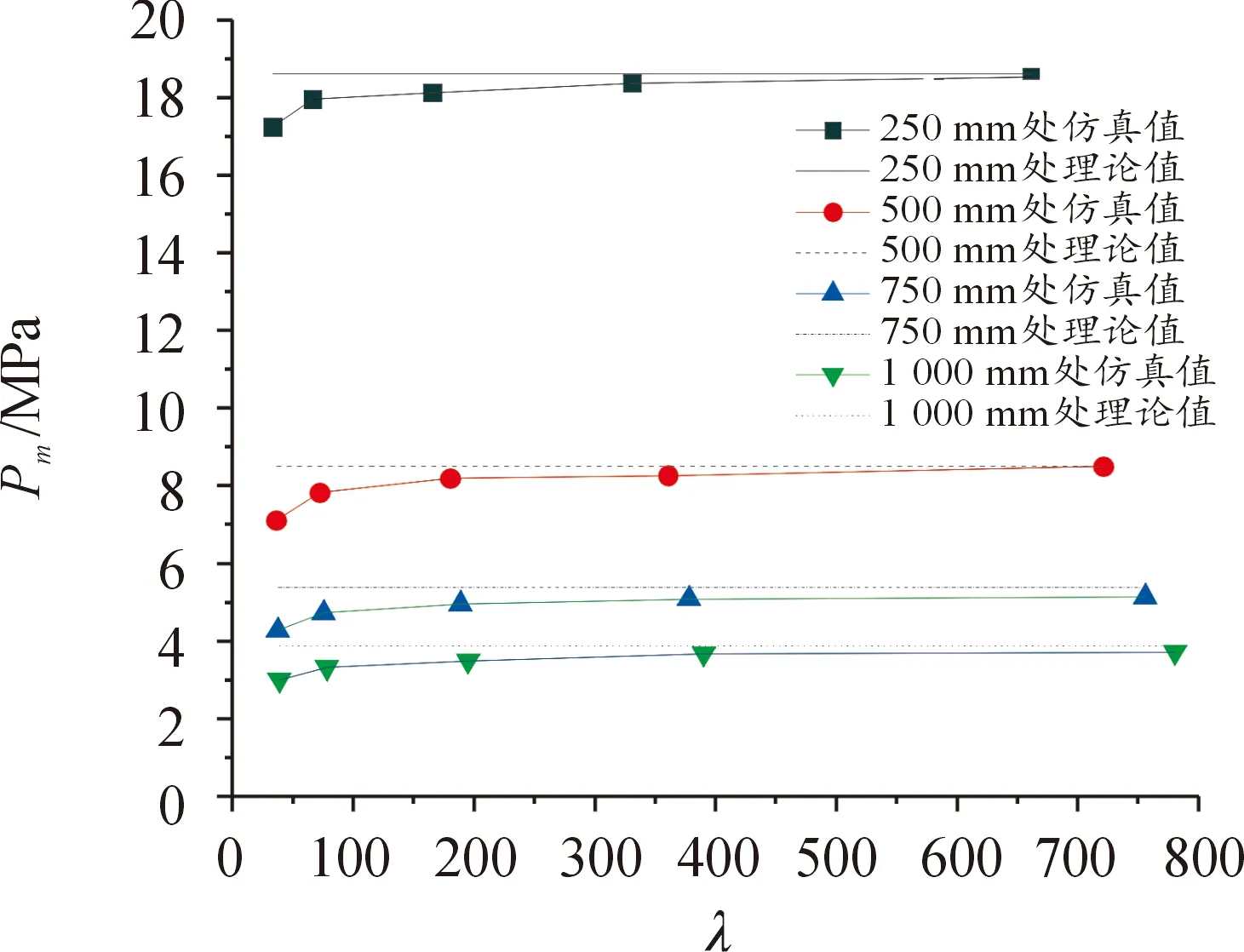
图5 不同比例距离下的冲击波压力峰值
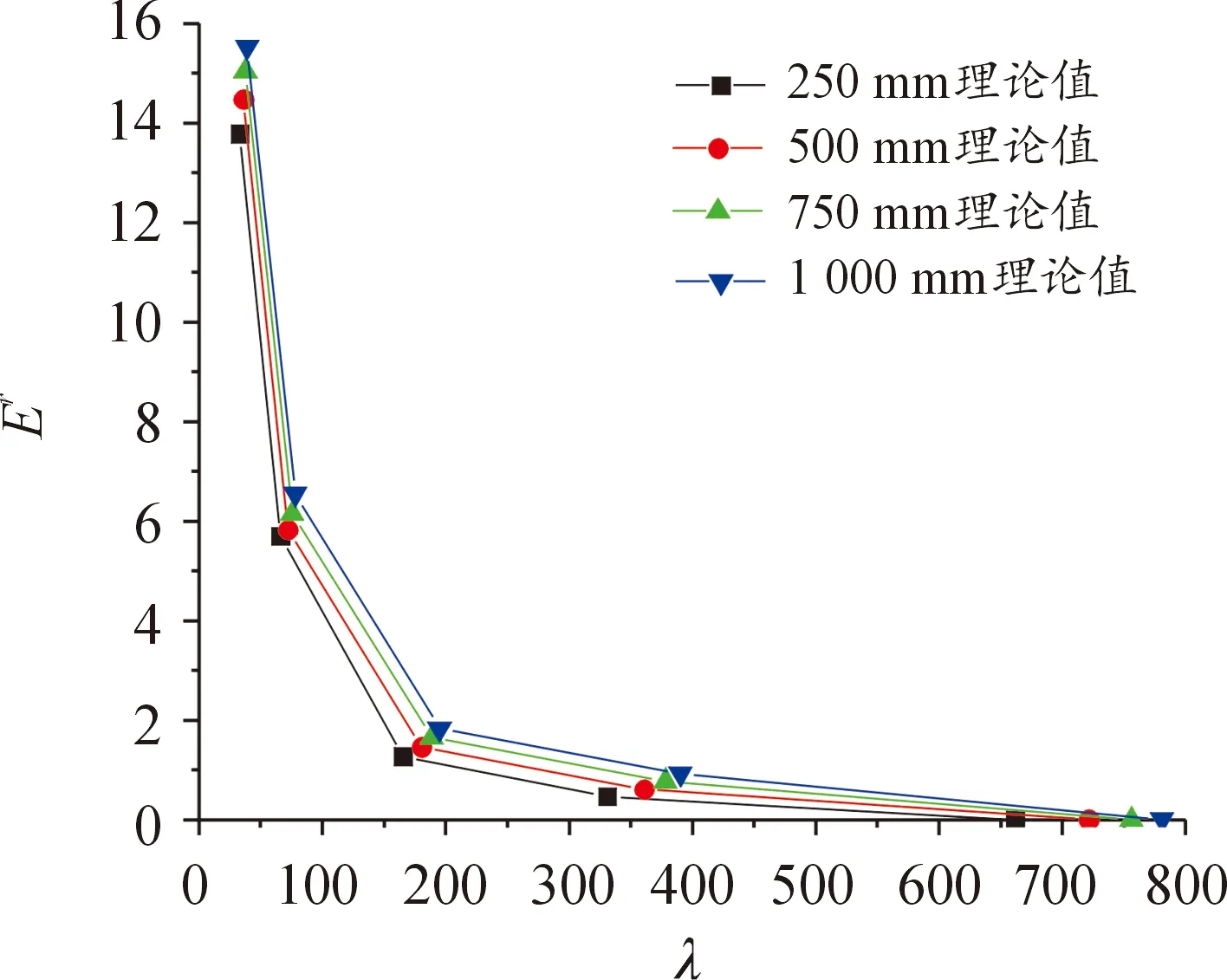
图6 各比例距离与最小网格尺寸下冲击波压力峰值的相对误差曲线
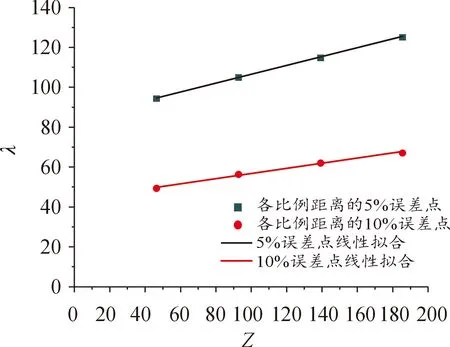
图7 5%及10%误差时网格尺寸与比例距离的关系

图8 不同药量下的冲击波压力峰值
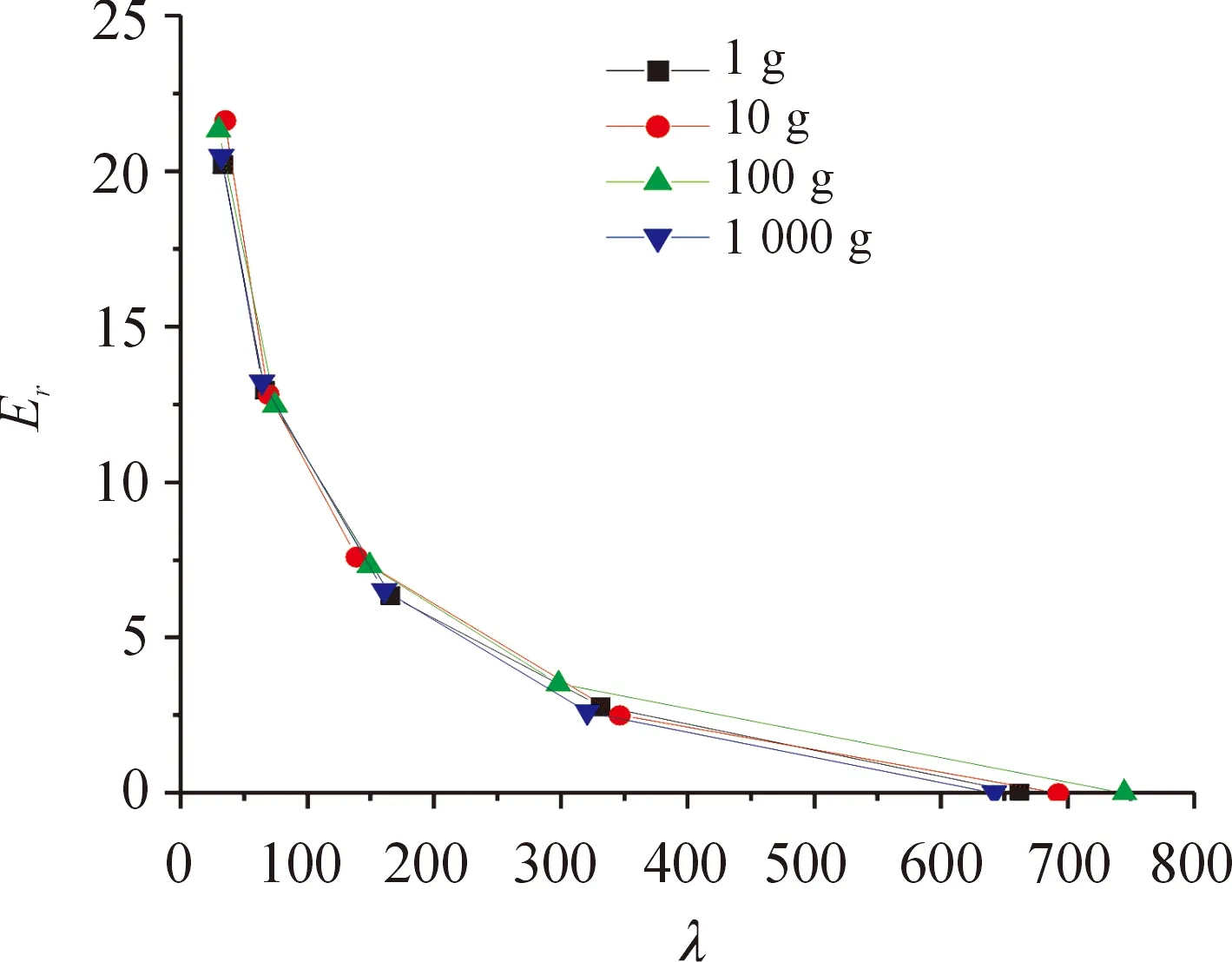
图9 各比例距离与最小网格尺寸下冲击波压力峰值的相对误差曲线

图10 5%及10%误差时网格尺寸与炸药药量的关系
5%误差时:λ=141.7+38.462Z
10%误差时:λ=83.6+17.486Z
4 试验验证
对得到的计算公式与试验结果进行对比,钟帅[28]在加压水罐中测过1.07 g当量炸药在0.388 m远处的冲击波压力峰值,水深为0.605 m时,测试冲击波压力为11.796 MPa。根据本文中得到的计算公式,设置的网格尺寸如表4所示。

表4 5%及10%误差下的网格尺寸
根据计算得到的网格尺寸建立仿真模型,仿真得到的结果如表5所示。仿真结果与实验测得数据相符,验证了网格尺寸最小取值公式的准确性。

表5 仿真结果与实验数据的对比
5 结论
本文中运用AUTODYN数值模拟软件,对水下爆炸仿真计算方法进行研究,并与试验结果进行对比,主要结论如下:
1) 采用一维楔形网格进行水下爆炸计算时,边界条件的选择对冲击波特性基本无影响,但对气泡脉动特性的影响较大;flow-out和transmit边界条件都无法同时兼顾冲击波和气泡2个载荷的计算精度,应设置足够大的水域才能模拟无限水域环境。
2) 气泡脉动周期与气泡半径随水域尺寸的增大呈幂指数增长趋势,综合准确度与计算量,在本装药条件下水域尺寸宜选择1 200倍装药半径。
3) 选取一个冲击波波长内的网格数量作为网格密度的特征参量,研究得到了不同比例距离和不同药量时网格密度对计算精度的影响规律,给出了TNT装药水下爆炸在5%误差和10%误差下网格尺寸最小取值的计算公式,并经实验验证了其合理性。
