水下仿生扑翼机器人的发展现状综述

2023-09-02曹永辉黄桥高屈毅林

数字海洋与水下攻防 2023年4期

曹勇，曹永辉，黄桥高，屈毅林，潘光

（1.西北工业大学航海学院，陕西西安 710072；2.西北工业大学宁波研究院无人航行技术研究中心，浙江宁波 315048）

1 扑翼式鱼类的生物学研究

1.1 生物原型分析

海洋覆盖着地球表面的71%，据不完全统计，海洋中的鱼类超过1.2万种。LINDSEY[1]根据不同推进部位将鱼类推进模式分为2大类：身体或尾鳍推进（Body and/or Caudal Fin propulsion，BCF）、中央鳍或对鳍推进（Media and/or Paired Fin propulsion，MPF）。根据已有的生物学信息可知：自然界中85%的鱼类以BCF模式游动。基于BCF模式游动具有快速性、高效性，同时，存在着稳定性不佳、低速时效率较低等缺点。基于MPF模式游动的鱼类由成对的胸鳍、背鳍、臀鳍的拍动或波动产生推力。近年来，基于MPF模式游动的鱼类以其优异的机动性和稳定性逐渐受到科研工作者的关注。

蝠鲼，又被称为魔鬼鱼，是一种典型的基于MPF模式游动的鱼类，属于脊索动物门、软骨鱼纲、燕魟目、蝠鲼科、蝠鲼属；其头侧有一对向前突出的由胸鳍分化的头鳍，胸鳍呈翼状，尾细且具尾刺。蝠鲼的身体部分扁平，呈菱形，具有一对尺寸较大而且运动较为灵活的近三角形的胸鳍[2]。蝠鲼在运动过程中，胸鳍基部变形较小，而胸鳍远端因为不受身体的约束，会产生较大的变形，这种柔性变形是其推力产生的主要来源。蝠鲼的运动效率较大程度上依赖于胸鳍的柔性变形[3]。蝠鲼在游动时，仅需拍动胸鳍即可实现矢量推进的效果，蝠鲼拥有如此高超的巡游能力离不开其独特的运动系统[4-11]。蝠鲼除了具有高效的巡游能力之外，还具有较高的机动性，其具体表现为：低速巡游过程中的快速转弯、高速巡游过程中的悬停以及悬停过程中的原地翻转等[12]。

KLAUSEWITZ等[2]通过对蝠鲼整体构造的研究与分析，得到了蝠鲼整体的外形比例等参数。将蝠鲼的最大展长定义为L，鱼体部分的展长为0.3L，单侧胸鳍的最大展长为0.35L。蝠鲼的俯视图近似于菱形，胸鳍左右对称，后缘端部有一凸起的垂直尾鳍，尾鳍后有数倍于体长的拖尾。在不考虑拖尾情况下，展长约为体长的2倍。最大展长方向与弦长方向交点处距蝠鲼头部距离为0.3L，距蝠鲼尾部距离为0.2L。KLAUSEWITZ将蝠鲼的胸鳍结构沿展向分为3部分，与身体相邻的1/3胸鳍结构称为基行（Basal row），靠近鳍尖的1/3胸鳍结构称为远行（Distal row）。

图1中给出了蝠鲼游动时向下和向上拍打的完整过程[2]，由此可以进一步看出蝠鲼胸鳍具有较好的柔性，在运动过程中会产生复杂的变形。

图1 蝠鲼运动说明Fig.1 Illustration of manta ray locomotion

1.2 生物结构研究

1973年，WEBB等[13]根据胸鳍所产生的无量纲波数W=BL/λ（其中BL代表体长，λ代表胸鳍弦向的行波波长）对鱼类的游动模态进行了划分：行波数大于1为波动模态、行波数小于0.5为摆动模态。1992年，HEINE等[14-15]测量并研究了真实牛鼻鲼运动时的姿态数据。通过分析其运动模态，HEINE发现：由于牛鼻鲼宽大的柔性胸鳍与身体完全相连接，使得胸鳍难以做出前后旋转的动作，因此需要通过胸鳍的主动变形与鳍在流场中的被动变形来适应不同的游动场景。1994年，GIBB等[16]通过解剖的方式研究了胸鳍的膜以及胸鳍内部骨架的弹性，并指出了胸鳍以及鱼体与流场相互作用的复杂性，同时说明了胸鳍的运动可以分解为：绕平行于身体轴线旋转的升沉运动及绕展向轴线旋转的俯仰运动。1996年，ARREOLA等[17]分析了条纹毛刺鱼的游动行为。发现在鱼的游动过程中，胸鳍总是异相拍动。2000年，ROSENBERGER[18]指出蝠鲼肌肉动作的基本单元是其肌肉细胞。其肌肉细胞在受到来自神经系统发出的刺激信号后，会立即作出应激收缩反应，缩短并变粗，在收缩反应后，肌肉细胞又快速恢复原状。蝠鲼胸鳍的肌肉与其桡骨之间存在联结，在其受到神经系统的刺激后，肌肉的收缩反应会带动相邻桡骨的运动，进而带动胸鳍鳍条产生变形运动。2001年，ROSENBERGER[19]对外形与鳐鱼类似的多种鱼类的推进模式进行研究，并发现：包括黄貂鱼在内的大多数都严格基于胸鳍运动，少数鱼类如锯鳐等严格地基于身体轴向摆动运动，另外，也存在像吉他鱼等在运动中将2种方式相结合。2005年，SCHAEFER等[5]通过研究典型MPF模式鱼类的肌肉类型、胸鳍骨架，发现胸鳍推进模式鱼类的胸鳍骨架有一定相似性，鳍骨沿展向呈放射状，沿弦向依次排列，靠近头部和翼根的部分钙化严重，刚性更强；鳍骨之间通过联结产生交叉支撑（cross-bracing），在形成支撑的同时便于胸鳍进行灵活变形以及波动传递，如图2所示[5]。2011年，CURET等[20]研究了蝠鲼胸鳍推进鱼类的外形、肌肉和骨骼分布，指出鳍条沿展向平行排列，每根鳍条在肌肉的作用下可绕着鳍根转动，且胸鳍具有交叉支撑结构。钙化的硬骨和软骨组成的放射性鳍条遍布蝠鲼胸鳍的内部，每根软骨鳍条由多段桡骨组成，可以绕关节小幅度转动，故在展向保持一定柔性。同时，相邻鳍条间依然存在交错式分布的联结，因此整个胸鳍面又表现出适度的刚性。2015年，RUSSO等[21]通过对胸鳍骨骼结缔组织的拉伸测试研究了牛鼻鲼和大西洋鳐胸鳍的柔性分布，同时提出了一种生物力学模型。该模型可以复现自然界中观察到的蝙蝠状骨骼结构的运动特性，还研究了骨骼结构变化对胸鳍变形特性的影响。2018年，SALAZAR等[22]通过对比黄貂鱼和蝠鲼的骨骼结构（如图3所示[22]），发现黄貂鱼胸鳍骨骼结构中的网状支撑部分更靠近身体内侧，扑翼边缘的骨骼较为独立分明；而蝠鲼的骨骼几乎都是交叉支撑结构。这种差异决定了黄貂鱼扑翼边缘可以更为自由的波动，而蝠鲼的运动则以整个扑翼的扑动或滑翔为主。

图2 基于MPF模式游动的鱼类骨骼分布[5]Fig.2 Distribution of fish bones based on MPF mode[5]

图3 黄貂鱼和蝠鲼的骨骼结构[22]Fig.3 Skeletal structure of stingrays and manta rays[22]

基于MPF模式游动的鱼类借助胸鳍和背鳍的拍动产生向前的推力，可实现6个自由度的运动、原地悬停、转弯等。其生物学的研究成果对于水下仿生扑翼机器人的设计具有重要意义。

生物学研究的主要手段为生物的活体观测，虽然生物的活体研究测量难度较高，产生的测量误差较大，但活体观测是建立生物体外形参数以及运动模型的基础。并且可以通过对活体进行运动学和涡结构的测量来讨论生物体的运动机理，以此指导仿生扑翼机器人的设计。

国内外研究团队进行了许多机理性研究以及水下仿生扑翼机器人的研制工作。但是在计算方法、控制机构设计、机械结构设计等方面依然存在着一些亟需解决的问题。水下仿生扑翼机器人的研究还停留在模仿其生物学特性研究方面。目前，已经研制的水下仿生扑翼机器人大多是从形态上接近真实生物，而其运动特性、感知特性、驱动特性的研究还处于起始阶段。

2 扑翼式鱼类的动力学研究

深入理解生物游动特性有助于更好地进行仿生机器人结构优化、建立基于模型的控制策略等，对于提升机器人运动性能、实现高精度姿态控制有着至关重要的意义。针对特殊问题的理论建模分析以及具有一般性的计算流体动力学（Computational Fluid Dynamics，CFD）是研究生物游动时流场特性的常用方法[23]。

2.1 动力学模型

起初，学者们对具有“细长体”特征的鱼类进行了研究并以此为基础发展了波动推进的动力学模型，此类模型适用于无量纲波数大于0.5的波动推进鱼类。LIGHTHILL[24-27]于20世纪60–70年代提出了大幅度可拉伸细长体理论（Large-Amplitude Elongated-Body Theory，LAEBT）。细长体理论将鱼体简化为由头部至尾部的一维杆件，杆长方向记为x轴。沿x轴上某一点垂直切分得到鱼体的截面Sx，位移h垂直于x轴。细长体理论假设固体周围的流动主要由2部分组成：可拉伸细长体周围沿游动方向的定常流动、由于细长体上某一点运动导致的非定常流动。若细长体以恒定速度U在不可压缩流体中向前游动，则欧拉观点下细长体周围某一处流体质点的速度[24]为

因此截面Sx处的流体所具有的动量为ρA(x)V(x,t）。进一步地，流体质点与鱼体此点之间的作用力可以通过动量的变化率[24]表示，即

将细长体上力做的功沿着弦向积分，并代入细长体的几何假设，可以得到细长体在变形时力所做功的平均值[24]为

在不考虑能量耗散时，细长体在单位时间内对于流体做功的能量主要由2部分组成：一是保持推进速度所需要的做功，二是施加到细长体周围流体质点的动能[24]，即

细长体单个周期产生的推力均值[24]为

式中，h(x,t)的形式对于推力均值的结果有重要的影响。因此，利用该理论进行分析时，需假定鱼体或机器人运动时符合某一变形规律。

考虑佛劳德推进效率[24]：

若细长体变形规律为h(x,t) =H(x)cos(ωt)，可得到推进效率最大值不超过1/2；若考虑细长体运动时有一行波经过，即

式中，c为行波的波速，可得到推进效率为

易知细长体上行波的传播速度与游速之比决定了推进效率。细长体理论在鱼体或机器人变形已知的情况下可以给出力和效率的计算方法，使得快速求解细长体动力学问题成为可能，但LAEBT方法忽视了固体自身的变形以及流体与固体之间的耦合作用[28]。

在一维细长体理论基础之上，WU等[29-31]发展了二维波动板理论。二维波动板将鱼体或机器人视为没有厚度的二维平面，仿生肌肉的运动变形看作平面上的行波，其维度增加至二维h（x，y，t），z为处于xoy平面上波动板垂直于平面的位移，WU讨论了在这种几何模型和运动形式下的动力学问题。CHOPRA等[32-35]通过结合Lighthill模型、机翼的有限纵横比理论（Finite Aspect Ratio Theory）以及涡流板理论（Vortex Panel Method），将模型的应用场景提升至二维、三维，并用于新模型计算了矩形板、三角形板以及新月形鱼尾的动力学问题。通过数值计算得出，当展弦比减小时，波动板产生的水动力及水动力效率将随之减小。在CANDELIER[36-38]提供的计算案例中，将该模型与CFD计算结果进行了对比，发现两者相差不超过10%。同时，通过将模型的计算结果与真实生物的水动力特性进行对比，发现相差不超过16%，进而证明了该模型的有效性。

另外，Cosserat杆作为软体机器人领域常用的模型之一，考虑了结构的被动变形、几何非线性等问题[39-41]。考虑流体作用时的LAEBT-Cosserat方法相较传统CFD方法，计算效率得到了显著的提升。

针对具有硬质骨骼的水下机器人扑翼的动力学建模问题，学者们一般采用基于莫里森方程的建模思路，其中基于叶素理论（Blade Element Theory）[42]推导基于MPF模式推进的仿生鱼动力学模型的方法应用较为广泛。叶素理论发展自刚性结构物旋转场景下的动力学建模问题，如螺旋桨、机翼、飞翼机器人[43-44]等，该理论是将结构视为若干微元的组合，先通过莫里森方程求解微元体的局部力学特性，再采用积分方法求解整个结构的受力情况。

针对机器人在水下借助扑翼进行推进的问题，考虑二维胸鳍由展向或者弦向的若干微元体组成，在机器人运动过程中，将微元体视为刚体。根据莫里森方程[44]，微元体上的受力可以表示为

式中：C为水动力参数；V为微元体表面上流体质点的合速度。对微元体的受力进行积分，可以得到整个扑翼的受力情况。根据机器人的几何特性，可以将积分方向分为垂直于流场方向、平行于流场方向、平行于仿生鳍前缘骨骼方向和垂直于仿生鳍前缘骨骼方向。

以平行于流场方向为例，考虑胸鳍展长为L的仿牛鼻鲼机器鱼以速度U向前游动。此时，与翼根处距离为r的微元体的有效攻角[45]为

式中：α（r）代表此处微元体周围流体质点合成速度与游动方向的夹角；β（r）代表此处微元体轴线方向与来流速度方向的夹角。

根据准稳态叶素理论，此时作用于微元体的升力、阻力[45]分别为

式中：ρ为流体密度；dS为微元体的面积；CLmax与CDmax为胸鳍的最大升力系数与最大阻力系数。对微元体受力沿着地面坐标系分解[45]可以得到

式中，φ为微元体与仿牛鼻鲼机器鱼机体纵平面的夹角。对微元体受力的3个分量在积分方向分别积分，可以获得胸鳍整体的受力表达式[45]

该建模方法的分析思路清晰，但将微元体视为刚体，未考虑运动过程中胸鳍的变形及流固耦合效应，且仅适用于无量纲波数较小（小于0.5）的摆动推进鱼类。

以莫里森方程为基础，通过修正模型中最大升力系数、阻力系数，可以求解不同摆动推进仿生结构的动力学问题。牛传猛等[45]基于叶素理论计算了仿牛鼻鲼机器人胸鳍的最大升力系数和最大阻力系数，并且通过给定展弦比和最大俯仰角，推算得到了升阻力系数公式。MENG等[46]基于莫里森方程研究了具有展弦向波动运动的六自由度仿生胸鳍结构的动力学问题，数值计算结果与水动力实验数据具有较高的一致性。WANG等[47-48]在稳准态叶素理论的基础上，结合攻角理论分析了仿生胸鳍的动力学问题，并将游动速度的数值模拟结果与机器人实际速度对比。结果表明，在攻角10°以内两者一致性较好。

根据无量纲波数的大小，可以将上述理论分为适用于波动推进模式（无量纲波数大于0.5）的细长体理论，以及适用于摆动推进模式（无量纲波数小于0.5）的叶素理论。通过结合不同的模型处理方法，基于这2种理论可以求解多种类型的水下推进动力学问题。但这2种理论的建模方法均需事先给定运动形式，且不考虑机器人与流体的流固耦合效应。

2.2 CFD水动力求解

随着计算流体力学学科的逐步发展和计算机技术的不断成熟，基于求解纳维–斯托克斯方程（Navier-Stokes Equations，N-S）的数值模拟方法被广泛应用。数值模拟方法可以获取随时间变化的流场细节，模拟鱼类游动的真实环境，有助于研究者们理解生物游动的机理。目前数值模拟方法面临的较大难点在于如何处理边界运动问题，运用传统贴体网格模拟生物游动时往往伴随着网格畸变，极大影响了计算的效率和结果的准确性。为解决网格大变形问题，研究者们提出了几种解决方法，如任意拉格朗日–欧拉（Arbitrary Lagrangian-Eulerian，ALE）方法、时空方法和浸没边界方法（Immersed Boundary Method，IBM）[49-51]。

ALE方法描述了运动参考系中的流场，最初是由HIRT等[52]在结构网格的有限差分框架中引入，SHASHKOV等[53-54]将具有有限差分框架的ALE方法推广到任意多边形网格中。在ALE方法中，网格伴随着流体和固体的交界面运动，因此网格速度是N-S方程对流项中的一个参数[55]。KERN等[56]利用ALE方法研究了鳗鱼型生物爆发性游动的流体动力学，得到了一些与实验观测结果一致的尾迹结构，定量分析了生物游动所受到的力，证明了波动型生物会根据不同的目标修改它们的运动形式；KATUMATA等[57]利用ALE法对波状斑马鱼游动时的涡旋结构进行了详细预测，评估了生物的水动力、功率和速度，证实涡环结构能够促进生物游动时水动力的产生。LI等[58]基于流体–结构相互作用（Fluid-Structure Interaction，FSI）方法，分析了金枪鱼类从静止状态到稳定巡航状态加速过程中的游动性能和机理，对自推进行为的流体动力学进行了系统的参数研究。

时空法基于时空有限元公式，该公式已成功应用于固定空间域中的各种可压缩和不可压缩流动问题，其中有限元插值多项式是空间和时间的函数[55]。TEZDUYAR等[59]提出了一种变形空间域/时空方法（Deforming-Spatial-Domain/Space-Time，DSD/ST），该方法通过一种时空/时间有限元的概念来处理计算域的变形，网格随着流体与固体的边界一起运动。随后该方法被陆夕云等[60]用于生物游动的数值计算中。

浸入边界法将流场中的实体看作是N-S方程中的一个动量强迫项，并非一个真实的实体。由于浸没边界法的网格运动通常不遵循浸没体的边界，因此选择满足浸没体上无滑移条件的精确插值方案至关重要[55]。这种方法最早由PESKIN[61]在1972年提出，并将其用于模拟心脏瓣膜的运动，后来被广泛应用在具有大变形的生物流场求解当中。传统的IBM方法采用一种数值虚构的方法模拟边界对流体分布力的作用，采用欧拉变量描述流场的物理量，拉格朗日变量描述边界运动产生的物理量，用Delta函数通过分布节点力和插值速度来表示流场和浸入边界的数值交互。由于浸没边界法的流场在正交的笛卡尔网格中进行计算，避免了贴体网格的生成，从而有效避免了网格畸变问题，非常适用于生物游动的流场计算。

但传统的IBM方法也存在很多缺点，如无滑移条件无法严格满足、速度穿透问题、边界不精确等。因此在随后的研究中，各种改进的IBM方法不断出现。MITTAL等[62]提出了一种精确边界的浸入边界方法来模拟复杂的三维变形问题，该方法基于离散力格式，采用鬼点策略来满足精确的速度和压力边界条件，通过对鱼的胸鳍运动以及蜻蜓飞行的模拟表明该方法具有较高的求解效率以及计算精度。DONG等[63]利用这种方法模拟了蓝鳃太阳鱼在稳定向前运动过程中的流场情况，定量表征了胸鳍的推进性能，详细分析了推力产生的机制，以及推力与涡旋动力学的联系。仿真结果表明，采用主动和被动鳍变形驱动是生物具有较高的推进性能的重要原因。HAN等[64]采用基于浸没边界法的不可压缩N-S流动求解器，在平稳的笛卡尔网格上模拟了背/臀鳍在中鳍相互作用（Median Fin Interactions，MFI）推进中的水动力影响。模拟中发现，由于后体涡旋（Posterior Body Vortices，PBVs）与尾鳍前缘涡旋（Leading Edge Vortices，LEVs）的碰撞，后者得到了增强，同时尾鳍的推力和效率也分别提高了25.6%和29.2%。研究表明增加背/臀鳍面积会导致更强的LEVs，改变背/臀鳍扑动的时间段会影响PBVs与LEVs的碰撞时间，从而改变尾鳍性能。

以上方法在求解不可压流动时会出现速度–压力的解耦，解耦产生的压力泊松方程一般采用迭代的方式进行计算，这使得数值计算收敛所消耗的资源较多。为解决这个问题，YANG等[65-66]将IBM与气体动理学格式（Gas Kinetic Scheme，GKS）结合，成功应用于不可压流体的求解，大大提高了N-S方程的求解效率。但该方法采用显式算法，在拉格朗日网格量较多时求解效率低下。ZHANG等[67]基于三维显式IB-SGKS通量求解器，针对牛鼻鲼前游动过程中胸鳍大变形问题进行计算方法的改进。通过探讨不同的线性方程组求解策略，以及对拉格朗日点周围欧拉点的搜索策略进行改进，从而解决原求解器在拉格朗日网格节点数大于1 000时计算效率低下的问题。研究结果发现在斯特劳哈尔数较高时，翼尖涡的脱落是推力产生的主要原因，而前缘涡和后缘涡的脱落则对推力产生不利的影响。但在斯特劳哈尔数较低时，前缘涡的脱落会对推力产生有利的影响。

目前流行的商业软件采用的主要是ALE方法，存在计算结果不准确、复杂运动较难实现等局限性；时空法无法对三维模型进行分析，并且在分析二维问题时消耗的计算资源较多；浸入边界法受制于流体和固体求解器的先进性，其计算结果的可行性仍然值得商榷。同时如何将生物的主动变形和被动变形相结合也是一大研究难点。

3 水下仿生扑翼机器人的驱动与样机研究

基于前文对MPF模式的定义，自然界中，牛鼻鲼、蝠鲼、鹰嘴鳐等的推进方式为摆动推进；黄貂鱼、尼罗河魔鬼、南美刀鱼等的推进方式为波动推进。相比于BCF模式，MPF模式具备更强的稳定性和机动性。随着仿生机器鱼领域研究的不断深入，MPF模式逐渐成为仿生机器鱼领域的研究热点。国内外很多研究机构根据MPF模式的运动特点陆续开发出多款仿生机器鱼。

3.1 摆动推进的仿生胸鳍结构

2008年，德国FESTO公司、EvoLogics公司与柏林科技大学3家单位合作开发了一款名为Aqua Ray的仿蝠鲼机器鱼，如图4所示[68]。该机器鱼采用无刷电机驱动的水泵为2对液压装置提供动力，并通过线绳驱动胸鳍骨架上下扑动。该机器鱼还在胸鳍结构中采用了Fin Ray结构，可以使仿生胸鳍的运动形态与真实生物更加贴合。利用位于鳍尖的单台舵机使胸鳍产生弦向扭转变形，从而产生推进力。同时，利用尾鳍实现上浮下潜运动。该机器鱼可以实现以0.5 m/s的速度进行游动。2010年，ZHOU等人开发了一款名为RoMan-II的仿蝠鲼机器鱼。该机器鱼采用多个独立电机驱动，并列两侧的胸鳍由3根独立的柔性鳍条驱动，每根鳍条都有单独的驱动源提供动力，机器鱼的升沉运动采用类似鱼鳔的给排水装置进行控制，可实现最大0.3 m/s的水下巡游速度[2]。2016年，CHEW等人[69]研制了一款采用单鳍条驱动的仿生蝠鲼机器鱼。该机器鱼单侧胸鳍的展长为194 mm，最大弦长为200 mm，鳍条位于仿生胸鳍的最前端，鳍面其余部分为柔性橡胶材料。通过舵机驱动单鳍条使柔性鳍面变形进而为机器鱼提供推力。同时，研究人员还针对不同厚度柔性胸鳍的推进效果进行了实验研究，发现该机器鱼最快可以达到0.5 m/s的游动速度，约为体长的1.78倍[69]。

图4 Aqua Ray仿蝠鲼机器鱼[68]Fig.4 Manta ray-inspired robotic fish Aqua Ray[68]

北京航空航天大学机器人研究所的毕树生等人自2007年起，做了大量MPF模式的仿生鱼研究，研制了五代样机（Robo Ray系列），其中，游动速度最快可以达到0.9 m/s。样机多采用多电机带动多鳍条的胸鳍结构形式，在运动形态和整体结构上，仿生机器人与自然界中真实蝠鲼的相似度已逐渐提高[70-78]。2011年，国防科技大学杨少波等[79]从仿生学层面系统地开展了牛鼻鲼胸鳍推进模式的研究，研究团队基于流固耦合的方法分析了牛鼻鲼胸鳍推进时的水动力学特性，并研制了一款名为Cownose Ray的仿牛鼻鲼机器鱼，如图5所示。团队通过样机的航行实验研究了不同的运动参数下潜水器的推进性能，该机器鱼可以在1 Hz的扑动频率下以0.18 m/s的速度游动[79-81]。2022年，中国科学院的喻俊志等[46，82]研制了一款后掠角可变的MPF仿蝠鲼机器鱼。该机器鱼展长723 mm，最大弦长381 mm，最大可以实现每秒1.07倍体长的游动速度，基于后掠角可变的胸鳍结构，该机器鱼的机动性得到了大幅的提升，可实现快速的俯仰机动，其半径为205 mm。同时，研究团队针对该样机提出了基于准稳态方法的动力学模型。同年，洛桑联邦理工的SUN等[83]通过多个齿轮泵构建了柔性致动器，可产生最大约25 N·m的力矩，并在此基础上开发了一款胸鳍推进的仿生机器鱼。该样机展长1.93 m，其扑动频率达到了0.5 Hz，游动速度约0.29 m/s。该机器鱼的驱动方式为设计工程实际中所需求的大尺度软体机器人提供了新的研究思路。西北工业大学的曹勇等[84-89]采用单舵机驱动单根鳍条、多台舵机驱动并联多根鳍条、双驱动带动多连杆等结构方式开发了多台仿蝠鲼机器鱼，如图6所示[84]。其研发的翼身融合水下滑翔工程样机完成了多次湖、海试验工作，并实现了最大1 025 m的下潜深度，是目前国内外唯一具备大深度水下工作能力的仿生潜水器。

图5 Cownose Ray仿牛鼻鲼机器鱼[79]Fig.5 Cownose ray-inspired robotic fish Cownose Ray[79]

图6 西北工业大学仿蝠鲼机器鱼[84]Fig.6 Manta ray-inspired robotic fish from Northwestern Polytechnical University[84]

根据以上列举的研究成果，可以发现，摆动推进的仿生机器鱼在航行性能以及与生物的相似程度在逐步提升，同时也逐渐从实验室研究阶段走向工程应用阶段，具备较好的应用前景。摆动推进的仿生机器鱼展弦比通常处于1～2之间，因此两侧胸鳍在存在推力差时，对于转弯机动性有较为明显的提升，尤其是在机器鱼处于低速巡游情况下。但摆动推进的机器鱼存在纵向稳定性差的问题，这主要是因为胸鳍扑动过程中产生的水动力是周期性变化的，这也对胸鳍驱动结构设计以及运动控制提出了新的挑战。

3.2 波动推进的仿生胸鳍结构

HU等[90]参照“尼罗河魔鬼”（Gymnarchus Niloticus）的长条状背鳍，开发了一款名为RoboGnilos的波动仿生鳍装置。该样机由并列排布的9台舵机驱动，每台舵机带动独立鳍条，鳍条间通过柔性薄膜进行连接，通过调节舵机之间的相位差可以实现柔性薄膜波动波长的调节，该装置可以达到约0.35 m/s的游动速度。CURET等[91]参照南美刀鱼的腹鳍，开发了一款名为Robotic Knifefish的仿生波动鳍装置。该装置由并列排布的32台舵机驱动，由于该装置驱动数目的增加，在运动过程中胸鳍可以产生连续性更好的行波。CURET利用DPIV方法，对装置的波动传递方式差异引起的涡结构、推力以及侧向力变化进行了分析。结果表明，该装置产生的最大射流速度可达0.5 m/s、最大升力可达0.4 N。

LIU等[92]同样参照南美刀鱼的腹鳍，开发了一款可自主游动的仿生波动鳍机器鱼，如图7所示。该机器鱼采用单驱动形式，在波动鳍前缘，由一台连续转动的电机驱动曲柄摇杆机构往复运动，并带动柔性鳍面运动。由于该机器鱼仅在前缘进行驱动，鳍面的波动呈现由前缘至后缘振幅逐渐衰减的趋势。相较于多驱动结构的波动鳍装置，单驱动结构由于完全依赖鳍面的被动变形，因此不会产生额外的运动消耗，在推进能耗上有大幅下降，但逐渐衰减的波动振幅也限制了机器鱼推进能力的进一步提升。经测试，该机器鱼可达到约0.25 m/s的游动速度[92]。LIU等人开发了一款名为KnifeBot的仿生波动鳍机器鱼，该机器鱼可实现最大约0.35 m/s的游动速度。该机器鱼由并列排布的16台舵机驱动，通过调节舵机相位差调节鳍面波长以及波动传递方向，其利用DPIV方法对该机器鱼的不同波动传递方式进行了研究，得益于该机器鱼的自主游动能力，除游动速度外，还可获得不同波长、扑动频率对俯仰角、横滚角、偏航角的影响规律[93]。

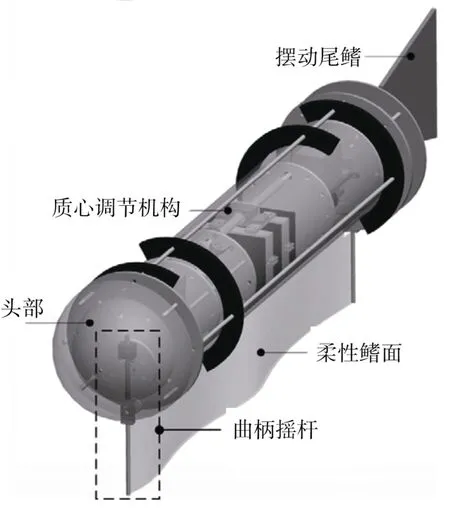
图7 仿刀鱼波动鳍机器鱼[92]Fig.7 Knifefish-inspired robotic fish with fluctuating fin[92]

国防科技大学与Pliant Energy Systems公司分别开发了2款可实现水陆两栖的仿生波动鳍机器人，如图8所示[94]。二者分别采用橡胶以及硅胶作为鳍面材料，其中，由于前者鳍面材料硬度更高，使得其可在水下、沙地、冰面以及雪地等多种地形条件下实现快速运动，后者爬行速度约为0.1 m/s，游动速度为0.3 m/s[94-95]。

图8 水陆两栖仿生波动鳍机器鱼[94]Fig.8 Amphibious bionic robot fish with fluctuating fin[94]

根据以上列举的研究成果，可以发现，波动推进的仿生鱼逐渐脱离了仿生对象的束缚，从单波动鳍过渡到多波动鳍，并利用波动传递的特性，使波动鳍机器鱼具备了水–陆两栖的功能，具备较好的应用前景。波动推进的仿生机器鱼展弦比通常处于小于1，且鳍面存在的无量纲波数大于1，这就使得其产生的推力是连续的，因此也具备更好的稳定性。但波动推进机器鱼由于采用多个驱动装置，且驱动装置之间通过柔性材料连接，在运动过程中会存在运动和变形相互制约，相互影响的情况，因此功耗较高，对能源系统提出了新的挑战。

3.3 采用软体驱动器的胸鳍推进机器鱼

软体驱动器是指全部或部分由柔性材料制成、能够实现连续变形的驱动器，相比于传统刚性驱动器，其具备极高的运动自由度和极强的环境适应性，还可实现自组装、自修复、自感知等功能，在胸鳍推进的仿生机器鱼领域有巨大的应用空间。

已经研制的胸鳍推进式软体机器鱼所采用的驱动方式包括：气动[72，96-97]、形状记忆合金（Shape Memory Alloy，SMA）[98-100]、离子聚合物–金属复合材料（Ionic Polymer-metal Composites，IPMC）[101-103]、介电弹性体驱动（Dielectric Elastomer Actuator，DEA）[104-105]和生物融合驱动（Bio-hybrid Actuation）[10，106]。

气动指在软体结构中充入气体，通过改变气体体积或内部压力，使结构产生运动与变形的一种驱动方式。日本冈山大学SUZUMORI等[96]及北京航空航天大学CAI等[72]都先后研制了胸鳍推进的气动软体机器鱼。2022年，CHI等采用气动驱动并结合多稳态结构成功研制了胸鳍推进的蝶泳式机器鱼，游动速度可达每秒3.74倍体长，是目前世界上游动最快的软体机器鱼[97]。气动具有驱动力强、运动灵活等优势；其发展较早且十分成熟，但通常需要外接气源，因此不适用于无缆的自主游动。

基于SMA材料驱动器的基本原理是：通过电流、光照等方式加热使SMA产生相变，同时产生变形。KIM等[98]研发了一种基于SMA驱动的仿生海龟。WANG等[99]设计研究了一种基于SMA驱动的摆尾机器鱼和仿蝠鲼机器鱼。基于SMA的驱动器具有驱动力大、变形量大等优势；但由于其散热较慢，驱动后较长时间才能够恢复至初始状态，导致驱动频率较低。

IPMC是一种电活性聚合物材料（Electroactive Polymer，EAP）。在IPMC的电极两端施加电压时，水合阳离子在电场作用下移向负极，负极产生拉伸变形，同时，正极发生收缩变形，材料整体则发生弯曲变形。HUBBARD等[101]将IPMC应用于仿生机器鱼胸鳍和尾鳍的驱动设计。SHEN等[102]通过模仿海豚的游动方式，使用IPMC研发了一款仿生机器鱼，并研究了其水动力性能。弗吉尼亚大学的研究者[103]基于IPMC驱动研发了一款仿生蝠鲼机器鱼，该机器鱼的胸鳍由两侧的IPMC鳍条驱动，身长80 mm，翼展180 mm，最大游动速度为4.2 mm/s。IPMC具有变形灵活、位移大、驱动电压低、响应速度快等优点。由于其驱动需要液体环境，因此IPMC与机器鱼适配性强。但IPMC仍存在输出力度小、响应频率低等不足，在实现复杂运动和高效控制方面仍面临一些挑战。

以介电弹性体薄膜结构为例，可以对DEA的驱动原理进行简单说明：在介电弹性体薄膜上下两侧的电极上施加电压，介电弹性体薄膜在Maxwell应力的作用下发生变形，例如薄膜厚度减小，横向产生扩张等。近期，LI等[104]研制了介电弹性体驱动的仿生狮子鱼，完成了马里亚纳海沟的深海驱动实验，并实现了全局视觉下软体机器鱼集群运动实验[105]。介电弹性体驱动器具有极高的能量密度和良好的频率响应特性，在许多领域都有着广阔的应用前景。但由于其机理复杂，在设计仿生运动时仍有很大挑战。

生物融合驱动指：将生物材料如动物肌肉组织作为驱动器整合到软体机器人系统中，使其针对外界刺激（如电场、光刺激等）做出反应的一种驱动方式。2016年，PARK等[10]利用大鼠心肌细胞研制了一种生物融合驱动的黄貂鱼机器人，所研制的机器人能够通过光趋近进行导航。2022年，ZHANG等[106]成功研制了一种肌肉组织驱动的仿蝠鲼机器人，其仅由一块肌肉组织驱动就可以实现有效推进。生物融合驱动的生物兼容性强，能对外界刺激（光信号、电场等）做出反应，但其制备困难，对环境要求高，该领域的研究目前仍处于起始阶段。

除此之外，软体驱动还包括燃烧（化学驱动）、电液压驱动（Electrohydraulic Actuation）等驱动方式。其中，燃烧能够在短时间内爆发大量能量，但二次驱动效果差，在弹跳机器人[107]、跨介质机器人[108]领域应用广泛。针对软体机器鱼的设计而言，不难看出，化学驱动在快速逃逸、跃出水面等研究方向具备巨大潜力。2018年，ACOME等[109]提出的HASEL驱动器（Hydraulically Amplified Self-Healing Electrostatic Actuator，HASEL Actuator）是一类典型的电液压驱动器，能够实现拉伸[110]、弯曲[111]、旋转[112]、扭转[113]等多种运动及变形形式。其能量密度高、输出能力强、易于快速制备，在设计具备复杂仿生运动能力的胸鳍推进软体机器鱼方面具备广阔的前景。

根据以上所列举的研究成果，可以看出，大部分研究工作主要关注具体软体驱动机理，所研制的机器鱼样机运动形式单一、操控性差，难以实现复杂仿生运动。在扑翼软体机器鱼的研究过程中，还面临着许多挑战：例如，在驱动器层面，如何设计和研制能够满足胸鳍推进特性的软体驱动器；在系统层面，如何根据鱼类胸鳍运动变形特性，采用一种或多种软体驱动方式设计具备复杂仿生运动能力的仿生胸鳍推进系统；在运动控制层面，如何根据软体驱动器驱动特性设计运动控制系统，实现复杂仿生运动控制。总而言之，在运动效果和应用能力方面，与传统机器鱼相比，软体机器鱼仍有较大的提升空间。

4 水下仿生扑翼机器人的控制研究

本节根据水下扑翼机器人的控制目标，将水下扑翼机器人的控制研究内容分为以下几大类：1）扑翼驱动控制；2）俯仰与深度控制；3）转弯与航向控制；4）路径点与路径跟踪；5）避障与自主游动；6）基于相似度的运动参数优化。针对以上研究内容，本节主要阐述面向不同控制任务的控制要求与难点，讨论不同控制器对同一控制目标的应用特点，为水下扑翼机器人的控制器设计提供参考。

4.1 扑翼驱动控制

水下扑翼机器人的游动借助成对扑翼的拍动或波动，通过扑翼运动过程中与水的相互作用，推进自身游动。目前，扑翼驱动控制的方法要有基于运动学模型的方法、基于动力学模型的方法以及基于中央模式发生器（Central Pattern Generators，CPG）的方法等[114-118]。

针对基于运动学模型的方法，LOW等[119]利用模型的运动学方程，导出了2种形式的多链机器鱼步态规划的一般解，该解被用作六链体尾鳍式机器鱼、八链胸鳍式机器鱼游动试验的步态控制输入，实现了对RoMan-III两侧柔性胸鳍的驱动，实验表明其开环游动的最大速度为0.45 m/s。WU等[120]提出了一种基于连杆机构的新型仿蝠鲼机器人，作者对连杆机构的运动学模型进行了分析，并进行了仿生机器人的水下实验，其胸鳍的运动轨迹与蝠鲼胸鳍的运动轨迹相近。LIU等[121]对仿蝠鲼机器人进行了运动学和水动力学的仿真分析，并在水池中进行了测试，该机器人能通过改变两侧胸鳍的幅值实现简单的横滚和俯仰运动，从而实现游动和转向。WANG等[122]提出了一种基于波动式胸鳍的仿蝠鲼机器人，并对波动式胸鳍的运动学模型进行了分析，实现了前后游动、俯仰、转弯3个基本动作并进行了评价。

针对基于动力学模型的方法，CAI等[123]、MENG等[46]建立了仿生胸鳍的简化水动力学模型，测试了所设计的胸鳍机构及仿蝠鲼机器人的运动性能，但仿真结果与实验结果之间仍有明显的误差。目前，由于刚体与柔性耦合变形的水动力分析十分复杂，建立一个精确的胸鳍动力学模型是非常困难的。因此，基于动力学模型的驱动控制方法仍然较少。

基于目前的情况，更加稳定、可靠且无需节奏信号反馈的CPG方法开始被大量运用。CAI等[124-125]开展了仿蝠鲼机器鱼的CPG多运动模态协调控制研究，进行胸尾鳍结构的驱动，实现了扑动前游、倒游、原地转弯等运动姿态；ZHANG等[126]设计了一个CPG模型，实现了仿生机器鱼的多模态机动运动，实验表明利用胸尾鳍一体化推进机构，机器鱼可以更稳定、更高效地进行灵活的机动游动；CAO等[123]改进了基于相位振荡器的CPG模型，引入了空间与时间上的非对称效应，完成了对多鳍条胸鳍结构的驱动，并进行实验测试了其运动性能。

4.2 俯仰与深度控制

上浮与下潜2种运动状态是水下扑翼机器人完成深度控制的基础。水下扑翼机器人机械机构设计的差异会导致其实现2种运动的方式不同[89]。例如，只拥有浮力系统的机器人可以在速度为零的情况下实现运动深度的改变，而只拥有重心调节机构的机器人则需要在机器人具备一定前游速度的基础上，通过调节重心位置改变俯仰力矩，进而改变俯仰角，最后实现运动深度的调节。同时，拥有可上下偏转的尾鳍的机器人也可以在具备一定的前游速度的基础下通过调节尾鳍的偏置角度改变运动的深度[127]。当尾鳍向上偏置时，尾部受到的力会使得机器人产生抬头力矩，机器人呈现上浮运动状态，进而运动深度变小；当尾鳍向下偏置时，尾部受到的力会使得机器人产生低头力矩，机器人呈现下潜运动状态，进而运动深度变大。

由于尾鳍具有不占用额外的舱内空间、且结构设计相对简单的优点，因此在进行水下扑翼机器人设计时，小尺寸样机通常只包含尾鳍机构[127]，而大尺寸样机通常同时包含重心调节机构与浮力系统[89]。

针对水下扑翼机器人深度控制，研究人员以尽量快速的按照平滑轨迹到达某一固定深度，并保持在这一深度游动为目标开展了相关研究。NIU等[127]通过调节尾鳍的偏转角度，采用基于模糊逻辑的方法实现了机器人的深度控制，并通过实验验证了基于模糊逻辑的深度控制方法的有效性；WANG等[122]通过实验研究了“RobCutt-I”的运动速度与波形传动的运动学参数之间的关系，包括向前/向后游泳、潜水/上升和转弯3个运动状态，在此基础上提出了将自抗扰控制（Active Disturbance Rejection Control，ADRC）与模糊策略相结合的混合控制，以实现深度和航向的闭环控制；德国EvoLogics GmbH公司与吕贝克应用科学大学[128]研制的Manta Ray AUV包括2个喷气发动机、4个垂直推进器、2个机翼伺服系统、2个扭转机翼伺服系统和1个尾部伺服系统，这种配置使得它具备动态深度控制能力，可以实现高精度的深度保持控制，同时具备迅速完成潜水或爬升动作的能力；CAO等[129]设计了一种仿牛鼻鲼机器人Robo-ray，通过2个尾鳍来实现该机器人的控制深度，基于CPG-模糊算法提出了开环速度控制、闭环深度控制和航向控制方法。闭环实验结果表明，机器人的深度控制误差小于6.1 cm，航向控制误差小于6°；XIE等[86]考虑到未知的动力学和外部环境干扰，设计了一个基于CPG的经典高木–关野（Takagi- Sugeno，T-S）模糊神经网络控制器用于仿蝠鲼机器人的航向和深度控制，并通过水池测试验证了控制器的有效性，其深度跟踪和航向跟踪控制误差分别为±6 cm和±6°；HE等[130]为了提高仿蝠鲼机器人的深度跟踪能力，考虑仿蝠鲼机器人的纵向运动特性，设计了一个基于非对称输出S平面的深度控制器。最后，通过水池实验验证了仿蝠鲼机器人深度控制器的可行性和可靠性。实验结果表明，深度控制误差在±5 cm以内。

4.3 转弯与航向控制

水下扑翼机器人的扑翼在扑动过程中的波动，可以简单地分解为弦向的波动和展向的波动。水下扑翼机器人主要通过3种方式进行转弯：两侧非对称振幅方式和两侧鳍条间非对称弦向相位差方式，以及非对称振幅和非对称相位差结合的方式[118，129]。

基于非对称振幅的转弯方式，一侧扑翼的扑动振幅大于另一侧，扑动振幅较大的一侧产生更大的推进力，导致两侧扑翼的推进力不同，形成转弯力矩[123]，从而使机器人转向振幅小的或无拍动振幅的一侧，实现航向的调整。基于非对称振幅的转弯模式具有较慢的转弯角速度和较大的转弯半径，因此该方法适用于小范围内的航向调整。

基于非对称相位差的转弯方式，扑翼的波动传递方向或快慢不同，因此两侧扑翼的推进力大小不同，形成一个大的转弯力矩[123]。该转弯方式主要用于快速响应时的机动转向。因此，基于非对称相位差的转弯模式适用于转弯角速度快、转弯半径小的大航向调整。

航向控制的主要任务是通过调节两侧胸鳍非对称振幅及相位差，使机器人的实际航向趋近于期望航向。基于上述目标，WANG等[122，131]提出了一种ADRC与模糊控制策略相结合的混合控制方法来进行航向控制，该方法在实验样机RobCutt-I、RobCutt-II上进行了实验，设定航向从70°调整到210°，稳定时间约为12 s，且超调量较小。针对单一依靠非对称振幅及相位差进行航向调整存在的问题，HAO等[87]结合2种转弯方式的特点，利用非对称相位差快速调整航向，利用非对称振幅精确调整航向，实现了闭环航向控制。通过航向干扰实验，验证了2种转弯方式结合比单一方式更有效，并通过矩形轨迹游动实验验证了该机器人在2种转弯方式结合下的机动性。此外，非对称振幅可以提前改变预期的相位差，确保输出的平稳过渡，实现快速准确的调整。针对上述航向控制方法精度不高的问题，XIE等[86]提出了一种将CPG和基于T-S模糊神经网络（Neural Network，NN）的控制相结合的控制方案，该方法基于实验数据构建航向数据集，并使用相应的数据集完成对所建立的T-S模糊神经网络的训练，提出了基于CPG网络的航向控制器，其中参数由T-S神经网络获取，最后，实验结果表明该仿蝠鲼机器人的航向控制误差为±6°，航向控制精度有所提高，验证了该控制器的有效性和鲁棒性。HE等[130]以仿蝠鲼机器人在航向角变化较大的情况下实现良好的航向跟踪效果为目标，结合模糊控制器和航向过渡目标值函数，基于S平面控制方法设计了仿蝠鲼机器人的航向控制器，最后，通过水池实验验证了蝠鲼机器人航向控制器的可行性和可靠性。实验结果表明，航向控制误差在±5°以内，与经典S面航向控制器相比，改进S面航向控制器的超调量较小，且航向切换后的误差较小。

4.4 路径点与路径跟踪

根据不同的控制目标，跟踪问题可分为路径点跟踪和路径跟踪[132]。路径点跟踪的含义为机器人经过一系列给定的路径点游动，路径跟踪的含义为机器人按照制定的最优几何参考路径游动[133-135]。

在运用路径规划算法规划好一条从起点到目标点的最优路径后，机器人从起点出发，按照某种控制规律进行运动，到达该最优路径并实现对其的跟踪。如何让机器人跟踪该最优路径，是路径跟踪需解决的关键问题[136]。路径跟踪的实质是通过控制水下机器人的运动来减少机器人与参考轨迹之间的空间误差。若考虑轨迹跟踪，则需包含时间上的误差。然而，水下扑翼机器人的模型不确定性和来自波浪和水流等环境的干扰在很大程度上影响着机器人的运动控制性能，进而影响跟踪精度[137]。

针对上述路径点跟踪问题，BI等[138]提出了一种路径点跟踪控制系统，该系统包括2层：速度控制层和航向控制层。速度控制层基于实验样机与路径点的距离调节机器人的最大扑动振幅，航向控制层采用模糊控制方法来获得转向运动的转向因子。为了验证控制系统的有效性，进行了路径点跟踪实验，实验结果表明，在任意设置路径点或随机给定路径点的情况下，实验样机均能自主游动到达目标区域；WANG等[122]提出了基于有限状态机（Finite State Machine，FSM）的视线（Line of Sight，LOS）制导系统的路径点跟踪方法，基于RobCutt-I实现了6个路径点的跟踪。

针对上述路径跟踪问题，WANG等[139]提出了一种用于三维点跟踪的切换控制方法，并设计了一个模拟实际水下作业过程的实验。实验结果表明，RobCutt-II能够跟随参考路径，且最大交叉轨迹误差为0.1 m。随后[140]，在该方法的基础上进行改进，提出了一种将视觉系统与反步控制相结合的路径跟踪方法。仿真和实验结果表明，RobCutt-II能够在水下空间中自主地沿着直线和圆形路径游动。此外，与传统比例–积分–微分（Proportion-Integration-Differentiation，PID）方法相比，该方法减小了轨迹交叉误差，轨迹跟踪效果更加理想。同时，由于采用了航向补偿，该方法具有较强的抗干扰能力。

4.5 避障与自主游动

水下扑翼机器人的高机动性使它们能够在复杂和狭窄的环境中工作[141-142]。同时，自主工作的前提条件是机器人能够自主检测和避开障碍物。

目前，水下扑翼机器人大多采用红外传感器[141，143]、超声波[144]、摄像头[142]进行障碍物的检测。ZHANG等[126]综合昆虫翅膀和鱼鳍的优点开发了一款仿生机器鱼，其头部安装了3个对前的红外传感器，包括上前、中前、下前3个方向，利用3个红外传感器的信息作为CPG网络的反馈，机器人可以通过改变步态或动作来避开障碍物，实现自主游动。Festo公司仿生学团队[144]设计Bionic Fin Wave的灵感来自于波浪状鳍鱼类的运动，该自主水下机器人能够与外界进行无线通信，并将传感器记录的温度和压力值等数据传输到电脑上。此外，机器人前部还装有压力传感器和超声波传感器以不断地测量其与障碍物之间的距离，从而防止其与障碍物发生碰撞。XIE等[145]针对仿蝠鲼机器人自主游动的问题，在利用胸鳍相位差进行左右转的基础上引入饱和函数，使得机器人能够根据障碍物的距离改变转弯的速度。YANG等[146]针对已知结构化环境下的绕池壁自主游动问题，采用基于CPG、模糊控制与策略的控制方法，完成了仿蝠鲼机器人的水池绕壁自主游动。

4.6 基于相似度的运动参数优化

随着水下扑翼机器人研究的深入，机器人在模仿真实生物时的重点由“形似”逐渐过渡到追求“神似”[147]。通过提高仿真度，可以显著提升仿生机器人的稳定性、机动性和游动效率[84]。为了解决如何提高机器人运动姿态仿生相似度的问题，亟需建立基于仿生水下机器人的相似度评价体系，有效改善仿生机器人的运动特征和控制策略，进行机器人的运动相似度参数优化。

基于上述问题，MA等[148]通过特征点轨迹提取和动态时间归整（DTW）算法建立了运动姿态的相似度评价规则。通过引入偏置方程和时间非对称系数，建立了表征蝠鲼胸鳍运动时间和空间非对称性的相位振荡器模型，构造了基于相位振荡器的CPG拓扑网络。在此基础上，建立了运动姿态相似度的适应函数，并提出了CPG网络参数的遗传粒子群优化算法，通过水池实验验证了基于相似度优化运动参数优化的控制的有效性。实验结果表明，优化后的仿蝠鲼机器人前游运动姿态与蝠鲼的相似度提高到88.53%；随后，该团队研究了仿蝠鲼机器人胸鳍鳍条相位差变化的优化方法[149]，以输出信号的平滑性和快速性为优化目标，采用非支配排序遗传算法（NSAG-II）对CPG参数进行优化，得到最优参数组合。仿真和实验结果验证了优化后的CPG控制器输出信号在相位切换过程中能够平稳、快速地转换。水下仿生扑翼机器人近年来发展情况如表1所示。

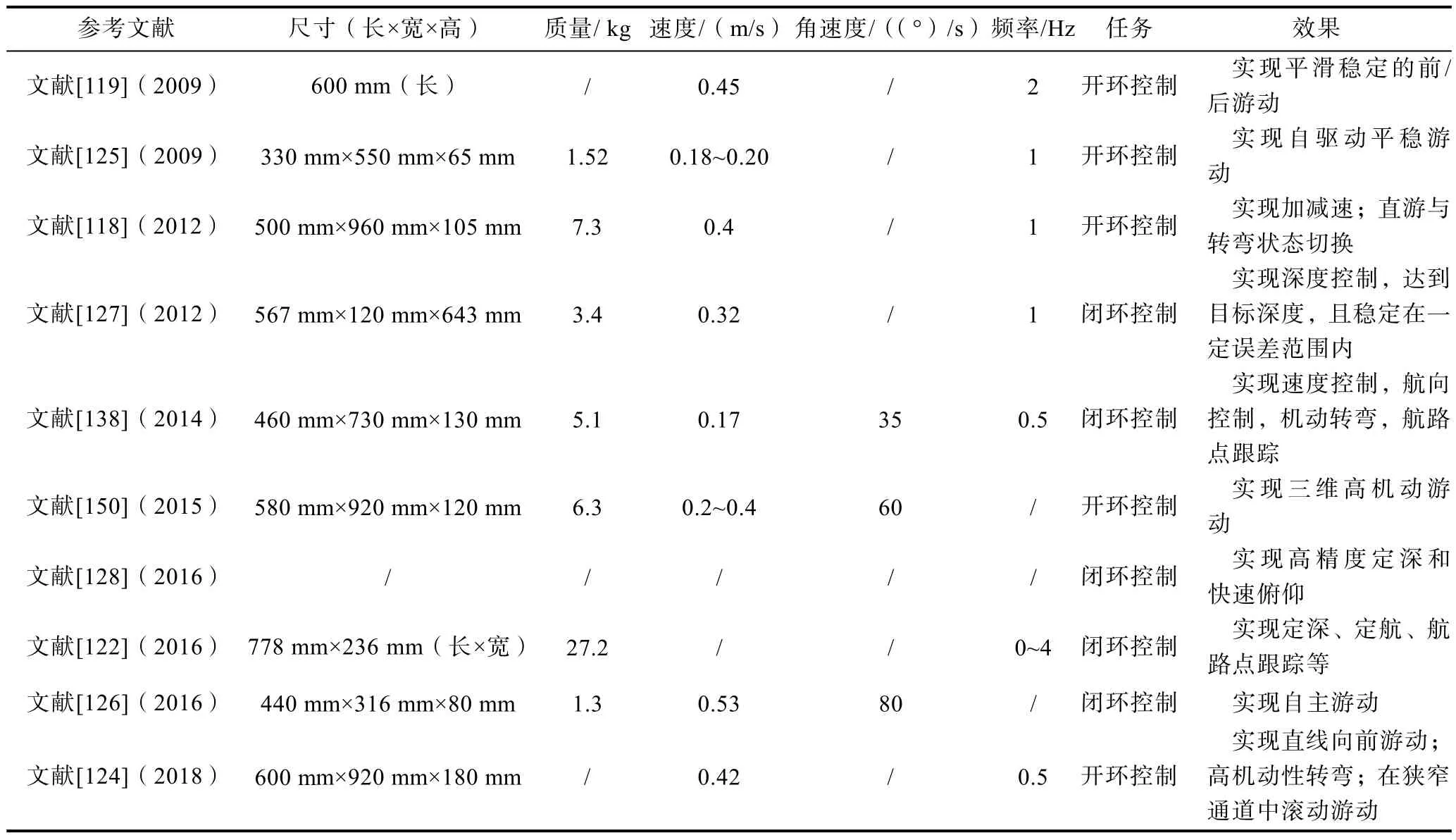
表1 水下仿生扑翼机器人近15年发展情况概述Table 1 Overview of the development of underwater bionic flapping wing robots in recent 15 years

综上所述，基于CPG模型的方法被越来越多地使用到水下仿生扑翼机器人的胸鳍驱动上，该模型能够在简单的激励输入下模拟复杂的节律信号，具有很强的环境适应性，将传感器信息耦合进CPG模型是水下仿生扑翼机器人扑翼驱动控制研究的新方向。在此基础上，研究人员针对水下扑翼机器人的深度与航向控制问题，基于传感器反馈采取合适的控制策略或无模型控制方法，通过改变水下扑翼机器人的俯仰与转弯状态实现深度与航向调节，从而实现深度与航向的控制。进一步地，水下扑翼机器人的路径跟踪与自主游动还需考虑机器人动力学模型的非线性与环境的不确定性，因此目前的研究成果多集中于单平面内的路径跟踪，而三维空间内的跟踪问题仍处于初始阶段。另一方面，仿生相似度评价方法的研究主要集中在仿生陆地生物和仿生机器人，对于运动机构具有明显的主被动变形的水下扑翼机器人，完整的相似度评价体系还有待建立，且基于仿生相似度的运动姿态优化也存在较大的研究空间。未来，水下仿生扑翼机器人的多载荷应用、任务规划与执行将是其成为海洋重要装备的关键，其所涉及控制问题也值得研究人员去探索。

5 水下仿生扑翼机器人集群

与常规推进方式相比，鱼类游动具有更高的效率、机动性、生物亲和性和隐蔽性。近些年来，仿生集群逐渐成为水下机器人领域的一个研究热点。

STEVENS等对蝠鲼种群进行了长达数十年的个体记录与行为观察，详细阐明了蝠鲼个体与群体行为特征，根据蝠鲼的个体数量与运动类型，总结了蝠鲼个体与群体捕食策略，对于了解蝠鲼个体与群体行为特性提供了重要依据[151]。

GAO等和MA等采用数值模拟的方法研究了串联、并排与垂直队形下距离与攻角对蝠鲼个体与整体滑翔水动力性能的影响。从阻力性能方面，双蝠鲼的串联与并排队形可以显著降低整体阻力；垂直滑翔中，随着攻角的变化，个体获得阻力交替减小的效果。在升力性能方面，无论何种排列方式，滑翔时的整体升力与单体升力基本相同[152-153]。

国内外一些机构针对仿蝠鲼机器人的集群控制开展了相关研究。德国EvoLogics公司研发了BOSS-Manta Ray，搭载多型传感器，技术成熟度较高。采用水声通信方式，实现了3台以上BOSS-Manta水下组网与集群，如图9（a）所示，具备水文信息剖面测量、海底绘图、协同监测和搜索等作业能力[154]。2021年，浙江大学设计了由介电弹性体和伺服电机混合动力驱动的软体蝠鲼机器鱼，并提出了一种基于全局视觉定位的机器人集群系统，实现了对自然界生物平行、围捕和环绕3种典型的群集行为的模仿[105]。2022年，北京大学喻俊志团队提出了一种基于视觉的仿蝠鲼机器人水下跟踪方案，采用基于颜色的水下目标识别与定位方法，解决了机器人距离控制与方位控制耦合的问题，并通过水下实验验证了跟踪方案的有效性和鲁棒性[155]。2023年，西北工业大学将仿蝠鲼机器人的跟随问题转变为导引问题。基于鱼群行为启发，制定了基于跟随区域划分的群游跟随导引策略，利用水下动作捕捉系统实现了仿蝠鲼机器人的跟随游动控制[156]，如图9（b）所示。

图9 仿蝠鲼集群控制研究现状Fig.9 Swarm control of manta ray-inspired vehicles

由于水下环境对感知和移动带来了巨大挑战，传统的地面通信方法（如无线电）在水下表现不佳，而GPS等定位方法不可用。同时，水下移动面临速度与加速限制等问题。目前，水下仿生扑翼机器人集群研究仍处于初始阶段。

6 实验研究

根据研究对象的不同可以将实验研究分为生物游动实验和仿生结构实验。通过活体鱼类尾迹流场实验研究了解鱼类游动特性，可为水下仿生结构设计奠定基础；通过水下仿生结构实验验证结构性能，可为优化水下仿生结构提供参考。本节将对生物活体、仿生鳍结构以及仿生机器人的水动力与流场观测实验的研究进展进行回顾。

6.1 生物游动实验

目前已有的生物游动实验研究主要集中在利用粒子图像测速（Particle Image Velocimetry，PIV）方法对BCF鱼类的尾迹结构研究。PIV方法[157]通过高速相机捕捉待观测区域示踪粒子的速度场信息分析得出涡场结构。根据拍摄粒子运动的高速相机的数量，可将PIV实验方法分为二维PIV实验和三维PIV实验。二维PIV实验最少可通过一台高速相机分析出待观测流场切面中流体质点的两个速度分量信息，称为2D2C[158]方法。当有2台及以上高速相机时，可以进行2D3C和3D3C[159]的PIV流场观测实验。2D3C方法的实验待观测区域仍为平面区域，但可分析出流体质点垂直于观测面方向的法向速度分量。3D3C方法的实验待观测区域为具有一定厚度的三维空间，可分析出观测区域内流体质点的3个速度分量。在重构三维流场的PIV实验中，根据照射光的不同，又分为体光源照射实验和激光断层扫描实验。前者通过捕获区域内所有示踪粒子的运动重构三维流场；后者通过测量若干不同切面的流动，利用插值算法重构三维流场。

1999年，DRUCKER等[160]在循环水槽的基础上搭建了一个PIV观测系统，用于研究翻车鱼胸鳍尾迹的涡结构。为保证观测过程中鱼体与观测区域相对静止，将水槽中的流速设定为翻车鱼的游速。通过对翻车鱼俯视面、纵平面、横截面的流场进行观测，得到了对应的速度场信息。根据DICKINSON等[161]得到的尾迹动力学公式，得出了翻车鱼胸鳍尾迹中涡环的动量角、射流角、涡环直径、涡环面积、平均涡环环量以及涡环动量的大小。2000年，DRUCKER等[162]通过PIV实验研究了冲浪鲈鱼和翻车鱼的游动尾迹涡结构，以揭示导致鱼类游动速度不同的机理。实验结果显示，2种鱼类在不同的游动速度下尾流中的射流角和动量角存在较大差异。2001年，DRUCKER等[163-164]研究了翻车鱼不同鳍尾流的涡场结构。翻车鱼的胸鳍、尾鳍和背鳍对于恒定直游时推力的贡献分别为50.0%、37.9%和12.1%。对于转弯时的侧向力，三者的贡献分别是65.1%、34.9%和0，研究结果说明翻车鱼可以利用背鳍处的涡流来增强推力。DRUCKER等[165-168]针对鱼类游动的PIV实验证明了利用PIV实验方法重构鱼类尾迹流场的可行性，通过分析不同尾涡结构的差异，可以揭示鱼类推进的水动力规律。

2004年，TYTELL等[28，169]利用PIV方法研究了鳗鱼的尾迹结构，并验证了鳗鱼游动尾迹中涡环不连续的猜想。实验结果表明，鳗鱼的尾迹涡结构中，侧向的射流在流场中独立存在，尾部区域具有涡量较大的脉冲射流。

6.2 仿生结构实验

水下仿生结构的实验可以分为力学实验和流场观测实验。胸鳍结构的推力和效率是学者们主要关注的力学性能。根据二维不可压缩流体的无量纲的N-S方程，可以推导得到斯特劳哈尔数（Strouhal Number，St）St=l/τv，此无量纲数反映了结构的特征长度、周期运动频率以及与流体环境的相对速度。因此，在研究仿生胸鳍结构周期性往复拍动的运动场景时，St是主要考虑的无量纲数。

1993年，TRIANTAFYLLOU等[170-171]在循环水槽中搭建了测量振动翼水动力的实验平台，并测得推力系数和效率关于St的变化曲线。实验结果表明，当St处于0.2～0.35时，振动翼的效率达到峰值，这与大多数生物游动时的St范围一致。此外，他们还通过染色法展示了翼板后方反卡门涡街演化的过程。1998年，ANDERSON等[172-174]在Triantafyllou水动力实验的基础上，使用PIV设备进行了振动翼尾迹的涡场结构分析实验。通过对振动翼进行变翼型弦厚比、攻角和振荡角的水动力实验，发现推力系数与St之间存在显著的正相关关系，效率呈现出先增后减的趋势。不同工况的实验中峰值效率对应的St存在差异。PIV的实验结果表明当振荡幅度较小、St处于中低水平时，在半个周期内（上冲程或下冲程），振动翼将脱落出一个单涡（2S）；当震动幅度较大或St处于较高水平时，半周期内振动翼将脱落出一个对涡（2P）。

1998年，KATO[175]根据鲈鱼的外形设计了一个胸鳍扑动仿生样机，胸鳍根部由2个旋转轴垂直的电机连接并驱动。实验结果表明，当2个电机的输出相位差为90°时，胸鳍的推力效率最高。

2003年，READ等[176-178]在可调攻角的翼型水动力实验平台上，进行了翼型关于最大攻角、St和振荡角的水动力实验，并绘制了关于翼板攻角和St的推力系数、效率的云图。推力系数的云图表明，当St和攻角同时增大时，推力系数随之增大并逐渐收敛。效率的云图表明，在低St（St=0.1）下，翼板攻角的可调节范围相对较大；随着St增大至0.2以上时，为保证效率不变，翼板的攻角须急速地下降，在St在0.2～0.6范围内，效率最高可以达到0.6。这一攻角急速下降的现象与飞机机翼的失速效应类似。

2005年，BUCHHOLZ等[179]利用染色法对NACA翼型振荡翼板的尾迹结构进行了研究。染色法的原理是在被测结构物前缘左右两侧及上下两面，分别设计可与外界染色物质相连的小孔，由小孔不断输送染色物质到流场中，染色物质可以显示被测结构物周围的流场变化情况。BUCHHOLZ的实验较为完整地展示了不同观测面下，从翼板脱落的马蹄涡的演化过程，以及涡街在不同截面处的结构。

2008年，GREEN等[180]在Smits振荡翼尾迹结构研究的基础上，通过在翼板的特征点处安装多个压力传感器，捕捉翼板振荡时表面压力的变化。实验结果表明，某一点处压力的变化随着翼板正弦形式的振动呈现出非对称的周期性变化。尾迹涡结构的实验结果表明，当振动幅度增大，或者St增加时，尾涡结构会由2S结构逐渐变化为更为复杂的2P结构，这一结果与ANDERSON的实验结果类似。

2008年，HEATHCOTE等[181]采用断层式PIV方法，进行了不同厚度下NACA翼型振动翼的水动力及尾迹涡结构观测实验。实验结果显示，在不同的St下，随着振动翼厚度的逐渐增加，推力系数与推进效率先增大后减小，推进效率最大值为0.27。PIV实验结果表明，靠近翼根处的截面涡结构与靠近翼梢处的截面涡结构具有较大差异。

2010年，RIGGS等[182]对比了2种不同刚度的硬质NACA翼板和柔性仿太阳鱼鳍板的推进特性。实验结果表明，在不同的振幅和频率下，无论是硬质翼板还是柔性鳍板，仿生鳍板的推力显著高于NACA翼板的推力。在侧向力与推力组成的图中，由于一个拍动周期内力学特性呈现出周期性变化，因此侧向力与推力组成一个封闭曲线。在侧向力相同的情况下，仿生鳍板的推力整体在NACA0012翼板之上。

以上是众多学者对于BCF鱼类和NACA翼型鳍板进行的水动力及流场实验研究，对于MPF推进方式的仿生结构的实验研究出现较晚。

2006年，CLARK[183-184]在上述染色法实验的基础上做了进一步的研究。他们采用具有柔性的PVC材料，参照蝠鲼的外形将翼板的形状调整为类椭圆形。通过多个电机轴并联的方式，在翼面上制造行波。翼的上表面连接红色染色物质，下表面连接绿色染色物质，以此来区分翼在运动过程中上下冲程不同的涡结构演化。尾迹结构分析结果表明，在振动翼板的后方演化出两条上下涡旋方向相反的射流。2009年，CAI等[72，74，125，185]以蝠鲼为仿生原型设计了仿蝠鲼机器人。其内部嵌入了气动结构，由外部气源驱动，游动速度较慢。通过水动力实验，测得该仿生结构的力–St曲线与效率–St曲线。实验结果表明，这些曲线的趋势与之前提到的翼板对应数据的趋势相似。同年，MOORED等[186]以牛鼻鲼为仿生原型设计制作了扑翼机构，为实现波动传递将扑翼沿展向切分为多个相连部分。利用染色法对前后缘脱落的尾涡结构进行分析后，观测到了Clark染色法实验未曾观测到的扑翼前缘脱落涡。

2011年，DEWEY等[187]在Smits染色法测尾迹涡结构的实验基础上，将观测手段改为PIV方法，并将振荡翼板的结构改为具有波动传递的仿蝠鲼胸鳍结构。实验结果表明，St和胸鳍上行波的波长是影响胸鳍后缘涡脱落分裂的主要因素。行波波长减小将促使单个振动周期内脱落的涡旋由单个变为一对，St增加将使得沿出射角脱落的相邻分离涡的距离减小。相比之下，2009年，SCHNIPPER等[188]通过改变振动翼的频率和幅度，捕捉到了尾迹涡旋由2S变为2P、2P-2S、4P、8P的结构演化特性，对应的单个周期内的涡旋数分别为2、4、6、8、16。尾迹涡旋的演化过程为，起始涡在翼型前缘和后缘分别脱落后，不断夹带流体质点使得涡核逐渐增大，在达到形成数之后不再继续增加涡量。

上面提到的“形成数”是涡旋由起始到演化再到涡量不再增加的无量纲时间，由GHARIB等[189]于1998年提出，并由DABIRI等[190]持续发展。考虑振动翼和仿生翼尾迹的涡旋演化场景，影响其尾涡结构演化的关键因素为流场速度和结构物的特征长度。

2014年，牛传猛等[45，191-193]基于牛鼻鲼的外形以及运动规律设计了仿生鱼，并搭建水动力实验平台进行了推力和升力关于振动幅度、频率以及舵机输出角度相位差的实验。实验结果表明，振动幅度与推力和升力之间呈正相关关系，而频率在小于0.8 Hz时与推力之间呈正相关关系，大于0.8 Hz时呈负相关关系，推力效率在St为0.4时达到峰值。2017年，CHEW等[194-196]基于蝠鲼生物外形设计制作了仿生鱼实验平台，胸鳍结构采用单鳍条覆以二维PVC薄膜的形式。在不同胸鳍根弦比、后掠角、鳍条刚度等胸鳍结构参数下进行水动力实验。实验结果表明，根弦比代表的弦向柔性增大时，推力系数变化不大，而效率持续降低；展向鳍条厚度即展向柔性增大时，推力系数在呈现一定增长趋势后迅速衰减；后掠角对于仿生胸鳍的推力系数影响不显著。2021年，XING等[88]以蝠鲼为仿生原型设计了可展弦向波动传递的仿生水动力实验平台，针对仿生胸鳍的2自由度运动，研究了胸鳍振动的幅度、频率、俯仰角度以及初始偏置对于其水动力性能的影响。实验结果表明，在普遍的工况设置下，推力在周期内都呈现出高低双峰，平均推升力在不同的频率设置下与振动幅度呈显著的正相关关系。

针对鱼类和水下仿生结构的实验研究主要分为水动力实验和流场观测实验两类。学者们针对鱼类和仿生结构进行了系列化的实验研究，得到结构特性和运动参数对水动力特性影响的规律。但已有的实验研究主要关注鱼类/仿生结构尾流涡场结构的演化，以及全约束模型的水动力特性和流场特性。仿生结构表面处的流场演化、无运动约束的仿生鳍结构实验研究方面还处于初始阶段。