多仿生机器人协同编队捕获策略

杨 丹，冯世龙，石立伟，郭书祥

（北京理工大学，北京 100081）

0 引言

近年来，随着全球人口不断增加和陆地资源勘探的持续进行，人们开始将眼光转移至海洋。作为海洋资源勘探和开发的得力助手，仿生机器人被广泛应用。仿生机器人受益于生物的高度进化感知系统和智能决策能力，能够模仿水下生物的外形和动作方式，从而更好地适应水下环境中的障碍物等未知因素。它们可以通过柔软和灵活的身体结构，在狭小空间中自如穿行，并有效地避开障碍物，实现更精确的编队搜索任务。此外，仿生机器人可以借鉴生物界中生物群体的协同行为，实现高效的信息交流和协作。它们可以通过模拟生物间的非语言沟通方式，如振动、化学信号等，实现机器人之间的紧密配合和协同行动，提高编队任务的效率和准确性。

现阶段针对单一机器人的编队研究已经相对成熟，而多机协作任务成为了国内外学者们关注的重点研究方向[1-4]。该技术的主要目标是实现多个机器人按照某一编队策略，将目标机器人限制在一定预定大小的区域内，使其无法逃逸，以达到对目标的捕获目的。然而，由于水下环境具有复杂的障碍物和大量的未知因素以及水下机器人形体大小和计算能力的限制，多仿生机器人的编队任务目前依然存在许多困难。因此，进行多仿生机器人协同编队捕获策略的研究具有重要意义。

目前，国内外学者针对多机器人协同编队策略已经开展了大量的研究。路径规划部分，陈铭治和NI等[5-6]采用神经网络模型，通过改进神经元的权值来使其更加适用于实时路径规划，但该算法需要大量的计算，对机器人计算性能具有较高的要求，不适用于小型水下仿生机器人。陈世健和赵文瑜等[1，7]采用BUG2算法，使机器人朝目标做直线运动或绕障碍物的靠边运动，以移动到目的地，但该方法规划出的路径不一定具有最优性，无法保证路径长度最短。YU等[8]将RTT*算法进行改进，提出一种Cyl-HRRT*算法，通过将状态偏向到圆柱形子集来引导采样和扩展，以改善当前解决方案。虽然该算法考虑到小型球形机器人的机械结构和自身动力学的限制，但反而会增加算法复杂度，导致计算效率降低。

多机器人编队任务的成功关键除路径的最优性外还包括它们之间任务的分配及协调，协调策略的优劣影响任务的整体效率。NI等[6]根据围捕子区域与目标点间的距离进行目标捕获点分配，该策略以距离最近为目标进行贪婪的分配，但会导致不同机器人到各自捕获点的时间差较大，影响整个编队捕捉任务的实时性和效率。刘云辉和陈阳舟等[9-10]采用“角度最小”原则，根据“目标–捕获点”连线与“目标–机器人”连线的夹角最小进行贪婪的分配，但当2个机器人具有相同夹角的情况时，该分配策略会陷入死锁问题。

本文旨在针对上述编队策略及路径规划部分存在的问题提出了一种基于改进蚁群算法的安全域协商编队捕获策略。本文采用动态调整启发式信息素因子的改进蚁群算法，以实现自适应避障的路径规划；采用安全域协商法实现目标机器人周围期望捕获点的实时分配[11]，并保证各机器人到达捕获位置的时间尽量接近，以提高整体任务效率。本文的研究目标是实现多仿生机器人在水下障碍环境中的高效协同编队，具有重要的理论意义和应用价值。

1 问题描述与建模

1.1 多仿生机器人协同编队搜索问题描述

整个问题建立在有边界的多障碍物环境X中，设有n个搜索机器人R＝{R1,R2......Rn}对位置未知的移动目标点u进行捕获。捕获成功的条件为：搜索机器人在目标探测区域均匀分布或将目标围困在环境边界。

1.2 仿生机器人水下运动方程

整个搜索过程中，需要对搜索机器人以及移动目标的运动速度及角度进行控制。设搜索机器人及目标点正常行进速度为v，目标点发现搜索机器人逃逸速度为1.1v。机器人在t时刻的运动模型可表示为下式：

式中：(x(t),y(t))为各机器人在t时刻的位置；v(t)为t时刻的速度；θ(t)为t时刻速度方向；ω(t)为t时刻的角速度。

1.3 目标点安全域位置

在编队捕获任务中，目标点具有逃逸能力，一旦目标点在可探测区域发现搜索机器人的位置，就会以1.1倍的速度进行逃跑行为，为避免该追逐阶段增加捕获成功的难度，引入安全域的概念，在所有机器人均到达所分配给它们的捕获点之前，不允许某一搜索机器人单独进入安全域，以避免目标逃逸。

胡俊等[12]将整体搜索环境采用栅格法表示，将安全域设计为方形，由于本文环境未进行栅格化处理，所以将安全域定义如下[13]：

式中：SD为目标的安全域；(x,y)为安全域内任意一点坐标；(xm,ym)为目标点位置坐标；d为目标机器人可探测范围。

1.4 目标的捕获点模型

在搜索机器人进行目标搜索过程中，若iR发现目标点u的位置，就按照上面所述方法生成目标点的安全域。为防止目标丢失并提高编队捕获效率，第一个捕获点1m应该位于目标机器人速度反方向与安全域的交点，这样可以确保该捕获点上的机器人与目标始终保持一定距离，并最大限度的减少目标逃逸的概率。其余捕获点从1m开始在安全域圆上以顺时针均匀分布，捕获点的总数量与搜索机器人的数量保持一致。同时，为了更好地掌握目标点的动态变化，我们需要不断地更新目标点的安全域，并对已有的捕获点进行必要的调整，以确保任务成功实现。

所期望的捕获点im的位置信息可用式（3）表示：

式中：i的取值范围为(1,2,3,...,n)，(xmi,ymi)为捕获点i的坐标；uθ为目标点的速度方向；iα为捕获点im与捕获点1m之间的夹角。

2 协同编队捕获任务

2.1 安全域协商的围捕点分配策略

根据式（3）得到目标周围期望捕获位置后，需要对捕获点进行分配。在实际应用中，目前常用的捕获点分配策略包括角度优先策略[1]和距离分配策略[14]，这2种方法均基于贪婪原则，分别以最小化搜索机器人与目标位置的角度或最小化距离作为分配依据，实现搜索机器人与期望捕获位置的逐一对应。

图4（a）为按角度优先策略分配捕获点的示意图，该策略可以有效减少搜索机器人与目标位置之间的旋转距离，在一定程度上提高编队成功率，但当搜索机器人的“目标–分配点”与“目标–机器人”角度相同时，该分配策略会造成死锁问题，如图4（b）所示。

图5为按距离最短原则分配捕获点示意图，但该方法只考虑到搜索机器人与目标之间的直线距离，并未考虑到各机器人到达捕获位置的时间不同步问题。

本文利用基于安全域协商法的捕获点分配策略，在使各机器人到达捕获点的时间差较小的条件下使总路径最短。该算法实现步骤如图6所示。

2.2 基于改进蚁群算法的路径规划策略

群智能算法目前已成为受自然启发的热门算法之一，被广泛用于各种经典NP问题的求解中，展现了它优异的性能和广泛适用性[15]。

在群智能算法中，蚁群算法是一种模仿蚂蚁觅食行为的启发式优化算法，该算法计算成本低，对小型仿生水下机器人的路径规划问题具有良好适用性。本文引入启发式信息对传统的蚁群算法存在的易陷入局部最优解以及收敛速度慢等问题进行了改进，以提高路径规划的性能。

在传统蚁群算法中，蚂蚁仅依靠信息素进行路径选择，容易陷入局部最优解[16]。为了使蚂蚁更好地探索整个搜索空间，本文引入启发式信息作为路径选择的辅助条件。启发式信息的计算公式如下：

式中：Hij为从位置i到位置j的启发式信息浓度；Dij为从位置i到位置j的启发式信息距离。

根据信息素浓度和启发式信息，蚂蚁计算下一步每个可移动方向的概率大小。为了保证方向的全面性和计算的便利性，下一步位置j可以是当前位置i上下左右以及斜对角线45°的8个方向之一，距离位置i的长度为机器人的步长，下一步方向j的概率密度可由公式（5）计算得到：

式中：Pij为从位置i到位置j的概率；ijτ为从位置i到位置j的信息素浓度；Hij为从位置i到位置j的启发式信息浓度；Ni表示位置i的邻居集合，共8个位置；α和β分别为信息素和启发式信息的重要程度参数。

随着蚂蚁进行移动以及实际环境中信息素会挥发的情况，设置信息素的更新公式：

式中：ρ为信息素的挥发系数；Δτij(k)为第k只蚂蚁在位置i到位置j的信息素变化量。

因此，路径规划部分的实现流程如图7所示，整体捕获流程如图8所示。

3 仿真结果与分析

本文基于4个搜索机器人以及一个目标的情况对所提算法进行仿真验证。实验分别在有障碍物和无障碍物的2种环境下进行，由于无障碍物环境下捕获时路径较短，为使实验结果清晰，将环境大小设置为400 m×400 m，复杂障碍物环境大小设置为800 m×800 m。

除环境大小外，两种情况下进行仿真实验的其余条件均相同，机器人及目标点的半径为10 m，运动速度为10 m/s2，搜索机器人初始位置为（150，150）、（250，150）、（150，350）和（250，350），目标机器人初始位置为（100，50），可探测区域及安全域半径为20 m，更新频率为25 FPS。

下面对本文所提出的策略进行验证，首先对路径规划改进蚁群算法部分参数设置进行说明：信息素重要程度参数α为1.0，启发式信息重要程度参数β为12.0，信息素蒸发系数ρ为0.1，信息素增量参数Q为10.0。在避障判断时，本文充分考虑机器人尺寸大小因素，避免运动中机器人边缘部分与障碍物造成碰撞。图9为无障碍物环境中的仿真结果，首先4个机器人进行分散搜索，当发现目标点后执行追逐和编队策略，最终成功捕获目标。

图10为在不同大小的障碍物环境下的仿真结果，可以看出本文所提策略能够使得搜索机器人在整个任务期间有效躲避障碍物并进行编队达到目标位置。

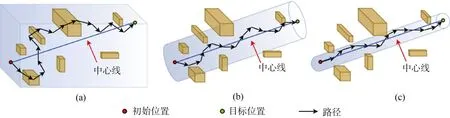
图1 使用Cyl HRRT＊在搜索过程中执行子集收缩[8]Fig.1 Using Cyl-HRRT* to perform subset contraction during search

图2 最终效果示意Fig.2 Schematic diagram of final effects

图3 期望捕获点分配情况Fig.3 Expected allocation of capture points

图4 角度优先分配原则Fig.4 Principle of priority allocation of angles

图5 距离最短分配原则Fig.5 Principle of shortest distance allocation

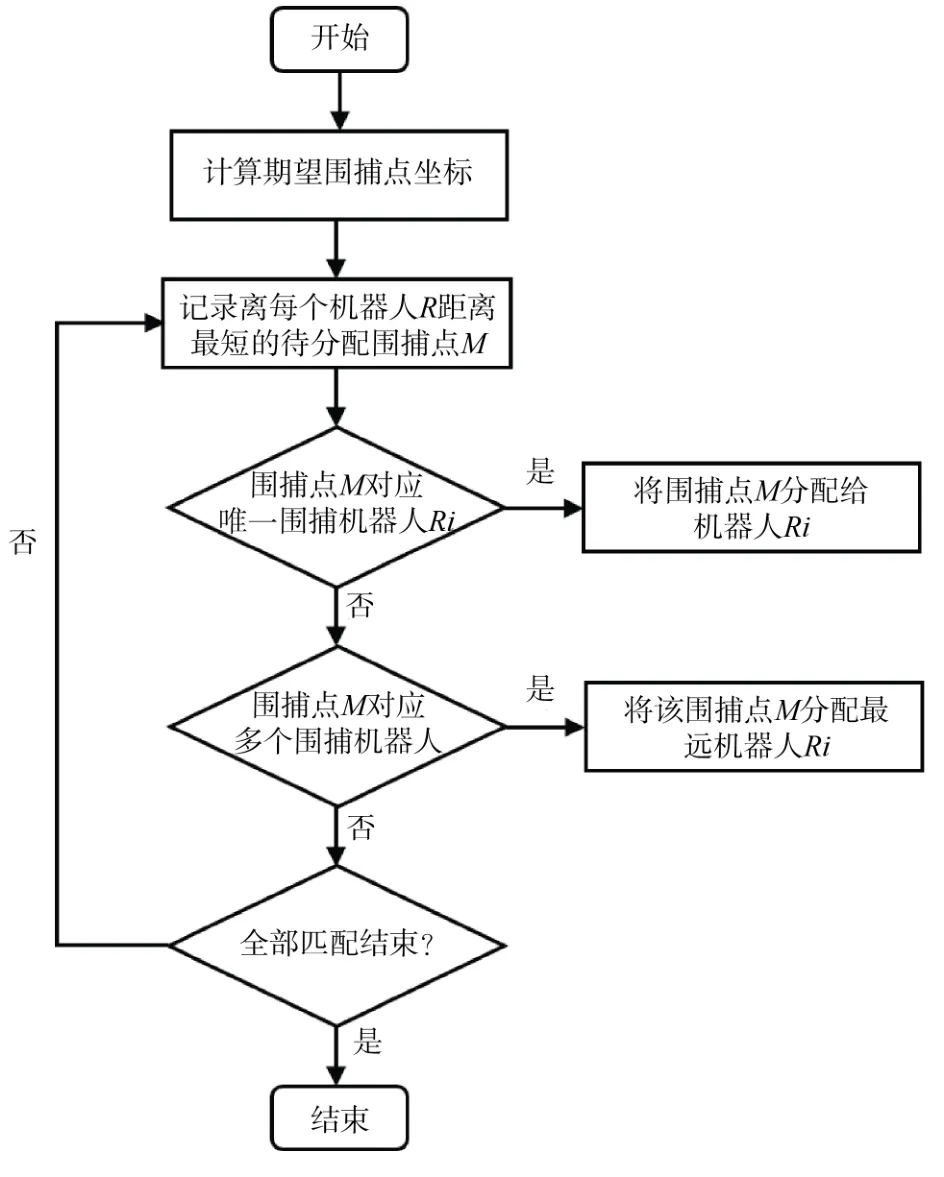
图6 安全域协商分配算法流程Fig.6 Security domain negotiation allocation algorithm process

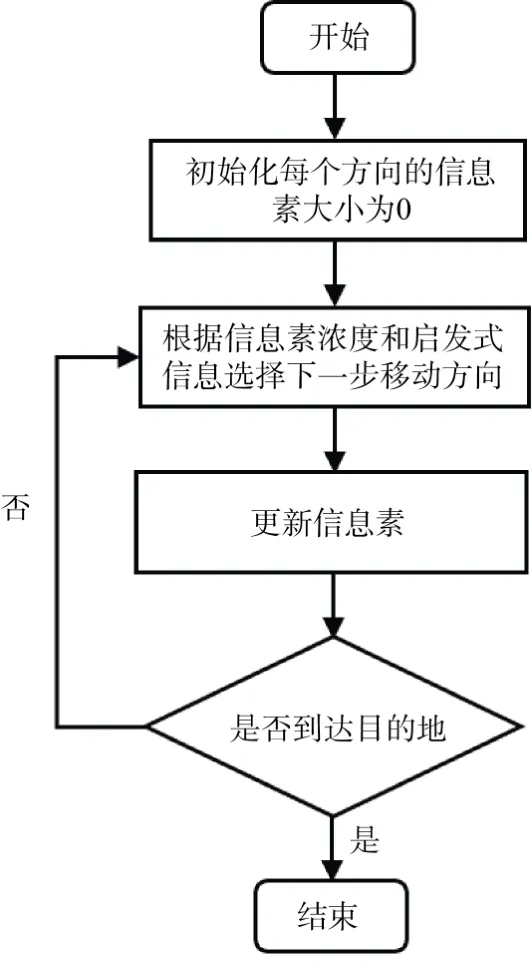
图7 改进蚁群算法流程Fig.7 Improving ant colony algorithm

图8 整体实现流程Fig.8 Overall implementation process

图9 无障碍物环境仿真结果Fig.9 Simulation of obstacle free environment

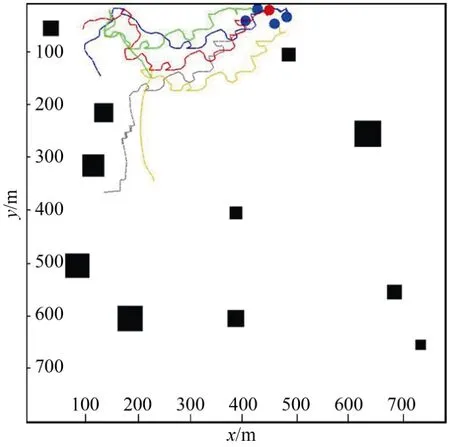
图10 不同大小障碍物环境仿真结果Fig.10 Simulation results of obstacles of different sizes

为对路径规划算法进行评估，本文在初始位置与障碍物位置完全相同的环境下，将改进蚁群算法与改进人工势场算法进行比较。图11（a）、（b）分别为无障碍物环境下以及复杂障碍物环境下基于改进人工势场算法编队搜索结果。

图11 改进人工势场仿真结果Fig.11 Simulation results of improved potential field

此外，我们将算法耗时及成功率作为性能指标进行量化分析，由于蚁群算法为随机性算法，为使结果更具说服力，本文进行了多次仿真实验。下面结果均为取自40次试验结果的平均值。表1为无障碍物和随机生成障碍物环境中2种算法耗时情况的对照结果。

表1 不同环境下2种算法耗时情况Table 1 Time consumption of 2 algorithms in different environments

机器人捕获时间大于25 s视为任务失败，表2为不同环境下捕获目标点成功率的对照结果。

表2 不同环境下2种算法捕获成功率Table 2 Success rates of 2 algorithms in different environments

从表2中的数据可以看出，在2种环境中均是使用改进蚁群算法规划出的航迹长度更短，运行平均耗时更小，尤其在多障碍物环境中，本文所提出的策略会表现出更高的捕获成功率，能够更好的完成任务。对比结果表明：本文所提出的协同编队策略整体具有较优的性能，能够有效地解决二维复杂水下环境中仿生机器人的协作编队捕获任务。

4 结束语

在多仿生机器人系统水下环境中，协同编队策略是解决目标对象追踪和捕捉的关键问题之一。由于水下环境的复杂性和不确定性，传统的捕捉策略在实际应用中充满着挑战。本文旨在提出一种基于安全域协商各改进蚁群算法的编队策略，以解决多机器人的协同捕捉问题。

为了提高任务成功率，建立目标点位置的安全域，并采用安全域协商策略实现对期望捕获点的实时分配，在此基础上，采用改进的人工蚁群算法实现机器人到捕获位置的路径避障规划。仿真结果证明：该协同编队算法在二维复杂环境中能够成功实现对目标点的编队捕捉且具有较好的性能表现，对实际海洋资源探测和机器人编队搜索任务具有参考意义。后续将对三维环境中的算法性能需要进一步探究，并针对实物仿生机器人展开实验。