快速液动网络仿水母软体机器人的结构优化

于 添，吴校生

（上海交通大学 微米/纳米加工技术国家级重点实验室，上海 200240）

0 引言

水母的分布范围和深度广，存在于在热带、亚热带、浅水区、深水区、淡水区等多种水域环境，具有很高的环境适应性。水母在运动时，利用体内喷水反射前进，在较低运动能耗下，可以实现快速漂浮，具备高效、灵活的运动机制。仿水母机器人拥有广泛的应用前景[1]，如：水下摄影、水质检测、探测避障、军事侦察、药物运输等。

早期的仿水母软体机器人主要以刚性材料为主，如美国弗吉尼亚大学的MARUT等研制的Cyro仿水母机器人[2]，Cyro有8个电驱动的刚性机械臂，在机械臂外部包裹人工中胚层以增强整体机构的推进力。近年来，针对仿水母机器人的研究主要以软体结构为主。此类机器人以柔性较大的材料作为主体，具有更大的自由度及更高的灵活性。如何驱动软体材料来实现运动的传递是软体机器人研究的核心内容之一[3]。由于功能材料的多样性，驱动方式也各有不同。德国马克思·普朗克智能系统研究所ZIYU REN等使用磁性复合弹性体设计了一种微型水母，大小仅几毫米，可以在不同磁场下可以实现推动、捕食、物体操纵等功能[4]。福州大学尹超等采用水凝胶–聚（N–异丙基丙烯酰胺）/碳纳米管（PNIPAM/CNTs）研发了一种可见光驱动的微型水母（直径约2 cm），他们通过调整光照焦点位置来控制机器人的运动方向[5]。美国弗吉利亚理工学院的JOSEPH NAJEM等利用离子交换膜金属复合材料（IPMC）作为驱动器制作出一种仿生水母[6]，通过直接加载电压使其发生弯曲形变以达到喷射推进的效果。哈佛大学WHITESIDES研究团队制作了一款多驱动器的软体机器人，该机器人仅使用5个驱动器及一个简单的气动阀门系统，即可在低压（< 10 psi）下运行[7]。该团队基于此结构进一步提出了快速流动网格结构[8]（Fast Pneumatic Network，FPN），并将前一种驱动器命名为慢速流动网格结构（Slow Pneumatic Network，SPN）。此类驱动器的腔室由一条中空的通道相连接，当驱动器发生膨胀时，驱动器向约束侧弯曲。FPN结构相较于SPN结构，每个腔室都是完全独立的，除通道与约束侧相连外，没有其它约束。这种设计使得弯曲效果更加明显。

当前，针对仿水母软体机器人的研究主要围绕2个方面：一类是通过外驱动来实现机器人的运动控制，即采用机器人体外引入的能量源来激发机体的运动，典型驱动方式有电磁驱动[4]和光驱动[5]。体外驱动机器人具备体积较小，运动灵活等特点，但它依赖于外围环境中的磁场、光源，难以独立运行。另一类是采用机器人体内外流体（气体或液体）交互来实现机体的运动，如FPN结构驱动机器人[8]。此类机器人体积相对较大，通过泵结构与环境交互增压实现偏转弯曲，但需与外环境的连通，抗压能力、灵活性和稳定性相对较差。

本文提出了一种全封闭的仿水母软体机器人结构模型。该机器人采用快速流动网络（FPN）构建驱动结构，采用电推杆推动密封液体来实现仿水母软体机器人外伞摆动。该结构具备全封闭的网络结构，无需与外界环境进行介质交互，密封结构具有更强的抗压能力和稳定性。相比于泵结构，电推杆更能满足独立驱动需求。通过集成控制电路和电源模块，可以实现机器人的自主控制。该机器人具有紧凑的系统结构。

本文内容包括：仿水母软体机器人结构设计及工作原理介绍，软体机器人动力学分析，结构参数优化设计，机器人的制造以及驱动装置构建，系统集成及性能测试。

1 仿水母软体机器人的结构

仿水母软体机器人的总体设计如图1所示。图1为仿水母软体机器人模型，其中图1（a）为空间视角图，图1（b）为其剖面图。总体结构包括：外伞、活塞及活塞腔室、电动推杆、控制电路以及电源，共5个部分。

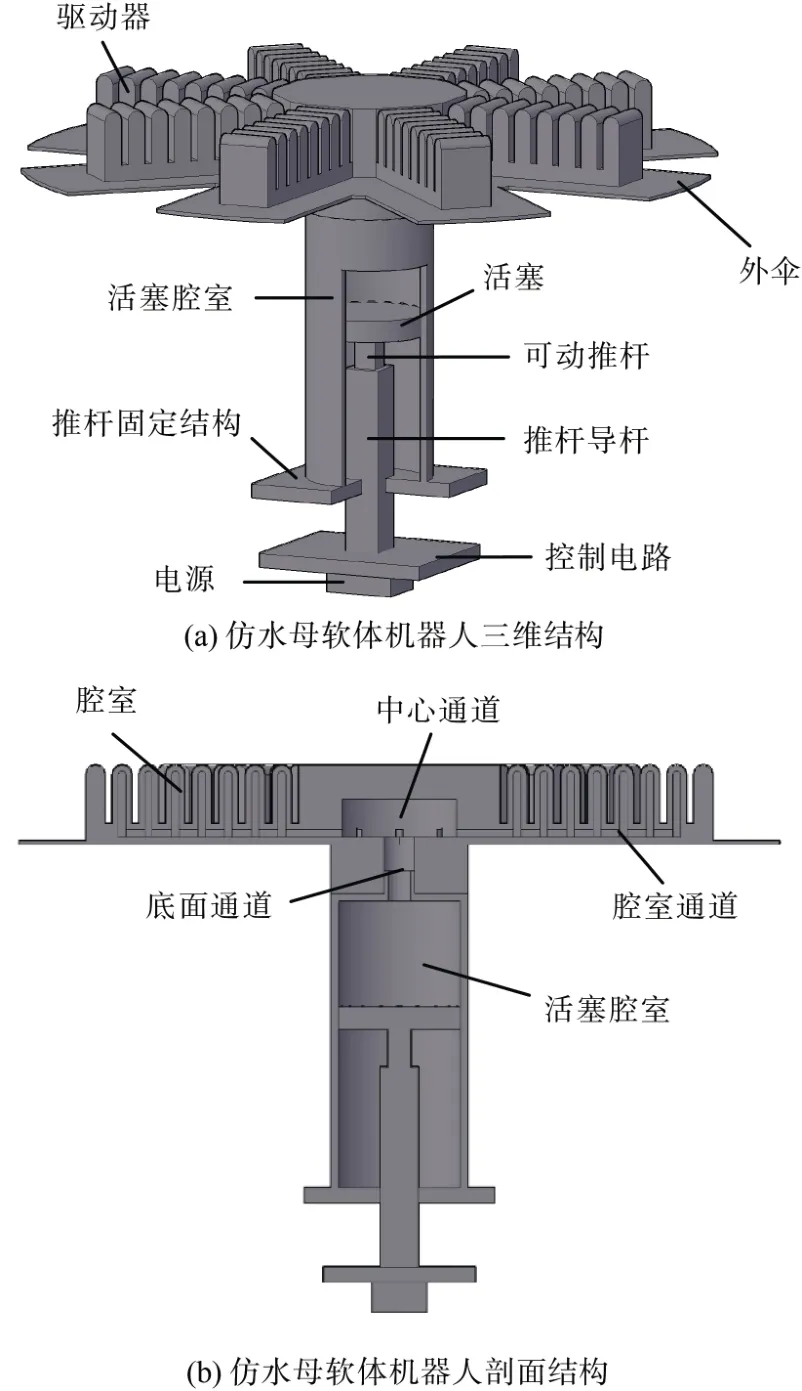
图1 仿水母软体机器人的总体结构Fig.1 General structure of soft jellyfish-like robot

外伞采用超弹性材料制作，是仿水母软体机器人的主体，它由8个驱动器在圆周方向上轴对称等距分布构成。每个驱动器上分布有多个腔室等距排列，并通过内部的腔室通道连通起来。中心通道将8个驱动器连通在一起，并通过底面通道与活塞腔室相连。

仿水母软体机器人工作时，电推杆带动活塞的上下运动以控制活塞腔室内的空间大小。电推杆为仿水母软体机器人的驱动部件，为仿水母软体机器人提供驱动能力。控制电路模块设置电推杆的运动方向与运动速度。纯超弹性材料结构刚度较小，在重力作用下外伞结构难以独立支撑，为了增强外伞的支撑刚度，在外伞底部嵌入弹簧钢片。该设计有利于增强系统对外界流体扰动的抗干扰能力。

2 软体驱动器结构设计与优化

仿水母软体机器人外伞采用超弹性材料制作。为优化模型的结构参数，需要引入超弹性材料的本构模型。超弹性本构模型主要分为基于连续介质唯象理论的本构模型和基于分子链网络的本构模型2种[9]，其中连续介质唯象理论是通过建立材料的应变能密度函数表达式来描述材料性质。假定为各向同性且不可拉伸的超弹性材料，应变能密度函数可以表示为

其中：

式中：W为应变能密度；1I，I2，I3为Chausy-Green变形张量的不变量；1λ，2λ，3λ分别为轴向、径向、周向的伸长比[10]。

研究表明，Yeoh模型可以较好地模拟材料在大应变时的特性[11]。Yeoh模型的表达式为

式中，C10，C20，C30为材料参数，可通过单轴拉伸试验数据拟合获得。

Yeoh模型具有形式简单、精确度高的优点，本研究选择Yeoh模型完成COMSOL的仿真工作。

超弹性材料采用Ecoflex 00-30[12]，材料参数为：C10＝1.0×10-1MPa ；C20＝1.2×10-2MPa ；C30＝4.96×10-5MPa 。

为简化研究模型，先对软体驱动器进行分析，本研究选用FPN结构来构建软体驱动器。如图2所示，驱动器由多个相同的独立腔室在同一水平方向上等距线性排列，通过腔室通道将各腔室连通起来，底部作为限制层。在仿真过程中，对驱动器左侧平面进行全约束。图3给出了驱动器的结构参数，其中图3（a）为周向剖视图，图3（b）为径向剖视图。驱动器包含以下结构参数：腔室宽度w、腔室高度h、腔室壁厚t、腔室数量n、驱动器底面厚度b、驱动器长度l，通道宽度r。在加压过程中会在限制层侧发生形变，随着驱动器内部压强的逐渐增大，弯曲的弧度也会随之增大。

图2 软体驱动器外观结构Fig.2 Structure of a soft actuator

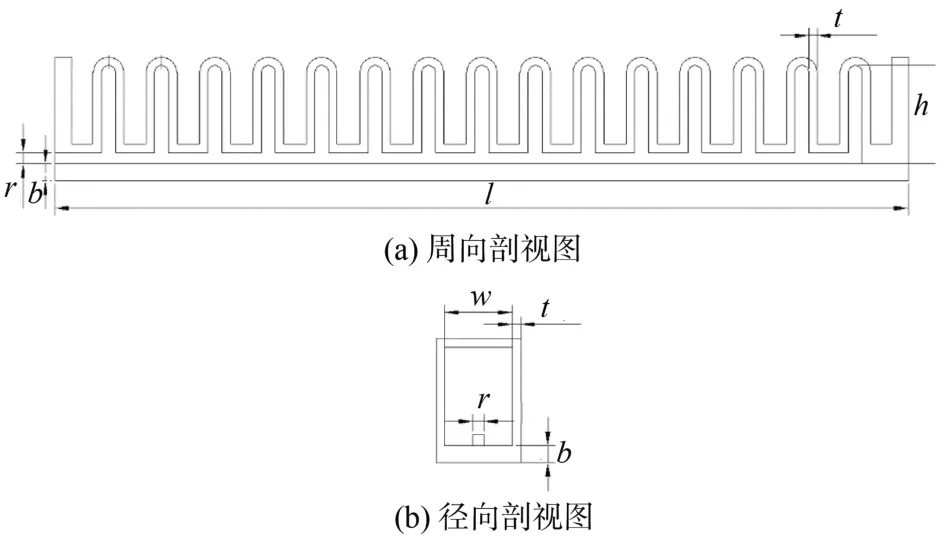
图3 软体驱动器结构参数Fig.3 Structural parameters of a soft actuator

图中：腔室宽度w、腔室高度h、腔室壁厚t、腔室数量n、驱动器底面厚度b、驱动器长度l均会影响驱动器的偏转角度。为了获得最大偏转角的软体驱动器尺寸参数，将采用控制变量法，对不同参数进行有限元分析。

2.1 驱动器尺寸参数优化设计

如图4所示，采用控制变量法对腔室宽度w、腔室高度h、腔室壁厚t、腔室数量n、驱动器底面厚度b、驱动器长度l分别进行有限元分析，研究不同参数下偏转角度随压强增大时的变化规律。

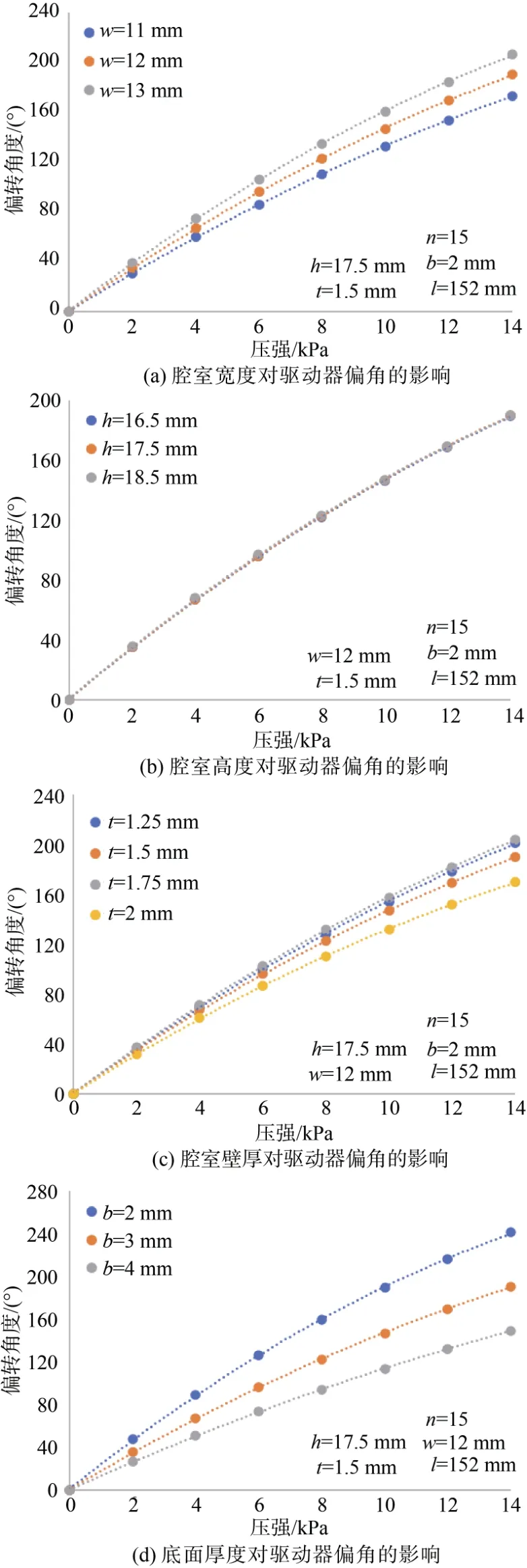
图4 驱动器尺寸参数对驱动器偏转角度的影响Fig.4 Influence of size parameters on actuator deflection angle

图4（a）给出了腔室宽度w对驱动器偏角的影响规律，结果表明，较大的w有利于增大偏转角度。图4（b）给出了腔室高度h对驱动器偏角的影响规律，结果表明，h的变化对驱动器偏角基本无影响。图4（c）给出了腔室壁厚t对驱动器偏角影响规律，结果表明，t从2 mm降至1.25 mm的过程中，偏转角先变大后减小，在t=1.75 mm时可获得最大的偏转。这是由于在仿真过程中固定了腔室间的间距，t变大导致腔室之间的间隙变小，当t=1.75 mm时相邻腔室在膨胀过程中接触在一起，使得偏转角增大。图4（d）给出了驱动器底面厚度b对驱动器偏角的影响规律，b越小有利于提高偏转角。b值不能太小，它会影响驱动器的整体刚度和强度。图4（e）给出了腔室数量n，即驱动器间间距对驱动器偏角的影响规律，腔室越多，驱动器自由度越大，相同压强下的驱动器偏角越大。图4（f）给出了驱动器长度l对驱动器偏角的影响规律，l越大驱动器偏角越大。

从图4中不难发现，腔室宽度w，驱动器底面厚度b，驱动器长度l，腔室数量n对驱动器偏角的影响相对较大。仿水母软体机器人的优化设计就是要在给定的外形尺寸约束下寻找最优的尺寸组合，以获得最大的驱动器偏转角。

2.2 仿水母软体机器人外伞有限元分析

表1为仿水母软体机器人外伞的尺寸参数，各参数是依据上述驱动器分析结果来选择的最佳组合。如图5所示，仿水母软体机器人外伞由8个驱动器在圆周方向上轴对称等距分布构成，中心通道将8个驱动器连通在一起。为增大驱动器与水之间的相互作用力，在驱动器底部增加一外延层，外延层的宽度比驱动器底部尺寸大。对相邻驱动器外延层之间进行裁剪，以减小应力集中以及驱动器弯曲变形刚度。图5（a）为外伞的顶部视图，图5（b）为外伞的底部视图。

表1 仿水母软体机器人外伞的设计参数Table 1 Design parameters for the outer umbrella mm

图5 仿水母软体机器人外伞模型Fig.5 Model of the outer umbrella

在驱动器底部增加外延层以后增大了驱动器的偏转刚度，为了研究外延层对整体结构的影响规律，我们对比了驱动器与外伞在不同压强下的偏转角度，如图6所示。分析中采用的外延层厚度为1 mm，增加外延层以后，外伞的偏转角确实比驱动器偏转角要小，但影响不大。

图6 外伞和驱动器偏角随压强变化曲线Fig.6 Deflection angles of outer umbrella and actuator at different pressures

2.3 弹簧钢片的有限元分析

由纯超弹性材料构建的外伞结构刚度很小，在重力作用下难以形成对整体的支撑。为了提高结构的支撑刚度，我们在驱动器底部内嵌了弹簧钢片。增加弹簧钢片虽然能够提高结构的支撑刚度，但对外伞的偏转角也会有影响，因此选择合适的弹簧钢片厚度和形状很重要。为了增大外伞的支撑刚度，同时还尽量减小驱动力对外伞摆动的影响，我们将弹簧钢片外形设计成锯齿状。设计中将弹簧钢片的厚度限定为0.2 mm。锯齿形弹簧钢片外形如图7所示，长度d为56.5 mm。以O为原点构建平面坐标系，A为锯齿的外角点，其坐标为（xA，yA），B为锯齿的内角点，其坐标为（xB，yB）。限定A、B间的水平距离（xB–xA）为1 mm，A和B点处的倒角半径为0.3 mm。

图7 弹簧钢片Fig.7 Steel sheet spring

内、外角点A、B的位置决定了弹簧钢片的锯齿大小以及刚度。图8分析了在限定齿间距（xB–xA）为1 mm时，yA和yB取不同值的时候，驱动器偏转角度的变化规律。通过与图6的结果进行比较，可以发现弹簧钢片的引入虽然能够增加驱动器的刚度，但偏转角度也发生了大幅的降低。本研究选择yA=7.5 mm，yB= –1 mm，此参数下驱动器具有较大的偏转能力。

图8 内嵌不同弹簧钢片驱动器偏角随压强变化曲线Fig.8 Deflection angles of actuators with different steel sheet springs at different pressures

3 仿水母软体机器人外伞的加工

仿水母软体机器人外伞的加工采用金属模具进行浇筑成型。为了形成封闭的腔室结构，将外伞结构分成两部分进行加工，分别为底部的限制层（图9（a））和上层腔室部分（图9（b））。图9（a）中的限制层模型制作采用了多次浇铸法，方便将弹簧钢片嵌入到其内部。图9（c）是将腔室部分和限制层模型粘合在一起的效果图。

图9 仿水母软体机器人外伞的制作Fig.9 Manufacture of outer umbrella

4 仿水母软体机器人的驱动及水下实验结果

图10是本文提出的一种全封闭的仿水母软体机器人结构模型。该结构具备全封闭的网络结构，无需与外界环境进行介质交互，密封结构具有更强的抗压能力和稳定性。通过活塞的运动，可以改变仿水母软体机器人外伞内介质的体积。本文研究的仿水母软体机器人用于水下作业，因此介质选择与环境介质相同的水。当外伞内水体积增大时，由于内部压强增大会使得其膨胀产生形变来承载介质在外伞内的体积增量。

图10 封闭腔室液动结构Fig.10 Closed chamber of hydrodynamic structure

图11给出了外伞偏转角度随腔室体积增大后的实验曲线。从图中可以发现，体积增量为0时，外伞由于在实验中受到环境重力的影响，存在约32°的偏转角度，当体积增量为30 mL时，偏转角度约71°。外伞随腔室内体积增量变化的偏转较为明显，具有较好的偏转能力。

图11 外伞在不同体积增量下的偏转角度Fig.11 Deflection angles of outer umbrella at different volume increments

仿水母软体机器人的自主驱动通过电推杆完成，推杆的往复运动通过改变电流方向实现，控制电路模块设置电推杆的运动方向与运动速度。选用的可动推杆最大运动位移约为16 mm，对应活塞腔室内介质体积变化量约为26 mL。控制电路设置循环周期为10 s，即从初始状态到推杆伸长至最大位移需4 s，保持1 s，推杆收缩至初始状态需4 s，保持1 s。

图12给出了外伞在推杆周期作用下的水外运动变化。在t=0–4 s阶段，活塞向上推动，外伞逐渐膨胀形变，并在t=4 s时形变量达到最大并保持1 s的稳定状态，此时外伞外缘的偏转角度约为65°；在t=5–9 s阶段，活塞向下拉动，外伞的形变量逐渐减小，并在t=9 s时恢复到初始状态，此时外缘的偏转角度约为32°。

图12 外伞的水外测试周期运动Fig.12 Out-of-water testing of the periodic motion of outer umbrella

图13为仿水母软体机器人在负重载荷约100 g时发生的上浮运动。仿水母软体机器人的自重约为473 g。图13（a）为仿水母软体机器人的初始状态，此时推杆处于收缩状态，即腔室内的水没有被挤压进入外伞内腔。当推杆运动时，如图13（b）所示，外伞内部由于受到压力增大发生形变，仿水母软体机器人产生了上浮运动。

图13 仿水母软体机器人的负重运动Fig.13 Weight-bearing motion of the jellyfish-like robot

5 结束语

本文提出了一种仿水母软体机器人结构。机器人采用快速流动网络（FPN）构建驱动，采用电推杆来实现仿水母软体机器人的外伞摆动。论文提出的仿水母软体机器人具有全封闭结构，在机器人运动控制过程中不需要和外界进行物质交换，能实现全自主运动控制。采用有限元法对机器人的结构参数（腔室和驱动器的尺寸）进行优化设计。通过精密加工模具实现了软体结构的制作，采用弹簧钢片对软体结构进行刚度加强，将各部件进行联接，实现了模型的系统集成。实验结果表明，机器人在负重载荷约100 g时（自重约473 g），实现上浮运动。通过对原型机的测试，实现了仿水母机器人水下自主上浮运动，验证了本设计方案的可行性。