笛卡尔网格下精确高效的壁面距离计算方法

孟 爽，周 丹，李雪亮，毕 林，3，*

(1.中南大学 轨道交通安全教育部重点实验室，长沙 410075；2.空气动力学国家重点实验室，绵阳 621000；3.中国空气动力研究与发展中心 计算空气动力研究所，绵阳 621000)

符号说明

0 引言

笛卡尔网格可以不依赖物面网格直接生成，因具有自动化程度高、复杂外形适应性好、非定常/多尺度流动结构捕捉能力强等优势而广受关注[1]。

壁面距离的精确高效计算对实现笛卡尔网格方法具有重要意义：一方面，由于笛卡尔网格的非贴体特性，通常采用虚拟单元法处理物面边界[2-6]，需要根据物面确定虚拟单元的壁面距离，寻找参考点并插值获得其物理量，壁面距离精确计算对虚拟单元物面处理精准度有较大影响；另一方面，对于非定常流动或运动物体，笛卡尔网格会根据流场的变化或物体的运动进行自适应[7-8]，自适应后的网格壁面距离需重新计算，壁面距离计算效率成为制约流动计算效率的关键因素之一。

目前，壁面距离的计算方式主要分为求解偏微分方程[9-12]和采用几何方法直接计算[13-14]两类。第一类方法，将最小距离转换为关于波传播问题的偏微分方程数值求解[15]，需要额外的计算花费，壁面距离计算精度受数值离散精度的影响，且对于复杂外形适应性较差。第二类方法是根据空间点与物面离散网格的几何关系计算壁面距离。通常为简单起见，在物面网格足够密的情况下，求解空间网格点的壁面距离时，一般采用空间点到物面网格中心的距离代替最小距离。赵钟等[16]发现，这种近似距离会引起计算误差，不仅影响计算结果的精度，而且对计算稳定性造成影响。为提高计算精度，有学者发展了根据空间点关于物面网格所在平面投影点与物面网格的几何关系计算壁面距离的3D 投影法[16]、通过坐标变换转化为二维问题的2D 法[17]等，但这些方法涉及大量向量计算和关系判断，计算量较大。

在几何方法求解壁面距离时，由于物面网格数目较大，计算效率的核心问题是如何快速定位到最短距离相关的物面网格，物面网格数据结构是关键。

最常见的方法是将物面网格顺序存入数组，采用遍历法搜索物面点得到壁面距离。网格规模较小时，计算量尚在承受范围之内。但是对于三维复杂几何外形的流场计算，物面网格数量可达到O(105)～O(106)量级，空间网格点可达到O(108)～O(109)量级，采用遍历法计算量达到O(1013)～O(1015)量级。此种规模的计算量对整个计算周期的影响是巨大的。Boger[18]提出采用ADT (alternating digital tree)二叉树数据结构存储物面网格，计算效率大幅提高，成为目前最常用的物面网格数据存储方式。但对于复杂外形，ADT 平衡性下降，计算效率仍然差强人意。郭中州等[14]采用KDT (K-dimensional tree)存储物面网格，解决了ADT 平衡性问题，计算效率进一步提升，但对于离物面较远的空间点，在运用KDT 最近邻搜索算法时，超球面与分割面位置关系判断失准，需要反复回溯，计算量大。

本文针对上述问题，引入三角形参数化方法，将空间点到三角形物面离散网格的最小距离问题转换为约束条件下一维极值问题；同时发展嵌套包围盒概念的KDT 物面网格数据存储结构，优化KDT 最近邻搜索算法中距物面较远数据点回溯过程，实现最小距离对应的三角形的快速定位。

1 点到三角形最小距离精确算法

点到空间三角形最小距离的问题[19]可描述为点P和三角形T(s,t)=B+sE0+tE1之间的最小距离，其中(s,t)∈D={(s,t):s≥0,t≥0,s+t≤1}，B为三角形的一个顶点，E0和E1分别为此顶点对应的三角形两条边。点P和三角形内任一点T(s,t)距离的平方为椭圆函数：

其 中，(s,t)∈D，a=E0·E0，b=E0·E1，c=E1·E1，d=E0·(B-P)，e=E1·(B-P)，f=(B-P)·(B-P)。点P和三角形之间的关系如图1 所示。

图1 点P 和三角形之间的关系Fig.1 The relationship between P and the triangle

最小距离问题转换为在D内求连续可微函数Q(s,t)的极值问题。令：

图2 用三角域D 划分s-t 平面以及不同等高线Fig.2 Partition of a s-t plane by triangle domain D and distance contours

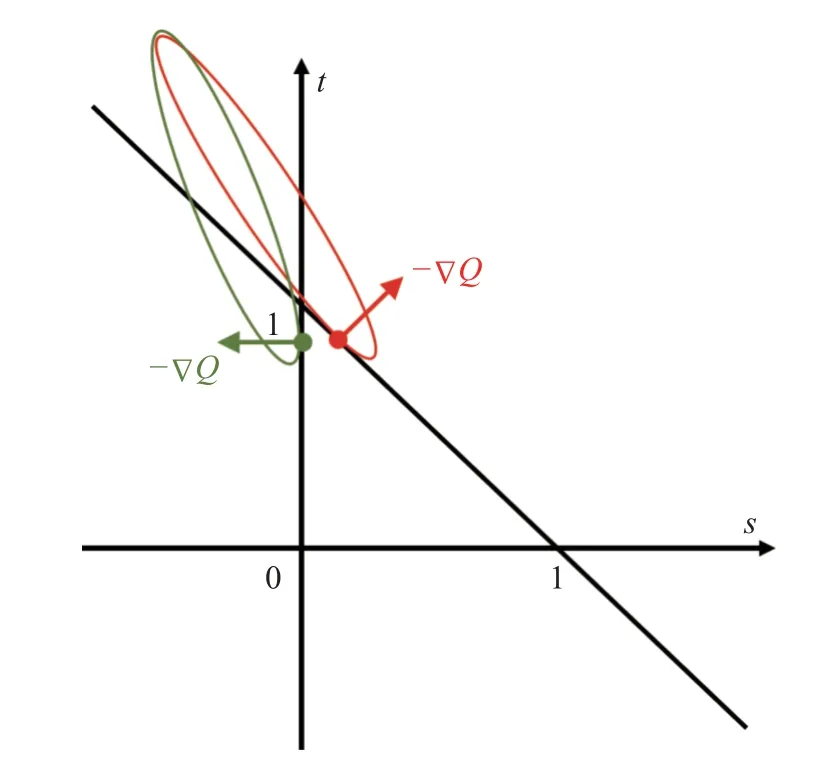
图3 以区域③为中心的等高线与三角形接触的两种情况Fig.3 Two contour levels with centers in region ③touching the triangle

在等值线上的任何一点，-Q的方向均朝向椭圆内部。为简单起见，我们根据-Q沿顶点(0,1)的两条边的方向导数的符号进行判断：

1）对于边s+t=1，顶点(0,1)处的方向导数为如果值为负，最小值出现在边s+t=1上。最小值的情形对应图3 红色曲线，处理方式和s∈[0,1]在区域②类似。

2）对于边s=0，顶 点(0,1)处的方向导数为(0,-1)·∇Q(0,1)。如果值为负，最小值出现在边s=0上。最小值的情形对应图3 绿色曲线，处理方式和 (,)在区域②类似。

2 物面单元的存储

2.1 嵌套包围盒概念的KDT 参数定义

与文献[14]中只存储物面网格中心点不同，本文发展了基于嵌套包围盒概念的KDT，不仅按逆时针顺序存储物面网格顶点信息（方便笛卡尔网格物面处理），还同时包含KDT 节点对应所有物面网格的最小包围盒，KDT 节点从上到下形成嵌套包围盒形式。嵌套包围盒的引入保证KDT 每个节点包含当前节点对应三角形的所有信息，且在最小距离查询时，仅需要通过与剖分面（剖分面的大小由包围盒确定）坐标对比，就可以快速排除与目标点距离大于当前最小距离的三角形，效率大幅提升。

2.2 嵌套包围盒概念的KDT 建立步骤

步骤1：在正式创建KDT 之前，首先需要确定目标数据集G中三角形元素的数量N。然后，需要根据这N个元素确定G的最小包围盒，包围盒的两个顶点分为 (Gimin,Gimax)，其中i=1，2，3，其定义如图4 所示。

图4 几何外形包围盒Fig.4 Geometry bounding box

步骤2：创建一个空的KDT 备用。

步骤3：若N为1，则将此元素插入到当前KDT的节点中去，同时，将此节点的左右子树均置空。

步骤4：若N为2，则将第一个元素插入到当前KDT 的节点中去，同时规定第一维为划分维。此时，只有第二个元素尚未被插入到KDT 中。将第二个元素中心点与第一个元素的中心点在第一维的值进行比较。若第二个元素大于第一个元素，则对当前节点的右子树进行步骤3 的操作，同时当前节点的左子树置空；否则，对当前节点的左子树进行步骤3 的操作，同时当前节点的右子树置空。此步骤中d加1。

步骤5：若N大于2，则首先确定划分维。为了保证KDT 的平衡，划分维的确定是计算N个三角形的中心点Tcenter在各个维度的方差，然后找出方差最大的维度即为划分维。然后将此N个元素中心点在方差最大的维度上按从小到大的顺序进行排序。将位于中间的元素插入到当前KDT 的节点中去。小于此元素的将全部位于当前节点的左子树，大于此元素的将全部位于当前节点的右子树。对当前节点左子树和右子树的元素递归执行步骤3 或步骤4 或步骤5，直至所有元素全部插入到KDT 中。

值得注意的是，在向KDT 中插入节点的同时，节点对应的包围盒也在进行同步划分。例如KDT 根节点对应的包围盒即为数据集G的包围盒 (Gimin,Gimax)。假设节点K对应的包围盒为(Kimin,Kimax)，则K的左子节点KL的包围盒(KLimin,KLimax)为：

由于节点包围盒表示此空间区域内所有三角形元素集合的最小包围盒，而在进行空间区域剖分时的依据是三角形中心点确定的平面，所以节点包围盒与包围盒之间，剖分面与剖分面之间会存在相交的部分。这种相交只会出现在三维及以上的情况。

2.3 创建KDT 时间复杂度分析

由于KDT 是一个二叉树，所以对于给定的N个元素建成一个深度为d的最优KDT 有：

3 最小距离查询

计算空间某点到物面的最小距离需要两个步骤。第一，得到此点到物面最小距离的点所在的物面三角形；第二，采用点到三角形最小距离精确算法得到此点到物面的最小距离。本节基于KDT 最近邻算法对第一步进行设计。

3.1 算法设计

1）首先从KDT 的根节点开始查询，根据目标点与根节点剖分面的位置关系，确定与目标点T潜在的最近点是在根节点的左子树还是右子树。

2）根据1）确定的子树，对此子树的节点进行步骤1）的操作。

3）当递归访问至叶子节点时，记录T与当前节点之间的距离作为当前最近距离lmin，当前节点作为与目标点T最近的节点记为Knearest。

4）进行回溯操作。回溯操作从当前最近的点Knearest开始向上进一步查找。构造以T为球心，lmin为半径的球。若球面与Knearest父节点的剖分面相交，则查找Knearest的兄弟节点即Knearest父节点的另外子树的节点，同时计算T与Knearest父节点之间的距离，若小于当前最小距离，则Knearest和lmin均进行更新；若球面与剖分面不相交，则说明Knearest的兄弟节点中不存在比Knearest与T更近的节点。

5）执行步骤4）直至根节点。得到的Knearest即为与T最近的点，lmin为Knearest与T的最小距离。至此最小距离查询模块结束。

3.2 算法优化

在实际流场计算中，存在空间网格点与物面距离较远的情况，此时采用上述最小距离查询方法将面临回溯操作效率低下的问题。为了直观说明问题，本小节以二维数据点为例进行说明，给定随机分布的17 个点，对这些点创建KDT，如图5 所示。给定目标单元T，正常查找得到的最邻近单元是G。在回溯操作中，以T为圆心，T和G之间的距离lTG为半径的圆与根节点J的剖分轴m相交。根据上述回溯步骤，此时需在J的左子树进行查询。然而，实际情况是圆与J的左子树并不相交。因此，后续的回溯操作均为无效回溯，这将大大浪费计算资源。为此，本文在回溯操作时，首先判断以T为圆心，T和G之间的距离lTG为半径的圆是否与线段ab相交（ab由剖分轴和当前包围盒确定）。若相交，则进行正常的回溯操作；若不相交，则直接排除对应节点另外子树存在最小距离的可能性。采用改进前后的回溯法进行的回溯操作如图5（b～c）中绿色箭头所示。从图中可以看出，改进后的回溯方法可极大减少不必要的回溯过程，进而提高最小距离查询效率。

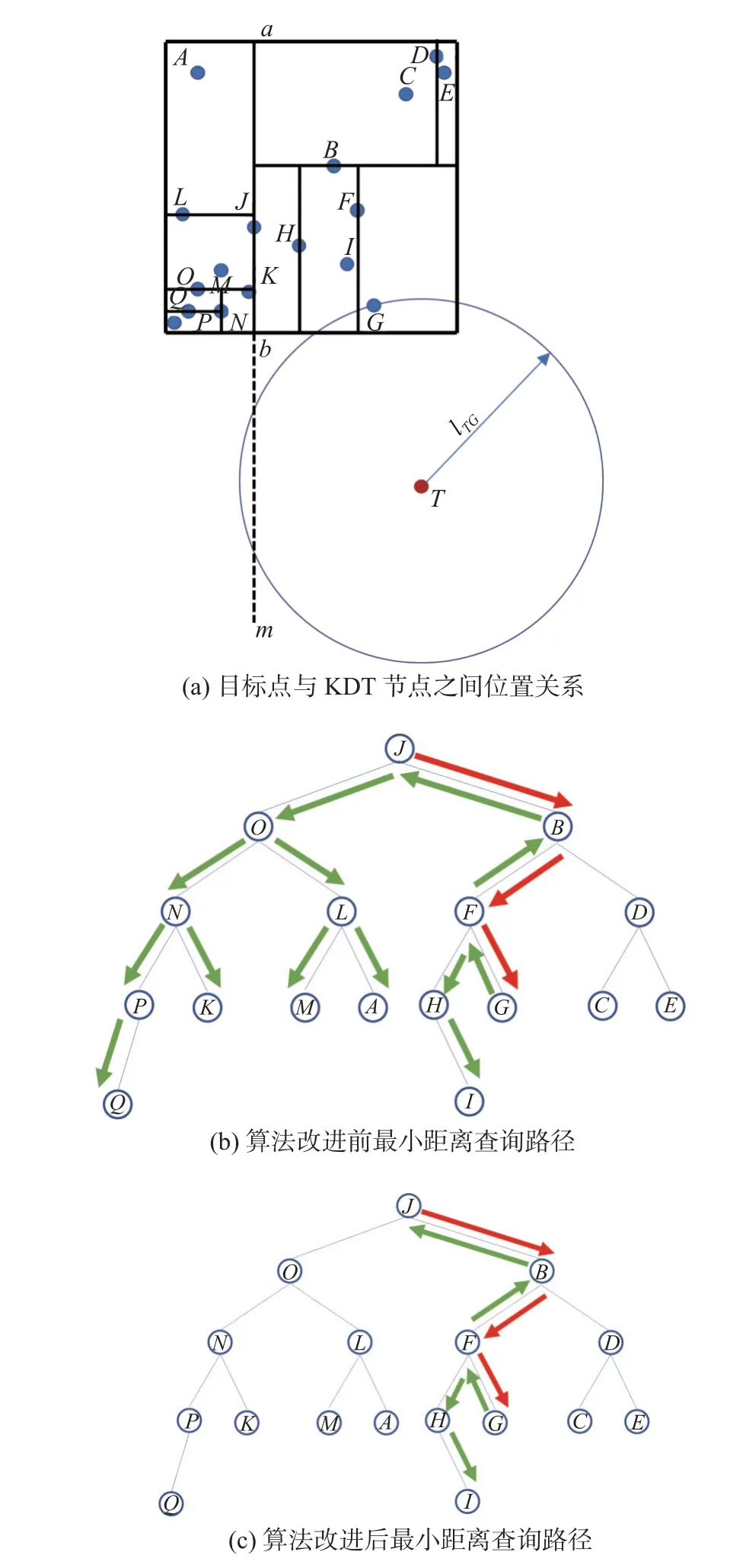
图5 圆与剖分轴相交且回溯无效的情况Fig.5 Sketch of an optimized backtracking process when the circle intersects the split axis

图6 为球、导弹和DPW6 三种几何外形及空间笛卡尔网格。为了定量对比改进前后回溯算法的效率，本文对这三种不同几何外形进行了壁面距离查询测试。对几何外形进行壁面距离查找时，存储所有空间网格点的壁面距离，同时记录得到壁面距离所需的查找次数，然后将查找次数的总和除以空间网格点数得到平均查找次数，结果如图7 所示。从图中可以看出，针对不同外形，本文改进的回溯方法均可有效减小查找次数。针对同一几何外形，物面三角形数量越多，查找次数减少的越明显。

图6 三种几何外形Fig.6 Three geometries

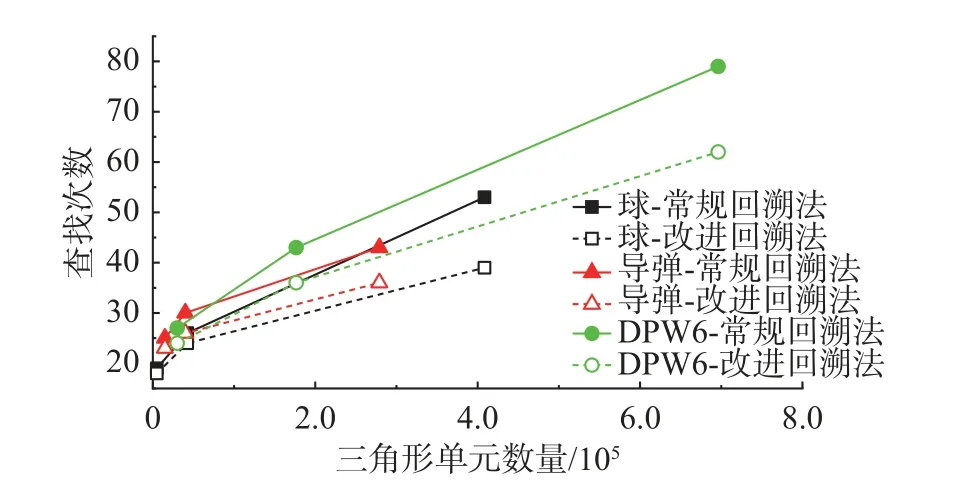
图7 求最小距离所需查找次数Fig.7 Number of queries for finding the minimum distance

4 算例测试

本小节对本文发展的壁面距离算法的准确性和效率进行了测试。测试的几何外形仍为球、导弹和DPW6。为了保证测试结果的合理性，本文所有工况均在AMD EPYC 7702 的处理器上测试，测试平台为Window 10 系统及Visual Studio 2012 版本。每个工况测试10 次，统计平均获得程序运行的时间。

首先对壁面距离结果的准确性进行对比测试。对壁面距离的两种计算方式进行对比，第一种是近似壁面距离，即空间点到物面三角形中心的最小距离，第二种是精确壁面距离，即采用本文发展的算法计算得到的最小距离。计算结果如图8 所示，图8（a）为近似壁面距离计算的结果，图8（b）为精确壁面距离计算所得结果。从图8（a）中可以明显看出，球的近似壁面距离云图及等值线呈现波浪状，与实际物理特征明显不符。采用本文方法计算得出的精确壁面距离等值线光顺平滑，符合物理特征。对于几何外形较为复杂的DPW6，在远离壁面区域，两种计算方法得出的壁面距离结果接近；而在近壁区域，采用近似壁面距离计算方法得到的壁面距离为250 的等值线与实际几何特征误差较大，而精确计算结果的近壁面等值线可较好反映近壁物面特征。

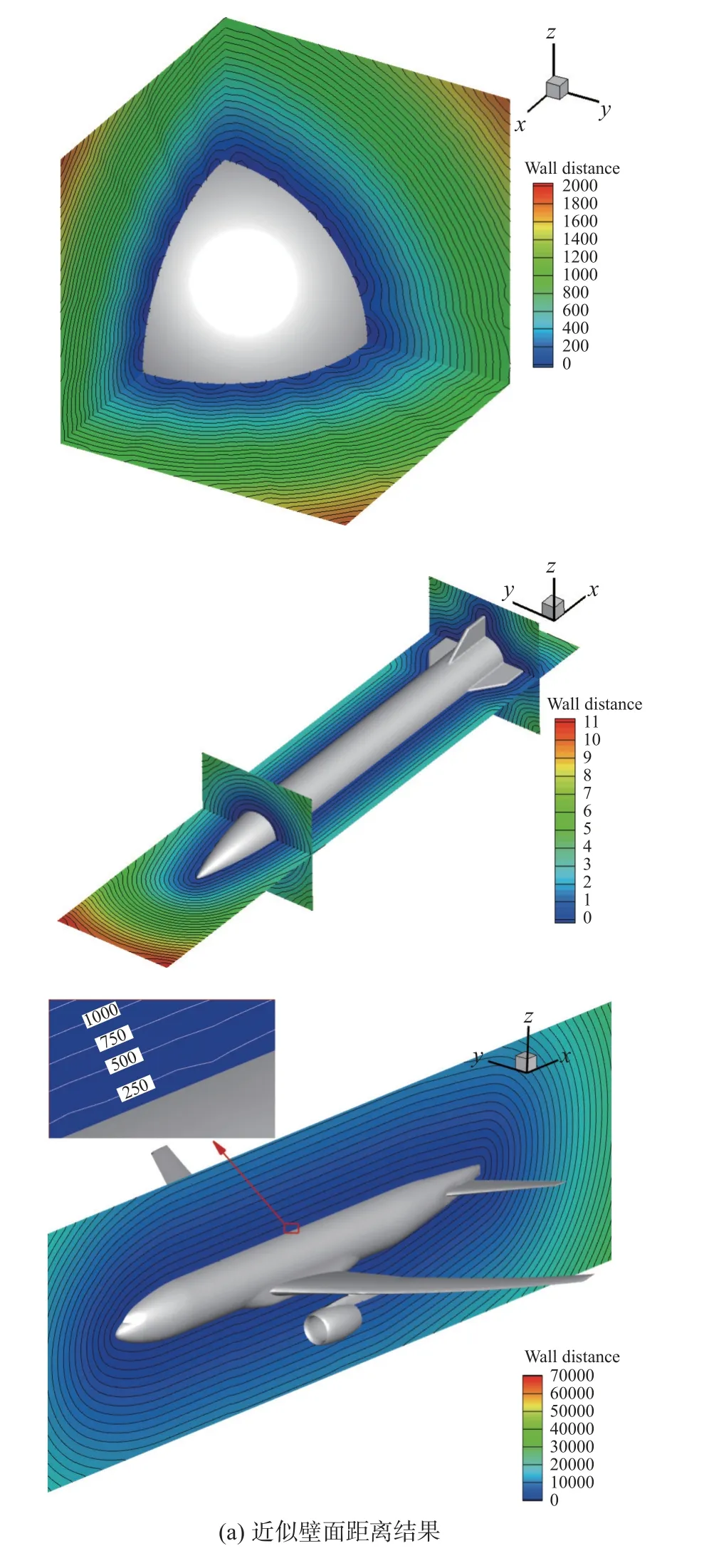
图8 不同几何外形近似壁面距离与精确壁面计算结果云图及等值线Fig.8 Contours of approximate and accurate calculation results for wall distances of different geometric shapes

此外，以球为研究对象，我们将本文方法计算得到的壁面距离与解析解进行对比。结果表明本文方法的计算结果与解析解差异在百万分之一以内。因此，本文方法得到的壁面距离精确性较高。

在计算效率测试方面，对遍历法+精确距离、ADT+精确距离、KDT+精确距离，KDT+近似距离4 种方法的计算效率进行对比。物面三角形数量、空间网格数量以及CPU 运行时间如表1 所示。从表中可以看出，采用KDT 方法的计算效率相比遍历法和ADT 方法均有量级的提升。尤其对于复杂的DPW6 来说，采用遍历法的时间为3 616.87 s，KDT 只需2.92 s，效率提升超过1 000 倍。而对于简单的球来说，效率提升仅不到300 倍。因此，壁面距离查询效率的提升程度与几何外形密切相关。

表1 壁面距离查询所需时间Table 1 Wall-distance querying time

精确距离的计算要比近似距离的计算多调用一个点到三角形距离的函数，此函数在回溯过程中频繁调用会增加计算耗时。从定量结果来看，精确距离计算耗时为近似距离计算耗时的2 倍左右，但这对整个计算周期的耗时影响并不明显。因此，通过增加少量计算时间来获取计算精度收益是值得的。

为了进一步测试本文发展的方法在大规模网格计算时的效率，我们选用DPW6 外形进行物面网格离散并生成空间笛卡尔网格。物面三角形网格数量跨越万、十万以及百万3 个量级；空间笛卡尔网格数量跨越千万、亿以及十亿3 个量级。效率测试结果如表2 所示，结果表明，对于同一种物面离散方式，CPU运行时间与空间网格数量大致呈正比；对于同一数量空间网格（由于物面网格数量不同，加密相同层级生成的空间笛卡尔网格数量有略微差异），物面网格数量从30 021 增加到1 417 181 时，CPU 运行时间仅增加为原来的1～2 倍，这再次说明了本文基于KDT 的回溯方法的高效性。

表2 DPW6 壁面距离计算效率Table 2 Wall-distance calculation time for DPW6

为了与文献[16]中计算效率进行对比，本文选用JSM（JAXA standard model）标模进行壁面距离查询测试，网格规模为33 亿。本文方法（无并行）进行壁面距离查询所需时间大致为0.51 h，文献[16]中采用并行方法对进行壁面距离查询所需时间为0.42 h。因此，除去网格类型、测试环境带来的误差，总体来说，本文方法在大规模网格下仍表现出较高效率。

5 结论

在本文工作中，我们基于笛卡尔网格发展了一种壁面距离计算方法，具备精确性、高效性以及通用性。基于本文内容，主要有以下3 个方面结论：

1）在提高壁面距离计算的准确性方面，我们将物面三角形进行参数化（s和t）表示，根据s和t的取值范围将s-t平面分为7 个区域，对不同区域进行分情况讨论，从而将求最小距离问题巧妙地转化为求约束条件下一维极值问题，计算量大幅减少。

2）在提高计算效率方面，采用平衡的KDT 存储物面三角形所有顶点信息并建立相应的嵌套包围盒，使得在最小距离查询时尽可能快速排除在目标范围之外的单元；同时优化了当前超球面与剖分平面的位置判断法则，解决了在距离物面较远处因无效回溯次数过多导致查询效率下降的问题。

3）此外，本文的壁面距离查询模块是一个单独的模块，在计算壁面距离时，仅需知道空间网格点的位置信息以及物面三角形信息。因此，本文发展的壁面距离计算方法不仅对笛卡尔网格，对结构网格、非结构网格以及重叠网格等也可较好兼容，可方便程序的移植。

本文采用3 个三维几何外形对本文方法进行测试，结果表明计算得到的壁面距离与解析值的误差在百万分之一以内，有较高的精确性；十亿量级网格规模下的单核计算效率与已有文献[16]的并行计算效率相当。虽然在大规模网格测试中表现出较高的计算效率，但仍有提升空间。下一步我们计划添加OpenMP/MPI 并行方法进一步提升计算效率，以满足下一代超大规模CFD 湍流模拟的需求。