8 m×6 m 低速风洞悬臂支撑机构远场干扰试验

刘李涛，黄志远，陈 洪，范利涛，李小兵，刘 砚

(中国空气动力研究与发展中心 低速空气动力研究所，绵阳 621000)

0 引言

风洞试验中，模型支撑装置的存在会对模型表面及其附近流场产生影响（磁悬浮除外），从而对测量的模型气动数据带来干扰[1-2]，有些测量值甚至会严重偏离真实结果。国内外研究者针对风洞试验支撑干扰问题进行了大量的研究，探索出了许多支撑设计优化和工程修正方法，并积累了宝贵的经验[3-12]。

中国空气动力研究与发展中心低速空气动力研究所8 m×6 m 低速风洞（FL-13）主力支撑装置为悬臂支撑机构，运输类飞机模型主要采用基于该机构的斜腹撑形式支撑（如图1 所示）试验，该支撑装置由翼型支杆、直支杆、攻角头、悬臂和双立柱等部分组成。

图1 8 m×6 m 低速风洞悬臂支撑机构Fig.1 The cantilever support device in 8 m×6 m wind tunnel

文献[13]中的DNW-LLF 风洞模型支撑系统与8 m×6 m 低速风洞悬臂支撑机构相似，均存在“悬臂”的特征，基于对该类支撑干扰的物理模型分析，可将其支撑干扰分解为近场干扰和远场干扰。尾流直接作用于模型的支撑干扰一般定义为近场干扰，而尾流不直接作用于模型的支撑干扰一般定义为远场干扰（如图2 所示）。

图2 DNW-LLF 风洞支撑装置近场和远场干扰Fig.2 Near-field and far-field interferences of support device in DNW-LLF wind tunnel

DNW-LLF 风洞支撑干扰的分解是基于气动干扰模型建立的。本文研究过程中，结合8 m×6 m 低速风洞悬臂支撑机构支撑干扰试验方法，对上述支撑干扰分解进行了调整：将可通过支撑干扰试验模拟的翼型支杆、直支杆、攻角头定义为近场支架，将不能（或难以）通过支撑干扰试验模拟的悬臂和双立柱定义为远场支架（如图3 所示）。

图3 8 m×6 m 低速风洞悬臂支撑机构近场和远场支架Fig.3 Near-field and far-field parts of the cantilever support in 8 m×6 m wind tunnel

可见，按照8 m×6 m 低速风洞悬臂支撑机构支撑干扰试验方法，远场干扰量通常难以直接获取，而远场干扰中的悬臂干扰量在某些情况下又不能简单忽略，在一定程度上影响了试验数据准确度，应当对远场悬臂干扰特性进行研究和修正。本文针对悬臂干扰特点，在8 m×6 m 低速风洞采用流场测量和典型模型（主要为CHN-T1 标模[14-16]）测力试验方法进行了研究。

1 悬臂支撑机构远场干扰误差分析

为分析 8 m×6 m 低速风洞悬臂支撑机构远场悬臂干扰的误差，对模型4 种试验状态定义如图4 所示：A 状态为“腹撑”状态（基本试验状态），B1 状态为“背撑+假腹撑”状态，B2 状态为“腹撑+假背撑”状态，C 状态为“背撑”状态。

图4 8 m×6 m 低速风洞悬臂支撑机构试验状态定义Fig.4 State definition of the cantilever support device in 8 m×6 m wind tunnel

本文分别采用两种方法进行“两步法”支撑干扰试验，获取A 状态（腹撑）支撑干扰量：方法一通过B1 状态和C 状态获得，方法二通过B2 状态和C 状态获得，两种方法获取A 状态支撑干扰量的计算公式如下：

其中，F表示气动力量值，ΔF表示气动力差量，下标zj_A表示A 状态支架，下标B1、B2、C 分别表示B1 状态、B2 状态、C 状态。

方法一：B1 状态未模拟腹撑悬臂和双立柱，获得的支撑干扰量可表述为：

方法二：B2 状态未模拟背撑悬臂和双立柱，获得的支撑干扰量可表述为：

可见，方法二相对方法一获得的支撑干扰差量可表述为：

两种支撑干扰试验方法中，攻角头后部断面形成的死水区通常只能小部分模拟悬臂体积效应干扰，同时，当悬臂存在洗流（模型迎角或侧滑角较大，有明显升力或侧力）时，悬臂干扰特性将发生一定变化，导致两种方法获得的支撑干扰量均存在一定不足，实际上，理论腹撑支撑干扰量可表述为：

可见，方法一和方法二获得的支撑干扰量均存在缺项，缺项分别为：

其中，ΔF腹撑悬臂和 ΔF背撑悬臂量值与模型及其部件相对悬臂的位置和距离密切相关，同时还会受到攻角头模拟大小（部分模拟悬臂体积效应）和洗流大小的影响。由于双立柱距离模型区较远，ΔF双立柱一般可忽略。

本文在8 m×6 m 低速风洞对CHN-T1 低平尾布局标模（图5）和某高平尾布局模型采用上述两种方法进行了支撑干扰试验，图6 和图7 给出了腹撑干扰量曲线（未光顺）。其中，“B1-C”和“B2-C”分别表示方法一和方法二获得的支撑干扰量；“Low HT”和“High HT”分别表示低平尾和高平尾布局模型。

图5 CHN-T1 标模支撑干扰试验Fig.5 Support interference test of CHN-T1 standard model

图6 悬臂支撑机构腹撑干扰量曲线（纵向）Fig.6 Aerodynamic interference of the cantilever support (longitudinal)

图7 悬臂支撑机构腹撑干扰量曲线（横航向）Fig.7 Aerodynamic interference of the cantilever support (lateral)

由图6 和图7 可见，相比方法一，方法二获得的升力系数干扰量偏大（低平尾布局偏大约0.035，高平尾布局偏大约0.052），俯仰力矩系数干扰量偏小（低平尾布局偏小约0.058，高平尾布局偏小约0.145）；横向力、偏航力矩、滚转力矩系数干扰量对侧滑角的导数绝对值均有所偏大。

上述结果是由于方法一和方法二获得的支撑干扰量缺项（即悬臂干扰量）不同造成的，可见，8 m×6 m低速风洞悬臂支撑机构的远场悬臂干扰是不能简单忽略的，有必要进行研究和修正。

为对悬臂干扰特性进行定量分析，本文在8 m ×6 m 低速风洞分别采用流场测量试验和典型模型测力试验的方法对悬臂干扰进行研究。

2 悬臂干扰流场测量试验

2.1 流场测量试验内容与方法

悬臂干扰流场测量试验在8 m×6 m 低速风洞无试验模型、保留特大攻角机构远场悬臂和双立柱条件下进行，采用五孔探针测量系统对流场的气流俯仰角和速压进行测量。

五孔探针测量系统包含五孔探针测量耙、测压系统和移测架系统。五孔探针测量耙上安装11 根五孔探针（如图8 所示），探针为半圆球头直圆柱杆，长300 mm，直径8 mm，静压孔距离探头顶端36 mm；相邻探针间距为100 mm，测量耙水平安装于移测架上（即z向测量范围为±500 mm），11 根探针从左至右（逆气流方向看）依次编号为1～11，通过探针上的标准刻线对齐测量耙的水平刻线确保每根五孔探针均无滚转安装角。探针测量的气流俯仰角αq计算公式为：

图8 五孔探针及测量耙Fig.8 Five-hole probe and measuring rake

其中，Cpα=(p下-p上)/(p总-p静)，p上、p下、p总、p静分别表示五孔探针的上孔、下孔、总压孔和静压孔测得的压力值；kα、bα分别表示对五孔探针测量俯仰角标定的斜率和截距。

移测架系统通过电机驱动可沿风洞中心轴线移动，测压系统采用DSM3400 电子扫描阀压力测量系统和1 个量程为5 000 Pa（20 inch H2O）的扫描阀模块，系统测量精度为±0.12%FS。

试验风速为70 m/s，根据8 m×6 m 低速风洞悬臂支撑机构典型支撑位置（如图9 所示）并考虑一定普遍性，试验测量了5 个不同的五孔探针测量耙轴向位置（x原点位于风洞中心，向后为正）下的流场：x1=-1 000 mm（机翼典型轴向位置），x2=-500 mm，x3=0 mm，x4=500 mm，x5=1 000 mm（平尾典型轴向位置）。

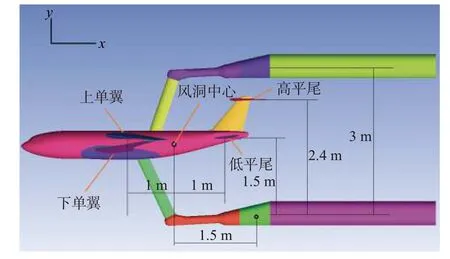
图9 8m×6m 低速风洞悬臂支撑机构典型支撑位置Fig.9 Typical support positions of the cantilever support device

在每个轴向位置，测量了5 个不同悬臂高度下的流场（y原点位于风洞中心，向上为正，由于悬臂距离测量耙过近导致干扰严重，x5未测量悬臂y3高度下的流场）：y1=-2 350 mm（斜腹撑高平尾及较大迎角机翼典型高度），y2=-1 200 mm（斜腹撑机翼及低平尾典型高度），y3=0 mm，y4=900 mm（斜背撑较大迎角机翼典型高度），y5=1 800 mm（斜背撑机翼及低平尾典型高度）。

对于斜腹撑，模型迎角逐渐增大时，模型x向位置逐渐增大（向后移动），悬臂y向位置逐渐减小（向下移动）；对于斜背撑，模型迎角逐渐增大时，模型x向位置逐渐减小（向前移动），悬臂y向位置逐渐减小（向下移动）。

2.2 流场测量试验结果与分析

图10 和图11 分别给出了典型轴向位置不同高度悬臂对流场气流俯仰角和速压影响曲线（未进行光顺，但去除了明显跳点）。

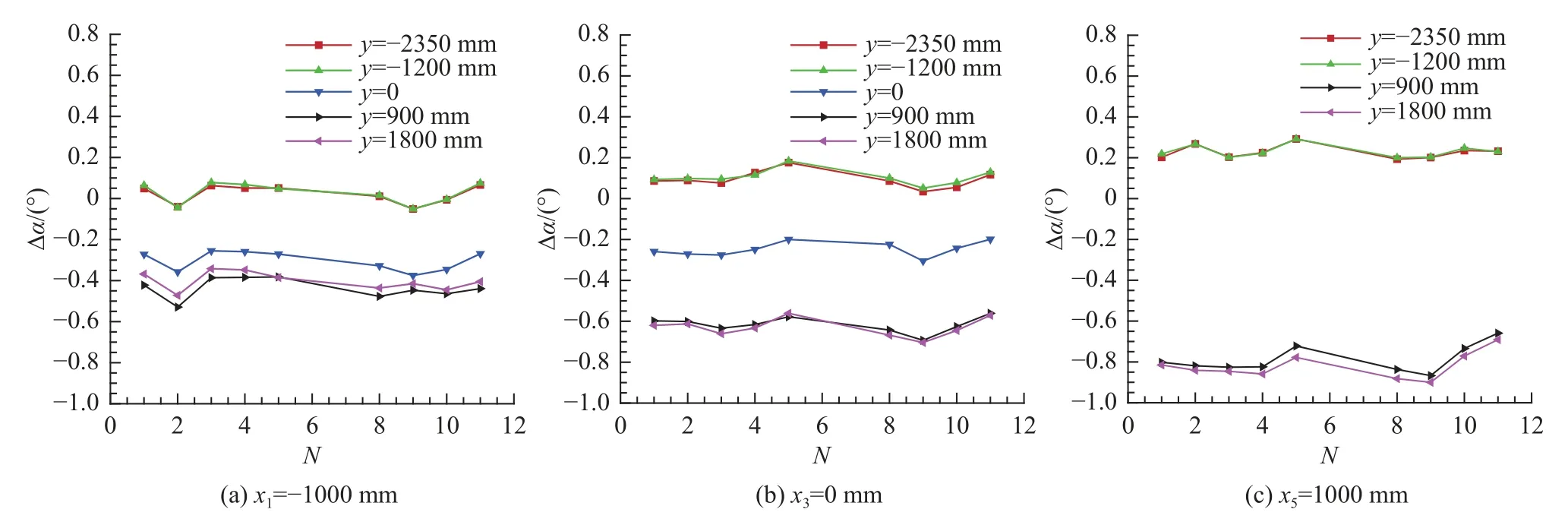
图10 悬臂对气流俯仰角影响曲线Fig.10 Effects of the cantilever support on the flow pitching angle

图11 悬臂对速压影响曲线Fig.11 Effects of the cantilever support on the dynamic pressure

由图10 可见，悬臂高度对风洞气流俯仰角存在一定影响，当悬臂由下向上移动（y由负值逐渐增大至正值）时，风洞中心轴线气流俯仰角由正值逐渐变为负值，悬臂位于风洞中心轴线上方时的气流俯仰角（绝对值）大于悬臂位于风洞中心轴线下方时的值，即背撑悬臂对模型区流场的影响比腹撑悬臂更为严重。

由图11 可见，悬臂高度对风洞速压也存在一定影响，悬臂位于风洞中心轴线时的速压损失较为明显，悬臂位于风洞中心轴线上方时的速压损失大多大于悬臂位于风洞中心轴线下方时的速压损失，同样表明背撑悬臂对模型区流场的影响明显比腹撑悬臂更为严重。

为便于分析，将上述11 根探针测量的流场气流俯仰角和速压增量取平均值，具体量值见表1 和表2。

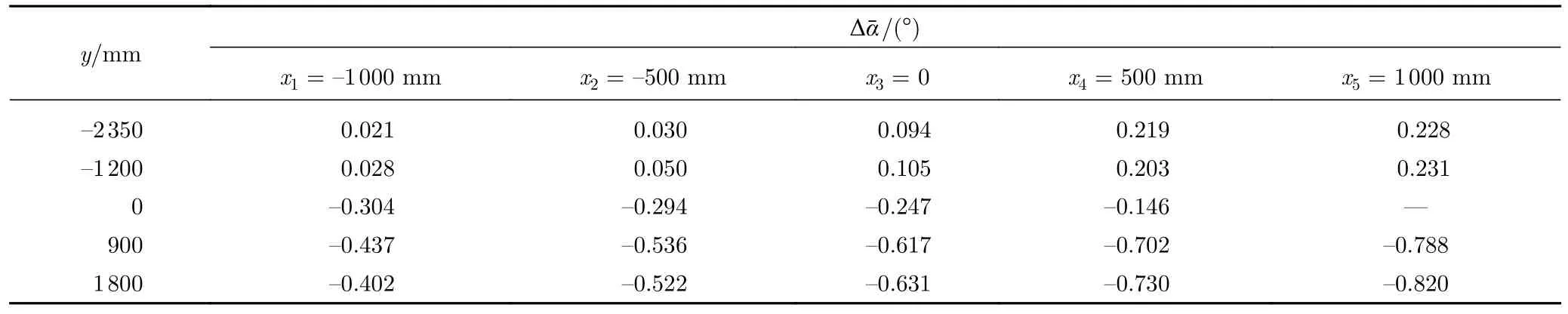
表1 悬臂对气流俯仰角影响量Table 1 Effects of cantilever support on the flow pitching angle

表2 悬臂对速压影响量Table 2 Effects of cantilever support on the dynamic pressure

由图表可见，当悬臂位于风洞中心轴线上方或下方时，风洞中心轴线气流俯仰角的绝对值均随x增大（靠近悬臂）呈增大趋势，且悬臂位于风洞中心轴线上方时的气流俯仰角的绝对值明显大于下方时的值；速压损失随x增大呈先增大后减小趋势，且悬臂位于风洞中心轴线上方时的速压损失大多大于下方时的速压损失；当悬臂正处于风洞中心轴线时，风洞中心轴线气流俯仰角为负值，且随x增大（靠近悬臂）呈绝对值减小趋势，速压损失随x增大急剧增大。造成悬臂位于风洞中心轴线上方和下方明显“不对称”的原因应当是“悬臂”外形的“上下不对称”（由图9可以看出，紧邻攻角头后部的悬臂上方存在明显“斜坡”，而下方较为平坦，并且实际悬臂的上下结构特点存在差异，从而对前方流场形成“不对称”影响）。

3 悬臂干扰模型测力试验

3.1 模型测力试验内容与方法

悬臂干扰模型测力试验在“背撑+假腹撑”（图4 中的B1 状态）基础上进行，腹撑悬臂干扰量通过“有悬臂”状态和“无悬臂”状态（如图12 所示）气动力差量获得：

图12 CHN-T1 标模悬臂干扰测力试验Fig.12 Cantilever interference test of CHN-T1 standard model

悬臂干扰典型模型测力试验中的腹撑假悬臂按照腹撑真悬臂尺寸设计并对其进行一定简化后加工而成。腹撑假悬臂通过三角架固定连接于背撑真悬臂，三角架高度按照模型迎角为0°时的腹撑悬臂位置设计加工（随模型迎角变化，腹撑假悬臂高度存在一定失真：迎角15°时的高度误差为3.5%，约105 mm，由表1 可知，该高度误差影响可忽略）。相比图4 中的B1 状态，试验中的假近场支架不含假攻角头，试验中，由于假悬臂与假近场支架存在相对运动，通过连接于假悬臂且可在一定范围内活动的假攻角头（图12 中未展示）进行过渡。

试验风速为70 m/s，分别对CHN-T1 低平尾布局标模进行了纵向和横航向悬臂干扰试验，对某高平尾布局模型进行了纵向悬臂干扰试验。

3.2 模型测力试验结果与分析

图13 和图14 分别给出了纵向和横航向腹撑悬臂干扰量与近场干扰量对比曲线。其中，“B1-C”表示方法一获得的支撑干扰量（即为腹撑近场干扰量），“Low Beam”表示悬臂干扰试验获得的腹撑悬臂干扰量；“Low HT”和“High HT”分别表示低平尾和高平尾布局模型。

图14 悬臂支撑机构腹撑悬臂干扰量曲线（横航向）Fig.14 Aerodynamic interference of the cantilever support (lateral)

由图13 可见，纵向腹撑悬臂干扰量与近场干扰量相当；由图14 可见，横航向腹撑悬臂干扰量比近场干扰量小1 个量级，基本可以忽略。

4 悬臂干扰修正方法建立与分析

4.1 悬臂干扰修正方法建立

根据运输类飞机模型气动特性和悬臂对其干扰特点，忽略悬臂对模型区速压的影响，同时简化或忽略部分小量，依据流场测量获得的悬臂对模型各部件所在位置气流偏角的影响，可建立运输机类飞机模型试验悬臂干扰修正方法如下：

4.2 悬臂干扰修正方法分析

基于前述悬臂干扰误差分析、悬臂干扰流场测量以及悬臂干扰典型模型测力试验结果，对纵向悬臂干扰修正方法进行分析。

根据图9 所示，对于典型机翼所在位置，可近似取x=-1 000 mm，对应悬臂高度为y=-1 200 mm（腹撑）、y=1 800 mm（背撑）；对于典型低平尾所在位置，可近似取x=1 000 mm，对应悬臂高度为y=-1 200 mm（腹撑）、y=1 800 mm（背撑），对于典型高平尾所在位置，近似取x=1 000 mm，对应悬臂高度为y=-2 350 mm（腹撑）。这些位置速压损失系数在0.006 以下，可忽略其影响。

依据表1 给出的流场测量结果，按典型机翼和平尾处腹撑与背撑悬臂高度下的气流俯仰角差量可估算腹撑悬臂与背撑悬臂升力系数干扰差量，按典型低平尾处腹撑与背撑悬臂高度下的气流俯仰角差量可估算腹撑悬臂与背撑悬臂俯仰力矩系数干扰差量，估算过程及结果详见表3，表4 给出了升力系数和俯仰力矩系数干扰差量流场测量估算结果与图6 给出的悬臂干扰试验结果对比。

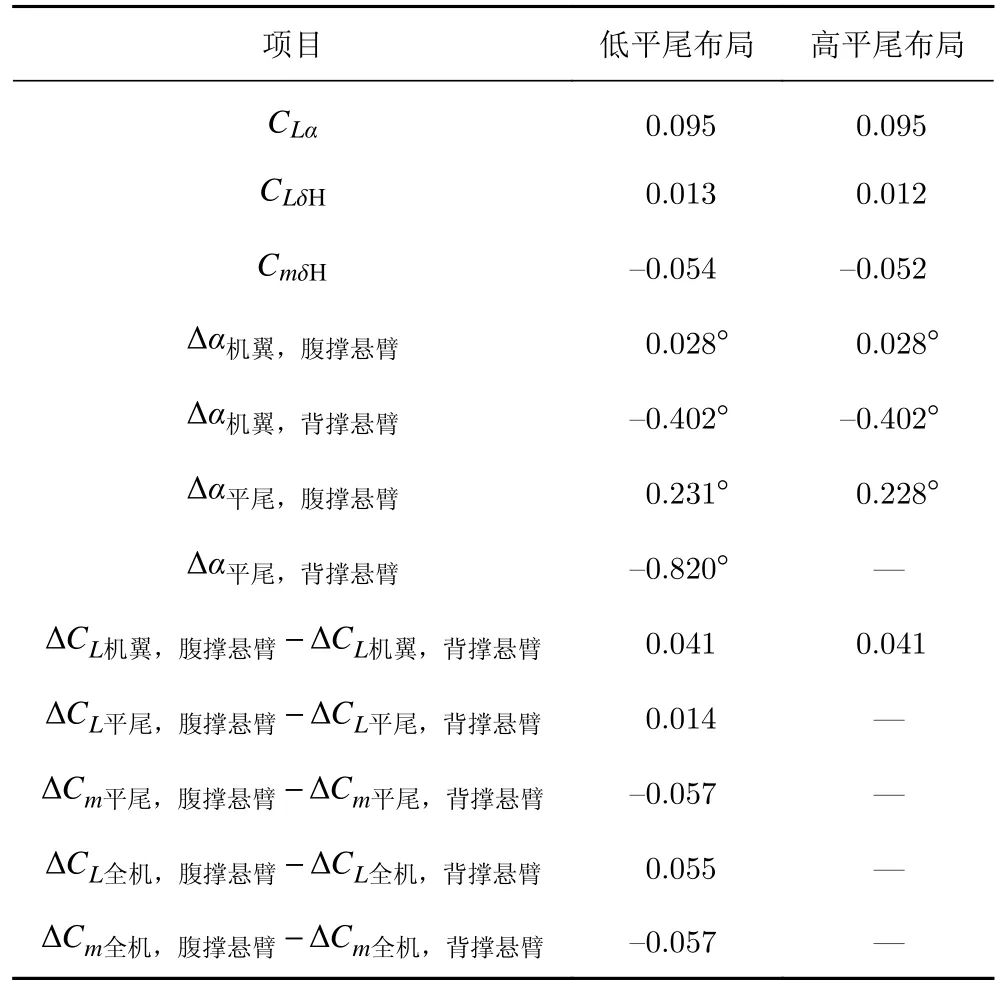
表3 腹撑与背撑悬臂气动干扰差量估算结果Table 3 Difference of aerodynamic interferences between ventral and dorsal cantilever supports

表4 腹撑与背撑悬臂气动干扰差量结果对比（α=0°）Table 4 Comparison of aerodynamic interference between ventral and dorsal cantilever supports (α=0°)

由表4 可见，对低平尾布局，腹撑与背撑悬臂俯仰力矩系数干扰差量流场测量估算结果和支撑干扰试验结果吻合较好，升力系数干扰差量流场测量估算结果量值偏大；对高平尾布局，由于测量位置所限，无法采用流场测量结果进行准确估算，但趋势与低平尾布局一致。分析认为，流场测量估算的升力系数干扰差量结果偏大的原因很可能是机翼所在位置的实际气流俯仰角小于表3 使用的气流俯仰角：本文气流俯仰角测量范围是在z向（展向）±500 mm，而实际机翼展向跨度约为±2 500 mm，该范围内的实际气流俯仰角小于测量范围内的俯仰角是易于理解的。

依据表1 给出的流场测量结果，按典型机翼和平尾处腹撑悬臂高度下的气流俯仰角可估算腹撑悬臂升力系数干扰量，按典型低平尾和高平尾处腹撑悬臂高度下的气流俯仰角可分别估算腹撑悬臂俯仰力矩系数干扰量，估算过程及结果详见表5，表6 给出了流场测量估算结果与悬臂干扰试验结果（取图13 中迎角范围-4°～6°的平均值）对比。

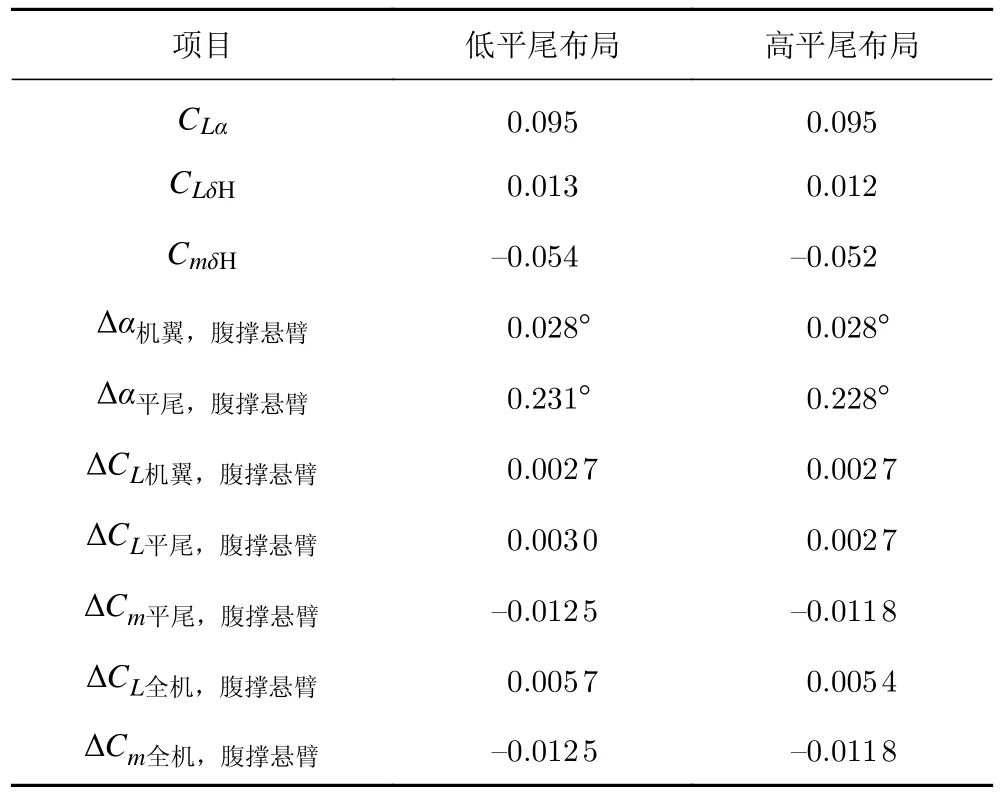
表5 腹撑悬臂气动干扰量估算结果Table 5 Aerodynamic interference of the ventral cantilever support

表6 腹撑悬臂气动干扰量结果对比Table 6 Comparison of aerodynamic interference of the ventral cantilever support obtained by numerical simulations and experiments

由表6 可见，低平尾布局和高平尾布局的腹撑悬臂干扰量流场测量估算结果和悬臂干扰试验结果吻合较好。可见，本文建立的悬臂干扰基本修正方法是可行的，能够用于运输机类飞机模型试验的远场悬臂干扰修正。此外，由表4 和表6 结果对比可以看出，纵向腹撑悬臂干扰量明显小于背撑悬臂干扰量，即在不考虑远场干扰条件下，对运输类飞机布局而言，方法一（采用“背撑+假腹撑”模拟B 状态）作为常规支撑干扰试验方法，获得的支撑干扰量更为可靠。

5 结束语

本文在8 m×6 m 低速风洞采用流场测量试验和典型模型测力试验获得了悬臂支撑机构远场悬臂干扰特性数据并建立了基本修正方法，研究得到：

1）悬臂由下向上移动时，风洞中心轴线气流俯仰角由正值逐渐变为负值，背撑悬臂对模型区流场的影响比腹撑悬臂更为严重。

2）当悬臂位于风洞中心轴线上方或下方时，风洞中心轴线气流俯仰角的绝对值均随x增大（靠近悬臂）呈增大趋势，速压损失随x增大呈先增大后减小趋势；当悬臂正处于风洞中心轴线时，风洞中心轴线气流俯仰角为负值且随x增大（靠近悬臂）呈绝对值减小趋势，速压损失随x增大急剧增大。

3）纵向腹撑悬臂干扰量明显小于背撑悬臂干扰量，横航向腹撑悬臂干扰量基本可以忽略。

4）在不考虑远场干扰条件下，对运输类飞机布局而言，采用“背撑+假腹撑”模拟B 状态作为常规支撑干扰试验方法，获得的支撑干扰量更为可靠。

通过以上研究表明本文建立的悬臂干扰基本修正方法是可行的，能够用于运输机类飞机模型试验的远场悬臂干扰修正。结合本文获得的悬臂干扰特性数据，后续还将在此基础上完善悬臂支撑机构远场干扰通用修正方法，并提供数据支撑。