斜腹板倾角对流线型箱型结构涡振性能影响的数值研究
2023-09-02张亮亮
张亮亮
(山西省交通规划勘察设计院有限公司,山西太原 030032)
0 引言
桥址场地类型、结构气动外形等是影响桥梁结构涡激振动的主要因素,在实际工程中,桥梁主梁断面的形式大小各异。已有许多风洞试验证明结构气动外形细微的变化能导致该结构风振性能发生巨大变化,是影响风致振动的重要因素之一,如虎门大桥由于沿桥跨边护栏设置水马改变了原有结构的气动外形,导致在特定风环境下发生涡振现象[1-2]。王骑[3]等以流线型钢箱梁断面为研究对象进行风洞试验,发现检修车道和栏杆会弱化原有箱梁断面的气动性能,而导流板和风嘴的设置对原有断面的涡振是有利的。胡腾飞[4]等研究了钝体断面列车对斜拉桥涡激振动的影响,发现不能忽视钝体列车对车桥系统涡激振动稳定性的影响。黄林[5]等以π 型叠合梁双塔斜拉桥为研究背景,通过风洞试验发现30°倾角导流板组合措施抑制涡振的效果最佳。文献[6]以淮安大桥为研究对象,在长安大学风洞实验室进行试验研究,观测到+5°风攻角时发生竖向涡激振动现象,本文也以文献[6]的淮安大桥主梁断面为研究对象,通过数值模拟的方法,研究斜腹板倾角对流线型箱型断面涡激振动的影响。
1 数值方法
1.1 流体力学连续性方程
自然界任何流体运动问题都必须要满足流体连续性方程[7]:
式中:μx、μy、μz分别为x、y、z三个方向的速度分量,m/s;t为时间,s;ρ为密度,kg/m3。
1.2 涡振竖向响应简化振动方程
式中:m为结构振动系统总质量;c为结构振动阻尼;k为结构振动系统沿振动方向的刚度;F为t时刻沿振动方向结构所受到的外力总和、yt分别为t时刻的加速度、速度和位移。
1.3 计算模型
涡振竖向响应是桥梁工程中备受关注的一种振动,可将竖向响应计算模型简化成质量-弹簧-阻尼系统,如图1 所示。箱梁断面竖向涡振数值模拟计算模型的背景网格和重叠网格均采用四边形结构网格,整个流场计算域背景网格大小为31B×20B,重叠网格大小为1.5B×2B,计算断面距离上游进口10B,距离下游出口20B,距离上、下边界10B,其中B为箱梁断面的宽度。边界条件[8]:上游来流入口边界设为速度入口;下游出口边界设为压力自由出口,其相对压力值设为0;上、下两侧的边界设为对称边界,垂直该边界方向的速度为0;计算矩形断面的边界为无滑移壁面边界;重叠网格与背景网格的交界设为重叠边界。通过某流体计算软件二次开发外接口自编程序(UDF)来进行流体与详细断面结构间的耦合计算。计算域大小和边界条件设置如图2 所示,计算模型网格划分如图3 所示。
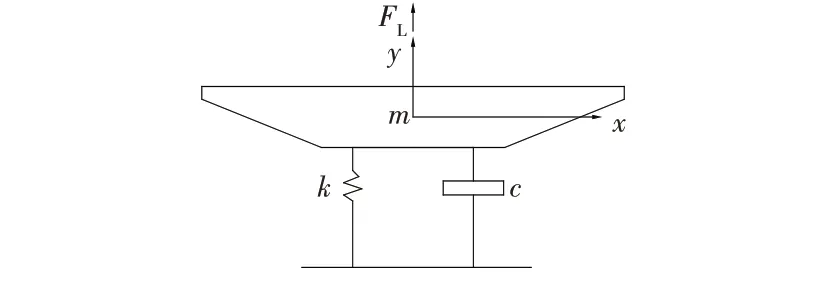
图1 箱梁断面竖向涡振计算简化模型
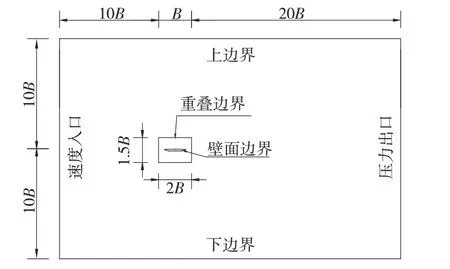
图2 计算域和边界条件

图3 网格划分示意图
1.4 计算工况
为分析斜腹板倾角α对流线型箱型断面涡激振动的影响规律,采取保证主梁顶板宽度B、梁高h、底板宽度b不变,只调整翼板厚度d来改变翼板夹角的方法,如图4 所示。选取了腹板倾角16°~20°五个断面进行涡激振动数值计算,各计算工况断面模型几何尺寸如表1 所示。数值模拟风速为4.5~14.5 m/s,雷诺数范围为1.25×104~6.37×104。
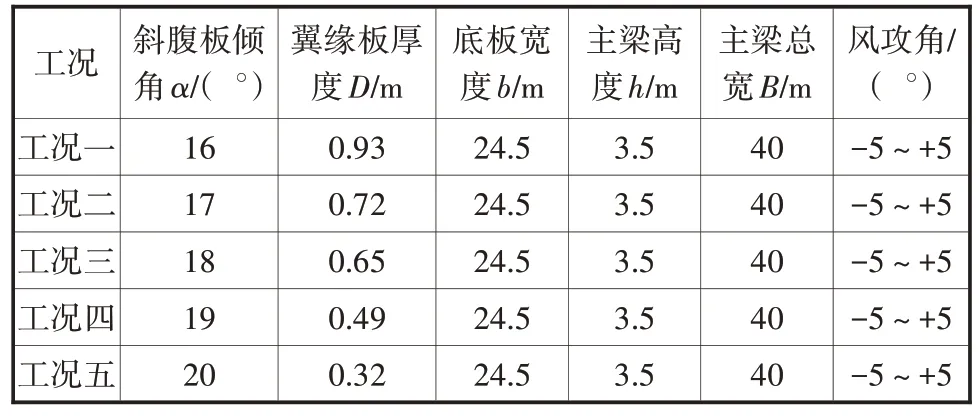
表1 各工况模型尺寸
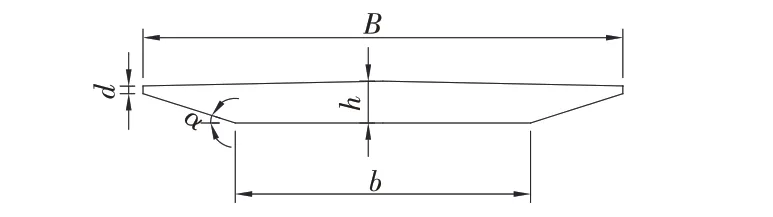
图4 结构断面示意图
2 计算结果分析
图5—图9 分别给出了在+5°、+3°、0°、-3°、-5°风攻角下各斜腹板倾角断面竖向位移比随折减风速的变化情况。纵坐标竖向位移比为竖向振幅ymax与梁高h之比,横坐标为无量纲折减风速。

图6 斜腹板倾角17°时各风攻角下断面位移比随折减风速变化
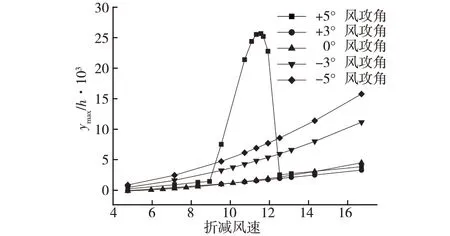
图7 斜腹板倾角18°时各风攻角下断面位移比随折减风速变化
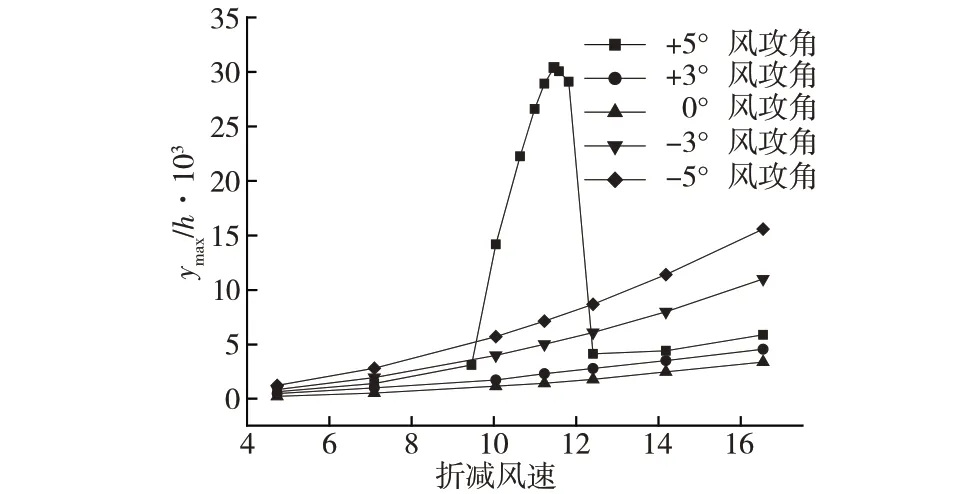
图8 斜腹板倾角19°时各风攻角下断面位移比随折减风速变化
从图中可以看出,斜腹板夹角α为16°、17°、18°、19°、20°、时,风攻角为-5°、-3°、0°及+3°时,模型未有涡激振动现象发生;风攻角为+5°时:
a)工况一 斜腹板夹角α为16°:当风速增加到16.5 m/s 时模型有涡激振动现象发生,并在风速达到18.9 m/s 时涡振振幅出现峰值86.38 mm,最后当风速大于19.5 m/s 时,涡激振动现象逐渐消失,涡振风速锁定区间16.5~19.5 m/s。
b)工况二 斜腹板夹角α为17°:当风速增加到16.5 m/s 时模型有涡激振动现象发生,并在风速达到18.9 m/s 时涡振振幅出现峰值88.34 mm,最后当风速大于20.4 m/s 时,涡激振动现象逐渐消失,涡振风速锁定区间16.50~20.4 m/s。
c)工况三 斜腹板夹角α为18°:当风速增加到15.55 m/s 时模型有涡激振动现象发生,并在风速达到18.9 m/s 时涡振振幅出现峰值91.14 mm,最后当风速大于20.4 m/s 时,涡激振动现象逐渐消失,涡振风速锁定区间15.55~20.4 m/s。
d)工况四 斜腹板夹角α为19°:当风速增加到16.5 m/s 时模型有涡激振动现象发生,并在风速达到18.9 m/s 时涡振振幅出现峰值106.33 mm,最后当风速大于20.4 m/s 时,涡激振动现象逐渐消失,涡振风速锁定区间16.5~20.4 m/s。
e)工况五 斜腹板夹角α为20°:当风速增加到15.55 m/s 时模型有涡激振动现象发生,并在风速达到18.9 m/s 时涡振振幅出现峰值129.32 mm,最后当风速大于20.4 m/s 时,涡激振动现象逐渐消失,涡振风速锁定区间15.55~20.4 m/s。
综上所述,从图中可以得出:在+3°、0°、-3°、-5°风攻角下各腹板倾角主梁断面均未有涡激振动现象发生,即在原流线型箱型断面未发生涡激振动现象的风攻角下,通过调整翼板厚度来改变斜腹板倾角,并不能改变原有断面风致振动状态。在+5°风攻角下各腹板倾角主梁断面均有涡激振动现象发生,各断面发生涡振的风速锁定区间几乎不会随着腹板倾角的改变而改变;但各断面的最大竖向位移比随着腹板倾角的增大而增大;相对于腹板倾角16°的断面,腹板倾角17°断面的最大位移比增大了约2.29%,腹板倾角18°断面的最大位移比增大了约5.48%,腹板倾角19°断面的最大位移比增大了约23.11%,腹板倾角20°断面的最大位移比增大了约49.58%,整体增长趋势大致呈指数型增长。
由图10 和表2 也可以得到,在+5°风攻角下发生涡振时,各断面升力系数也随着斜腹板倾角的增大而指数型增大,侧面验证了流线型箱型断面在发生涡振时,最大竖向振幅会随着斜腹板倾角的增大而指数型增大。

表2 各斜腹板倾角断面+5°风攻角时升力系数均方根CrLms
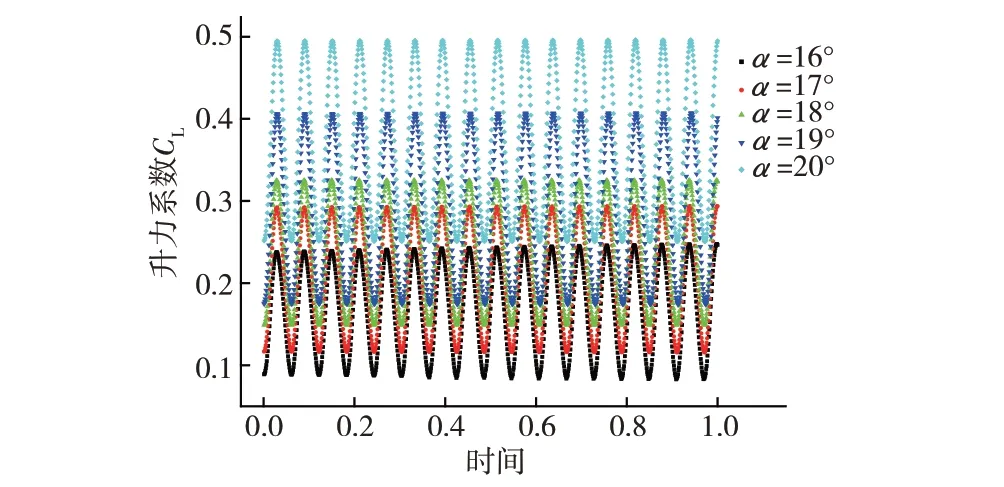
图10 +5°风攻角下各斜腹板倾角振幅最大时升力系数时程曲线
3 结论
通过对流线型箱型断面桥进行数值模拟研究了斜腹板倾角对其涡激振动的影响,主要结论如下:
a)在原流线型箱型断面不发生涡振的风攻角下,其风振状态不会随着斜腹板倾角的改变而发生变化。
b)在原流线型箱型断面发生涡振的风攻角下,涡振风速锁定区间不会随着斜腹板倾角的改变而发生变化,但其最大竖向振幅随着斜腹板倾角的增大而指数型增大。
