把握数学度量本质 促进结构化教学

陈辉玲

（福建省厦门市集美区实验小学）

《义务教育数学课程标准（2022 年版）》（以下通称“新课标”）指出，在教学中要重视对教学内容的整体分析，帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系。结构化教学要求教师站在整体的视角，运用联系的观点对教学对象、学习过程、学生思维进行全面、系统得把握。教师在教学中要形成一个“从宏观到微观”的总体框架，“望”知识的过去、现在和未来，对知识进行结构化；“望”学生动态的学习过程，选择合适的学习策略，对学习过程进行结构化；“望”学生数学思维的发展，高位引导，对数学思维进行结构化。

一、纵向把握度量本质，促进数学知识结构化

面积单位度量教学北师大版数学教材安排在三个不同学年，在二年级上册安排长度的测量，也就是一维图形的度量，本质是长度单位的累加，可以看成是几个长度单位=长度；在五年级上册安排面积的测量，也就是二维图形的度量，本质是面积单位的累加，可以看成“一行里单位面积的个数×行数=面积”；在五年级下册安排立体图形体积的测量，也就是三维图形的度量，本质是体积单位的累加，可以看成“一行里单位体积的个数×行数×层数=体积”。平行四边形面积的计算是二维图形度量的一部分，距离学生学习长方形和正方形面积的计算已经有两年时间，学生对面积度量本质有所遗忘，而平行四边形面积的计算公式的推导又比较抽象，学生要寻得本质进行学习难度较大。教师应立足于面积度量本质进行教学设计，应注重本节课承上启下的作用。在复习过程中，教师应引导学生感受知识的根源与螺旋上升特点，将知识系统化、结构化。

【教学片段1】

1.出示一条线段：你知道这条线段的长度吗？

生：用尺子量一量线段中有几个1 厘米，就是几厘米。

2.出示标有长和宽的长方形：你会算这个图形的面积吗，你是怎么得到这个长方形的面积的？

生：我是用“长×宽”计算出来的。

生：一行有6个1平方分米，4行有24个1平方分米，就是24平方分米。

【设计意图】复习线段的度量和长方形面积的度量，唤醒学生已有的系统知识，为本节课知识的学习做好准备；复习长方形面积计算公式及其度量本质，为平行四边形面积计算推导做好准备。

3.出示练习：瞧，发生了什么事？

巴依老爷正在卖草皮苗（见图1）：“每平方米草皮10 元。以下草皮都是用24 米绳子围成的，价格都是一样的。”阿凡提赶紧阻止说：“等一等，等一等，不要着急着买！”你们知道阿凡提为什么要阻止吗？（虽然都是用24米绳子围成的，但是面积不一样）

图1 巴依老爷卖草皮苗

【设计意图】将知识与现实世界进行关联，遵循学生的年龄特征设置情境，当长方形和平行四边形的面积的对比涉及个人智慧的体现时，学生会以最快的速度调动已有经验解决问题，感受知识对解决真实问题的帮助，激发学习的欲望，化被动学习为主动学习。数据的设计呈现出周长相同，底不变，学生在具体的情境中感受高的不同所带来的面积的变化，将注意力集中到决定面积大小的“高”上，也初步感知平行四边形面积与斜边长短没有关系，促进数学思维的发展。

二、整体把握课程组织，促进数学学习过程结构化

学生的学习是一个动态的过程，在学习过程中形成特定的思考方法、学习策略、探究过程等，就是一种学习过程结构化。通过学习过程结构化，教师可以引导学生在学习过程中进行学习方法的有效迁移，提高学生的数学学习能力。

本节课设计，从情境创设中引导学生“发现问题”：同周长面积不一定相等，那么面积的大小和什么因素有关呢？学生根据已有的知识经验进行大胆猜测，教师设置探究过程，引导学生“验证猜测”以解决问题，最后通过变式练习，引导学生应用知识。这一结构化的学习过程，可以很好地应用到对三角形、梯形面积计算的推导中，甚至应用到相关课型的知识学习上。学生的探究力就在学习过程结构化中得到不断夯实和提升，进一步提高学习能力。

【教学片段2】

猜想验证，探索本质：这些图形的面积一样大吗？（不一样大）这些是同学们的猜测，你能用你的方法揭开巴依老爷的阴谋吗？

探究活动：

1.谁的面积大？

2.要求独立思考后，用自己喜欢的方式，验证自己的想法（教师提供平行四边形、格子图、剪刀）。验证完成后，在小组内交流自己的方案。

生：我用数格子的方法，将合起来能组成一个完整格的小格子进行组合，再数完整格有几格（见图2），加起来是28格，1格代表1平方米，因此是28平方米。

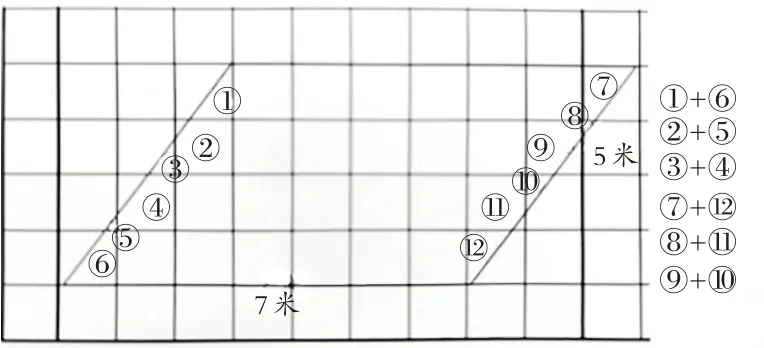
图2 数格子法

生：我把不完整的一小格剪下来拼到另一边，发现刚好拼成一个正方形，剩下的不完整的格子也是一样，就凑成了完整的格子（见图3）。这样就有4行，每行有7格，7×4=28格，是28平方米。

图3 拼接法

生：我直接把左边这个三角形剪下来，平移到右边，我发现所有的格子也都是一整格的了，而且我还发现，图形变成了长方形（见图4）。这样就很好求面积了，用长×宽=长方形面积，也就是4×7=28 平方米。

图4 平移法

师：同学们经过动脑思考，得出了这么多的解题方案。在数的过程中，你们有没有发现什么不变？什么变了？（引导学生感受割补法这种化零为整的转化方法）

生：形状变了，面积不变。

师：最后这种方法，用到了长×宽，为什么不用长×斜边呢？

生：这里剪拼后是一行有7格，一共有4行，并不是5行，不能乘5，否则就没有意义了。

【设计意图】图2 为带格子的平行四边形，教师可以让学生尝试用数格子的方法解决问题，题中并没有交代“不满一格算半格”的规则，能有效规避学生对这种规则的排斥。由于有部分学生也会运用平移的方法，所以在本环节中教师主要是让学生放开思维、充分说理，引导学生发现平移的方法是为了数“完整的格子”，比直接数格子更科学、直观；在操作过程中，学生运用转化的数学思想方法将未知转化成已知，辨析与平行四边形面积大小有关的因素，最终推理出其计算公式。

三、横向把握面积度量本质，促进数学思维结构化

结构化思维指的是能够从多角度对数学问题展开观察、分析，并利用关联性、系统性、整体性的思维找到解题策略，找到解决数学问题的思维方法。

在本节课的教学中，教师可以依托面积度量本质，引导学生横向对比分析不同图形的特征，迁移面积计算推理学习方法，也可以从图形维度角度入手，引导学生发现、总结一维和二维图形面积的度量本质，从而联想到三维图形的度量。通过这样的引导，学生形成结构化的数学思想以及结构化的问题解决策略和方法，也就是形成一种更为上位的结构化思维。

【教学片段3】

师：通过本节课的学习，你觉得你可以解决三角形、梯形的面积计算问题吗？

生：三角形和梯形里也含有不完整的面积单位，与平行四边形面积计算方法相同，先进行切割，转化成长方形或者平行四边形，就可以求出它们的面积了。

【设计意图】方法迁移，感受知识的统一性：转化成底为多少、高为多少，就可以计算有几个这样的面积单位。

师：我们已经学习了一维图形的测量，需要用到长度单位进行累加，又学习了二维图形的测量，将不完整的面积单位转化成完整的面积单位进行累加，那么，同学们还想学习什么知识呢？

生：三维图形的测量，比如长方体的大小测量。

师：你能猜猜如何测量长方体的大小吗？

生：它应该也像长度和面积一样有厘米和平方厘米这样的度量单位，然后看里面有几个这样的度量单位。

【设计意图】在学习完平行四边形面积后，教师引导学生思考，如果以后遇到不同的二维图形应该如何度量，让学生知道求面积就是算有几个这样的面积单位，运用转化的数学思想，将未知转化成已知，进行知识的迁移；再引导学生从一维到二维再到三维图形的度量上思考，感受度量本质知识的一致性，建立起结构化思维。

在教学过程中，教师要重视对教学内容的整体分析，厘清知识体系、对标学习过程策略，引导学生在学习过程中形成结构化思维，让学生能够自信地成为学习主体，有方法、有策略地发现问题，并积极思考探究、解决问题，进而发展学生的核心素养。