基于无监督学习的时序序列故障诊断方法研究
2023-08-31梁秋金王圣杰
梁秋金, 王 铎, 王圣杰, 张 涛*
1. 清华大学, 北京 100084
2. 北京控制工程研究所, 北京 100094
0 引 言
利用无监督学习提取有效的特征表示在机器学习中是一个长期存在的热点问题,无监督学习技术广泛应用于图像分类识别、自然语言处理和目标检测等领域.仅仅利用大量的无标签数据,能够实现将庞杂的数据空间映射到简洁的特征空间,并发掘出隐藏在数据中的隐性特征,并经由迁移学习方法使之能够应用于目标领域,为智能状态辨识等工作提供数据基础[1-5].
在航天领域中,大部分监测数据为时序序列,其基本的故障诊断方法通常为基于传统的数据驱动方法.传统的数据驱动方法在训练模型的阶段中,仅仅利用有标签数据来进行有监督训练,而在实际的大部分故障诊断场景中,故障样本所占的比例远远少于正常样本[5].甚至在某些情况下,需要对设备的运行工况、运行条件与机理具有一定的专业知识才能进行故障的判别与数据标注,这样会带来巨大的人工标注成本.这导致在诊断环境中通常会存在大量的无标签数据,是一个天然的适合开展无监督学习的环境.目前,无监督学习在时序序列故障诊断领域中的研究较少,因此有必要开展基于无监督学习的时序序列故障诊断方法研究,研究如何充分的利用诊断环境中大量的无标签数据进行无监督学习,提取有效的隐性特征并提升诊断效果,从而使得基于数据驱动的故障诊断技术能够进行进一步的大规模应用[6-8].
目前的无监督学习方法一般分为传统无监督学习方法和深度学习无监督学习方法.传统的无监督学习方法主要有聚类(clustering)与降维(demensionality reduction)两大类方法,聚类包括k-均值聚类(k-means)、层次聚类(hierarchical clustering)、DBSCAN等方法,降维包括主成分分析(PCA)、独立成分分析(ICA)等[9-10].
深度学习无监督学习方法主要包括生成式模型和判别式模型两大类,生成式模型主要以自动编码器(autoencoder)、变分自动编码器(variational autoencoder)为主,生成式模型训练的核心思想是提取的特征经过解码器能够重构出原始数据,数据重构的思想与传统的自动编码器并没有区别[6,11-13].但是,能够完成数据重构的特征并不一定是完成下游任务所需要的特征.判别式模型使用类似于有监督学习的目标函数来学习特征的表示,但训练网络所采取的输入数据与标签都来自于无标签数据集,其中基于潜在空间的对比学习(contrastive learning)的判别式方法在图像领域得到了空前的发展,主要思想为学习到的特征要能够与其他样本进行区分[5,14].但其中如何构建合适的正负样本是一个非常棘手的问题,特别是对于非图像数据,对其进行类似于图像的增强变换,可能会失去原始数据的实际意义,达不到提取特征的效果.基于最大化互信息(DIM)的判别式方法主要考虑尽可能最大化特征向量与中间特征图的互信息[15-16],在图像的特征提取中实现了非常好的效果,并避免了正负样本构造的问题,但在时序序列中还暂未展开应用.
基于上述分析,本文主要面向时序序列故障诊断,针对诊断环境中大量无标签数据未被充分利用的问题,提出了一种基于无监督学习的时序序列故障诊断方法,创新点在于:
1)通过改进最大化互信息这一判别式方法,对时序序列数据进行局部互信息估算时的损失函数进行了优化;
2)针对无监督训练的损失函数,对超参数的选取进行了探索,并选取了最适合时序序列故障诊断的目标函数;
3)优化其固定的模型训练模式,采用自适应的训练过程,构建了具有稳定收敛性的无监督特征提取模型.
该方法首先在公开的凯斯西储大学轴承数据集[15]进行了验证,在不同工况下,基于该诊断方法的故障诊断精度远远高于基于自动编码器的故障诊断方法,精度均在95%以上;在该无监督特征提取模型的基础上采用KNN与SVM方法进行故障诊断,平均诊断精度达到了95%以上,远远高于直接在原始数据空间中进行诊断的精度;最后,我们在卫星监测时序数据上进行了验证,采用可视化方法表明了该无监督模型能够很好的捕捉不同故障阶段的数据特性,进一步在实际应用中证明了该无监督模型在时序序列故障诊断中的有效性.
1 基于最大化互信息的判别式无监督学习方法
信息论认为,有效的编码器应该尽可能最小化输入到特征向量之间的互信息,而解码器应该尽可能最大化特征向量与输出之间的互信息,根据这一思想,近些年许多研究人员思考从互信息入手进行特征提取的方法.互信息是信息论中一种有用的信息度量,它可以看成是一个随机变量中包含的关于另一个随机变量的信息量,或者说是一个随机变量由于另一个随机变量而减少的不肯定性.随机变量X与Y的互信息表示如下:
(1)
Donsker和Varadhan给出了互信息的下界,即基于KL散度的Donsker-Varadhan表示
(2)
但互信息的计算一直以来是一个非常困难的问题,因为计算互信息需要同时计算联合分布和边缘分布,因此精确估计互信息的大小是一个非常重要的问题.文献[15]中提出了利用神经网络进行互信息估算的方法MINE(mutual Information neural estimation),其基于KL散度的Donsker-Varadhan表示给出了互信息的下限,公式如下:

(3)
其中对互信息估算的理论推导,首先需要引入称为f散度,定义如下:
(4)
互信息与KL散度之间的关系不难推导,现给出如下公式:
=DKL(PXYPXPY)
(5)
可以看出,互信息的本质含义就是两个变量的联合分布与两个变量的边缘分布之积的KL散度.利用凸函数的性质,容易证明f函数为凸函数,而对于任意一个凸函数,总存在一个凸共轭函数可以对其进行线性近似[14].假设凸函数f(u)的定义域为,对于任意一点ξ,y=f(u)在u=ξ处的切线为
y=f(ξ)+f′(ξ)(u-ξ)
(6)
原函数与该切线函数的差函数为
h(u)=f(u)-f(ξ)-f′(ξ)(u-ξ)
(7)
对于凸函数f(u),下式恒成立
f(u)-f(ξ)-f′(ξ)(u-ξ)≥0
(8)
进一步变换成
f(u)≥f(ξ)-f′(ξ)ξ+f′(ξ)u
(9)
由于可以取等,因此可进一步推导为
记t=f′(ξ),并令
G(t)=-f(ξ)+f′(ξ)ξ
得到凸函数f(u)的估计式
(10)
由于对于每个给定的u值,均需遍历整个f′()寻求使得式(10)取得最大值的t,因此可以认为t为u的函数,即t=T(u),式(10)变换为
(11)
基于式(11)得到如下:
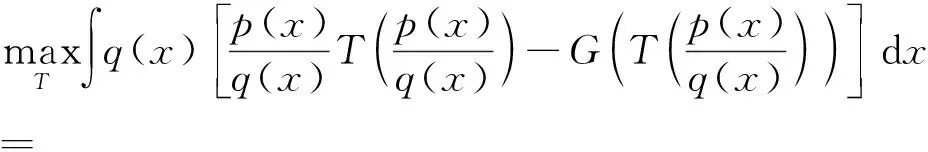
(12)
式(12)即为估算f散度的基本表达式,其基本思路为采用神经网络对T(x)进行拟合,优化其参数,不断扩大分别从p(x)分布与q(x)分布中进行采样的平均值的差,最终结果即为f散度的估计值.
以上完成了对互信息的估算,现在考虑如何对互信息估算结果进行最大化处理.编码前后X与Z的互信息表达式如下:
I(X,Z)=KL(p(z,x)p(z)p(x))=KL(p(z|x)p(x)p(z)p(x))
(13)
目标函数即为最大化互信息的负值
(14)
而KL散度并不存在上界,如果直接利用神经网络去拟合T(x)进行式(14)的最大值求解,可能会得到无穷大的值,结果并不收敛.因此,我们采取JS散度(15)进行估计,JS散度属于之前讨论的f散度,同样可以使用式(12)进行估计计算.
(15)
其中P与Q的值为
P=p(z|x)p(x),Q=p(z)p(x)
(16)
根据JS散度对应的凸共轭函数G(x),式(14)可以得到其对应的估计结果如下所示:
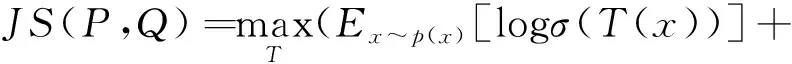
(17)

(18)
文献[16]针对图像领域给出了全局最大化互信息的基本思路,首先将原始图像经过卷积层输出的特征图(一般为M×M块)作为P(x)分布,而经过编码器的最终输出向量y作为P(z)分布,将同一张图像的特征图与特征向量作为联合分布P(z|x)P(x),另一张图像的特征图与该特征向量作为边缘分布乘积P(z)P(x),之后引入判别网络σ(T(x,z))最大化似然函数.本文采用如下的思路进行模型搭建:首先将原始数据进行第一部分编码得到原始特征图,根据原始特征图进行第二部分编码得到特征向量,这两者即为联合分布p(z|x)p(z);将原始特征图的第一维最后一层数据调换至第一层,得到类似随机抽取的特征图,与特征向量组合即为边缘分布p(z)p(x).图1中上面部分为全局互信息估算,原始特征图、打乱的特征图分别与特征向量构造正负样本对,直接进行互信息估算; 下面部分为局部互信息估算,原始特征图、打乱的特征图分别与扩充的特征向量构造正负样本对,将计算得到的局部互信息分数进行平均得到互信息值.
在魏国,李悝主持了政治改革,他坚决反对奴隶主贵族的宗法世袭制度,建立了“食有劳而禄有功”的任官制度,主张“夺淫民之禄,以来四方之士”[16]P166,即剥夺奴隶主世袭的爵禄权力,把这些爵禄转而赐给有那些军功的人。“是时,李悝为魏文侯作尽地力之教”[17]P1124与李悝改革中提出的“尽地力之教”的经济政策相辅相成,大力发展农业生产,提高土地产量。通过这次改革发展了了新兴地主阶级的势力,促进了封建社会的发展。
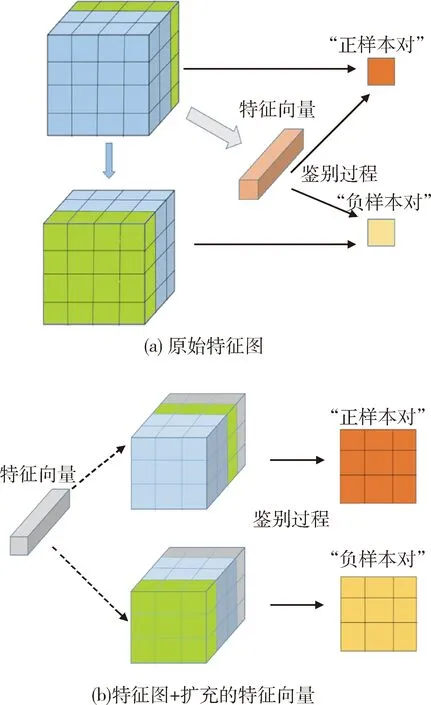
图1 互信息估算示意图Fig.1 Schematic diagram of mutual information estimation
上述目标函数(7)可用于最大化输入和输出之间的互信息,但根据下游任务的不同,这样的方法可能是不可取的.例如,如果要对图像进行分类,就没有必要对像素局部的琐碎噪声进行编码,这样的编码对最终提取的特征并没有任何好处.由于全局最大化互信息会使得输出特征向量与特征图整个部分具有高互信息,因此编码器会选择输入中传递给编码器的信息类型,比如特定于局部部分或者像素的噪声.然而,如果编码器只选择了输入的部分类型数据,那么编码器并没有起到提升最终提取的特征向量与不包含上述噪声的区域部分数据的互信息的作用,这样可能会导致特征图中的有效的、独特的信息被忽略.因此,模型应该考虑到编码特征向量与整个输入局部之间的互信息的计算.可以采取分别将M×M块特征图与编码特征向量进行互信息的计算,具体计算方法如下:
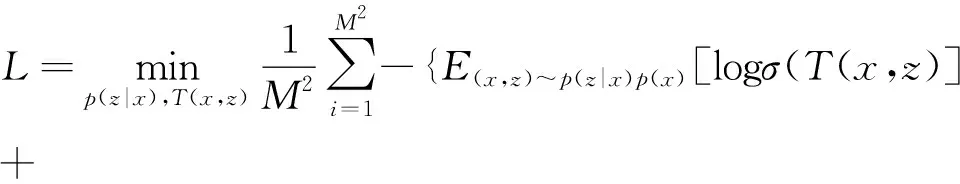
(19)
如果为了获得适合分类任务的表示模型,需要对图像的最终特征表示与特征图局部信息之间进行平均互信息的求取,文献[16]的结果表明这种方法对于下游任务为分类任务的情形是非常有效的.联合分布与边缘分布的构造为将特征向量在维度上扩充至与特征图相同大小,并在第一个维度上进行拼接,最后得到每一个局部分块的分数值.具体过程如图1所示.
以上为最大化互信息判别式方法的主要损失函数与模型介绍,该方法主要是针对于图像领域,对整个特征提取过程中的特征图与特征向量进行互信息的计算,其中包括全局与局部损失函数,基于此训练得到特征提取模型.但是,面对故障诊断中的时序序列数据,该模型仍存在以下几个问题:
1)原模型针对的是二维图像数据,对于时序序列数据,模型结构需要进行调整修改;
2)原模型的最终损失函数是对全局和局部损失函数采取了适合图像的最优比例进行融合,但对于时序序列数据,损失函数的选取仍需要进行实验探索;
3)原模型的损失函数基于多重嵌套优化,而且有全局与局部的参与,训练过程经常出现收敛不稳定的情况,因此需要针对故障诊断的时序序列数据提出合适的训练方式.
2 基于改进最大化互信息的时序序列故障诊断模型
在图像领域,基于最大化互信息(DIM)的无监督特征提取模型在分类、回归等任务取得了很好的实验效果[16],但是在时序序列故障诊断任务上,仍存在一些问题需要进行改进.对DIM时序模型在模型结构、优化的损失函数以及训练方式层面做出改进,以使其适配时序序列故障诊断任务,提高诊断精度.整体的故障诊断模型主要由两部分组成,1)首先进行无监督训练,构建编码器,目标函数为基于最大化互信息的损失函数,利用原始数据中的无标签数据进行训练,当损失函数值减小到低于设置阈值或者迭代次数到达规定次数时该阶段训练完成,得到特征提取模型.模型整体训练流程如图2所示,其中的卷积层采用的是匹配时序数据的一维卷积网络.2)针对分类层进行有监督训练,目标函数为交叉熵损失函数.首先,原始数据中的有标签数据经过1)阶段中训练完成的特征提取器,得到特征向量.其次,在特征空间中,将特征向量输入分类器得到预测分类结果,计算损失函数,利用反向梯度计算进行训练,当损失函数值减小到低于设定阈值或者迭代次数到达规定次数时该阶段训练完成.训练得到的特征提取环节与分类层进行具体的故障诊断.将原始数据中的待标签数据作为输入,经过特征提取器与分类层得到诊断结果,具体流程如图3所示.

图2 无监督模型示意图Fig.2 Schematic diagram of unsupervised training
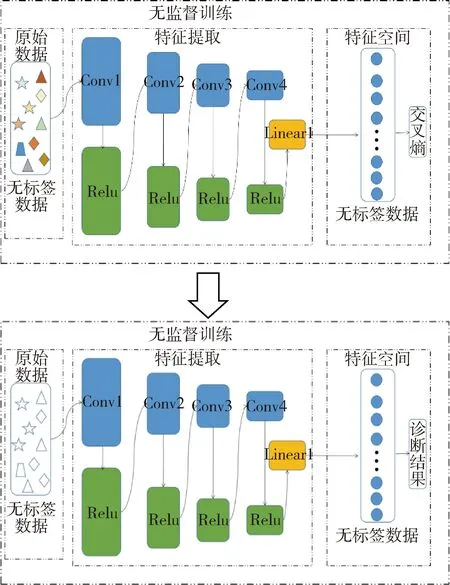
图3 故障诊断模型示意图Fig.3 Schematic diagram of the fault diagnosis model
其中步骤(2)中的有监督训练包括两种形式:第一种为仅进行有监督训练分类层,即不对特征提取器进行梯度计算、累加与网络参数更新,仅对分类层进行参数更新,称为最后微调;第二种为全局有监督训练,不仅对分类层进行网络参数更新,也包括对特征提取器进行梯度计算与网络参数更新以对其进行修正,称为全局微调.无监督训练部分架构的详细信息如表1所示。
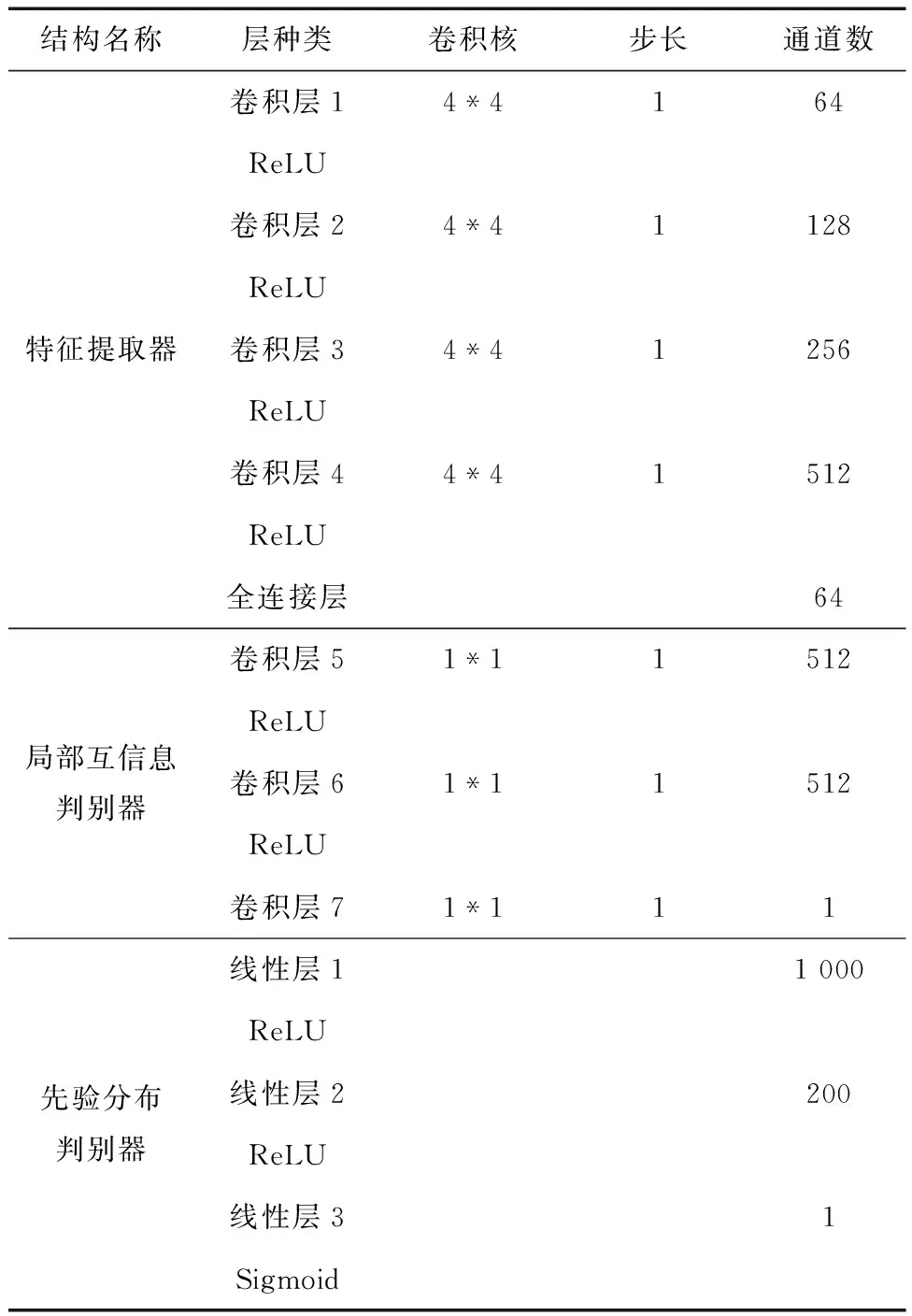
表1 无监督训练架构详细信息Tab.1 Unsupervised training schema details
整体的无监督目标损失函数如式(20)所示,由两部分组成,分别为全局互信息估算、局部互信息估算以及基于先验分布的目标函数,三者通过α、β、γ三个超参数组成整体损失函数.
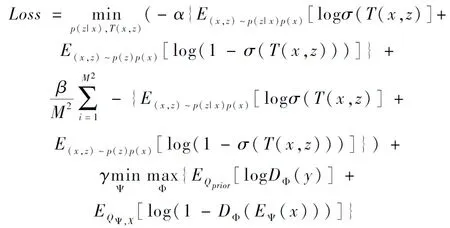
(20)
考虑到时序序列故障诊断的特性,主要在以下部分进行改进:
1)对于无监督训练神经网络,对其原本针对图像的卷积网络进行了修改,采用了适用于提取时序序列数据特征的一维卷积网络,并对时序序列数据进行局部互信息估算时设计了合适的损失函数;
2)对于无监督训练的损失函数,对超参数的选取进行探索,并在实验仿真结果与分析这一章进行详细的分析,最终选取了最适合时序序列故障诊断的目标函数;
3)在无监督的训练方式上,采用自适应的训练过程,在训练前100epochs仅使用全局互信息作为目标函数进行训练,之后采用超参数构成的完整损失函数作为目标函数,构建具有稳定收敛性的无监督特征提取模型.
无监督训练的具体算法如下所示:

算法1 无监督训练/*Algorithm Unsupervised Learning输入:原始空间无标签数据XM,训练迭代次数n1,学习率α1输出:fFE(.)的最优参数θ*FE步骤1: 初始化fFE(.)、flocal(.)和fprior(.)的参数初值:θoFE、θolocal和θoprior步骤2: 分批输入无标签数据XMk∈XM,计算前向传播结果,Losslocal为式(8)中的第二部分,Lossprior为式(8)中的第三部分:Lossilocal=flocal(FiM,Fi)、Lossiprior=fprior(Fi)Lossi1=Lossilocal+Lossiprior步骤3:执行参数更新(前100epochs仅执行全局互信息估算的参数更新),θi+1FE,θi+1local,θi+1prior←θiFE,θilocal,θiprior-α1Δθ Lossi1(XM) STEP4:重复STEP2、STEP3,i=1,2,3…n1
3 实验仿真结果与分析
3.1 数据处理
实验1采用凯斯西储大学(CWRU)轴承中心提供的轴承数据集[20],实验平台包括电机、加速度计和转矩传感器,如图4所示.故障是人为采用电火花加工技术在轴承上布置,数据集为固定在电机外壳上的加速度计所采集得到.在轴承数据集中共有10个类别,分别为3个故障位置(轴承外圈、轴承滚珠和轴承内圈)对应3个不同的故障大小(0.007 in、0.014 in和0.021 in)共9个故障类别与一个正常类别.如图5所示,依次分别为滚珠故障、外圈故障、正常轴承和内圈故障的实物示例.所有数据在4个不同负载的情况下进行收集,共Load0到Load3 4类数据,采样频率设置为12 khz,其中每个类别有500个样本,每个样本为2 048个点的振动信号.本文在实验过程中为了增加故障诊断的难度,仅采用前1 024个点的振动信号,即原始数据为1 024维的数据.图6为不同故障位置对应的不同故障大小与正常数据的共10种样本示例.

图4 CWRU测试台[14]Fig.4 CWRU test bench

图5 4种不同故障状态的轴承[14]Fig.5 Bearings with four different fault states
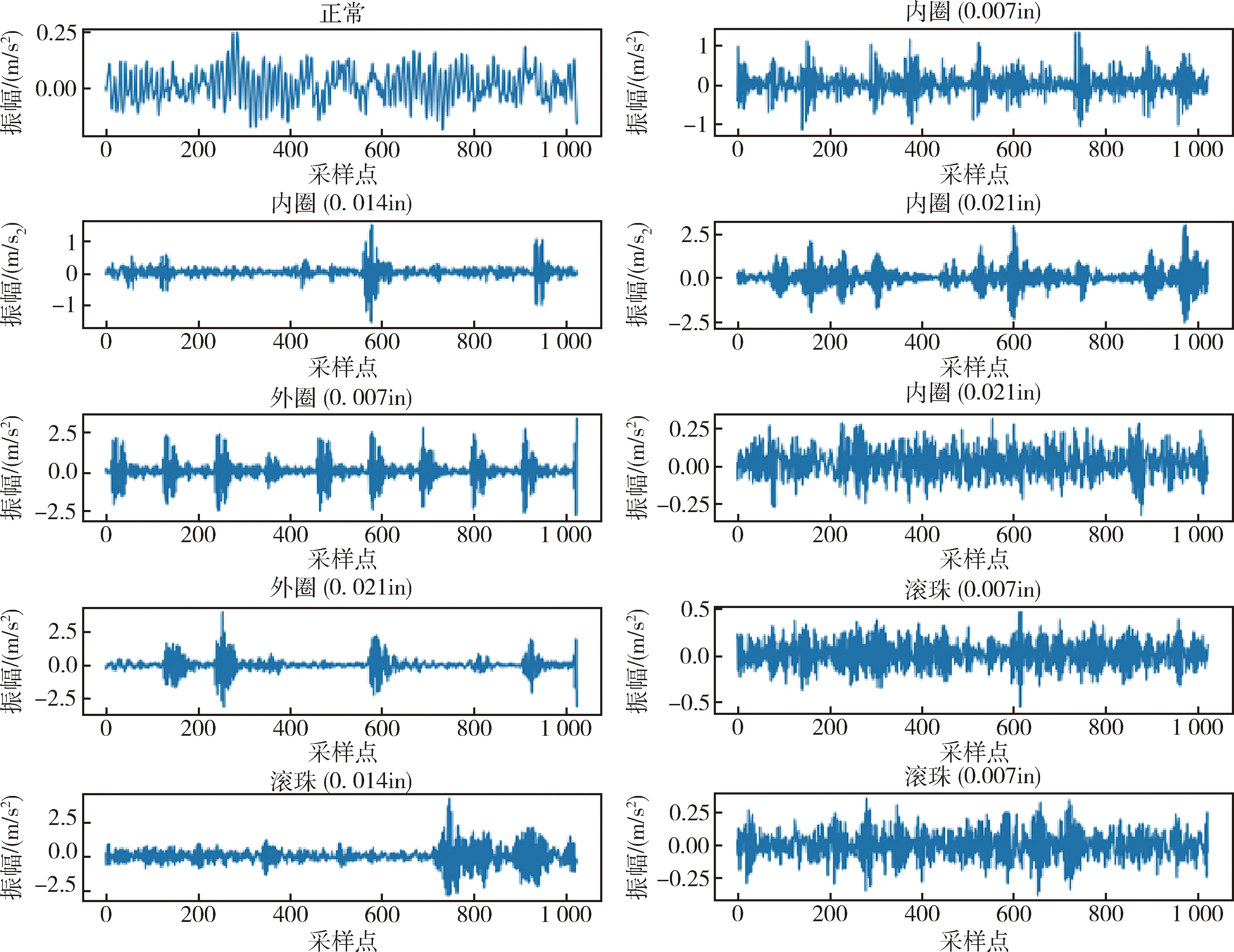
图6 10种故障样本示意图Fig.6 Schematic diagram of ten fault samples
实验2采用的数据为某卫星监测到的电流信号数据,原始数据为长时序列数据,包括了正常运行阶段与故障阶段.该数据存在缺失、毛刺等问题,首先将原始数据进行了插值、平滑等预处理,之后在时间维度上进行了降采样操作,每个阶段随机采样若干个子序列样本,每个样本的序列长度为360,70%的样本用于训练,剩下30%的样本用于测试.
3.2 模型训练
使用Adam优化器来训练所有模型,对于特征提取器的无监督训练,设置超参数β=1,γ=0.1,设置学习率为α1=0.000 1,每批次大小为batch_size1=128,训练迭代次数为200.对于分类层的训练,设置学习率为α2=0.000 1,每批次大小为batch_size2=128,训练迭代次数为epochs2=100.所有实验均在含一台Nvidia Titan RTX GPU、一台Intel Core i9-10980XE 3.00 GHz CPU和128 GB内存的计算机上进行.实验设置的详细列表见表2.

表2 具体实验设置Tab.2 Specific experimental settings
此外,对超参数α与β进行了对比实验,超参数α为全局互信息目标函数的权值,超参数β为局部互信息目标函数的权值.为了对不同的超参数进行合理的比较,进行如下的实验设置:1)始终令α+β=1;2)γ=0.1保持不变.具体实验设置如表3~4所示.

表3 超参数实验设置Tab.3 Hyperparameter experiment setup
3.3 实验结果与分析
主要做了两方面的实验仿真对模型方法进行验证,实验安排如下:
1)采用3.1中介绍的凯斯西储大学轴承数据集,做故障诊断实验,采用故障诊断识别精度作为模型衡量标准,并与自动编码器、KNN和SVM等方法进行对比[11-12].
2)利用某卫星的监测数据,对无监督模型进行验证,进行t-SNE可视化实验,验证特征提取模型的有效性.基于t-SNE算法的数据降维可视化方法其思想是降维前后数据间的关联性应保持不变,将数据关联性通过样本间相似性并进行归一化转换为概率分布模型,通过最小化降维前后数据关联性概率模型的KL散度求解降维特征.将原始高维特征降到2维或3维便可进行可视化.
3.3.1 凯斯西储大学轴承数据集实验
为了保证实验的准确性与评价各种方法的公平性,做出如下数据安排.对于每一个负载情况下的实验,关于DIM-FD与AE-FD训练与测试的数据安排如下:1)特征提取器的无监督训练使用4 000个无标签数据;2)分类层的有监督训练使用1 000个有标签数据;3)故障诊断测试使用1 000个待标签数据.直接Knn方法与直接SVM方法均使用1 000个原始数据进行训练,之后使用1 000个原始数据进行故障诊断测试.特征Knn方法与特征SVM方法均使用在DIM-FD模型中已经训练好的特征提取器进行特征的提取,使用1 000个有标签特征向量进行训练,之后使用1 000个无标签特征向量进行故障诊断测试.
在4种不同工况下的实验结果如表4所示,可以从结果中分析出以下几点结论:1)在4种工况下,DIM-FD(最后微调)与DIM-FD(全局微调)的故障诊断精度均远远高于AE-FD(最后微调)与AE-FD(全局微调)的精度;2)DIM-FD(全局微调)的精度均接近100%.这表明DIM-FD模型构建的特征空间远远优于传统的自动编码器构建的特征空间,在下游故障诊断任务中发挥了更好的作用.
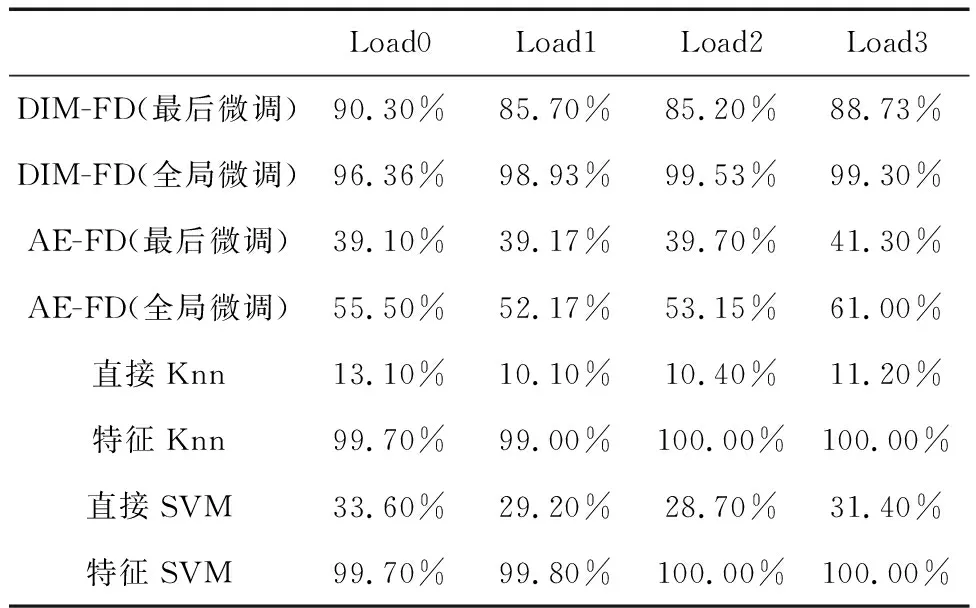
表4 不同工况下不同方法故障诊断精度Tab.4 Fault diagnosis accuracy of different methods under different working conditions
其次,在4种工况下,在原始数据空间进行Knn方法与SVM方法进行故障诊断的诊断精度均远远低于在特征空间下进行相同方法故障诊断的精度,如图7所示.其中,在该数据集中直接用SVM方法进行故障诊断的精度不足40%,直接用Knn方法进行故障诊断的精度甚至不足20%,这反映了该数据集的原始数据空间中数据具有高维、多噪声等缺点,因此导致直接采用基线方法进行故障诊断的效果并不理想.而在基于DIM-FD的特征空间中使用Knn与SVM方法进行故障诊断,均达到了很好的效果,平均诊断精度达到了99.5%以上,其中在Load2与Load3两种工况下,特征Knn方法与特征SVM方法诊断精度甚至达到了100%.这进一步证明了本文提出的DIM-FD方法在故障诊断中的良好性能.

图7 诊断精度对比图Fig.7 Diagnostic accuracy comparison chart
以工况Load0为例,设置不同超参数值的5个分组实验结果如图8所示.结果表明,随着β不断减小、α值不断增加,会使得目标函数中局部互信息所占的比例减小,对于故障诊断这样的分类任务而言编码器的效果越差.当设置β=1、α=0时,编码器特征提取的效果达到最佳,故障诊断率达到最高.进一步证明了,使用全局互信息的估计可能会选择输入的部分信息通过编码器,例如含有噪声的局部,这样不会增加与其他无噪声的局部互信息,导致部分有效的信息未被编码器进行特征提取.而对于故障诊断这类分类任务来说,一些无用的噪声数据对其是没有任何帮助的,所以编码器应当以最大化局部互信息为目标函数才能使得编码的效果达到最好.

图8 不同分组诊断精度Fig.8 Diagnostic accuracy of different groups
3.3.2 卫星监测时序数据实验
采样得到的卫星监测数据为长序列数据,为降低处理计算量,将原始数据在时间维度上降采样15倍,每个阶段随机采样若干个子序列样本,每个样本的序列长度为360,其中70%的样本用于训练,剩下30%的样本用于测试.将选取的3个特征数据在通道维度合并输入网络,网络提取的特征维度设为10维.将提取的特征通过t-SNE方法降维到2维进行可视化,用不同冷暖色调表示数据来源于不同的运行阶段,其中由冷到暖色表示时间增加.
实验结果如图9~10所示,图9为未经过特征提取模型的原始数据,图10为经过无监督模型提取的特征,可以看出,不同阶段数据特征分布具有显著的渐变特性,体现出了运行数据从正常到故障的变化趋势.不同阶段数据仍有小部分重叠,这主要是由于两阶段是在时间上连续过渡的,过渡区域的数据特征比较接近,因此出现重叠的情况.总之,上述特征提取方法可以很好的捕捉不同故障阶段的数据特性,证明了该无监督模型的有效性.
4 结 论
本文主要面向时序序列故障诊断问题,提出了一种基于无监督学习的时序序列故障诊断方法,通过改进最大化互信息这一判别式方法,优化其固定的模型训练模式,并针对时序序列数据的特点优化其局部损失函数,构建了具有稳定收敛性的无监督特征提取模型.在公开数据集的实验结果表明,该方法能够对时序序列数据实现更高的诊断精度,并在某卫星型号监测数据上证实了该方法的有效性,为未来在航天器上实现智能化故障诊断与健康管理奠定了基础.
