基于飞行状态数据的火箭动力系统异常监测研究
2023-08-31程月华李文婷
孙 颢, 程月华*, 姜 斌, 李文婷
1. 南京航空航天大学自动化学院, 南京 211100
2. 北京航天自动控制研究所, 北京 100854
0 引 言
液体火箭发动机是运载火箭上的故障多发部位,其故障严重威胁着火箭发射任务的可靠性和安全性[1-2].开展火箭动力系统的运行状态监测,及时发现异常,可防止非致命性故障对火箭运输任务的影响,提升运载火箭的安全性与可靠性.然而运载火箭动力系统故障传播机理复杂,内部测量信息有限且可信度低,动力系统异常监测极具挑战[3-4].火箭动力系统通过姿态控制回路会影响到飞行器的飞行状态,因此实时动态监测火箭飞行状态信息为开展动力系统异常监测提供了一条有效途径[5].
随着对于火箭动力系统研究的深入,大量学者开展了火箭动力系统异常监测的相关研究,主要包括基于模型、基于信号和数据驱动的异常监测方法.在20世纪90年代末,NASA的喷气推进实验室开发出了基于Livingstone内核的诊断与重构引擎,并首先在深空一号上得到应用[6],这代表了早期基于模型的火箭故障诊断技术.而采用信号处理的方法,利用输出的原始测量信号直接进行故障检测,因其可靠性逐渐受到青睐,国外学者针对航天飞机主发动机(space shuttle main engine,SSME)建立的异常与失效检测系统(SAFD)[7]、飞行加速度计安全关机系统(FASCOS)[8]和涡轮泵振动监控系统[9]都是基于红线阈值报警的方法.近年来,随着专家系统、神经网络方法和模式识别方法等融入到发动机异常检测算法之中,基于人工智能的故障诊断逐渐成为了研究的主流趋势[10].李宁宁等[11]基于发动机试车信号,融合bp神经网络和遗传算法,构建了发动机的非线性辨识模型,最终实现了氢氧补燃发动机的故障检测.SYPA等[12]基于数字仿真模型,结合深度神经网络,提出了一种基于深度学习的液体火箭发动机启动瞬态的异常检测方法.ZHOU等[13]利用极限梯度提升结合卷积神经网络对于发动机的故障诊断与性能退化算法进行了优化.ZHONG等[14]针对燃气轮机开展了数据驱动的故障诊断方法,使用CNN结合SVM的迁移学习方法解决了数据样本较少情况下的故障诊断问题.HUANG等[15]对现有的针对液体火箭发动机故障诊断的算法进行了对比,并给出了综合智能故障诊断模型设计框架,以进一步解决液体火箭发动机的实时故障检测和诊断工程发展的要求.
综上所述,从早期基于模型的故障诊断方法到近期主流的数据驱动的故障诊断方法,学者们针对火箭动力系统故障诊断已经开展了大量的研究工作.由于动力系统部件多、运行工况复杂,可观测参量少,且含大量噪声,仅仅利用动力系统的运行数据来开展故障监测,往往难以获得满意的效果[16-17].本文拟利用飞行状态数据,采用数据驱动的故障诊断方案开展动力系统异常监测研究.首先开展对火箭闭环系统的运行特性分析,选取合适的飞行状态参数形成故障数据集;接着采用长短期记忆神经网络-自编码器(long short term memory-autoencoder,LSTM-AE)进行故障特征提取;最后选取改进的人工蜂群优化支持向量机算法实现动力系统的异常监测.
1 问题描述
1.1 火箭动力学模型
定义运载火箭质心运动动力学方程如下[18]:
(1)
式中,m代表运载火箭质量,V代表火箭的速度,P代表火箭的推力,X2c、Y2c和Z2c代表运载火箭的控制力,X2e、Y2e和Z2e代表运载火箭由于发动机摆动造成的惯性力,α和β代表迎角和侧滑角,θ和σ代表速度倾角和速度偏角,γv代表速度滚转角,FBy、FBz代表干扰力.
定义火箭的绕心运动动力学如下:
(2)
式中,Jx、Jy和Jz代表火箭的三轴转动惯量,ωx、ωy和ωz代表三轴的角速度,Mx1c、My1c和Mz1c分别代表三轴控制力矩,Mx1e、My1e和Mz1e分别代表三轴惯性力矩,MBx、MBy和MBz分别代表三轴下的干扰力矩分量.
由式(2)可知,运载火箭的飞行主要受重力、推力、控制力、惯性力和干扰力的影响,其中控制力和惯性力均会受发动机的摆动影响,发动机摆角也是运载火箭姿态控制系统的控制量,本文考虑十字构型的摇摆发动机如图1所示.
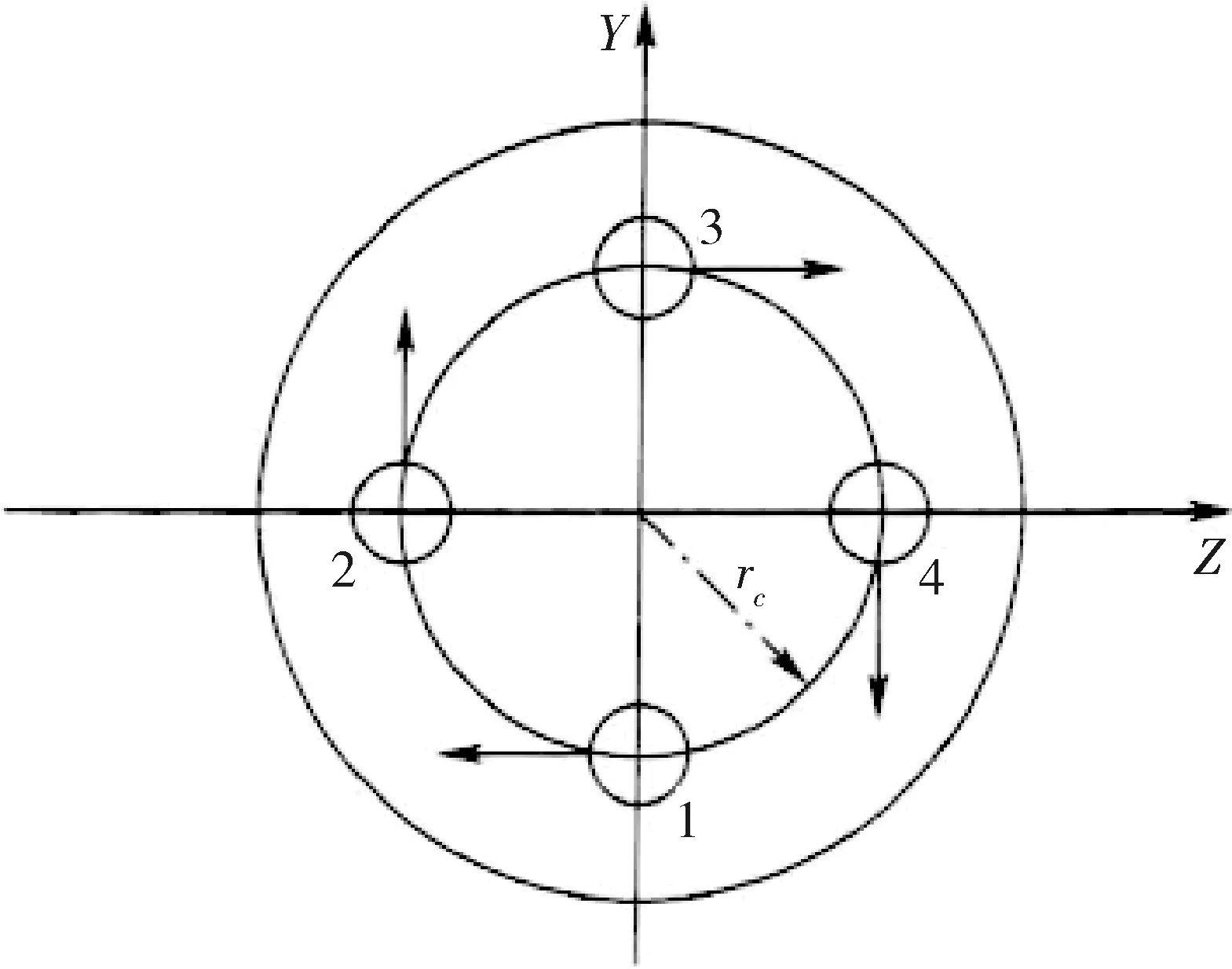
图1 摇摆发动机配置图Fig.1 gimbaled rocket engine configuration
4台发动机编号顺序及偏转角的正向如图1所示,发动机摆角方向定义为从火箭尾端看,顺时针偏转为正.当摇摆发动机摆角为δ1、δ2、δ3和δ4,三通道的等效摆角可以视为
(3)
此时发动机摆动产生的控制力矩为
(4)
式中,xc为发动机摇摆轴至火箭质心的距离,rc为发动机摇摆轴至箭体纵轴的距离.
火箭发动机模型主要由主涡轮泵、预压涡轮泵、燃气发生器、推力室、阀门和管路等部件构成[19],液氧通过氧预压涡轮泵、氧主泵和液氧主阀进入燃气发生器,发生器产生的高温富氧燃气在驱动主涡轮之后,经燃气导管进入燃烧室后进行补燃.燃料煤油经燃料预压泵、燃料一级泵增压后分为四路,其中大部分通过推力室冷却通道进入燃烧室,一部分经燃料二级泵提高压力后流入燃气发生器和推力室点火路,另一部分驱动燃料预压泵后流入主路,最后一部分驱动伺服机构.
如式(5)所示,根据动量定理,火箭发动机的推力如下:
F=[qeve+(pe-pa)Ae]ηcηn
(5)
式中,qe为喷管出口流量,ve为喷管出口理论喷气速度,pe为喷管出口压力,pa为外界大气压力,Ae为喷管出口截面积,ηc为燃烧效率,ηn为喷管效率.
在火箭飞行过程中,发动机模块接收到推力指令,利用闭环或开环控制得到相应的推力,输出实际推力,因此发动机的故障,例如涡轮叶片烧蚀故障或泵气蚀故障等均会直接影响推力,推力变化又会影响到控制力、控制力矩等,最终作用于飞行姿态控制系统,影响火箭的飞行姿态.
1.2 问题提出
液体火箭发动机各个部件之间紧密耦合,相互联接组成为了一个整体,由于液体火箭发动机本身复杂的结构和其所处恶劣的工作环境,当发动机运行一段时间后,发动机的各个部件由于高温、高压和腐蚀损坏等原因会发生不同程度的故障或性能退化.这些因素使得实际发动机会产生部件效率的降低及参数的偏差,引起发动机推力等性能参数相比于设计值产生损失,因此本文将推力异常作为主要的故障表征开展研究.
由于飞行中的发动机内部测量传感器的数量有限,且观测数据可能受到测量误差、噪声和采样率不足或遮挡等因素的影响,使得获取的信息不完整,这给系统分析、预测或控制带来挑战.基于飞行状态数据和控制系统数据,开展“弱观测条件下”的异常监测研究为火箭发动机故障诊断提供了一条有效途径.
由上所述,执行机构故障和发动机推力异常故障均会对飞行参数产生影响,因此如何合理利用数据的信息开展动力系统异常监测是一个难点,本文利用LSTM-AE重构算法和基于人工蜂群寻优的支持向量机(support vector machine, SVM)分类算法实现了基于飞行状态信息的动力系统异常监测,算法框架如图2所示.
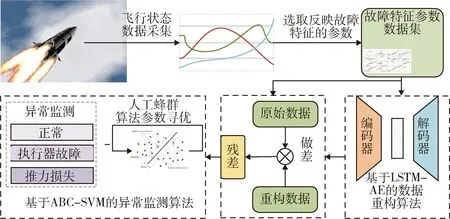
图2 异常监测算法设计框图Fig.2 Diagram of anomaly detection scheme
2 基于LSTM-AE的特征提取算法
由于火箭飞行过程中,故障影响下的飞行状态数据难以完全表征故障特性,因此需要使用算法提取飞行状态数据的特征,使得正常和异常数据更容易区分.
特征提取是异常监测中的基础问题[20],通过算法对于数据进行预测或重构,可以充分利用火箭飞行状态时序信息的同时,提取能够对应不同故障类型的数据特征[21-22].本节利用LSTM-AE搭建正常飞行状态数据间的映射模型,对正常数据进行重构,生成残差以强化故障特征.
自编码器由输入层、输出层和隐藏层3层神经网络构成,其目标是使输出结果和输入结果尽可能相似,其由编码网络与解码网络两部分构成,编码网络的主要目标即为将输入数据从高维空间压缩到低维空间,实现输入到编码的映射,构建出输入数据的主要特征;解码网络的主要目标即为实现近似输出,通过将隐藏层低维数据映射到高维空间进行重构并使得误差最小化以达到复原数据的目的[23].
h=f(xi)=σ(W1xi+b)
(6)
式中,h为隐藏层表征值,f为编码函数,σ为Sigmoid函数,其经常作为编码过程的激活函数,W1为输入层与隐藏层之间的权值矩阵,b为编码网络的偏置向量.Sigmoid函数可以表示为
(7)
同样的,对于解码网络而言,隐藏层表征值h用于重构输出值ym并使其尽可能于输入xm相等,解码过程可以描述为
ym=g(h)=σ(W2h+d)
(8)
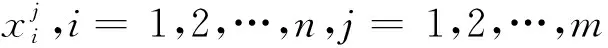
(9)
训练过程中采用梯度下降方法对于自编码器网络参数进行更新.
自编码器对于飞行状态数据集进行重构,而通过结合LSTM网络,其可以捕捉数据间的时序关系,并以降噪的低维形式对于数据进行重构.
LSTM-AE仍然是一个多层次结构,其编码器和解码器都为LSTM模型.基于编码器部分对火箭飞行状态冗余信息进行压缩,从而获得系统状态数据的最小表达,并通过解码器部分根据最小表达解压反算出原信号.LSTM-AE的结构如图3所示.
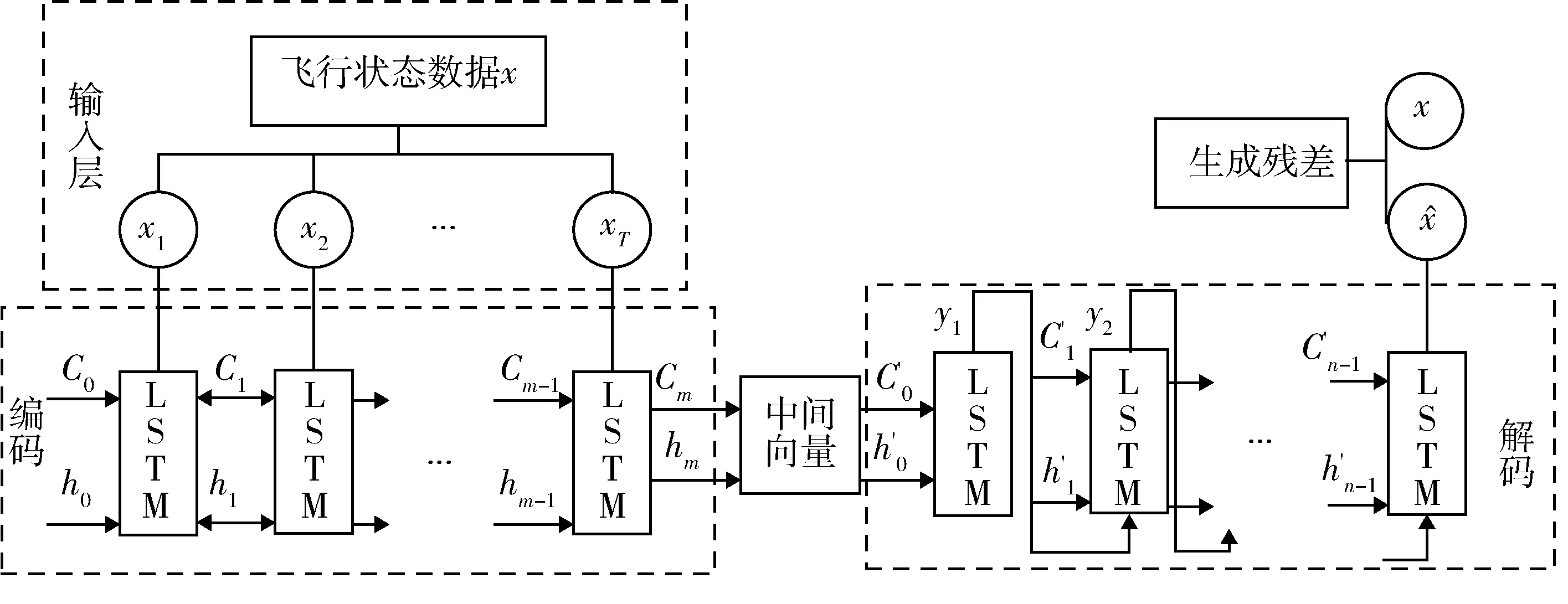
图3 LSTM-AE网络结构Fig.3 LSTM AutoEncoder network structure

本文仅采用正常数据点对于自编码器模型进行训练,经过训练后,自编码器能够重建正常数据点,并与原始数据之间保持一个较小误差,而当其重构一个异常数据点时,误差将会远大于正常情形,通过将重构后的值与原值做差,可以得到特征强化后的残差数据集,此时故障情况下的残差会远大于正常情况的残差.
3 基于ABC-SVM的异常监测算法
在形成残差数据集后,利用训练好的SVM模型捕捉参数集的数据组合关系,由于在正常、执行机构故障和动力系统故障情况下的残差特征不同,利用SVM分类模型可以利用分类能力实现动力系统异常的监测.由于SVM的参数设定对于其性能影响较大,因此本节引入人工蜂群优化(artificial bee colony algorithm,ABC)算法对于SVM中的参数进行优化,以实现更精确的数据分类.
3.1 支持向量机算法
支持向量机算法是一种用于分类的机器学习模型,其在线性分类器的基础上通过引入最优化、VC维等理论构建而成,可以解决多种工程技术领域的分类问题.
对于二分类问题,支持向量机会在二维平面内构建一个直角坐标系,将需要分类的样本转换为坐标向量,使所有样本都包含在所构建的直角坐标系中,并在此坐标系中构建一个使两种样本都尽可能全部分开的超平面,而超平面所在位置的设定应使距离它最近的正负样本个体尽可能远离这个平面,使多种样本能够划分的更加明显、精细.
对于给定的数据集(xj,yj),j=1,2…,m,其中x∈Rd为输入向量,yj∈{-1,+1}为类别,基于线性优化理论可将超平面的确定问题转化为约束优化问题,如下所示:
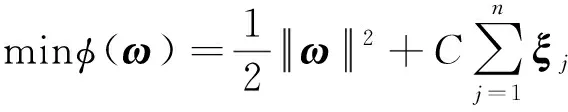
(10)
式中,ω和b为超平面的法向量和平移距离,ξj为松弛变量,用以提高模型的泛化能力;c为惩罚因子,用以权衡分类损失和最大间隔的关系.
此时将式(9)改写为
y(ω)=-yj(ωTxj+b)+1≤0
(11)
将式(11)表示为拉格朗日函数,并构造对偶问题可得下式:
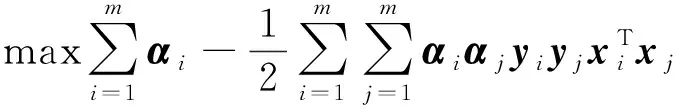
(12)
解出α可以得到如下的模型:
(13)
SVM使用核函数将数据转换到高维空间,此时在高维空间内的数据也线性可分.通过核函数k(xj,x)=[φ(xj),φ(x)]可以得到分类器的表达式如下:
(14)
本文选用径向基(radial basis function,RBF)核函数作为映射函数,其表达式如下所示:
(15)
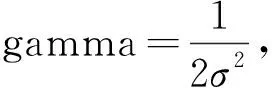
3.2 人工蜂群参数优化算法
如上文所述,基于SVM的分类算法的重要参数有核函数参数gamma和惩罚因子c,其取值对于算法的性能有着较大的影响.相比于遗传算法来说,人工蜂群算法在局部的收敛和寻优能力上要更为出色,且其控制参数较少,鲁棒性强,因此本文选用人工蜂群算法对于SVM分类器参数进行寻优[24].
如图4所示,核函数参数gamma的取值大小与SVM的分类精细程度密切相关,图中实线为决策平面,虚线上的样本为支持向量,若取值较大,空间映射维度过高,SVM易出现过拟合现象;反之则易发生分类准确率较低的情况,误判一些特征相似样本,因此选择合适的核函数参数gamma数值对提高SVM的性能很关键.

图4 SVM参数对算法性能的影响Fig.4 The effect of the parameters of the SVM
此外,惩罚因子c决定了支持向量和最优分类超平面的距离,如图4所示,当数值c越大,模型对错误分类的容忍程度越小,分类也越准确,但其泛化能力会降低;c数值越小,模型的容错程度越高,对于测试样本的判断能力更差.因此选择合适的参数对于提升模型的分类精度有重要的意义.
本文使用一种人工蜂群算法对于SVM的参数c和gamma进行寻优,为SVM算法的准确分类奠定基础.
人工蜂群算法模拟蜜蜂的采蜜过程,其中蜜源表示优化问题可能的最优解,含蜜量代表解的适应度,蜂群搜索蜜源的速度即优化目标的求解速度.
算法包括3类蜂群角色:引领蜂、侦察蜂和跟随蜂.算法首先根据下式产生SN个初始解如下:
(16)
式中,f∈(1,2,…,M),fi,j为蜜源的第j维分量.
此时则有SN个引领蜂和蜜源.此时蜜源为M维向量Fi=(fi1,fi2,…,fiM,i=1,2,…,SN),M对应优化参数的数目,之后计算每个解所对应的适应度.
引领蜂在一定的概率下对记忆中的蜜源进行领域搜索,若找到含蜜量更高的蜜源,则会用新蜜源位置代替旧蜜源位置,同时计算出新解的适应度,否则保持原始位置不变.当所有引领蜂完成搜索回到蜂巢,将搜索到的信息(蜜源位置和适应度)传达给跟随蜂,跟随蜂按照找寻到的信息按一定的概率去跟随,并按照引领蜂的方式对记忆中的位置进行改变并确认新的蜜源的含蜜量.
(17)
式中fit代表第i个蜜源的适应度值,表达式如下:
(18)
若某个蜜源Fi连续经过给定的循环次数后一直未被替换,则该位置的蜜源将被放弃,同时此处的引领蜂将转变为侦察蜂,该侦察蜂则重复式(16)随机产生初始值以代替Fi,并计算出新蜜源的适应度值,通过以上步骤完成了最优参数的搜索.
4 实验验证
4.1 闭环数字仿真回路
为了对于所提算法进行验证,本文建立了火箭系统闭环数字仿真回路,由其结构如图5所示.
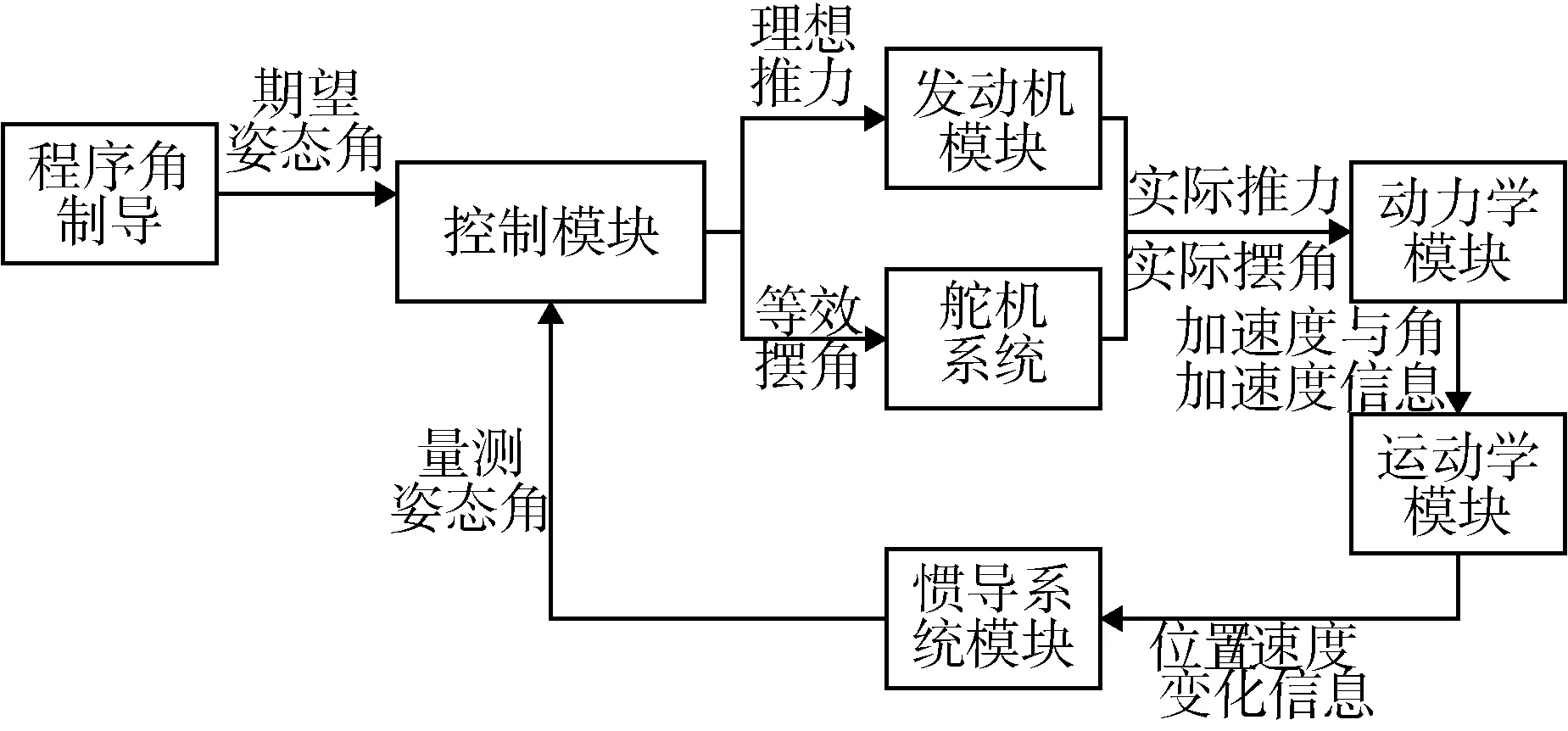
图5 闭环数字仿真回路示意图Fig.5 Schematic of a closed-loop digital simulation
闭环数字仿真回路由惯导、制导、控制、发动机、执行器和动力学6个模块组成,控制模块接收事先设定的程序角指令,输出发动机摆角控制指令至舵机系统,舵机系统输出发动机真实摆角送至动力学模块进行动力学和运动学的解算.通过闭环数字仿真回路可以实现数据的生成与故障数据的获取,为后文的算法验证提供基础.
4.2 实验数据集
本文利用数字仿真平台结合故障注入的数据对于所提算法进行了验证.通过数字仿真平台模拟火箭的主动段飞行,考虑到角速度、过载参量与火箭所受外力有着明确的数学关系,而发动机指令摆角作为控制系统的核心参数与当前的姿态控制效果直接相关,选取飞行状态可测参数与控制系统指令参数构成如下飞行状态数据集:
X={ωx,ωy,ωz,ny,nz,δφ,δψ,δγ}
(19)
其中ωx,ωy和ωz代表三轴角速度,ny,nz代表法向过载和轴向过载,δφ,δψ和δγ代表三通道的指令摆角.
在火箭闭环控制仿真系统中分别注入推力异常和执行机构卡死故障,开展算法仿真.推力异常故障表达式如下:
(20)
其中Δ代表故障因子.
执行机构卡死故障表达式如下:
(21)
式中Cδ代表某一发动机摆角卡死的角度.
将数据集在LSTM-AE模型中进行重构,与实际信号相比,得到残差信号.本节以动力系统推力损失故障为例,为了体现模型的泛化效果,在训练集中选取推力损失10%的数据集,测试集中选取推力损失20%的数据集,重构算法效果如图6所示.

图6 lstm-ae重构参数图(推力损失10%)Fig.6 lstm-ae reconfiguration parameters
由图6可见,自编码器在正常的前600 s可以捕捉到飞行参数的特征并完成重构,在异常阶段则不能完成信号的重构,因此通过残差信息即可表征故障的发生.
将残差信息输入ABC-SVM模型中,经过蜂群优化算法,可得最优参数c=84.201 9,gamma=89.543 6.将本文所提算法与LSTM预测-ABC-SVM分类算法、LSTM预测-SVM分类算法对比,用混淆矩阵表示分类结果如图7所示.
针对动力系统异常的监测算法评价指标如表1所示,在多分类问题中,将动力系统故障视为一类,正常和执行机构故障视为另一类,据此转化为二分类问题计算评价指标.
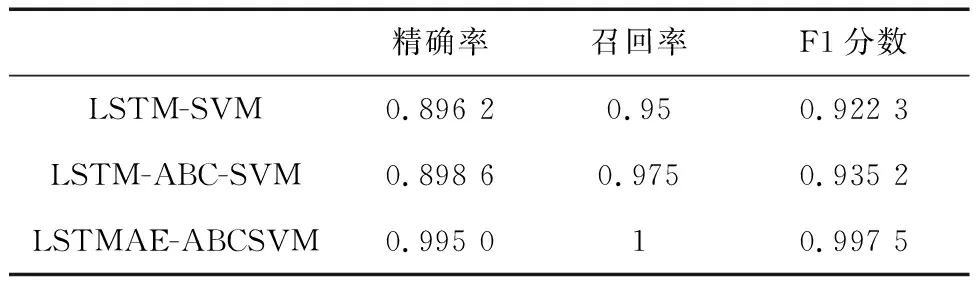
表1 算法性能指标对比(动力系统异常监测)Tab.1 Performance comparison of each algorithm
由图7和表1可见,本文所提的算法针对动力系统异常,相对于传统的LSTM预测生成残差或改进前的SVM算法,性能都有一定的提升,在复杂的数据类型中可以准确地利用飞行量测信息及控制系统信息定位动力系统的异常.
5 结 论
本文针对弱观测条件下的火箭动力系统异常监测问题,从火箭数字闭环仿真回路中选取飞行状态信息,构建故障数据集;然后利用LSTM-AE模型对于飞行状态数据集进行重构生成故障特征;接着使用人工蜂群优化的支持向量机算法对于残差数据集进行分类以实现动力系统异常监测;最后利用数字仿真平台结合故障注入生成的数据对于所提算法进行了验证,结果显示本文所提算法能够利用飞行状态参数及控制系统参数,基于分类算法实现动力系统的异常监测,且监测准确率优于传统的基于预测的异常监测方案.
本文所提算法只针对推力损失这一种典型故障进行了研究,后续将深入开展动力系统其他故障情形下的异常监测与诊断问题.
