状态划分下基于Bi-LSTM-Att的轴承剩余寿命预测
2023-08-31陈东楠胡昌华郑建飞张建勋庞哲楠
陈东楠, 胡昌华, 郑建飞, 裴 洪, 张建勋, 庞哲楠
1. 火箭军工程大学, 陕西 710025
2. 中国人民解放军96901部队, 北京 100094
0 引 言
旋转机械是一种高速旋转的生产设备,在制造业、航空航天、冶金和军工等行业发挥着至关重要的作用.滚动轴承作为此类设备中最重要的承载部件之一,总是在极端恶劣的环境下运行,如极端转速、高环境温度、潮湿和过载等[1].且滚动轴承的任何错位、故障或损坏都可能导致设备停机,甚至引发严重的安全事故.因此,预测和健康管理(prognostics and health management,PHM)技术是保证旋转机械系统安全可靠运行的关键[2],其中,RUL预测作为PHM技术的基础与核心,高效准确的RUL预测对滚动轴承具有十分重要的实际意义[3].
目前,滚动轴承RUL预测方法主要包括以下3种[4]:基于物理模型的方法、基于统计模型的方法以及基于机器学习的方法.基于物理模型的方法,它是基于机械参数构建的,如工作条件、材料疲劳强度和失效标准[5].然而,基于物理的模型通常是为特定设备或系统开发的,构建成本昂贵.此外,预测准确性不可避免会受到外界环境的影响.相对于传统物理建模方法而言,基于统计理论的数据驱动方法能够反映滚动轴承的真实动态行为,无需根据系统内部复杂的退化机理建立特定的预测模型,从而能够克服上述缺点.通过建立基于经验知识的统计模型估算轴承的RUL,普适性更高,但同时也依赖于大量数据进行状态估计.
近年来,由于人工智能的快速发展,基于机器学习的方法已成为解决RUL问题最有效的方法之一.这类方法直接从退化状态数据入手,通过提取原始振动信号的敏感特征,再输入到机器学习算法模型中进行RUL预测.AHMAD等[6]从时域中筛选特征构建健康指标,采取基于回归的自适应模型预测轴承的性能退化趋势.MAHAMAD等[7]选择均方根作为输入特征,釆用ANN模型进行训练,最大化地减少劣化噪音带来的影响,从而提髙预测精度.尽管以上研究采用的预测模型方法各异,但本质均为建立退化特征到RUL预测值的非线性映射模型.所以筛选出蕴含丰富退化信息的敏感特征,将直接影响后续对滚动轴承进行退化趋势预测的效果.
目前现有的轴承RUL预测方法中大都针对单一退化过程,即对全周期RUL进行预测,但实际中轴承的退化过程呈现出多阶段的退化趋势.ZHANG等[8]在研究滚动轴承的退化过程中,发现设备的退化过程呈现出分阶段退化现象.JIN等[9]基于轴承全寿命周期状态监测,将滚动轴承的退化阶段划分为健康阶段和磨损阶段,使用Box-Cox变换和高斯分布找到故障异常点,实现磨损期的RUL预测.然而,滚动轴承在长期服役条件下,其全寿命周期一般分为3个不同阶段,但现有大多数相关研究中,一般仅通过确定出异常监测点后将滚动轴承的监测状态划分为2阶段,并未充分考虑到3个阶段退化状态的差异性.所以实现滚动轴承各个阶段的划分对于后续RUL预测显得尤为关键.
为了进一步提高预测模型的准确度,主要技术难点在于搭建适用于时序数列进行RUL预测的网络模型.然而,传统的深度学习方法未考虑轴承退化序列的时序性质,无法取得较为准确的预测效果,因此需构建更加关注时序信息的预测网络.循环神经网络(recurrent neural network,RNN)善于处理时间序列.GUO等[10]采用基于RNN提取表征滚动轴承退化特征量的算法实现滚动轴承较高精度的剩余有效寿命预测.但也带来了一些问题:如较长的时间序列或较多的神经元在训练时会出现梯度消失、梯度爆炸等问题.LSTM网络在一定程度上解决了RNN处理长序列的局限性,但该网络仅考虑过去信息而忽略未来信息.在此基础上,引入Bi-LSTM网络能够以前向和后向2种方式捕获数据间的动态依赖性,进一步提高模型的收敛速度和降低预测误差.如韩林洁等[11]运用Bi-LSTM网络对滚动轴承剩余使用寿命进行预测.康守强等[12]提出一种基于改进SAE和Bi-LSTM的滚动轴承RUL预测方法,改进了模型的预测误差.然而上述文献仅在全寿命周期数据上进行RUL预测实验,忽略了正常状态和快速失效阶段数据带来的干扰,未考虑不同退化阶段下退化规律具有显著差异性的问题,此外,上述文献均假定深度学习模型所提取的特征对于预测结果的贡献率是一致的,直接影响了预测结果的准确性.
综上,由于实际工程中原始数据包含大量随机噪声和干扰,难以全面准确地表征轴承的运行状态.而均方根特征在全寿命周期中表现出良好的单调趋势,且符合轴承的退化规律曲线,故本文选取该时域特征作为健康指标.针对传统滚动轴承全寿命周期中RUL预测精度低、波动性大的问题,本文提出一种新型滚动轴承退化状态划分方法.通过引入Mann-Kendall检验法进行趋势判别,确定出退化趋势的起始点,再结合归一化奇异值相关系数法确定出慢速退化期终止点,从而确定出滚动轴承全寿命周期中的慢速退化阶段,避免了处于健康阶段的数据较长导致的数据冗余以及快速失效期数据难以有效利用且具有不确定性的问题.最后,在Bi-LSTM预测模型上融入注意力机制,可以从输入的长序列中自动提取出对预测结果贡献度较高的特征,赋予更高的权重,进一步提高预测模型的精确度.
1 融合Mann-Kendall检验与奇异值分解的退化状态划分
滚动轴承从开始运作直至失效是一个逐渐变化的性能退化过程,随着工作过程中环境、载荷等因素对滚动轴承造成的磨损,轴承的性能逐渐减弱,退化程度逐渐加深.当性能下降到一定程度后,滚动轴承进入失效期,此时需要更换轴承部件.因此,滚动轴承的全寿命周期变化情况可划分为平稳期、慢速退化期和快速失效期3个阶段.准确的状态划分为后期网络模型对滚动轴承RUL预测提供了前提条件.为了表征滚动轴承性能退化趋势的变化规律,本文对原始振动信号数据进行特征提取,选取均方根作为健康指标,并在均方根时域特征上进行状态划分如图1所示.

图1 滚动轴承的均方根随时间的变化图Fig.1 Variation of the root mean square of rolling bearing with time
滚动轴承的振动信号在正常运行时呈现相对平稳的特征,变化缓慢,但这也使得RUL预测变得更加困难.因为健康阶段的数据过多、冗余且信噪比低,输入数据无法充分利用,可能会导致RUL预测的不可靠性和波动性.因此,本文采用状态划分算法来判断滚动轴承的工作状态,通过引入Mann-Kendall检验法确定出慢速退化期的起始点,再结合归一化奇异值相关系数法确定出慢速退化期终止点,从而实现滚动轴承的状态划分,有效减少正常状态数据和失效数据对后续RUL预测精度的干扰,提高模型的寿命预测精确度,整体方法流程图如图2所示.

图2 方法流程图Fig.2 Flowchart of the proposed method
1.1 特征提取
在滚动轴承退化状态评估中,选择合适的特征来表征性能退化趋势是非常重要的.这些特征可以作为健康指标,成功检测退化阶段的开始,区分轴承的健康和故障状态.现有研究表明,从时域的原始数据中提取特征比在频域中更适合实时RUL预测[13].原始数据对外部扰动非常敏感,例如意外的振动、湿度和温度,这些扰动破坏了数据采集过程并掩盖了真实的系统响应.为了避免上述缺陷,本文选择了从时域振动信号中提取的均方根(root mean square,RMS),因为它无需对振动信号进行预处理,直接分析采集到的振动信号即可,因此不会丢失轴承运行信息,其具有明显随时间变化的趋势,轴承发生故障时,均方根会显著增大.因此,本文采用振动信号的RMS值来确定轴承退化阶段.
(1)
式中,xt={xt(1),xt(2),…,xt(N)},N表示长度为N的输入序列.
1.2 Mann-Kendall趋势检验
Mann-Kendall检验法是一种非参数检验方法[14-15],经进一步完善和优化,可检验序列的变化趋势和突变出现时间.其主要优势在于对长时间轴承监测序列的趋势与突变分析中,Mann-Kendall检验不需要样本遵循一定的分布,也不受少数异常值的干扰,能够很好地揭示整体监测时间序列的突变情况与趋势变化.
对于具有n个样本量的时间序列xi(i=1,2,…,n),对于所有的k,j≤n,且k≠j,xk和xj的分布并不相同,检验的统计变量S计算如下:

(2)
式中,sgn(·)为符号函数,具体表示如下:

(3)
统计量S为正态分布,其均值为0,方差Var(S)为
(4)
当输入为长时间序列时,即n>10时,标准正态统计变量计算过程如下:

(5)

(6)
(7)
在时间序列为随机的假设下,定义统计量
(8)
(9)
(10)
UFk为标准正态分布,UF1=0,UFk是根据时间序列xi计算出的统计序列,再按照时间序列逆序xn,xn-1,…,x1,重复进行上面的步骤,得出UBk统计序列,同时令UBk=-UBk(k=n,n-1,…,1),UB1=0.给出置信水平α,如果α=0.05,查正态分布表,得临界值u0.05=±1.96.
通过对统计序列UFk和UBk的分析可深入分析序列xi的变化趋势.当UFk>0时,序列呈上升趋势,反之呈下降趋势,若UFk超过临界值时则说明上升或下降趋势显著.
1.3 归一化奇异值相关系数
自19世纪70年代以来,BELTRAMI[16]和JORDAN[17]先后提出了实正方矩阵的奇异值分解(singular value decomposition,SVD),并在之后不断改进完善.该方法已成功应用于信号降噪、特征凸显、数据降维、数据压缩和模式识别等多个领域.奇异值分解从含有噪声的数据中抽取相关特征,实现数据中噪声或冗余信息的去除.因此,通过SVD分解,可以有效去除噪声,实现数据重要特征的提取.
传统SVD方法对一维信号进行处理时,采用Hankel矩阵进行相空间重构.对于序列长度为N的离散信号x=[x1,x2,…,x(N)],得到的Hankel矩阵如下:
(11)
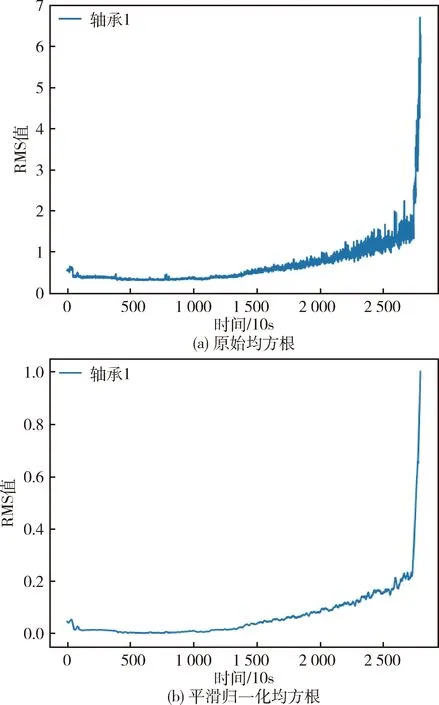
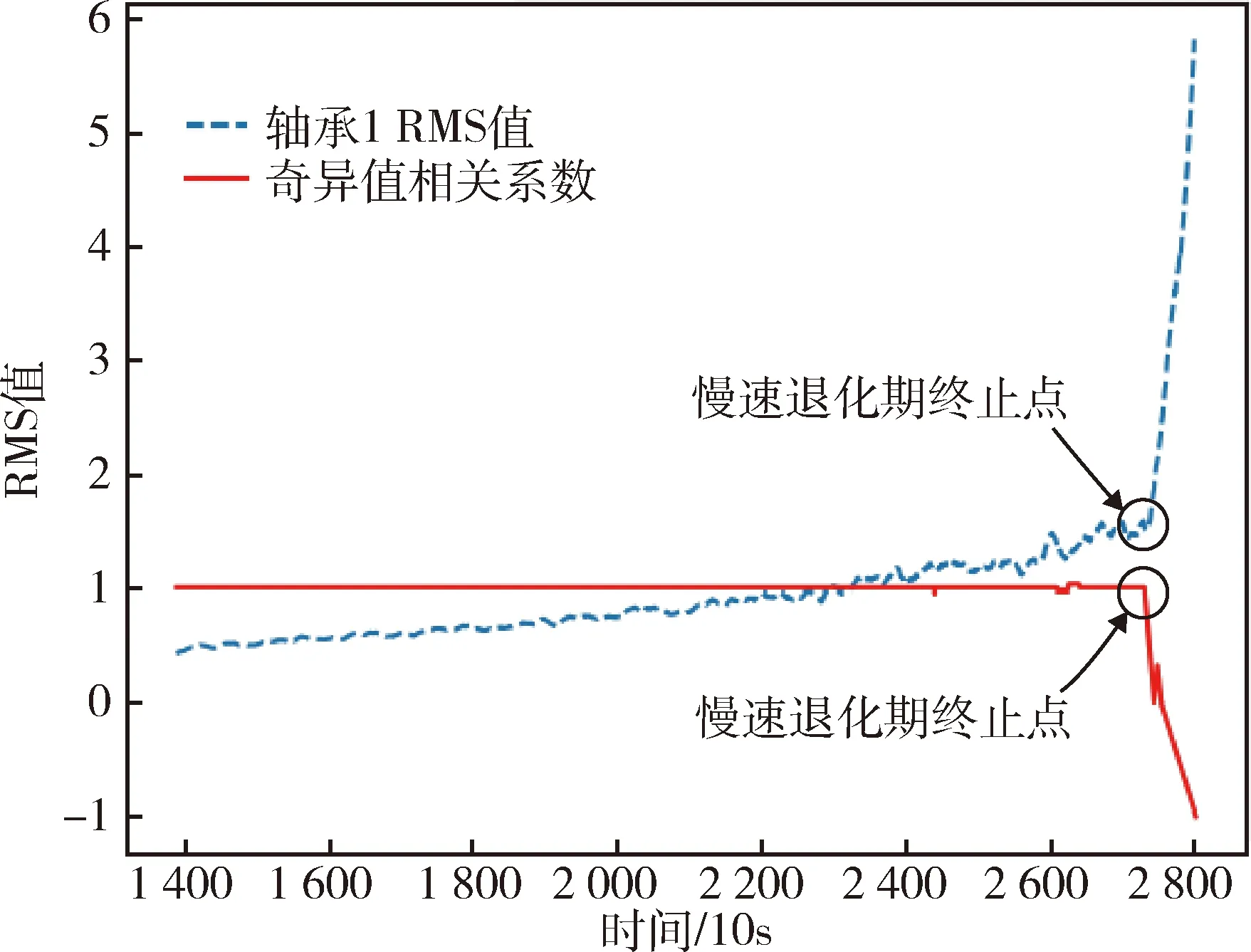
式中,N是信号长度,m为矩阵行数,n为矩阵列数,1 对矩阵H进行奇异值分解,令H∈m×n,则存在正交矩阵U∈m×m和V∈n×n使得 H=UΣVT (12) (13) 式中,N是序列划分段数,q是矩阵H非零奇异值的个数. 因为相关系数位于区间[-1,1],所以对获取的奇异值矩阵进行归一化处理,采用式(14)对矩阵M进行归一化 (14) 在轴承振动过程中,正常状态的样本之间,奇异值矢量的相关性较高,而正常状态和故障样本之间,相关性则不足,反映在相关系数曲线上则是一条递减的曲线.由于奇异值具有良好的数值稳定性,当信号发生扰动时,奇导值的变化较小.当信号发生较大的变化时,奇异值的变化则较大,以此来避免局部噪声和细微信号变化对状态划分的影响,从而能够准确识别发生剧烈变化时的信号状态.相关系数计算如下: (15) 式中,x、y分别为归一化奇异值矩阵的奇异值矢量,j=1,2,…,N. 双向长短期记忆网络(Bi-LSTM)由前向LSTM和后向LSTM堆叠而成,是对LSTM网络的一种改进.相比于传统循环网络,LSTM有效解决了梯度消失、梯度爆炸与长期依赖等问题.而Bi-LSTM在LSTM的基础上,通过前向层和后向层同时完成对输入序列的处理,充分学习监测数据过去与未来的潜在时序信息,能够更加深入地挖掘退化数据的时序信息,可以有效提高预测结果的准确性[18],其结构如图3所示. 图3 Bi-LSTM网络结构示意图Fig.3 The structure of Bi-LSTM Bi-LSTM网络中正向和反向传递计算公式如式(16)~(20)所示,正反向输出的拼接公式如式(21)所示. it=σ(Wixt+Uiht-1+bi) (16) ft=σ(Wfxt+Ufht-1+bf) (17) ot=σ(Woxt+Uoht-1+bo) (18) Ct=ft×Ct-1+it×tanh(WCxt+UCht-1+bC) (19) ht=ot×tanh(Ct) (20) (21) 式中,ft、it和ot分别是LSTM中的遗忘门(forget gate)、输入门(input gate)和输出门(out gate),Ct、ht分别表示细胞状态(cell state)和隐藏层状态(hidden state),σ、tanh分别表示Sigmoid激活函数与双曲正切激活函数,W、U为权重矩阵,b为偏置. 为了捕捉对预测结果贡献度较高的特征,本文在Bi-LSTM网络中引入注意力机制(attention)层,将对输出结果中影响预测效果的关键特征赋予更高的权重.这样就可以充分利用每个时间步的隐藏状态,提取有用信息. 在Bi-LSTM网络结构中融合注意力机制,将Bi-LSTM层的输出结果H=[H1H2H3…Hn]作为注意力机制的输入,attention层对输出结果分配不同的权重,其中利用式(22)计算M和随机初始化参数矩阵ωT的相似度并利用softmax进行归一化处理得到标准化权重α.将得到的权重αT与Bi-LSTM的输出结果H相乘得到加权输出r.将r通过全连接层映射可得到t时刻的网络输出结果y. M=tanh(H) (22) α=softmax(ωTM) (23) r=HαT (24) y=σWhy[r]+bhy (25) 式中,tanh表示双曲正切激活函数,M为H进行非线性变换得到隐含表示,Why为全连接层的权重矩阵,b为全连接层的偏置. 本文在状态划分下进行RUL预测.首先获取轴承的振动信号,将慢速退化期的数据从原始振动信号的时域特征序列中截取出来,然后进行数据预处理,分析截取特征值与滚动轴承RUL之间的映射关系.将该特征值通过滑动时间窗处理技术得到具有局部依赖性的输入样本,对应的RUL规范值作为标签.把处理好的样本分为训练集和验证集,将训练集输入Bi-LSTM-Att模型中进行训练,在验证集上预测滚动轴承的RUL. 其中,Bi-LSTM-Att网络训练过程中,将预测值与样本标签进行对比,将每次迭代得到的输出误差进行反向传播优化网络模型中的参数.其中,网络训练标签为以轴承慢速退化期起始点到慢速退化期终止点作为轴承的全部寿命值,再进行归一化处理,使其范围处于[0,1]区间之内,从而消除不同轴承之间的差异. (26) 式中,N为轴承全寿命周期值,n为轴承慢速退化期的全寿命值,Ti为当前时刻值,Tk退化期起始点,yi为轴承在i时刻的RUL百分比. 本文选用IEEE PHM 2012数据挑战赛滚动轴承加速寿命试验(accelerated life testing,ALT)的公开数据集.通过PRONOSTIA数据采集平台,实现分别在加载不同载荷与转速的情况下,利用安放在水平和垂直方向上的加速度传感器和温度传感器收集滚动轴承全寿命周期的振动数据与温度数据[19].本文采用轴承的水平振动加速度数据进行验证. 在试验过程中,通过连续窗口采集振动加速度信号,每10 s采集一次,持续时间为0.1 s,采样频率为25.6 kHz,即每个采样点包含2 560个振动信号样本.该数据集包含了3个不同工况下的轴承数据:工况1下发动机转速为1 800 r/min,负载为4 000 N;工况2下发动机转速为1 650 r/min,负载为4 200 N;工况3下发动机转速为1 500 r/min,负载为5 000 N.在本试验中,选择工况1下7个轴承的振动信号进行测试,这些轴承均可提供从正常到故障全寿命周期退化过程的振动信号. 实际轴承的原始振动信号中存在着大量能够反映其健康状态的退化信息,如图4所示,以轴承1全寿命周期的振动信号为例,可以观察到,随着轴承工作时间的增长,晚期振动幅值明显增大,说明轴承退化加剧,接近失效. 图4 滚动轴承1全寿命周期退化趋势时域图Fig.4 Time domain diagram of the degradation trend of rolling bearing1 throughout their entire life cycle 数据预处理即对滚动轴承原始振动信号进行一定的处理措施,本文数据预处理主要包括3个部分: 1)从原始振动信号中挖掘出能够准确表征轴承性能退化过程的特征,是实现后续退化状态评估和RUL预测的大前提.由于RMS特征值在全寿命周期中表现出良好的单调趋势,符合轴承的退化趋势规律,故试验选取RMS作为健康指标进行状态划分.图5(a)为从原始信号中提取的全寿命周期RMS特征值. 图5 滚动轴承1均方根随时间变化图Fig.5 Root Mean Square variation of rolling bearing1 2)在实际的滚动轴承状态监测中,由于外部干扰的存在,所得到的数据经常包含大量随机噪声,因此需要对RMS值进行滤波以去除噪声.本文采用Savitzky-Golay滤波器对RMS值进行处理,该滤波器使用多项式拟合来估计信号的趋势,并从信号中减去该趋势,使信号更加平滑,有利于后续分析. 3)为了得到更好的神经网络预测结果,需对数据进行归一化处理,本文采用min-max归一化法对降噪后的数据进行处理,如图5(b)所示. (27) 式中,xt为设备在t时刻的监测数据,max(x)和min(x)分别为设备所有时刻监测数据的最小值和最大值,xnt是归一化后的值. 首先采用Mann-Kendall检验法确定轴承特征序列的变化趋势和变化出现时间.对于n个特征值序列x={x(1),x(2),…,x(n)},原假设H0:该序列无趋势,备择假设H1是双边检验。在给定的显著性水平α=0.05下,若|UFk|≥UF1-α/2拒绝原假设,即在0.05置信水平上,时间序列数据存在明显的上升或下降趋势;若|UFk| 图6 轴承1退化趋势判别统计量随时间变化图Fig.6 Variation of degradation trend discriminant statistics of bearing1 over time 由轴承1实验结果知,当采样点在1 335时,UFk值大于0,表明退化趋势呈上升趋势;当采样点在1 390,UFk超过临界值1.96时,表明上升趋势显著.由此确定出轴承1退化期起始点.若正序列UFk和反序列UBk统计量序列在置信度区间之间存在交叉点,则表明该交叉点为突变点,确定出轴承的慢速退化终止点,但由图6可以观察到,正序列UFk和反序列UBk2个统计量序列在给定的显著性水平临界线之外存在交叉点,则不确定该点是否为进入快速失效期的突变点[20]. 由于Mann-Kendall检验能够很好地揭示整体时间序列的突变情况与趋势变化,故采用该方法可得到工况1下7个轴承的初始退化点,如表1所示. 表1 工况1下7个轴承的退化起始点Tab.1 Starting point of degradation for 7 bearings under condition 1 为有效表征轴承的RUL,必须确定出其寿命结束时刻,即慢速退化期终止点的确定.本实验通过归一化奇异值相关系数走势确定出慢速退化期终止点.如图7所示,当轴承处于正常运行状态时,相关系数曲线保持稳定.当轴承状态发生剧烈变化的时候,曲线值急速下降,由此可有效识别快速失效的起始部分.本实验认定当相关系数值小于0.95时,此时对应的采样位置为慢速退化期终止点. 图7 轴承1奇异值相关系数和RMS随时间变化图Fig.7 Singular value correlation coefficient and RMS of bearing 1 over time 图8为工况1下的7个轴承的时域特征RMS,可以明显观察到,在同样的工况下的外观相同的轴承实际退化趋势大不相同,所以不同滚动轴承的退化状态划分是不同的.通过上述算法确定出7个轴承的慢速退化终止点,如表2所示. 表2 工况1下7个轴承的慢速退化终止点Tab.2 Slow degradation endpoint of 7 bearings under condition 1 图8 工况1下7个轴承RMS随时间变化图Fig.8 RMS of 7 bearings over time under condition 1 确定出滚动轴承的慢速退化阶段,再进行RUL预测,不仅能够有效节约计算资源.同时还能够有效减少正常状态数据和失效数据带来的干扰,从而提高模型寿命预测的精确度和稳定性. 在采用预处理后的慢速退化期数据进行RUL预测时,首先采用窗口长度和步长分别为10和1的时间窗处理技术生成固定长度的训练样本,并计算出每个训练样本对应RUL标签.RUL标签为滚动轴承归一化的剩余使用寿命百分比.然后,把经上述处理的数据输入到Bi-LSTM-Att网络实现RUL预测. 按照如下方法设置实验:依次挑选4个轴承数据离线训练,得到基于Bi-LSTM-Att网络的预测模型,实现对其余2个轴承的RUL在线预测.实验中,设置不同的网络结构和超参数,影响预测结果的准确性.通过对比,发现将Bi-LSTM-1神经元数设置为128,Bi-LSTM-2神经元数为128,Bi-LSTM-3神经元数为8,注意力机制层神经元数为64,全连接层神经元数为1时,此时模型预测精度最高.其次,迭代次数设置为1 500,Batch size为50,初始学习率为0.005,Adam作为优化器对模型参数进行更新优化,使用均方差做损失函数.此时,模型的RMSE最低. 首先,为验证本文基于Bi-LSTM-Att预测模型,划分出慢速退化期的预测方法相较于未划分状态预测方法的有效性,以轴承1作为验证集,轴承3、4、5和7作为训练集为例,RUL预测结果对比如图9所示.图中横坐标为采样时间(10 s),纵坐标为趋势性健康量化指标,蓝色线为实际RUL归一化值,橙色线为模型预测值.在轴承1的全寿命周期的第1 390采样点时,轴承1开始退化,反映在RMS曲线上呈现上升趋势.将这一时刻定义为轴承故障的起始时刻并开始预测轴承RUL.在2 714采样点时,轴承1状态发生剧烈变化,进入快速失效期.因此,1 390~2 714为轴承1的慢速退化期,充分利用了输入数据,避免了正常状态数据和失效数据对预测结果的干扰. 图9 基于Bi-LSTM-Att的滚动轴承1 RUL预测结果对比Fig.9 Comparison of rolling bearing1 RUL prediction results based on Bi-LSTM-Att 实验中,尽管在同一工况下使用型号相同的轴承,预测结果仍存在相差较大的退化趋势,同时数据量较少,因此在网络预测结果中不可避免地产生随机性和预测结果的波动.图9中,柱状图为各个时间点的预测误差值.通过对比(a)和(b)2幅误差柱状图可以看出,(a)中由于轴承处于健康阶段监测数据退化趋势不明显,这将导致RUL预测的波动性和不可靠性.与全寿命阶段的预测模型相比,进行状态划分的预测模型尽管预测值在前期波动性较大,但预测值在后期收敛在RUL真实值附近,能够较好地跟踪轴承退化趋势,可以提供更为准确的RUL预测结果且预测效果更为稳定.这充分验证了本文所提方法的有效性. 其次,为进一步验证本文选择Bi-LSTM-Att模型的优越性,引入对时间序列具有强大学习能力的5种网络模型,即RNN、GRU、LSTM以及不加注意力机制的Bi-LSTM.为了定量分析不同网络模型对轴承寿命预测效果的性能,本文采用2种评价指标,均方误差(root mean squared error,RMSE)和平均绝对百分比误差(mean absolute percentage error,MAPE)作为评估指标. RMSE表示预测误差的平方平均数,计算公式为 (28) MAPE表示各时间点相对误差的平均值,计算公式为 (29) 本次试验采用不同的时序预测模型进行对比,通过RMSE和MAPE进行评估.实验中为了消除随机性的影响,在模型选择最优的基础上,测试7组轴承,每次实验重复20次,最终以平均值作为测试结果,表3给出不同预测模型结果的量化指标. 表3 基于不同网络状态划分下的RUL预测结果对比Tab.3 Comparison of RUL prediction results based on different network state partitions 从上述实验结果中可以得到,对于5种考虑滚动轴承退化序列时序性质的网络模型,本文选用的Bi-LSTM-Att预测模型的RMSE和MAPE误差值均为最小.但由于网络的复杂程度加大,Bi-LSTM-Att模型的预测时间较长.相较于传统RNN、GRU和LSTM单向结构网络模型,Bi-LSTM和Bi-LSTM-Att预测方法充分考虑了输入时间序列的“未来”信息,可以有效提高预测结果准确性,因此其RMSE和MAPE较小.进一步,将注意力机制融入Bi-LSTM模型中,能够有效地提高对输入时间维度信息中有用特征的捕捉,增强网络模型的表征能力,因此得到了最低的预测误差,实现预测结果的进一步改善. 针对传统滚动轴承全寿命周期中RUL预测精度低的问题,提出一种基于Bi-LSTM-Att网络模型的RUL预测方法.在原始输入的大量数据中,选取对外部扰动敏感的RMS时域特征值进行状态划分.RMS经过平滑滤波去除噪声后,采取Mann-Kendall检验法进行趋势判别,从而确定出退化趋势的起始点.再结合归一化奇异值相关系数法,确定出慢速退化阶段的终止点.最后,基于Bi-LSTM-Att网络模型对确定出的滚动轴承慢速退化期进行RUL预测.经PHM2012数据集验证,相较于轴承全寿命周期的RUL预测,本文所提方法充分利用监测数据中的退化信息,能更好地挖掘滚动轴承的退化趋势;并且采用融合注意力机制的Bi-LSTM网络模型,进一步提高了RUL预测的准确性.
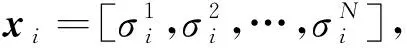
2 基于Bi-LSTM-Att网络的轴承RUL预测
2.1 Bi-LSTM-Att模型搭建

2.2 滚动轴承RUL预测

3 实验验证和结果分析
3.1 数据集介绍
3.2 数据预处理

3.3 慢速退化期确定




3.4 RUL预测

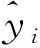

4 结 论
