基于梯度差自适应学习率优化的改进YOLOX目标检测算法

宋玉存，葛泉波，朱军龙，陆振宇

1．南京信息工程大学 人工智能学院（未来技术学院），南京 210044

2．南京信息工程大学 自动化学院，南京 210044

3．南京信息工程大学 江苏省大气环境与装备技术协同创新中心，南京 210044

4．南京信息工程大学 江苏省智能气象探测机器人工程研究中心，南京 210044

5．河南科技大学 信息工程学院，洛阳 471000

目标检测任务就是找出图像中所有感兴趣的目标物体，不仅要确定其类别，还要找到其在图像中的位置，因此目标检测一直以来都是计算机视觉的热门问题之一。由于深度学习的广泛运用，使得目标检测算法也由传统的目标检测算法发展为基于深度学习的目标检测算法［1］。基于深度学习的目标检测可分为2 类，分别为One-Stage 目标检测和Two-Stage 目标检测算法。Two-Stage 指的是检测算法需要分2 步完成，如R-CNN 系列［2-5］算法，首先需要获取待检测物体的候选区域，然后再进行分类；与之相对的是One-Stage 检测方法，可以理解为一步检测到位，且不需要单独寻找物体的候选区域，典型算法有SSD/YOLO［6-7］。这2 类算法在检测准确度和检测速度方面各有优势，但目前One-Stage 的目标检测算法的识别精度已经与Two-Stage 的识别精度不相上下，且One-Stage 的目标检测速度要快于Two-Stage 的目标检测，因此One-Stage 目标检测算法的研究是当前主流方向。

在One-Stage 的目标算法体系中，无论是在使用范围和影响力方面YOLO 系列算法都较为突出［8］。原始版本的YOLO 目标检测算法是2016 年提出的，它具有非常快的检测速度，但精度还有待提高［6］。同年提出的SSD［7］目标检测算法，相比于YOLOv1［6］进一步提高了检测的精度与速度。随后，众多学者针对YOLOv1 提出不同的改进算法，包括YOLOv2、YOLOv3、YOLOv4和YOLOv5 目标检测算法［9-12］。最新的版本是2021 年由旷视科技提出的YOLOX［13］目标检测算法，它将解耦头、无锚点以及标签分类等目标检测领域的优秀进展与YOLO 进行了巧妙的集成组合，不仅超越了已有的YOLO 的各个版本，而且在模型的推理速度上取得极大的突破。然而，在自然界中由于各类物体具有不同的外观、形状、大小和姿态，再加上物体成像时面临的光照、遮挡和视角等因素，这些都对目标检测的结果造成了巨大的影响，从而导致现实环境中现有的目标检测算法依然面临着巨大的挑战，并且如何提升目标检测的精度也成为了众多学者的研究热点［14］。

YOLOX 目标检测算法虽然在各方面的表现都很优异，但进一步提升和挖掘YOLOX 算法的性能同样也非常重要。新算法针对YOLOX 从3个不同的方向进行改进，分别是数据增强、网络结构和损失函数：① YOLOX 算法的数据增强会造成一部分图像色彩不均衡，从而必将影响网络的特征提取，因此采用随机增加亮度和对比度来解决该问题；② 网络结构是影响整个YOLOX 算法精度的重要环节，因此新算法也从激活函数和网络头结构进行改进，以进一步提升其网络模型的精度；③ 由于YOLOX 中所使用的损失函数并未解决目标检测算法中正负样本不均衡问题，新算法通过采用新的损失函数来应对。

在深度学习任务中，神经网络学习的过程需要使用优化算法进行神经网络参数学习，以使得网络损失函数的值尽可能小。一个好的神经网络优化算法可以使网络模型能够快速收敛，从而达到更好的性能表现［15］。深度神经网络的优化能力关系着网络最终的性能表现，但其神经网络数百千万的巨大参数量，使得网络参数的优化学习也异常困难。目前使用最广泛的深度学习优化算法包括随机梯度下降法［16］和一些自适应学习率的优化算法。相对于随机梯度下降法，自适应学习率算法则有更快的收敛速度和良好的泛化性能，因此如何设计出更好的自适应学习率的优化算法对提升神经网络的性能表现非常重要。

深度神经网络优化算法的研究一直都是众多学者研究的热点。通常根据优化算法在优化过程中使用的导数阶数可以将优化算法分为2 大类，分别是一阶优化算法和二阶优化算法［17］。其中二阶优化算法具有快速收敛的特点，但由于深度神经网络的巨大参数量，二阶优化算法的计算过程要求解二阶导数，导致二阶优化算法并不适用于深度神经网络的优化中，因此更多的是对一阶优化算法的研究［18］。一阶优化算法中以梯度下降法和自适应学习率的优化算法使用最为常见，其中自适应学习率的优化算法相比较梯度下降法具有更快的收敛速度，但是其自身泛化能力较差。最早的自适应学习率优化算法AdaGrad［19］于2011 年提出，之后又提出一些改进后的自适应学习率优化算法，如AdaDelta 算法［20］、RMSprop 算法［21］以及Adam 算法［22］。其中，Adam 算法自2015 年提出至今一直备受欢迎，且众多针对Adam 算法的改进自适应算法也层出不穷，包括AdaBound 算法［23］、DiffGrad 算法［24］、还有最近2 年的AdaBelief 算法［25］和DecGD 算法［26］等。因此设计出一个好的神经网络优化算法，并将其用在深度神经网络的训练中提升网络模型性能是极其有意义的，能有效提高神经网络算法的应用性能。

1 问题描述

1.1 YOLOX 的目标检测

YOLOX 目标检测算法是以YOLOv3_spp作为基准模型。该模型采用DarkNet53 作为骨干网络，使用了空间金字塔池化结构（SPP），并添加了EMA 权值更新、cosine 学习率机制和IoU 损失等策略［13］。YOLOX 通过对基准模型做了以下的改进以提升神经网络的检测精度和速度：① 在模型的输入端采用了更强的数据增强方法，对于基准模型的主干网络并没有做出修改，只在网络的预测头使用解耦头，这不仅提升网络的精度，也加快了网络的收敛速度；② 采用anchor free、multi postives 和SimOTA 等方法的共同作用使YOLOX 目标检测算法获得了优越的精度和极快的推理速度；③ YOLOX 又针对YOLOv5［12］的网络做出改进，包括改进了YOLOv5的主干网络、在YOLOv5 的Mosaic 数据增强方法后使用MixUp［27］数据增强方法、采用SiLU 激活函数［28］等方法。根据网络的大小和深度，对改进的网络命名为 YOLOX-S、YOLOX-M、YOLOX-L 和YOLOX-X，网络的大小越大深度越深，其网络的性能越好［13］。

1.2 神经网络优化

深度神经网络模型是一个高度非线性模型，其训练过程就是求得这个非线性模型的最优解，一般通过求解损失函数来得到。损失函数是一个非凸函数，在求得损失函数的最优点的过程中，可能会得到损失函数的局部最小值，从而不能使模型达到最好的性能。神经网络优化算法就是为了能够使得网络尽可能达到最优解，好的优化算法能够使网络模型快速收敛，同时使得模型有更好的泛化能力。

现有广泛用于神经网络的优化算法都是一阶优化算法，它需求得待优化目标的梯度，并使用一个学习率去控制优化算法一点点去接近最优点，因此优化算法学习率的选择则至关重要［17］。传统梯度下降法使用一个固定的学习率去一步一步得到最优点，但固定学习率会导致收敛速度过慢。自适应学习率的优化算法会在优化的过程中根据待优化参数的不同而分配不同的学习率，从而可以使优化算法快速收敛，所以如何设计一个更好的自适应学习率的策略就至关重要［15］。二阶优化算法的收敛速度极快，但是由于高昂的计算成本导致无法用于大规模的神经网络优化过程。众所周知，牛顿法就是二阶优化算法，其收敛速度快主要在于优化过程中需要计算待优化函数的二阶矩阵的逆，这里矩阵的逆可以看作是优化算法自适应的学习率［18］。另外，可以通过学习二阶优化算法自适应学习率的策略，应用于一阶优化算法中，以提升一阶优化算法的优化效果。

1.3 研究动机

为提升YOLOX［13］模型的收敛速度和精度，考虑对YOLOX 做出进一步改进，主要从数据增强、改变网络结构和网络的损失函数3 方面进行。同时，设计新的基于梯度差自适应学习率的优化算法并用于YOLOX 网络的训练任务，以此来进一步提升YOLOX 的模型精度。

1） 在YOLOX 的输入端使用随机增加对比度和亮度去解决原图像增强后图像色彩不均衡的问题。YOLOX 中使用MixUp［27］将经过Mosaic 处理过的图像再与随机一张裁剪过的图像按相同的权重直接相加融合，融合后的图片包含了2 张原图片各一半的信息，与原图片相比就失去了一半的色彩信息，这会导致增强后的图片色彩不均衡。针对这一问题，通过对数据增强后的图片使用随机增加对比度和亮度进行处理，使其增强后丢失色彩信息的图像随机增加一部分色彩，从而均衡数据增强后的图像。

2） 在YOLOX 网络的预测头中使用新的激活函数替代原有的SiLU 激活函数［28］来增强网络的预测能力。通过改进YOLOX 的预测头结构来提升网络的预测准确性，因此从预测头网络中的激活函数入手提出一种新的用于YOLOX 预测头的激活函数，命名为SoftTanh 激活函数。YOLOX 中使用的激活函数是SiLU 激活函数，SoftTanh 激活函数相对于SiLU 激活函数具有更稀疏的特性，更稀疏的激活函数可以使神经网络在训练时更容易收敛，可以进一步提升网络的精度。

3） 针对YOLOX 网络解耦头复杂的卷积结构，改进的方法对其解耦头重新解耦设计和优化，以提升解耦头部分的精度［13］。YOLOX 的网络解耦头首先是将分类和回归解耦成2 个分支，之后再将回归部分再解耦成2 个分支。新算法将分类和回归直接一步解耦为3 个分支，将原来回归的2 个分支解耦提前与分类分支解耦，这样的设计使得网络针对3 个解耦分支进行了同样深度和数量的卷积操作，相比原网络增加了2 个卷积层，进一步提升了网络的回归准确性。

4） 使用FocalLoss 函数［29］代替YOLOX 网络原有的BCEWithLogitsLoss 函数去解决网络分类中正负样本不均衡的问题。YOLOX 在计算目标损失使用的是BCEWithLogitsLoss 函数，该函数在目标检测中主要是用来进行样本的正负分类。但是在目标检测分类任务中，正样本的数量是要远小于负样本的数量，就造成了正负样本不均衡的问题，BCEWithLogitsLoss 函数对正负样本计算损失时是按相同权重计算，无法使网络更好的学习正样本。FocalLoss 函数针对正负样本赋予不同权重损失，使得模型训练时更专注正样本的分类，提升网络对正样本的分类效果，解决正负样本不均衡的问题。

5） 提出一种基于梯度差自适应学习率的新型优化算法，用于神经网络的训练以提升网络模型的性能表现。现有优化算法中二阶优化算法比一阶优化算法好，其主要是因为二阶优化算法需要计算待优化函数的二阶导数，二阶导数表示的是一阶导数的变化率，从函数图像上反应的是函数的凹凸性，这也意味着二阶优化算法考虑了待优化函数的曲率信息。现考虑用一阶梯度的差来表示待优化函数的曲率信息，以梯度差来作为学习率自适应的一个策略，同时引入梯度分解去代替原有的梯度信息，设计出基于梯度差自适应学习率的优化算法。

上述5 点共同改进YOLOX 目标检测算法，这5 点改进分别针对的是YOLOX 网络的数据增强、网络结构、损失函数和优化算法，相互之间的作用共同提升了YOLOX 的性能。

2 改进的YOLOX 目标检测算法

2.1 从数据增强方面改进YOLOX

在神经网络中经常需要对训练集使用数据增强方法，从而防止神经网络对训练集过拟合，同时数据增强也可以弥补训练数据不足，达到扩充数据集的目的。

2.1.1 YOLOX 的数据增强算法

YOLOX 在数据增强部分主要使用了Mosaic 和MixUp 数据增强算法。Mosaic 数据增强方法在YOLOv4［11］中提出，该算法是CutMix 数据增强方法的改进，Mosaic 数据增强通过随机选取4 张图像进行拼接成一张图片，以增加单张图片中的目标数量。对每张图像的目标位置，拼接后图像中目标位置相对于原未拼接的图像中目标的位置需要重新计算，Mosaic 的增强效果如图1 所示［29］。

图1 Mosaic 数据增强效果图［29］Fig.1 Mosaic data enhancement picture［29］

通过Mosaic 数据增强后，YOLOX 再使用MixUp 数据增强方法。MixUp 数据增强［27］可以提升网络模型的泛化能力，该算法是将随机2 张图片按不同的权重进行融合从而生成一张新的图像，对于图片的标签也按照同样的权重进行融合生成新的标签，相对应的计算公式为［27］

式中：λ∈[0，1]；xi，j、yi，j分别表示随机选取的2 张图片和相对应图像的标签。在目标检测中λ一般取值0.5，这样对于计算损失函数时可以不用考虑数据标签。YOLOX 是将Mosaic 数据增强后的图片和随机选取的一张图片进行MixUp 数据增强，图片的融合效果如图2 所示［30］。

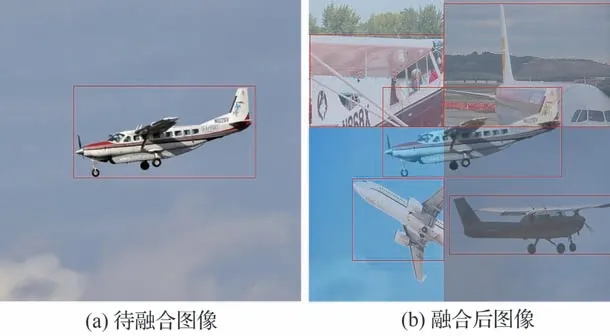
图2 MixUp 数据增强效果图［30］Fig.2 MixUp data enhancement picture［30］

图2 （a）为随机选取的待融合的图像，图2（b）为MixUp 将待融合的图像和经过Mosaic 数据增强［11］后的图像融合的结果，通过加权融合后的图像包含了更多待检测的目标，但是也让图像丢失了一部分色彩信息。为了进一步增强模型的泛化能力和鲁棒性，对融合后的数据采取进一步的数据增强，使增强后的图像恢复一部分色彩信息。

2.1.2 改进YOLOX 的数据增强算法

改进YOLOX 的数据增强算法是在原有数据增强算法后再使用随机改变图像的对比度和亮度的数据增强算法，通过随机对图像像素加减某个值来改变图像的亮度和随机对图像像素乘某个值来改变图像的对比度，即

式中：xiω表示改变图像对比度，增加的ψ表示亮度的变化，ω∈[1，2]，ψ∈[-10，10]为随机值以达到对每张图像数据随机改变图像的对比度和亮度的效果。同时为了防止增强后的图像数据出现像素值过小或者像素值溢出，需要对增强后的数据进一步处理，对增强后像素值＜0 的像素点置0，对于增强后的像素值＞255 的像素点设置为255，这样便改变了增强后图像的对比度和亮度。将随机改变图像的对比度和亮度的数据增强算法用在YOLOX 数据增强算法之后，使融合后的图像恢复一部分色彩信息，以提升网络模型的特征提取效果。

2.2 从网络结构方面改进YOLOX

在神经网络的网络结构中要使用激活函数，使用不同的激活函数就会有不同的网络结构，不同的激活函数对网络模型的影响也不同。一般激活函数都是非线性的，这样可以为网络模型加入非线性因素，因为线性模型的表达能力有限，好的激活函数能使网络的性能得到很大的提升。

2.2.1 YOLOX 中的激活函数

YOLOX 将YOLOv5［12］网络中使用的所有激活函数都改进为SiLU 激活函数［28］，该激活函数在深度模型上要优于传统ReLU 激活函数［31］，具有光滑、非单调、无上界和有下界的特点。

2.2.2 改进YOLOX 中的激活函数

为进一步提升YOLOX 网络的性能表现，针对YOLOX 的网络结构做出改进，提出了新的激活函数去替代YOLOX 检测头的激活函数，新的激活函数相比于其他激活函数具有更平滑的激活函数特性，更平滑的激活函数特性具有更好的泛化能力和有效的优化能力，可以进一步提高网络模型质量。

新的激活函数为式（7），命名为SoftTanh 激活函数，使用SoftTanh 激活函数替代YOLOX 网络预测头的SiLU 激活函数［28］，以提升YOLOX目标检测算法预测头的精度，ReLU［31］、SoftTanh和SiLU 激活函数图像如图3 所示。SoftTanh 激活函数在整个区间都具有良好的特性。

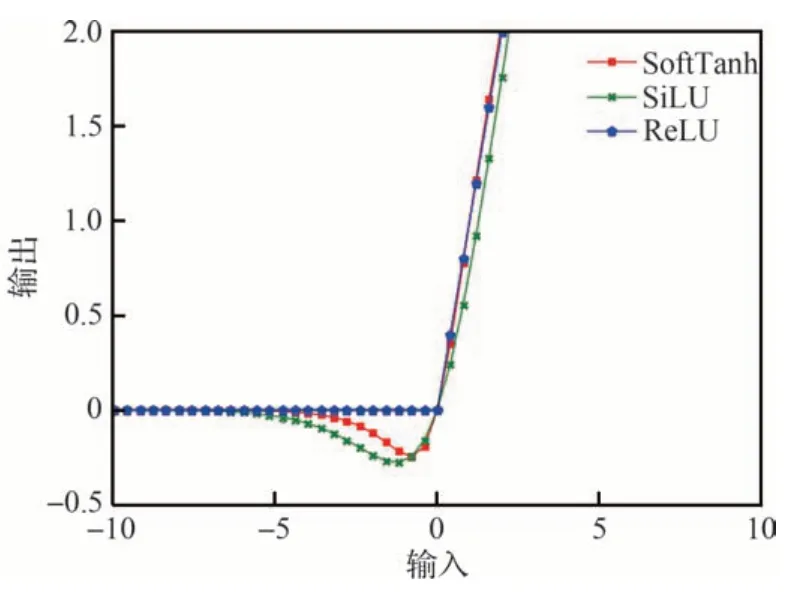
图3 激活函数的图像Fig.3 Image of activation function

1） SoftTanh 函数在＞0 的区间保持了ReLU激活函数良好的线性特性。从激活函数的图像可以看到SoftTanh 函数在输入＞0 的区间保留了与ReLU 激活函数相同的特性，从函数图像表现为ReLU 激活函数图像与SoftTanh 函数基本重合，这一点相比于SiLU 激活函数更好。

2） SoftTanh 函数在＜0 的区间具有更强的稀疏性，可以加快网络的计算。在＜0 的区间保留了一定的负值，这样弥补了ReLU 激活函数＜0 时激活值为0、梯度为0 的缺陷，与SiLU 激活函数相比较，当x→-∞时，SoftTanh 激活函数更快地趋近于0，这一点可以从图3 的函数曲线图看到。除此之外，通过求当x→-∞时，求SoftTanh 激活函数和SiLU 激活函数之商的极限来判断2 个激活函数谁更快地趋近于0，通过计算可以证明SoftTanh 激活函数在负区间更快趋近于0，那么给定的输入激活后的值就为0，在神经网络中就表示激活的矩阵中包含很多0，矩阵中更多的0 就意味着网络模型是稀疏的，稀疏网络因为要计算的东西更少，网络的计算速度也更快［31］。

将3 种激活函数应用到8 层随机初始化的全连接神经网络中，输入单张图像并对神经网络的输出进行可视化处理，其图像如图4 所示，依次是输入图像，使用ReLU、SiLU 和SoftTanh 激活函数的8 层全连接神经网络输出图像。从图4 可以看到，与SoftTanh 输出的平滑轮廓相比，ReLU的输出特征图有许多直接的过渡。SoftTanh 的输出同样要比SiLU 的输出更加平滑，更平滑的输出意味着平滑的损失，从而具有更容易的优化和更好的泛化特性。

图4 3 种激活函数在8 层随机初始化神经网络的输入输出图像Fig.4 Three activation functions randomly initializing input and output images of neural network in eight layers

2.2.3 改进YOLOX 中的解耦头

传统的YOLO 算法的检测头通常是直接通过分类和回归分支融合共享来实现的，YOLOX中网络检测头通过对融合特征的解耦来实现分类和回归，这种解耦的设计不仅仅在精度上有所提高，而且也加快了YOLOX 网络的收敛速度［13］。针对YOLOX 网络的解耦头设计，将检测头进一步解耦，原YOLOX 解耦头的设计和改进YOLOX 解耦头的设计如图5 所示。YOLOX 的网络解耦头是将分类和回归解耦成2 个分支，之后再将回归部分再解耦成2 个分支。新算法将分类和回归直接一步解耦为3 个分支，将原来回归的2 个分支提前解耦与分类解耦，这样的设计使得网络针对3 个解耦分支进行了同样深度和数量的卷积操作，比原网络增加了2 个卷积层，相应的因为卷积层数的增加，整个网络的参数量和计算量也都有所增加，通过计算可以得到YOLOX-S 和改进后YOLOX-S 的参数量和运算量。

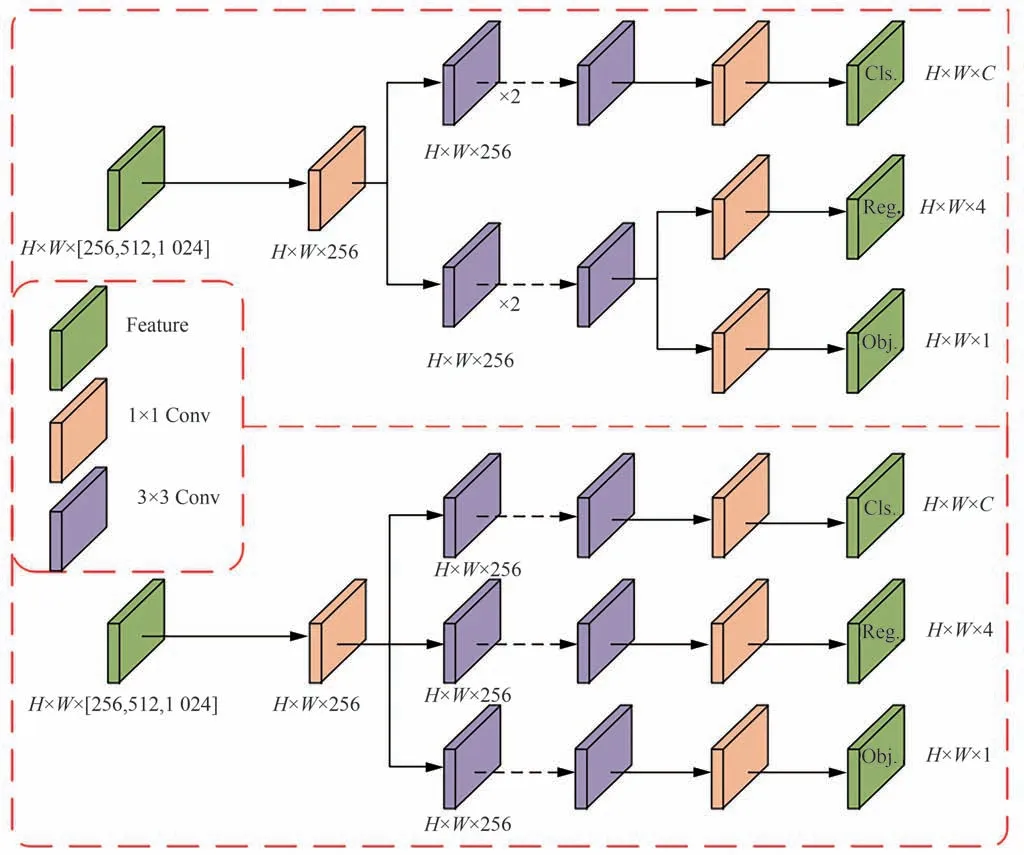
图5 改进YOLOX 解耦头Fig.5 Improved YOLOX decoupled head

从表1 可以看到增加卷积层后的YOLOX-S相比于原网络参数量增加了10.1%，相应的运算量增加了17.6%。虽然整个网络的参数量和运算量有所增加，但通过实验可以发现增加卷积层的YOLOX-S 与原网络相比，网络回归的准确性得到了提升，可以从图6［32］看到。

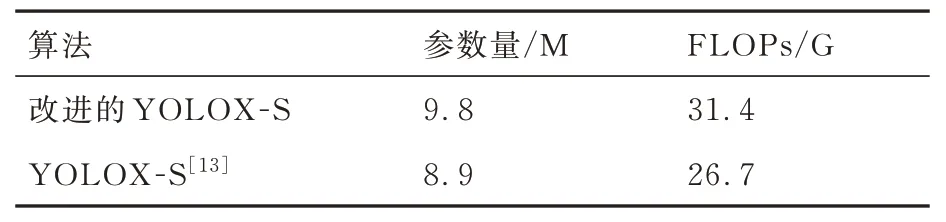
表1 改进的YOLOX-S 的参数量和运算量Table 1 Improved YOLOX-S parameters and FLOPs

图6 原网络与增加卷积层的YOLOX-S目标检测效果图［32］Fig.6 YOLOX-S object detection results of original network and added convolutional layer［32］

图6 中左图为原YOLOX-S 目标检测结果，右图为增加2 层卷积后的目标检测结果，可以看到图中右上角的立交桥在原YOLOX-S 网络中并未被检测到，增加卷积层后的YOLOX-S 网络回归准确性得到了提升，位于右上角的立交桥也被检测到。因此，对YOLOX 的解耦头进一步解耦，虽然网络参数和运算都有所增加，但对于提升网络回归准确性也具有明显效果。

2.3 改进YOLOX 的损失函数

损失函数是用来评估模型的预测值与真实值之间的差值，在深度学习的训练过程中，往往需要通过使损失函数最小化，从而使得训练的模型能够收敛，选择一个好的损失函数可以使得模型具有更好的性能表现。

2.3.1 YOLOX 中的损失函数

YOLOX 网络的损失函数包括3 部分，分别是IoU 损失，类别损失和目标损失［13］。IoU 损失的作用是通过计算预测目标框与真实目地之间的交并比来使得网络能够更加准确地预测出目标框的位置信息；类别损失是计算目标类别的真实值与预测值之间的损失；目标损失的作用是通过判断当前预测候选框是目标还是背景，进一步使网络能更加准确地将目标与背景分开。在YOLOX 的网络中，类别损失和目标损失都使用了BCEWithLogitsLoss 函数［29］，该函数是对输入的数据先使用Sigmoid 函数（8），之后使用BCELoss 函数，常用于多标签分类任务。

2.3.2 改进YOLOX 中的损失函数

在目标检测中One-Stage 目标检测的检测精度要低于Two-Stage 目标检测，主要因为样本类别不均衡造成正负样本难分类，解决的方法通常是使用FocalLoss 函数［29］。该函数是在交叉熵函数上做改进，交叉熵损失函数在计算损失时，每个样本使用相同的权重。在目标检测中，正样本是检测的目标，负样本是大量的背景，正负样本在数量上有着非常大的差距，但使用交叉熵损失函数并不能使模型能更好地区分正负样本，FocallLoss 函数针对正负样本不均衡，分别赋予不同的权重，对于正样本因为数量少，需要设置更大的权重，相反，对于负样本设置较小的权重。对于正负样本难分类的问题，通过一个调制系数，对容易分类的样本减小其权重，对难以分类的样本增大其权重，计算公式为［29］

式中：σ是根据正负样本的比例来决定的，σ∈(0，1)，将σ设置为FocalLoss 论文默认取值0.25，（当σ设置为0.25 时改进的YOLOX-S 算法在RSOD［32］数据集中的性能并非最好）。对此分别设置参数σ=0.1，0.2，0.3，实验发现当参数σ=0.2 时，改进的YOLOX-S 在RSOD 数据集中的结果更好。式（9）中pt表示检测的结果，其值的范围是［0，1］，该值越大表示可信度越高，越容易分类样本，相反，值越小可信度越小，更难分类。γ是一个调制系数，可以控制容易分类和更难分类样本的权重，γ∈(0，5)，文中默认取值为2。当pt越大表示越容易分类，则(1-pt)2也就更小，损失函数的值也就越小。当pt越小表示越难分类，则(1-pt)2也就更大，损失就更大，损失变大会使神经网络更倾向于更难分类样本参数的学习，从而提升神经网络对难分类样本的分类准确性。

3 算法介绍

3.1 自适应学习率的优化算法

自适应学习率的优化算法框架都是基于梯度下降法改进的，区别在于两者学习率的设置不同。在随机梯度下降算法［16］中，针对每个待优化的参数学习率α是一致的，算法迭代公式为

式中：θ是待优化的参数；gt表示待优化函数的梯度，通常在使用随机梯度下降法时更普遍使用带动量项的随机梯度下降法［33］，即

式中：mt为动量项，通过指数加权平均包含了过去梯度的信息，可以使梯度下降的方向基于过去累计梯度的方向。自适应学习率优化算法的学习率是针对不同参数有不同的学习率，最早的自适应学习率优化算法AdaGrad［19］是通过积累过去梯度的平方和的根来实现自适应学习率，即

式中：Gt是过去t次迭代梯度的和；ε是为了保持分母数值稳定的常数，默认取值为10-10。之后就出现了各种自适应学习率优化算法，其中使用最为广泛的就是Adam 算法［22］，它结合了AdaGrad［19］和RMSProp 算法［21］的优点，根据梯度的第一和第二矩的估计计算不同参数的各个自适应学习率，即

式中：mt表示梯度gt的指数加权移动平均值，为梯度的一阶矩估计，用来控制模型更新的方向；β1是指数加权移动平均的衰减率，默认取值为0.9；vt表示梯度g2t的指数加权移动平均值，为梯度的二阶矩估计，用来控制学习率；β2为指数加权移动平均的衰减率，默认的取值为0.999；m̂t和v̂t是对mt和vt进行偏差修正；ε是为了保持分母数值稳定的常数，默认取值为10-8。AdaBelief 算法［25］针对Adam 算法做出了改进，使用(gt-mt)2来代替式（16）中的g2t，使得算法在更新时方差大减小学习率，方差小增大学习率，即

式中：β1、β2和ε的默认取值与Adam 算法中β1、β2和ε的取值相同，分别为0.9、0.999 和10-8。自适应学习率的优化算法需要根据过去迭代的梯度信息来实现学习率的自适应，如何利用过去迭代的梯度信息设计出更好的自适应学习率策略非常关键，DecGD 算法中提出使用损失来实现学习率的自适应，在网络学习的过程中，学习率的大小应该随着函数的损失减小而减小，该算法利用复合函数

来表示损失函数，其中c默认为1，然后对复合函数求导将梯度进行分解为复合函数和复合函数导数的乘积得到

其中：复合函数的导数为

复合函数则使用一元泰勒展开来近似表达，其中复合函数的近似为

最后使用2g(x)∇g(x)来表示原梯度来实现梯度下降。

新提出的优化算法是基于梯度差的信息来实现学习率的自适应，同时结合了DecGD 方法的梯度分解，使用复合函数来表示原损失函数，相比较于现有方法，具有更好的学习率自适应性。

3.2 基于梯度差自适应学习率的优化算法

f(θ)是一个待优化的函数，其函数图像如图7 所示，要求得f(θ)的极小值，可使用随机梯度下降法迭代法，但是在随机梯度下降法中的学习率大小不变，固定的学习率会导致算法在最优点来回震荡，难以达到最优点。

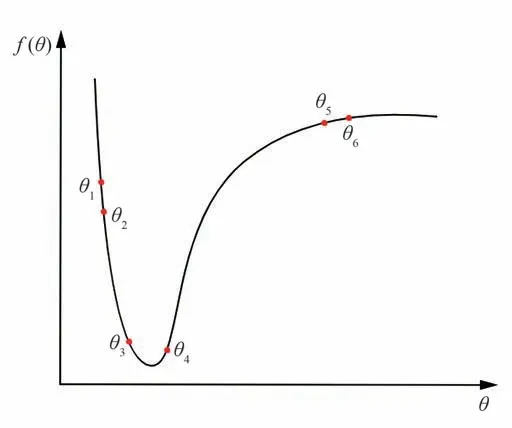
图7 f (θ)函数图像Fig.7 f (θ) functional image

基于梯度差的自适应学习率使用梯度差信息来表示待优化函数的曲率信息，以曲率值的大小来控制学习率的变化，设计出一个基于梯度差自适应学习率的优化算法。在图7 中，点θ3和θ4在最优点附近，学习率应该设置的较小，这样可以避免算法迭代在最优点震荡，在最优点之外，点θ1和θ2或点θ5和θ6处学习率可以设置较大一点，这样可以使算法快速迭代到最优点附近。最优点附近的梯度差|g(θ4)-g(θ3)|要大于最优点之外的梯度差|g(θ2)-g(θ1)|和|g(θ6)-g(θ5)|，因此可以利用梯度差信息来控制学习率在算法迭代过程中的大小。在最优点附近，梯度差大，学习率小；在最优点之外，梯度差小，学习率大，学习率的大小与梯度差成反比。

式中：Δgt为梯度差，表示当前梯度gt与过去梯度gt-1的差值，使用梯度差作为学习率自适应的一个策略，这个差值可以反应出待优化函数的曲率变化信息，通过曲率信息的变化自动调整学习率的大小，从而实现学习率的自适应。当前梯度与上一步迭代的梯度的差值可能为正值，也可能为负值，差值的正负表示曲线向上弯曲还是向下弯曲，与梯度下降的方向没有关系，因此可以只考虑差值的大小。

现考虑将基于梯度差自适应的策略与梯度分解进行结合，以实现更好的自适应学习策略。这里使用对数函数（26）作为损失函数的复合函数，损失函数f(θt)是一个恒大于零的函数，当损失为零时，复合函数h(θt)=ln (f(θt)+1)也为零，对复合函数求导，得到梯度∇h(θt)，对复合函数的梯度引入动量加速法得到，复合函数的本身使用一元泰勒公式近似为式（30）。算法的更新规则是使用当前梯度近似值mtevt和当前梯度gt的不同权重结合替换传统梯度下降法的梯度，同时引入当前的梯度差，以实现基于梯度差自适应学习率的神经网络优化算法。

式中：mt表示复合函数的梯度∇h(θt) 的指数加权移动平均值，参数β1表示指数加权移动平均衰减率，默认取值0.9。α表示学习率，默认为0.01，参数ε既可以防止梯度差作为分母为零，也可以针对不同的优化任务进行适当的参数调整，默认为0.01。β2作为当前梯度和当前梯度近似梯度融合的权重，β2∈(0，1)，默认取值0.3。

通过使用基于梯度差自适应学习率的优化算法去优化高维的非凸函数，并对其自适应学习优化算法的优化过程以及优化结果进行可视化，以重点分析其自适应学习算法的优化效果。选用Rastrigin 函数进行优化，Rastrigin 函数是一种典型的非凸函数，函数图像如图8 所示。

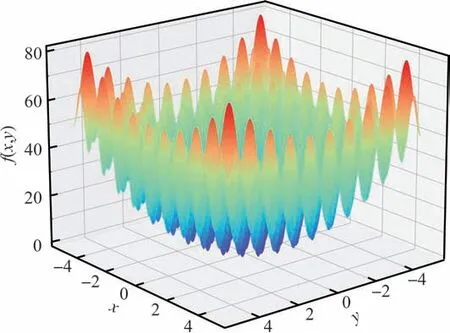
图8 Rastrigin 函数图像Fig.8 Rastrigin functional image

Rastrigin 函数表达式为

式中：A和n通常设为10 和2，当x=0 时，有全局最优点f(0)=0。分别采用不同的优化算法针对Rastrigin 函数进行200 次迭代优化并对其优化过程以及优化结果可视化处理。不同优化算法的优化效果如图9 所示。因为Rastrigin 函数具有多个局部的极大值点和极小值点，其最优点在（0，0），常规的优化算法很容易陷入局部最优点，图9中的SGDM、Adam 以及AdaBelief 算法在经过200 次迭代过程中都陷入了局部最优点，本文优化算法在200 次迭代中经过局部最优点最终迭代得到全局最优点（0， 0）。

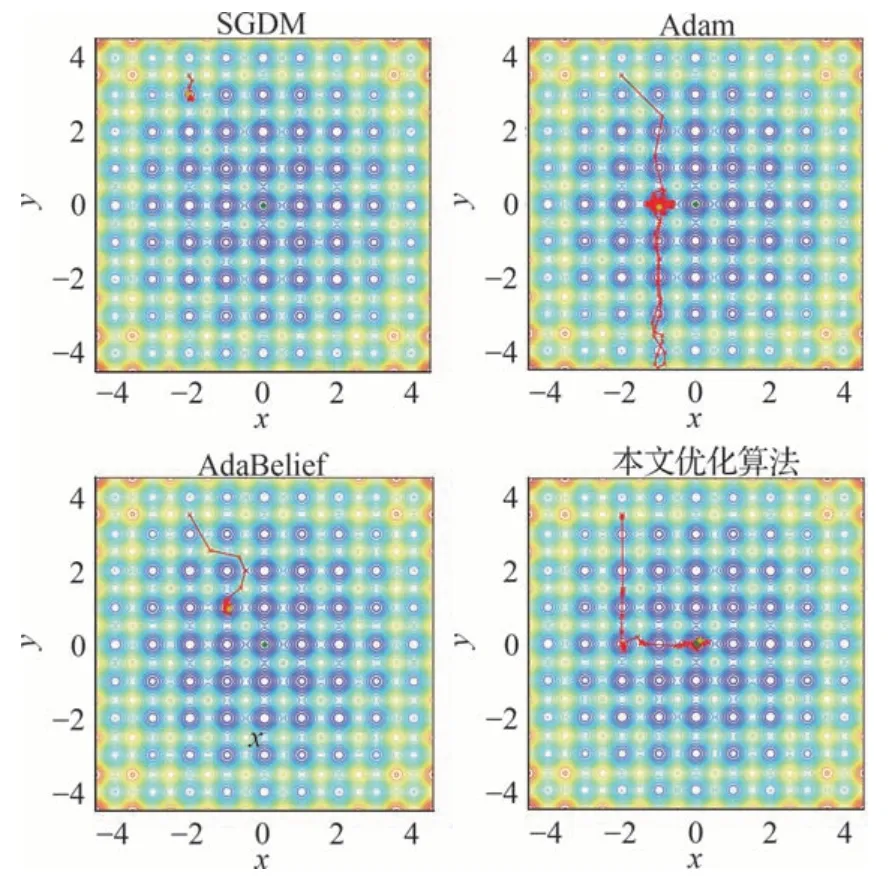
图9 不同优化算法在Rastrigin 函数迭代优化效果图Fig.9 Rastrigin function iterative optimization results with different optimization algorithms

4 算法分析

针对最新的YOLOX 目标检测方法主要从数据增强、网络结构和网络损失函数3 个不同的方面做出改进，这些改进算法共同作用提升了其目标检测的性能。同时设计出一种新的基于梯度差自适应学习率的优化算法，将该优化算法用于训练改进过的YOLOX 目标检测任务，进一步提升目标检测的精度，并且该优化算法也可以用在其他神经网络的训练任务中去。

4.1 改进YOLOX 目标检测算法的耦合性

改进的YOLOX 目标检测算法从数据增强、网络结构和损失函数3 个不同方面进行改进，其中还有用于训练改进YOLOX-S 的基于梯度差的优化算法。

改进的数据增强方法是作用在输入网络的数据，式（3）是对原始数据增强后的图像进一步增强，恢复图像部分色彩信息，再将其输入到神经网络中，数据增强作用的是数据集，数据集与神经网络是2 个不同的模块，因此数据增强与神经网络的结构是非直接耦合关系。改进的损失函数是为了解决数据集正负样本不均衡的问题，但是数据增强与数据集的正负样本并没有直接关系，因此数据增强与改进损失函数之间也是非直接耦合关系。

改变网络结构影响的是网络的输出，通过改变网络的激活函数和改进网络的解耦头设计来改进网络的部分结构，使得网络具有更好的预测能力。改进的损失函数作用在网络学习分类的能力，式（9）中的损失函数可以对正负样本设置不同的权重，使网络对正负样本具有更强的分类能力。2 个方法分别作用在YOLOX-S 的不同方面，因此是非直接耦合的关系。用于训练改进YOLOX-S 的基于梯度差的优化算法单独作用于神经网络，因此基于梯度差的优化算法与改进YOLOX-S 算法之间不存在耦合关系。

同样可以通过实验仿真来验证各改进算法之间的耦合关系，针对不同的改进算法可以通过分步验证，依次验证单个改进算法是否有效。

4.2 基于梯度差自适应学习率的优化算法

使用梯度差的信息作为自适学习率的策略，同时将梯度分解的近似梯度去代替原损失函数的梯度信息，最后在算法的更新上使用了当前梯度和近似梯度的不同权重进行更新，梯度差自适应学习率的优化算法的详细信息如算法1 所示。其中：f(θ)∈R ，∀θ∈Rd，f为最小化的损失函数，θ为属于Rd的参数；t表示迭代次数；h(θt)=ln (f(θt)+1)；gt=∇f(θt)表示f(θt)的梯度；Δgt表示梯度差信息；α表示学习率，默认为10-3；ε为为防止梯度差作为分母为零设置的参数，默认为10-2；β1、β2表示平滑参数，分别设置为0.9和0.3。

?

基于梯度差自适应学习率的优化算法结合了梯度分解和梯度差信息作为自适应学习率调整的策略。AdaBelief［25］优化算法中使用移动指数加权平均的算法来计算当前梯度与当前梯度动量项的差来作为学习率自适应变化的计算算法，计算公式见式（20）。新算法直接使用了当前梯度与上一次迭代的梯度的差作为梯度信息的变化，以实现学习率的自适应。相比于AdaBelief算法，这样的计算方法更加简单和更易于理解。

DecGD［26］优化算法中将损失函数的梯度分解为2 项的乘积，这2 项通过使用损失函数的复合函数来引入。新算法使用了相似的方法，但是使用了不同的复合函数来表示损失函数。DecGD 优化算法使用表示损失函数的复合函数，当损失函数f(x)趋近于零时，复合函数g(x)只会无限趋近于c，因此复合函数g(x)不具有与损失函数f(x)相同的极限，无法与损失函数f(x)的变化做到同步。使用对数函数h(x)=ln (f(x)+1)作为损失函数的复合函数，当损失函数f(x)趋近于零时，复合函数h(x)与损失函数f(x)具有相同的极限，因此h(x)更能表达损失函数。通过梯度融合以达到梯度的近似性，从而使梯度更新的模型具有泛化性。

4.3 收敛性分析

使用在线学习框架分析基于梯度差自适应学习率的优化算法在凸情况下的收敛性，使用遗憾来评估优化算法，即在线预测ft(θt)和在最优点ft(θ*)之间的所有之前差异的总和，遗憾定义为

在线凸优化的标准假设如下：

假设1①X⊆Rd是紧凸集；②ft是凸的下半连续函数，其中gt=∂ft(θt)；③D=maxθ，λ∈X||θλ||∞，G=maxt||gt||∞。

根据假设1 可以提出以下引理：

引理1假设函数ft是有界的凸函数，对∀θ∈Rd，令ht(θ)=ln (ft(θ)+1)。如果ft具有有界的梯度，那么ht也具有有界梯度，并且在可行区域内有界，证明过程参考AdaBelief［25］算法。

根据假设1 和引理1，得出假设2。

假设2①X⊆Rd是紧凸集；②ft是凸下半连续的函数，ht=ln (ft+1)，其中lt=∂ht(θt)；③||θ-λ||≤D，||lt||≤H，||gt-gt||≤G，|exp(ht(θt))|≤L。

定理1设{θt}、{st}和{vt}为算法1 得到的序列，对∀t∈[T]，有0 ≤β1t≤β1＜1，0 ≤β2＜1，β11=β1，αt=，st-1≤st，0 ＜c≤。θ*表示域内的最优点，对由基于梯度差自适应学习率的优化算法生成的任意θt，有以下遗憾界，参考AdaBelief［25］优化算法的收敛证明思路可得：

推论1设β1，t=β1λt，0 ＜λ＜1，有：

推论2在定理1 相同假设情况下，算法1 对所有的T≥1，可得算法的平均遗憾收敛：

5 仿真实验

进行实验验证改进后的YOLOX-S 目标检测算法在不同数据集的表现，以及与其他目标检测算法在相同数据集上的比较，同时也将梯度差自适应学习率的优化算法与其他优化算法在不同神经网络上使用相同的数据集进行实验比较。

5.1 改进后的YOLOX-S 目标检测算法实验

实验验证改进后的YOLOX-S 目标检测算法的表现，首先在标准的PASCAL VOC 07+12数据集［30］进行实验，使用的是PASCAL VOC 07+12 的评价标准，实验设备使用的是NVIDIA A4000 显卡。用未改进的YOLOX-S 网络［13］进行实验得到一个基准的实验结果，之后依次使用FocalLoss 函数、数据增强算法、SoftTanh 激活函数以及解耦头去改进YOLOX-S 并进行实验对比，验证改进的方法对YOLOX-S 的作用，最后再使用基于梯度差自适应学习率的优化算法去替换原YOLOX-S 训练所使用的随机梯度下降法去训练改进的YOLOX-S 网络。

实验采用的评价指标是平均精度AP，从表2实验结果可以看出，使用FocalLoss 函数后，YOLOX-S 的AP 提升了1.02%，主要是因为FocalLoss 函数解决了目标检测任务中正负样本数据不均衡的问题，数据增强、新的激活函数和解耦头结构分别从数据和网络结构方面改进，分别从不同程度上提升了YOLOX-S 的AP。使用基于梯度差自适应学习率的优化算法使YOLOX-S 模型进一步优化，提升了YOLOX-S 的AP。改进后的YOLXO-S 算法的AP 相比较于未改进的YOLXO-S 算法的AP 提升明显，虽然各改进算法在精度方面对YOLOX-S 的提升效果大小各异，但总体上共同提升了算法的AP 表现。

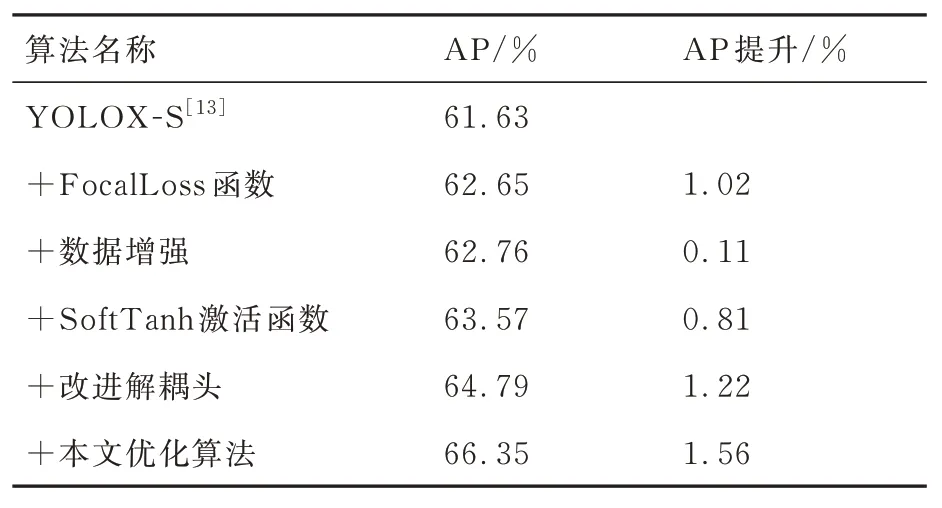
表2 改进的YOLOX-S 在VOC 数据集的实验结果Table 2 Experimental results of improved YOLOX-S in VOC datasets

使用相同的设备用改进后的YOLOX-S 算法与YOLOv3［10］算法、YOLOv5s［12］、未改进的YOLOX-S［13］算法以及最新由美团开源的YOLOv6s［34］算法在RSOD［32］数据集上进行实验比较，RSOD 数据集用于遥感图像中的物体检测，其包含飞机、操场、立交桥和油桶4 类目标共976张卫星图像，按照8∶2 随机划分为训练集和验证集进行实验，实验使用COCO 评估标准，不同目标检测算法在ROSD 数据集的实验结果如表3所示。

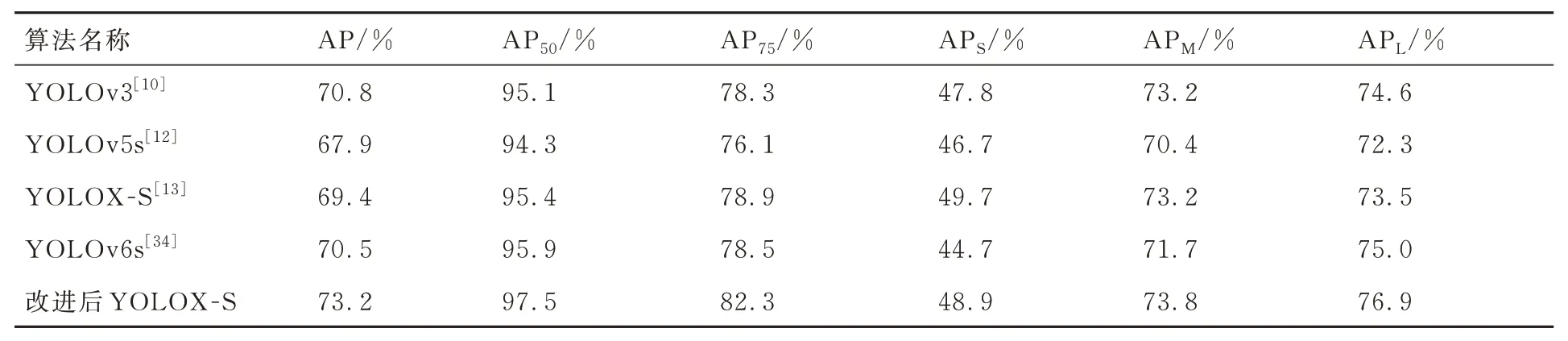
表3 不同目标检测算法在RSOD 的实验结果Table 3 Experimental results of different object detection algorithms in RSOD

从表3 可以看到改进后的YOLOX-S 算法在RSOD 数据集的不同评价指标都有提升，这也表明了，通过对YOLOX-S 从数据增强、激活函数、网络结构和优化算法方面的改进针对不同的数据集也可提升AP。其中AP50和AP75是算法预测框与真实框IOU＞0.5 和0.75 的平均精度，IOU 越大预测的越准确，APS、APM和APL分别表示不同大小目标的平均精度，S、M 和L 分别表示小、中和大目标。在表3 的实验结果可以看到改进后的YOLOX-S 在RSOD 数据集上的实验结果的大部分指标都要优于其他算法，其中AP50和AP75的实验结果比原YOLOX-S 的实验结果分别提升了1.5%和3.1%，精度提升效果明显。改进后的YOLOX-S 在RSOD 数据集上APM和APL的实验结果要优于原YOLOX-S，其中改进后的YOLOX-S 的大目标检测中的精度提升明显，其平均精度提升了2.8%。而且改进后的YOLOX 算法与最新的YOLOv6-s 目标检测算法相比较，在各项评价指标中都有更好的表现。

通过对RSOD 验证集的目标检测结果可视化后，可以发现改进后的YOLOX-S 相比于原算法的具体优势在于可以降低图像中目标的漏检和误检问题，具体的情形如图10［32］所示。对于图10（a）中的2 个操场只检测到一个，图10（b）中2 个操场都检测到，改进后的YOLOX-S 降低了图像中目标的漏检。图10（c）中，原YOLOX-S目标检测结果误将类似飞机形状的草坪检测为飞机，图10（d）为改进后的YOLOX-S 的目标检测结果，很明显改进后的YOLOX-S 可以减低目标的误检。

图10 原算法（左）与改进后算法（右）目标检测结果图［32］Fig.10 Object detection result of original（left）， and improved algorithm（right）［32］

5.2 梯度差优化算法的性能验证实验

为验证新的优化算法的优化效果，使用相同的实验设备，分别使用SGDM［16］、Adam［22］、Ada-Belief［25］优化算法以及梯度差优化算法在RSOD数据集训练改进后的YOLOX-S 网络，其中各优化器的参数设置都为默认参数，实验结果如表4所示

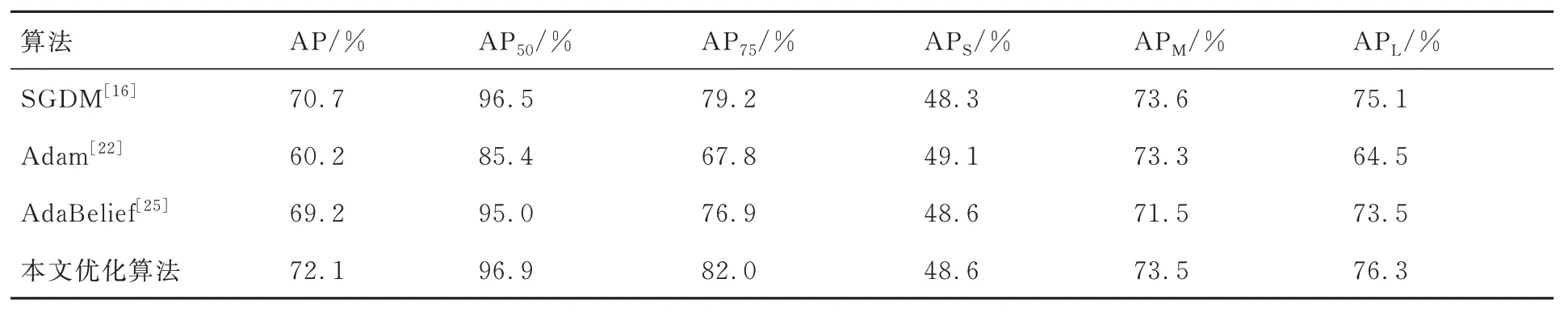
表4 相同网络不同优化算法的实验结果Table 4 Experimental results of the same network and different optimization algorithms

从表4的实验结果可以看到，在使用RSOD 数据集和相同的网络模型条件下，梯度差自适应学习率的优化算法较其他优化算法在AP 上有一定的提升，这也表明基于梯度差自适应学习率的优化算法具有更好的优化效果。采用SGDM 训练改进后的YOLOX-S 算法相较于Adam 和AdaBelief 算法有一定的优势，但是与基于梯度差自适应优化算法训练改进后的YOLOX-S 网络相比较，基于梯度差自适应优化算法具有更好的AP 提升。

为验证基于梯度差自适应学习率的优化算法在其他神经网络的优化结果，使用该优化算法与其他主流的优化算法在图像分类任务上进行实验比较。在图像分类任务中使用CIFAR10 数据集［35］，分别使用VGG11［36］、ResNet34［37］和DenseNet121［38］经典网络进行实验，其中各优化器的参数都为默认参数，实验结果如图11 所示。

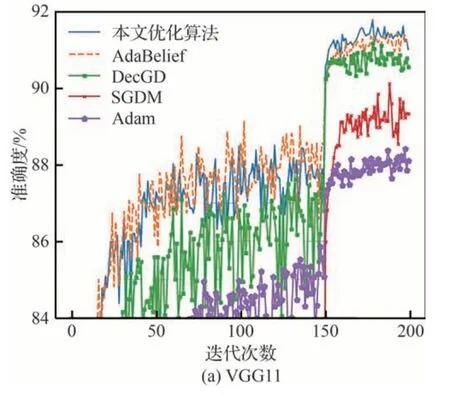
图11 CIFAR10 数 据 集 在 VGG11、ResNet34 和DenseNet121 的精度曲线Fig.11 Accuracy curves of CIFAR10 datasets in VGG11， ResNet34 and DenseNet121

从图11 的精度曲线可以看到不同优化算法在CIFAR10 数据集和各图像分类网络模型的条件下，本文优化算法都具有更好的优化表现，这也表明本文优化算法在不同神经网络中的优化都是有效的。本文优化算法在VGG11 网络中的表现要明显优于其他优化算法，在ResNet34 网络中本文的优化算法也要优于SGDM 和Adam优化算法，与AdaBelief 优化算法的表现不相上下，在DenseNet121 网络中本文的优化算法的表现也优于SGDM 和Adam 优化算法，与AdaBeief优化算法相比效果也要好一点。

6 结 论

本文针对最新的YOLOX 目标检测算法从3方面做出改进，设计出基于梯度差自适应学习率的优化算法用于改进后的YOLOX 网络的训练任务，并通过实验验证了改进后的YOLOX-S 在不同数据集的表现要优于原YOLOX-S 算法。同时将基于梯度差自适应学习率的神经网络优化算法用于其他神经网络的训练任务，并在不同任务中进行实验，实验验证了基于梯度差自适应学习率优化算法的优化表现要优于现有的优化算法，最后对本文提出的优化算法做出了收敛性证明。未来将会在不同大小尺寸的YOLOX 网络上进行改进，使用更大的数据集进行实验，并将改进的算法应用到实际的目标检测任务中去。