基于改进L-SHADE 算法的航空发动机性能退化评估

2023-08-31秦海勤赵杰任立坤李边疆

航空学报 2023年14期

秦海勤，赵杰，任立坤，李边疆

海军航空大学青岛校区力学工程系，青岛 266000

航空发动机运行过程的可靠性对于飞行安全起决定性作用［1］。发动机长期工作在高温、高压、高转速等恶劣环境下，气路部件不可避免地会出现叶尖磨损、叶片腐蚀等现象［2-3］，进而导致气路部件性能出现退化，使得超温、失速、喘振等故障时有发生［4］。因此，为提高工作可靠性，有必要开展航空发动机的性能退化评估研究。

航空发动机的性能退化评估主要通过估计发动机健康因子（各部件的效率和流通能力）而实现［3］。目前发动机健康因子估计方法主要分为基于物理模型的方法和基于数据驱动的方法［1］。其中基于数据驱动的方法通过训练大量“测量参数-健康因子”的映射样本，使模型具备由测量参数计算发动机性能衰退趋势的能力，该方法在退化数据集［5］上展现了出色的预测能力［6-8］。但实际上发动机的性能健康因子无法测量，因此基于数据驱动的方法难以应用于实际发动机性能退化评估中。而基于物理模型的方法则不需要发动机的退化先验知识，而是通过发动机性能计算模型和发动机传感器数据的偏差情况对发动机健康因子进行估计［9-11］，本质是一个参数寻优问题。

由于航空发动机是一个复杂的非线性系统，传统的遗传算法在进行发动机健康因子求解时存在精度不高、过早收敛等问题。差分进化（Differential Evolution，DE）算法具有结构简单、控制参数少、计算精度高等优点，在最近20 多年内取得了迅猛的发展［12］。2013 年，Tanabe 和Fukunaga［13］提出了一种基于成功历史的参数自适应差分进化算法SHADE（Success-History based Adaptive DE）算法。之后，又引入了线性种群缩减策略，得到了L-SHADE（Linear-SHADE）算法［14］，该算法在CEC2014 实参单目标优化竞赛中非混合算法获得了最好的结果。L-SHADE 算法在众多复杂问题上都具有很强的竞争力，因此被应用于许多实际工程问题中［15-16］。然而该算法的线性种群缩小策略在初期种群快速缩减中导致种群的多样性受到影响，易陷入局部最优，在面对复杂问题时效果不佳。

基于差分进化算法在参数寻优问题求解中的有效性，同时针对现有L-SHADE 算法的不足，本文提出了一种改进的L-SHADE 算法，通过引入一种非线性种群缩减策略来解决种群快速缩减的问题，通过调整迭代不同阶段的变异能力增强算法的鲁棒性。利用30 个经典基准函数验证改进算法的有效性。在此基础上将改进算法应用于某型发动机性能退化评估中。

1 算法理论

1.1 发动机退化估计

研究对象为某型小涵道比涡扇发动机，主要由风扇、压气机、燃烧室、高压涡轮和低压涡轮等部件组成，各个部件间存在着复杂的耦合关系。研究表明［17］，发动机的性能退化主要表现在旋转部件气路特性（流通能力和效率特性）的变化上。因此，通常定义发动机各旋转部件流量和效率的健康因子分别为

式中：W、η分别为部件的换算流量和效率；下标d、c 分别表示退化发动机和未退化发动机的数据。

考虑部件性能退化后，发动机的非线性性能模型可表示为

式中：u是发动机输入向量，z是发动机测量参数向量，θ为发动机各旋转部件性能健康因子（流通能力SW 和效率特性SE）组成的向量，t为时间变量。

由于部件的健康因子θ无法直接测量或直接由传感器测量参数计算，因此航空发动机气路部件性能退化评估本质是一个不可测参数的估计问题。通常根据测量参数逆向求解式（3）对部件健康因子进行估计：

式（4）的求解需要满足测量参数的数量p不小于发动机健康因子数量n。受安装空间和重量等因素影响，实际发动机传感器数量有限，很难满足测量参数数量不小于发动机健康因子数量这一要求，从而使式（4）求解成为欠定问题，理论上无法求解。

针对上述欠定问题，Stamatis 等［18］提出MOPA（Multiple Operating Points Analysis）方法，假设单个飞行循环过程中各部件健康因子不变，通过选取多个稳态工作点拓展健康因子的求解方程组，以解决方程组求解中存在的测量参数不足的问题。该方法要求所选取的稳态工作点间具有一定的独立性，缓解健康因子求解中存在的多重共线性问题。但是Diakunchak［19］指出，发动机部件的流量和效率的退化程度会随发动机工作状态的改变而变化，这与MOPA 方法各稳态工作点健康因子相等的假设相矛盾，为减小MOPA 方法假设带来的误差，多工作点选取时要求各工作点差异尽可能小。

通过对所研究发动机多架次的实际飞参数据分析，发现该型发动机稳态工作点多集中于一个较小的高压转子转速区间范围（86%～92%）。由于该转速范围较小，因此近似认为在该区域内部件性能健康因子相等。同时在多工作点选取中尽可能选择单个飞行架次中该转速范围内工作差异大的点，以缓解方程组求解中的多重共线性问题，从而获得更好的方程适定性。

因此在单个区域范围内采用MOPA 方法，对式（4）进行拓展后，得

式中：q为MOPA 选择的工作点数量，满足pq≥n。

将式（5）的方程组求解问题转化为优化问题，而转化为优化问题的关键是确定适应度函数。综合考虑测量参数的误差范围、测量参数的关系以及建模误差和测量参数的比值，合理确定测量参数在适应度函数中的权值ωj，则得到的适应度函数为

式中：Ym为实际测量参数值；Ycal为计算参数值；a为工作点编号，a=1，2，…，q；b为参数编号，b=1，2，…，p。通过最小化适应度函数OF 即可估计得到健康因子。

1.2 改进L-SHADE 算法

1.2.1 标准L-SHADE 算法

L-SHADE 算法是基于线性种群规模缩减和成功历史的参数自适应差分进化算法，其对差分进化算法的3 个控制参数（比例因子F、交叉率CR、种群规模N）进行了自适应调整。作为DE算法变体中最有潜力的算法之一，L-SHADE 算法的改进成为了近年来的研究热点［20-21］。

标准L-SHADE 算法的主要步骤分为初始化、变异、交叉、选择，在进化过程中通过参数自适应和线性种群缩减策略对控制参数进行调整。

初始化差分进化算法首先在种群向量的限制范围内随机生成候选解的初始种群，其中第i个种群向量的第j维分量xi，j为

式中：rand［0，1］为0 和1 之间均匀分布的随机数；下标max 和min 为种群限制范围的上下限；i=1，2，…，N；j=1，2，…，d，其中d为种群向量的维度。

变异在差分进化算法中，第G代第i个种群父代向量xi，G会执行变异操作，产生变异向量vi，G。L-SHADE 算法采用Zhang 和Sanderson［22］提出的current-to-pbest/1变异策略：

式中：Fi为缩放因子；xpbest，G是从第G代前pN（p∈[0，1]，乘积四舍五入到整数）个精英个体中随机选择的一个个体；xr1，G∈PG是从第G代N个种群向量集合PG中随机选择的一个个体；xr2，G∈PG∪A，其中A为一个外部存储单元，存储前G-1 代中选择失败的个体，当种规模超过N时，则随机选择一个A中的旧个体替换为新个体。通过引入存储单元A，将劣解纳入变异的过程，增加了种群的多样性。

变异操作可能会使个体数值向量的某个值超出限制范围，通过式（9）对数值进行修正：

交叉实验向量个体vi，j，G由变异向量个体vi，j，G和父向量个体xi，j，G交叉产生：

式中：jrand为［1：d］中的随机整数。通过引入jrand，使每个父向量中至少一维进行交叉操作，从而提高算法的收敛速度。

选择分别计算实验向量和父向量的适应度函数值，遵循适者生存的原则确定下一代个体，将表现更好的向量保留到下一代，数学表达式为

参数自适应控制参数决定了差分进化算法的精度，而人工设置控制参数无法使所设参数满足所有优化问题的需求，因此需要对控制参数进行自适应调整。

在L-SHADE 算法中，采用基于历史信息存档的自适应参数更新策略。在经过选择操作后，每一代选择成功种群的交叉率SCR、缩放因子SF的Lehmer 均值MCR、MF存储在大小为H的历史存储器中。最初MCR、MF初始化为0.5，当进化到新一代时，索引k=k+1，当k＞H时，则令k=1，该策略的历史存储器如表1 所示。

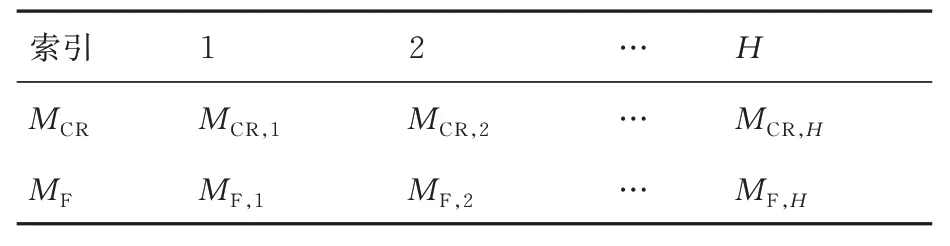
表1 历史存储器Table 1 History memory

在每一代中，每个种群个体xi采用各自的控制参数CRi、Fi，具体由式（12）和式（13）生成：

式中：randn 为正态分布，randc 为柯西分布，ri为［1，H］中生成的随机整数。Lehmer 均值MCR、MF更新方法如下：

式中：Δfk=|f(uk，G)-f(xk，G)|，为成功选择个体和父代个体适应度函数之差；Sk分别代指SCR和SF，为优胜缩放因子和交叉率的集合。通过引入Lehmer 均值，使贡献大的参数具有更大的影响力，较算术均值而言，Lehmer 均值的数值较大，可以避免控制参数过小而造成早熟的现象。

当进化过程中，某一代成功选择个体的数量为0 时，则使CRi的值强制锁定为0，使得每次的交叉过程只更改一个参数，以减缓算法的收敛速度，提高局部搜所能力。

种群规模缩减由于较大的种群规模会使优化算法具备更好的种群多样性，能够拥有更好勘探能力，而较小的种群规模能够增加对有希望区域的利用，使算法具有更好的开发能力，因此种群缩减技术受到了广泛的关注［23］。

在L-SHADE 算法中，通过引入线性种群缩减技术（Linear Population Size Reduction，LPSR）提高算法的效率和收敛性，其中种群缩减遵循

式中：NG+1为下一代的种群规模；round［］为取整函数；Nmin=4 表示进化过程最终的种群大小；Ninit为初始种群大小；Nfes为当前的评估次数；Nfesmax为最大评估次数。

1.2.2 改进L-SHADE 算法

标准L-SHADE 算法在解决无约束优化问题时表现较好，然而在处理复杂的非线性问题时易出现早熟的问题，过分依赖随机生成的初始向量。在解决航空发动机性能退化计算问题时，如果发动机多工作点工作状态偏差较小，进化会出现过早停滞的现象，导致收敛精度不高。由于LSHADE 算法引入了线性种群缩减策略，该方法在迭代初期种群就快速缩减，且在迭代过程中，比例因子过早达到了设定的最大值，这些都增加了过早收敛的可能。针对上述问题，提出了一种改进的L-SHADE 算法。

标准L-SHADE 算法的线性种群规模缩减策略种群变化过程单一，难以满足不同优化问题的需求。文献［24］提出了一种非线性种群缩减策略（NLPSR），其策略如下：

式中：nfesr=Nfes/Nfesmax，为当前评估次数与最大评估次数的比值。

这种种群缩减策略较LPSR 而言减少了总体的评估次数，提高了算法的收敛速度，在针对简单优化问题时是非常有效的。然而与LPSR 技术相同，从第1 代种群就开始减少种群，并没有给个体足够的进化时间，意味着需要浪费部分计算资源来初始化个体并迅速删除它们，造成了种群资源的浪费。且这种方法在进化初期种群规模减小太快，影响了种群的多样性，增加了局部收敛的可能性。

由于航空发动机热力学计算过程极为复杂，其健康因子求解过程并不是简单的单峰值问题，因此需要减缓进化前期种群缩减速度，保持种群的多样性，增强算法全局搜索的能力。同时为提高算法效率，需要在进化后期大幅降低种群规模。针对上述需求，提出了一种新的种群缩减方法，将当前评估次数与最大评估次数的比值nfesr作为指数，1-nfesr为底数，使种群规模在进化初期几乎保持不变，进化后期大幅降低，其表达式为

图1 为不同种群缩减策略种群规模随评估次数变化的对比，其中NLPSR 为文献［24］中的种群缩减策略，改进NLPSR 为提出的种群缩减策略。由图1 可见，NLPSR 和LPSR 在迭代前期种群快速减少，而提出的种群缩减策略在迭代前期种群数量基本保持不变，能够给予初代个体充分的进化时间，增强算法的多样性。

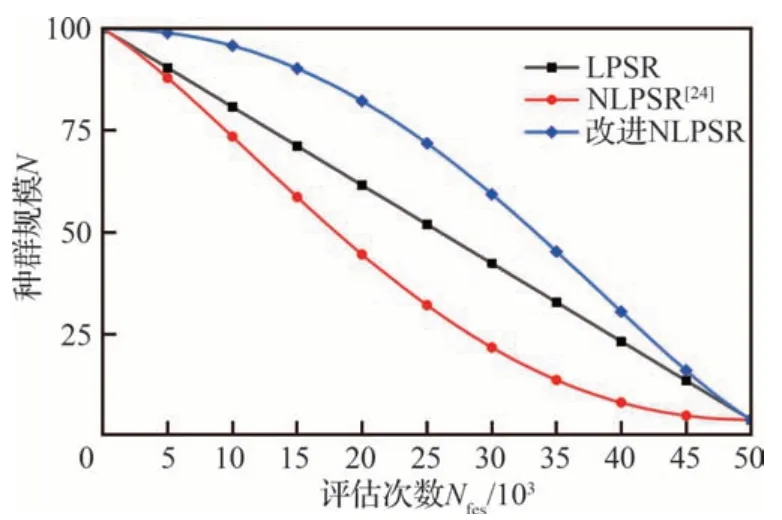
图1 种群规模随评估次数的变化曲线Fig.1 Variation curves of population size with number of assessments

在对种群规模缩减策略进行改进后，发动机性能退化评估求解过程中面临的另一个问题是选择合适的变异策略。

理论上要求所选择的变异策略在迭代初期使用较小的比例因子，以降低贪婪算子在变异过程中的权值，增强算法的全局搜索能力；在迭代后期使用较大的比例因子，以提高算法的局部搜索能力，为此引入Brest 等［25］在jSO 算法中提出的变异策略current-to-pBest-w/1：

式中：Fw为加权比例因子。在发动机性能退化迭代过程中，发现当评估次数大于0.4Nfesmax时，Fw的值会过早达到设定的最大值，导致算法过早收敛，出现早熟的情况。因此提出对Fw的表达式进行平滑处理：

通过对Fw的线性变化，减少了其达到最大值的速度，增强了种群的多样性。这种加权的变异策略与非线性种群缩减技术的目的相同，能够提高算法初期的勘探能力和末期的开发能力。

1.3 改进L-SHADE 算法的流程框架

改进L-SHADE 算法的伪代码如算法1所示。

改进L-SHADE 算法求解发动机健康因子的基本流程如图2 所示。

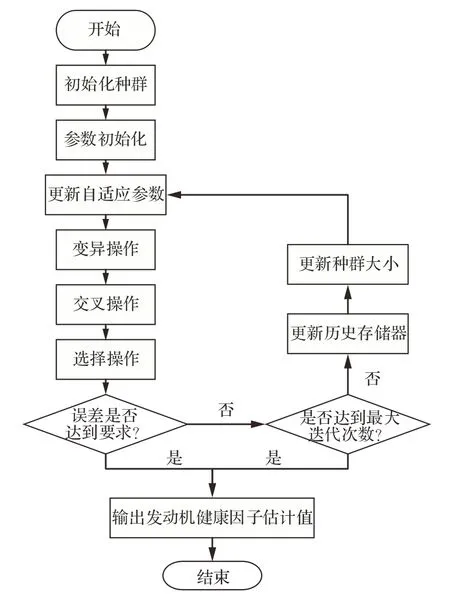
图2 改进L-SHADE 算法流程图Fig.2 Flow chart of improved L-SHADE algorithm

2 改进算法的验证与应用

2.1 改进算法的有效性验证

为证明所提算法的有效性，采用30 个经典的基准函数［26］进行实验，其中30 个函数可分为单峰可分离函数（F1～F5）、单峰不可分离函数（F6～F13）、多峰可分离函数（F14～F18）、多峰不可分离函数（F19～F25）和其他组合函数（F26～F30），具体函数信息可通过文献［26］的网站查寻。将提出的改进L-SHADE 算法与标准LSHADE［14］、L-SHADE-cnEpSin （Ensemble Sinusoidal Differential Covariance Matrix Adaptation with Euclidean Neighborhood with L-SHADE）［27］和L-SHADE-SPACMA（L-SHADE with Semi-Parameter Adaptation Hybrid with CMA-ES）［28］进行对比，其中L-SHADE-cnEpSin 与L-SHADESPACMA 均为CEC2017优化竞赛的优胜算法［29］。

具体的验证细节如下：

1）各算法均采用已有文献中的默认参数设置。

2）各算法的种群大小为100，最大迭代次数为100，每个算法均进行50次独立的重复实验。

3）各算法的优化结果以优化得到解对应的函数值f(x)与函数理论最优解对应的函数值f(x*)差值的绝对值来比较，因此0为优化的最好结果。

4）各算法的性能指标通过50 次实验优化结果|f(x)-f(x*)|的平均值、标准差、最小值、最大值和平均运行时间来体现。

5） 30 个经典基准函数的维度（自变量个数）均设置为30。

6）在Windows7 系统的MATLAB2021a 开展实验，基于Intel®CoreTMi7-9700CPU @ 3.00 GHz 的个人电脑。

表2 为4 种算法在30 个经典基准函数的验证结果，加粗的数据为4 种算法中结果最好的值，空白处表示L-SHADE-cnEpSin 和L-SHADESPACMA 算法没有相应的机制来控制其在指定范围内的搜索，进一步导致优化不收敛的情况。30 个函数中，改进L-SHADE 算法取得最优解的次数为14 次，L-SHADE 算法为3 次，L-SHADE-cnEpSin 算法为4 次，L-SHADESPACMA 算法为9 次。

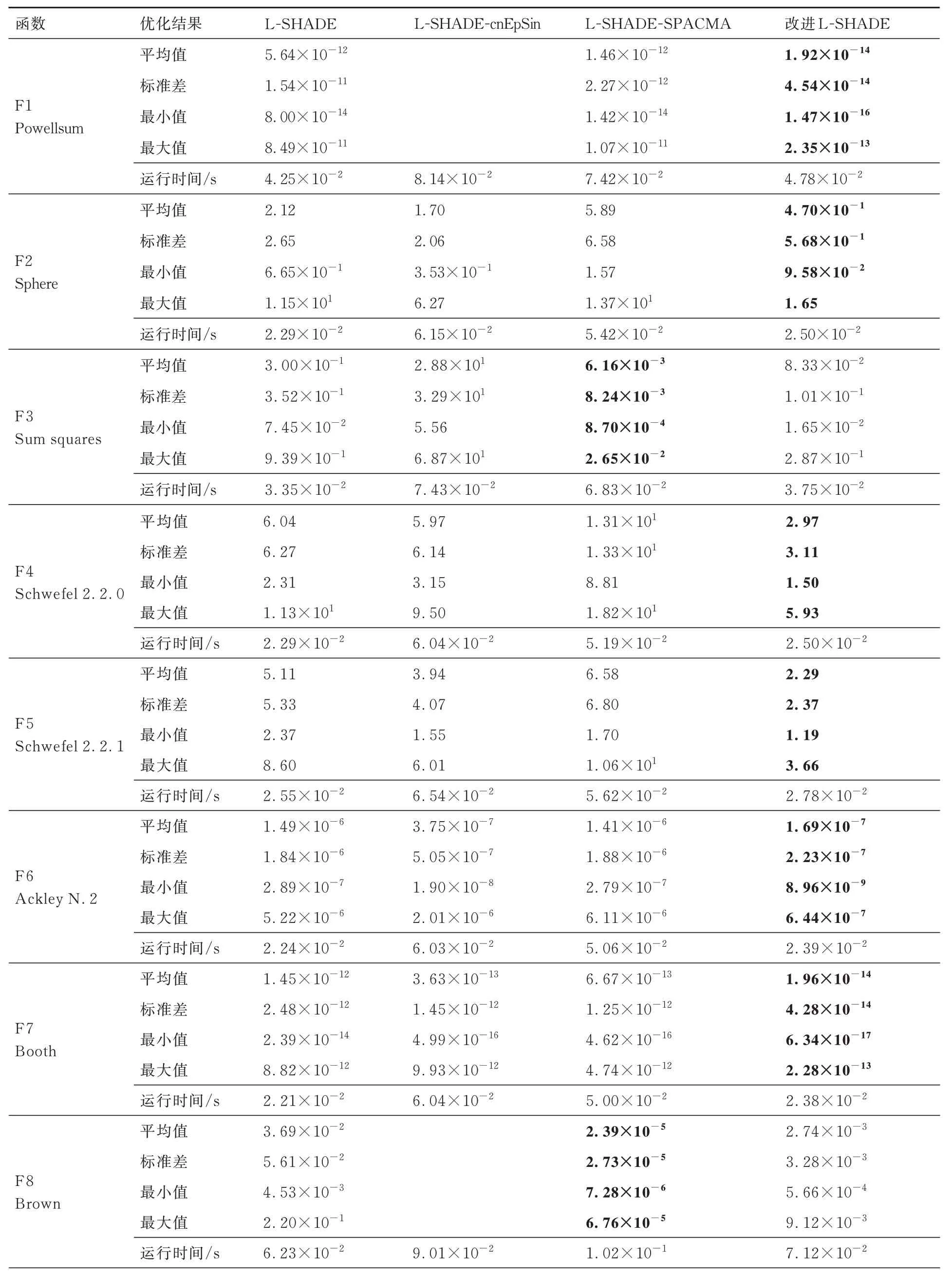
表2 基准函数实验结果Table 2 Experimental results of benchmark functions

其中在单峰函数（F1～F13）中，改进L-SHADE 算法明显优于其他3 种算法。在多峰函数和组合函数（F14～F30）中，改进L-SHADE 算法较标准L-SHADE 算法也具有明显的优势，尽管L-SHADE-cnEpSin 算法和L-SHADE-SPACMA 算法在部分函数中取得了最优解，但L-SHADE-cnEpSin 算法在F18、F20 函数中不收敛、在F16、F23 函数中收敛效果不好；L-SHADE-SPACMA 算法在F24 函数中不收敛。而改进L-SHADE 算法具有更好的鲁棒性，能够适用绝大多数函数。另外，改进L-SHADE 算法的运行时间较标准L-SHADE算法增加不大，但比其他2 种算法运行时间明显减少，降低了算法的复杂度。综上，提出的改进L-SHADE 算法较其他3 种算法具有明显优势。

2.2 改进L-SHADE 算法在发动机性能退化中的应用

研究对象共布置有5 个气路传感器，分别为燃油流量Wf，高压转子转速N2、低压转子转速N1、高压压气机后总压Pt3、低压涡轮后总温Tt5；其中Wf为发动机模型的输入，模型的输出量p为4 个。研究对象的健康因子为该型发动机旋转部件（风扇、低压压气机、高压压气机、高压涡轮、低压涡轮）的效率和流通能力，分别表示为SE12、SW12、SE2、SW2、SE26、SW26、SE41、SW41、SE46、SW46，数量n=10。

为使发动机健康因子估计方程组为非欠定方程，即pq≥n，多工作点数量应满足q≥3。理论上q的值越大，方程组越冗余，健康因子估计效果越好。但在实际情况下，随着q的增加计算成本显著增加，且受发动机传感器测量噪声的影响，数据越多，发动机健康因子的求解越不易收敛，且更容易出现“拖尾”现象，即一个部件的性能退化可能会反映到另一个部件上，使得健康因子向噪声干扰的方向变化。因此q选择为3。

为验证改进L-SHADE 算法估计航空发动机健康因子性能的有效性，以确保输入在发动机的真实飞行包线中，在某型小涵道比涡扇发动机的实际飞参数据中提取高压转子特定转速范围（86%～92%）的稳态数据点，在发动机性能计算程序中预先植入假定的发动机各部件性能退化值，在程序中再输入提取的飞参数据中的发动机的运行条件（飞行高度、马赫数、大气温度）和控制变量（燃油流量Wf），经计算，输出3 型发动机传感器参数（高压转子转速N2、低压转子转速N1、高压压气机后总压Pt3、低压涡轮后总温Tt5）的数值。选用3 组稳态工作点数据代入式（6）中，通过最小化适应度函数求解发动机健康因子。

随机选择2 组预先植入的性能退化量的数据分别为算例1 和算例2，使用L-SHADE、L-SHADE-cnEpSin、L-SHADE-SPACMA 和改进L-SHADE 算法进行健康因子估计，其中各算法的种群大小为100，最大迭代次数为500，健康因子搜索范围为［0.95，1.05］，迭代过程的对比如图3 所示，计算结果如表3 所示。

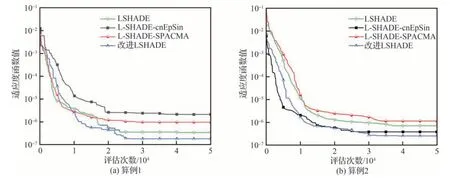
图3 不同算法迭代过程比较Fig.3 Comparison of iterative process of different algorithms

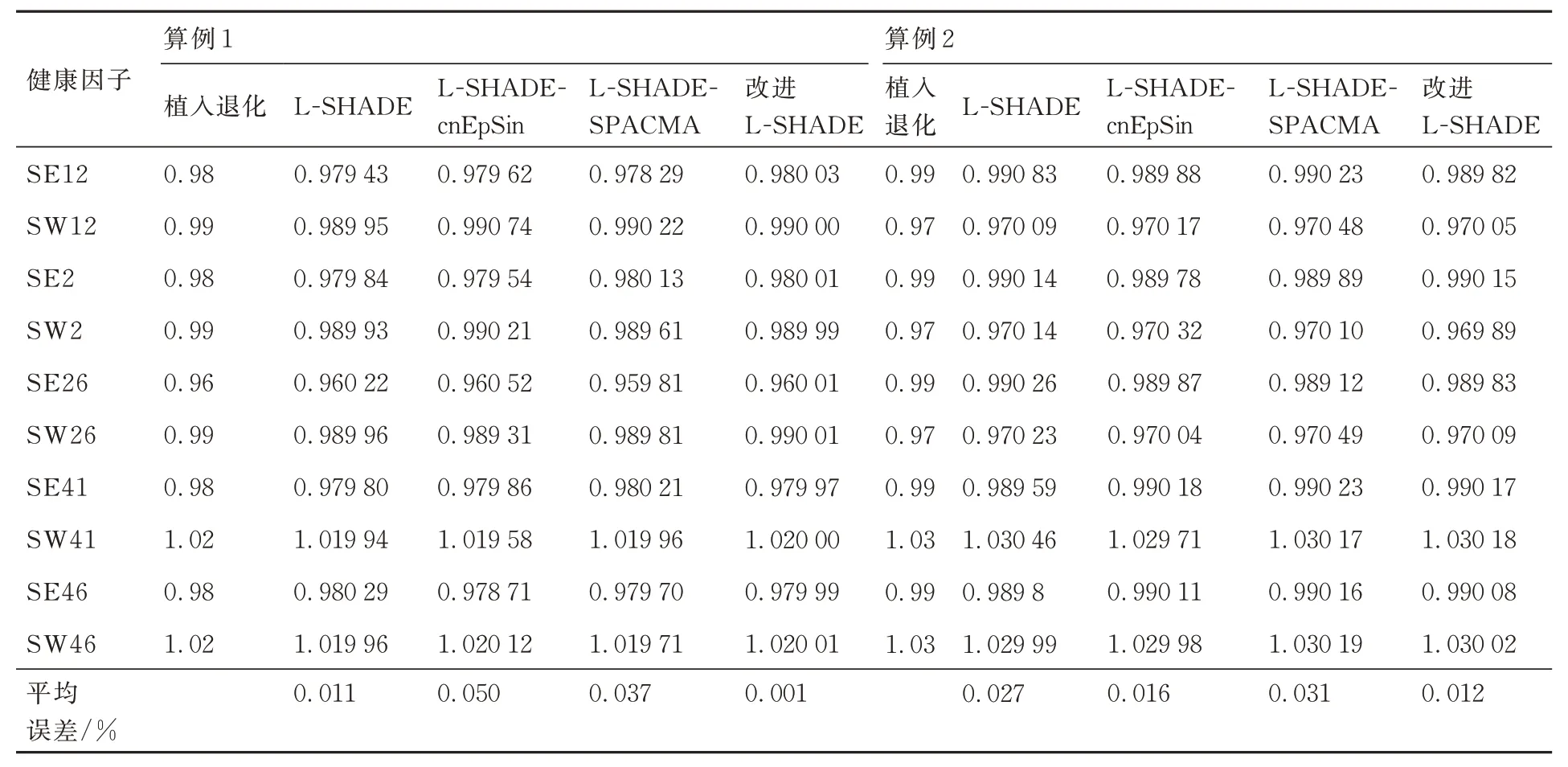
表3 航空发动机性能退化植入和各算法估计结果Table 3 Engine performance degradation implantation and estimation results of each algorithm

由表3 的对比结果可见，改进L-SHADE 算法的计算结果更好，能够满足发动机健康因子估计的工程精度需求。

由图3 的迭代过程比较可见，L-SHADE 算法、L-SHADE-cnEpSin 算法和 L-SHADESPACMA 算法受其种群缩减策略的影响，没有给初代个体充分的进化时间，影响了种群的多样性，在迭代后期易陷入局部最优；而改进LSHADE 算法增强了算法迭代前期的种群多样性和算法后期的开发能力，计算精度较其他3 种算法精度更高。

为进一步验证算法的鲁棒性，对上述2 个算例进行了20 次的重复实验，其计算结果如表4 所示，结果表明所提的改进L-SHADE 算法在航空发动机性能退化评估中具有较强的鲁棒性，计算精度较标准L-SHADE 算法平均提高了65.5%。