埋地管道阴极保护系统的优化分析与研究

2023-08-30丁淑娟胡俊平郭自强

石油工程建设 2023年4期

丁淑娟，左婧，秦虹，胡俊平，郭自强，李盼

1.中国石油华北油田公司第三采油厂，河北河间 062450

2.中国石油华北油田公司第五采油厂，河北辛集 052360

3.中国石油华北油田公司第一采油厂，河北任丘 062552

对于在役油气管道，阴极保护系统与防腐层一起构成了埋地管道的防护体系，使管道免受外腐蚀及杂散电流的影响[1−2]。目前，诸多学者针对阴极保护系统的运行特点和参数优化进行了研究，陈涛涛等[3]针对某燃气门站的阴保系统，结合馈电实验结果，总结了不同阳极地床下的优化方案；赵悦春等[4]通过研究电流开放系统的分布规律和保护效果，得到了适合低压输气管道的阳极地床形式；于淑珍等[5]通过断电实验考察了不同管道共用阴极保护系统之间的影响情况，确定了新建阳极地床的位置；冯朋鑫等[6]通过电连续排查和绝缘性排查测试了联合阴极保护的效果，针对阴极智能系统的升级提出了优化方案。以上研究多通过现场馈电实验及通/断电实验，测试阴极保护的保护效果，阴保系统的优化方案均基于人工经验，导致沿线难以达到较均匀的电位分布，造成现场反复施工，浪费了大量人力和物力。基于此，在电化学实验的基础上，利用极化曲线确定待评价管道的阴极保护电位区间，通过COMSOL 边界元仿真实验确定影响保护电位分布特征的因素，利用模拟退火粒子群算法（SAPSO）对阳极地床的参数进行优化，最后通过实例验证使电位和电流分布达到最佳。

1 实验部分

利用PARATAT 2273 电化学工作站进行实验，试片与待评价管道材质同为X60管道钢，试片尺寸10 mm×10 mm×5 mm，除工作面外均用环氧树脂密封。工作电极为试片，参比电极为饱和甘汞电极，辅助电极为铂电极，腐蚀介质为模拟溶液（按管道沿线土壤成分配置），试片在三电极体系下测试其极化曲线。动电位扫描范围为−1.2～0 V（SCE），扫描速率为1 mV/s。

图1 为X60 钢的极化曲线。从阴极极化曲线上看，试片表面和腐蚀溶液界面之间发生氧化还原反应，电流密度随极化电位的增加而增加。在−1.08～−0.87 mV内，腐蚀电位与电流密度呈线性关系，试片表面的阴极保护效果不断增强；当大于−1.08 mV 时，电流密度突然增加，说明金属表面的负电离子较多，会引发管材发生氢脆反应。因此，将−1.08～−0.87 mV作为阴极保护电位区间，该区间与GB/T 21448—2017《埋地钢质管道阴极保护技术规范》中建议的区间（−1.2～−0.85 mV）相比更加精确，可为下一步系统优化提供数据支撑。

图1 X60钢的极化曲线

2 模拟部分

鉴于有限元法在计算迭代次数、边界条件和网格质量上的局限性，采用模型简化的边界元法进行模拟实验，得到影响阴保电位分布的主要因素。

2.1 控制方程和边界条件

采用“电流分布、边界元”接口求解边缘区域的电解质电势和电流密度，公式如下：

式中：i1为土壤中的电流密度，A/m2；σ为土壤电导率，s/m；φ为土壤中的电解质电势，V。

在阳极地床附近，采用电解质电流密度节点确定外加电流密度。

式中：n为法向向量，指计算域以外；i2为外加电流密度，A/m2。将图1 中阴极极化曲线分段插值后作为埋地管道的边界条件，埋地管道采用固定电位模型，电极电位为0 V。

2.2 模型建立和网格划分

由于该部分只是考察影响电位分布的因素，故采用COMSOL 进行简易模拟[7−8]。模型中管道材质为X65 钢，长1 600 m，规格762 mm × 12 mm，埋深2 m，防腐层电阻率为105Ω·m；辅助阳极为高硅铸铁，长5 m，直径0.1 m，埋深3 m；阳极位于管道中心处，距离管道径向距离为100 m，坐标为（0，−100，−3），土壤为无限空域。网格中最大单元格尺寸为8 m，共形成203个网格顶点、201个边单元和4 个顶点单元，稳态求解精度为0.001。模型和网格划分结果见图2。

图2 模型及网格划分结果/m

2.3 模型求解

考察不同阳极数量对阴极保护电位的影响，结果见图3。2组阳极的坐标分别为（500 m，−100 m，−3 m）和（−500 m，−100 m，−3 m），3组阳极的坐标分别为（400 m，−100 m，−3 m）、（0 m，−100 m，−3 m）、（−400 m，−100 m，−3 m），阳极坐标对称分布。由于采用无限空域作为土壤，因此在土壤边界会出现电位下降的现象，但不影响分析结果。当阳极数量为1 时，靠近阳极地床的管道电位呈漏斗状，电位从管道中心向两端逐渐增加，所有管段处于欠保护状态；当阳极数量为2 或3时，出现了与阳极数量相同的漏斗电位，且整体电位有所下降，阳极数量越多，电位分布越均匀。由于外加电流密度保持不变，因此较多的阳极数量有可能突破析氢电位，造成防腐层阴极剥离。

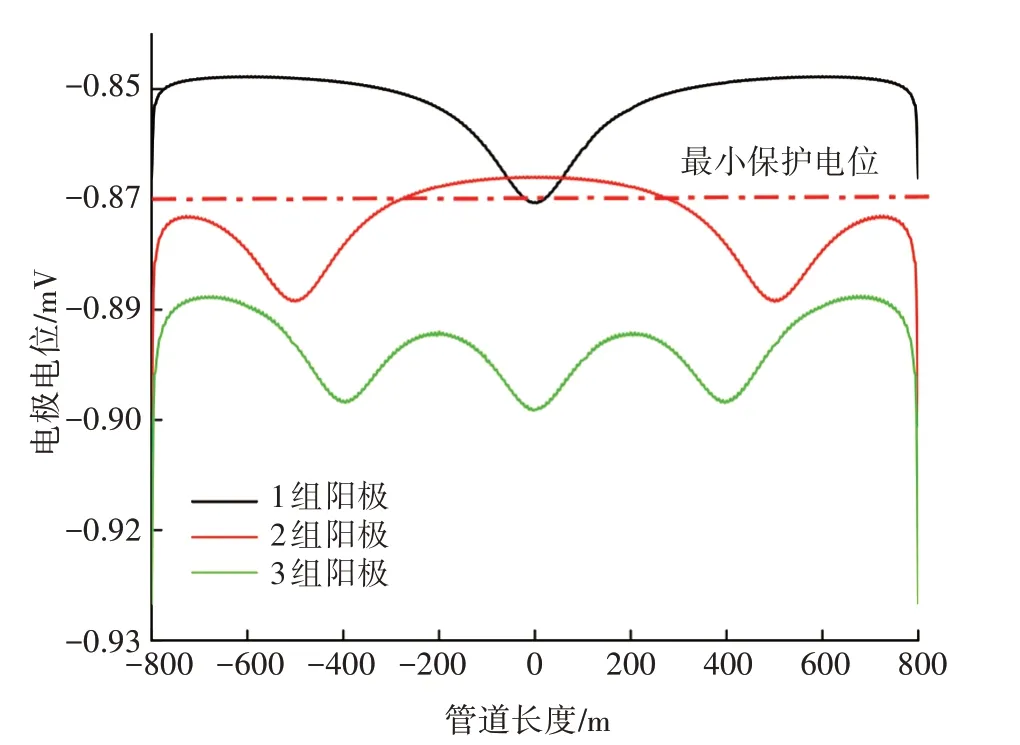
图3 不同阳极数量对阴极保护电位的影响

在3 组阳极的条件下，依次变化阳极坐标中的y和z（代表与管道的径向间距和埋深），考察阳极位置对阴极保护电位的影响，结果见图4。

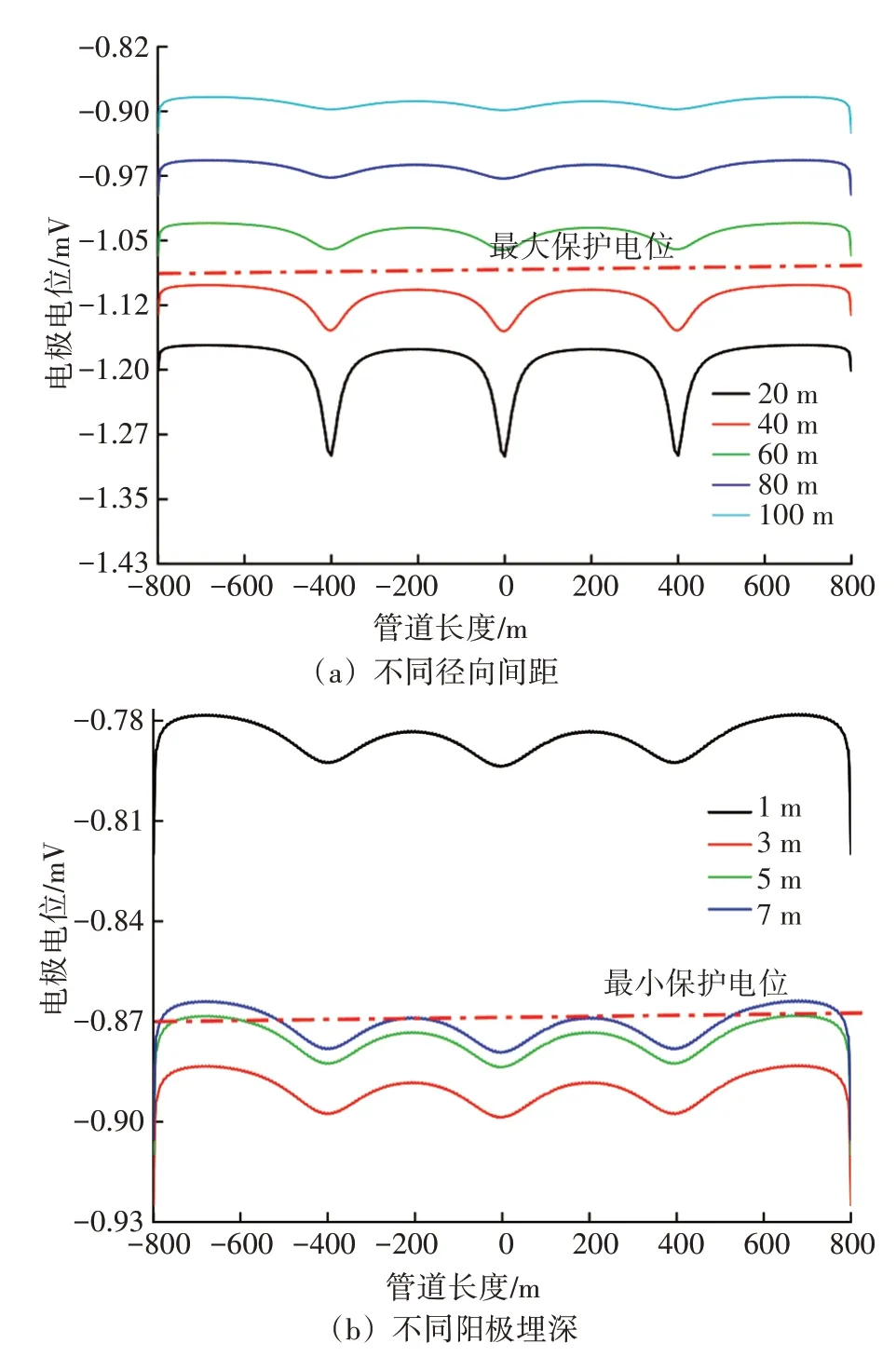
图4 阳极位置对阴极保护电位的影响

当径向间距为20 m 时，阳极地床附近的管道电位迅速负移，且移动速率随间距的减少呈指数增加；在径向间距为20、40 m 时，管道电位已经超过最大保护电位。距离阳极越远，电位分布越均匀，但同时电位也会正移，导致施加在管道上的阴极电流不够，存在欠保护风险。随着阳极埋深的增加，管道电位先负移后正移，在埋深较浅时，管道全线无法达到完全保护的效果，在埋深较深时，部分管段同样存在欠保护现象。因此，对于阳极位置存在最佳的参数选择。

在3 组阳极的条件下，考察恒电位仪输出电流值对阴极保护电位的影响，结果见图5。随着输出电流的增加，保护电位呈不等间距负方向移动，且保护区间变大，电位分布均匀性变差，当输出电流为0.5 A 时，管段全线为欠保护状态；当输出电流为2 A时，保护性最好。

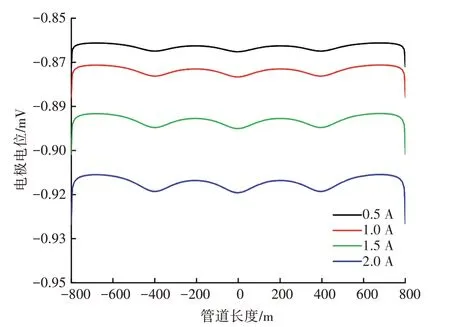
图5 输出电流值对阴极保护电位的影响

在3 组阳极的条件下，考察土壤电阻率对阴极保护电位的影响，结果见图6。

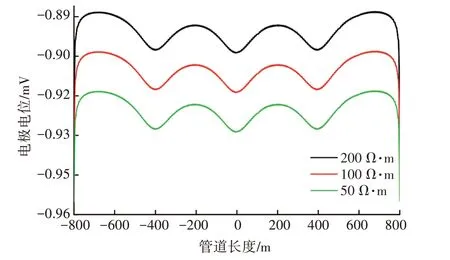
图6 土壤电阻率对阴极保护电位的影响

随着土壤电阻率的上升，保护电位整体等间距正移，电位均匀性不发生改变，电阻率越高，土壤的IR 降越大，能到达管道的保护电流越小，保护效果越差。另外，过大的土壤电阻率会使阴保电位达到析氢电位，产生氢脆风险。

3 基于SAPSO 算法的阴极保护参数优化

通过以上仿真结果可知，阳极数量、阳极位置、输出电流和土壤电阻率等参数决定着管道阴极保护系统的有效性和实用性[9]。考虑到土壤电阻率需根据沿线阳极地床的埋设地点，通过四电极法测量，故不将此参数作为优化变量，只作为固定参数输入。此外，管道外防腐层破损率也与阴极保护的电位分布有关，破损率越大，电位分布越不均匀，保护性越差，破损的地方互成阴阳极，加速腐蚀。

当管道处于保护状态时，管道表面的阴极保护电位应在最佳保护电位附近，且不超过保护电位区间，将管道表面离散成n个点，则管道表面的平均电位的计算公式如下：

式中：φj为j节点的电位值，mV2；φ1（）为管道电位与平均电位之间的差值，反映了电位分布的均匀程度，mV；Ie为输出电流，A；De（x，y，z）为阳极地床的三个位置参数，m；ne为阳极数量，个；φp为最佳保护电位，mV，在此取−0.95 mV；φ2（）为最佳保护电位与平均电位之间的差值，反映了电位优化的效果，mV2。φ1、φ2均为目标函数，两者越小，阴极保护效果越好，反之越差。

将阴极保护参数优化的式（5）、式（6）转化为多目标寻优问题，采用模拟退火（SA）和粒子群算法（PSO）的结合进行求解，算法原理见文献[10−11]。求解过程分3步。

1）初始化粒子的各项参数，包括Ie、De（x，y，z）和ne，设置土壤电阻率和防腐层破损率，以式（5）、式（6）为适应度函数，通过式（7）、式（8）计算粒子的速度和位置信息。

式中：i为粒子序号；d为维度序号；k为当前迭代次数；w、c1、c2分别为惯性权重和加速因子；v、z分别为位置和速度；r1、r2均为0到1的随机数；pi,d和pg,d分别为个体最优位置和全局最优位置。

2）根据Metropolis 法则，当适应度值的增量△E< 0，则新位置的解较优，选择新解；否则，按照概率p=exp（△E/T）选择较优解（式中：T为退火温度）。

3）查找终止迭代条件是否满足0.000 1 的阈值，如果满足则退出当前迭代；否则，以T为控制参数更新粒子的各项参数，重复步骤1）～2）。

此外，式（7）中的w、c1、c2均为定值，无法平衡全局和局部搜索的要求，故采用双正切函数构建随迭代次数变化的动值参数，对SAPSO 算法进行改进，公式如下：

式中：wk、c1，k、c2，k均为对应第k次迭代的数值；K为总的迭代次数；wa、ca为该参数的最大值和最小值之和；ws、cs为该参数的最大值和最小值之差。

4 实例分析

4.1 理论计算

以某输油管道为例，该管道全长143.5 km，管径D355.6 mm，壁厚8 mm，管材为X65，采用石油沥青防腐层，防腐层厚度5 mm。根据防腐层绝缘电阻，通过简易公式计算保护电流密度为30 μA/m2，再利用式（10）计算外加电流阴极保护系统的单侧保护长度L[12]。

式中：△VL为保护电位差值，V；D为管道外径，m；Js为保护电流密度，30 μA/m2；R为单位长度管道纵向电阻，根据管道电阻率、管径和壁厚计算，20.64×10−6Ω/m。

由此得到管道沿线阴极保护站的数量N=L总/2L+1（L总为管道总长度，m），经计算N≈4；阴极保护电流Ie=πDJsL（Ie为外加阴极保护电流，A），经计算Ie=0.83 A。根据SY/T 0036—2016《埋地钢质管道强制电流阴极保护设计规范》和Q/SY 06314.1—2016《油气储运工程防腐绝热设计规范第1 部分：管道防腐层及阴极保护》的相关规定，要求设计的阳极埋深不小于1 m。最终根据经验，设计浅埋阳极的埋深为3 m，距离管道径向距离为70 m。利用管道沿线的阴极保护桩，实测管道保护电位，见图7。

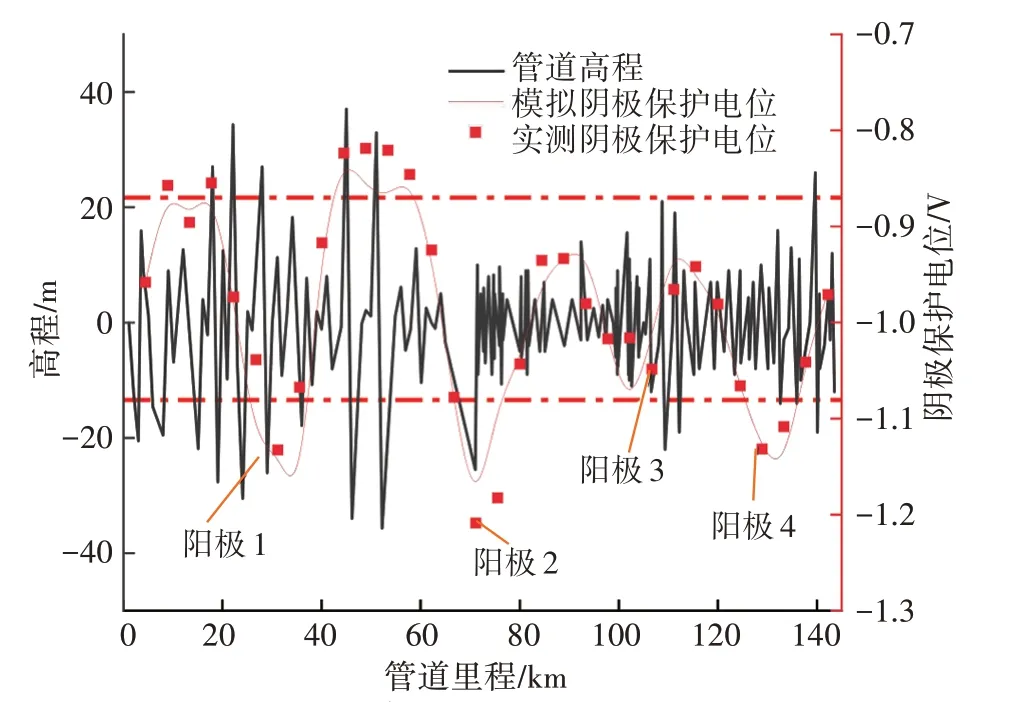
图7 管道沿线阴极保护电位

目前，只有阳极3 所在的管段满足阴极保护电位要求，其余管段在阳极附近的电流过大，而远离阳极的管段又明显保护不足。从该管道的维抢修记录中查阅，发生外腐蚀最严重的管段为40～55 km之间，与实测保护电位相符。此外，通过COMSOL建模，得到实际管道的电位模拟结果，与实测电位差距较小，证明了模拟结果的准确性。

4.2 优化结果

4.2.1 优化方案1

通过SAPSO 算法对阴极保护参数进行优化，Ie、De（x，y，z）、ne的初始值分别采用以上常规设计结果，最终得到5个阳极地床的参数信息，坐标分别为（20.6 km，−68 m，−3.7 m）、（43.8 km，−55 m，−4.1 m）、（71.2 km，−59 m，−4.2 m）、（93.1 km，−31 m，−1.9 m）、（117.7 km，−62 m，−2.1 m），保护电流均为0.95 A。从算法迭代角度看，初次迭代时，优化结果随机分配，较高的退火温度使粒子在迭代过程中表现出随机化和多样化；随着迭代次数的增加，较低的退火温度使粒子逐渐向最优解的位置靠拢，阳极地床的坐标位置逐渐清晰，见图8。

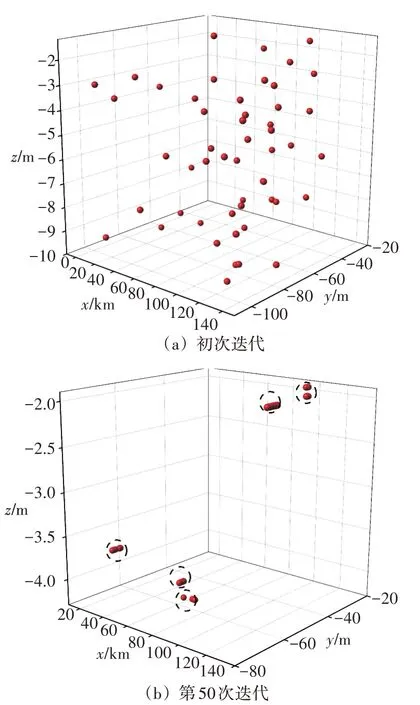
图8 不同迭代次数下的收敛结果

根据优化方案1 定义的阴极保护参数，采用COMSOL 对其进行模拟，见图9。与实际运行方案相比，优化后的阴极保护电位均匀分布在−1.08～−0.87 mV 区间内，且始终围绕在最佳保护电位−0.95 mV 附近，证明了优化算法的可靠性，管道全线的保护效果良好。

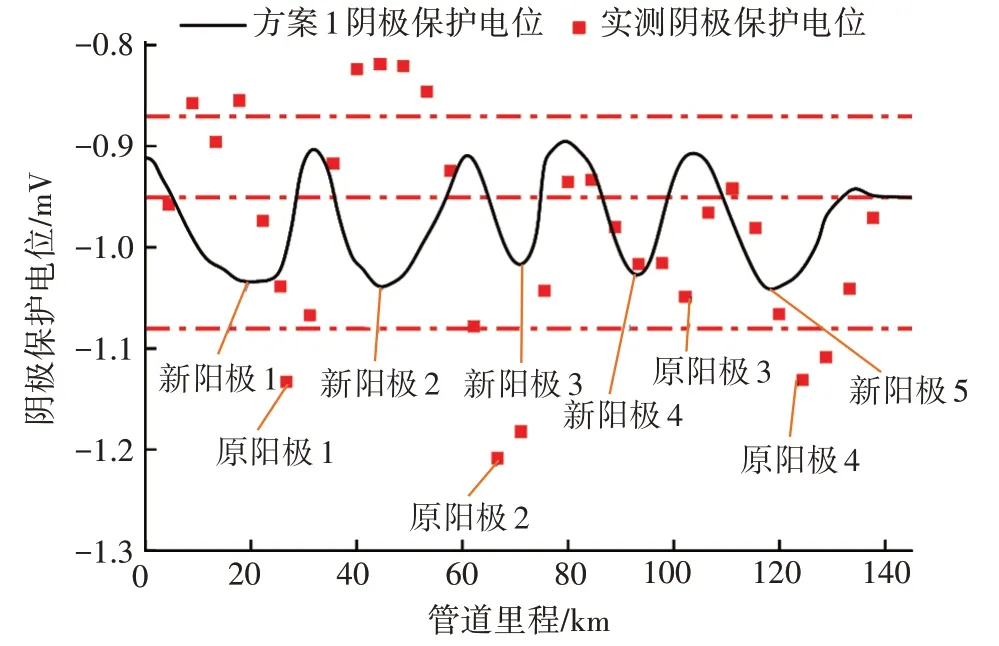
图9 优化方案1的阴极保护电位

4.2.2 优化方案2

将已有4 个阳极地床的位置固定，采用SAPSO算法优化现有阳极恒电位仪的保护电流和新建阳极地床位置。优化后原4 个阳极的I1=0.75 A，I2=0.78 A，I3=0.85 A，I4=0.73 A；新建阳极地床的位置为（53.2 km，−73 m，−3.2 m），保护电流I5=1.05 A，结果见图10。与实际运行方案相比，管道全线保护效果较差，阳极2位置处接近最大保护电位。

4.2.3 优化方案3

将原有阳极1、3、4 的位置固定，采用SAPSO算法优化现有阳极恒电位仪的保护电流，将位置2的阳极地床换为深井阳极，深井阳极由4个贵金属阳极分段构成，每段长6 m，共24 m，阳极直径0.2 m。优化后原有3个阳极的I1=0.71 A，I3=0.84 A，I4=0.72 A；深井阳极的I2=1.73 A，深井阳极的位置为（71.1 km，−59 m，−30.1 m），结果如图11 所示。与实际运行方案相比，管道全线保护效果良好，管道沿线电位分布在最佳保护电位附近，且均匀性较好。

图11 优化方案3的阴极保护电位

4.2.4 方案对比

综上所述，方案1 的优化效果较好，除增加一处阳极地床外，其余阳极地床的位置均有所变化，如对其重新调整埋深，需增加现场施工次数，造成二次开挖；方案2 的优化效果较差，除新增阳极地床外，当阳极2 的恒电位仪出现电流波动时，容易造成析氢风险；方案3 的优化效果最好，深井阳极的位置与原位置相同，只有阳极材料和埋深发生了改变，此时只需对阳极2 进行整改更换即可，不涉及二次征地，对其余已有阴极保护也不构成影响。因此，可选择方案3 作为整改优化方案。