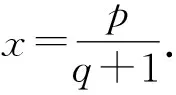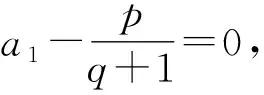一道递推数列通项的多解探究

雷 誉

(湖北省咸宁市青龙山高级中学,湖北 咸宁 437000)

数列是高中数学的重要内容之一,求数列通项公式问题在各种考试中经常出现.在大多数数列问题中,确定数列的通项公式是求解的关键,也是解决数列问题的基础.此类问题的出题方式灵活多变,解法也多种多样.对于既不是等差数列,也不是等比数列,我们需要根据递推关系式的特点,选择合适的方法进行求解.

数学归纳法是高中数学的一种重要方法.通过数列的初始值和递推公式依次计算出数列的前几项,要注意项的表示形式能够反映其规律性,便于发现数列的通项公式,主要考查学生的观察、猜想和归纳的合情推理能力.

迭代法是解决有关数列问题的通用方法,尤其是已知相邻项的递推关系式时十分有效,利用数列的递推关系式依次辗转代入,发现项与序号之间的变化规律,最终转化为第n项和第一项的关系.构造法就是根据题目的条件和结论,构造出一些新的数学形式来解决问题的一种方法.利用累加法求数列的通项公式时,需要将已知的递推关系式进行恰当的变形,整理成下一项与上一项的差和项数之间的函数关系,形如an+1-an=f(n),然后等式两侧对应累加,转化为求f(n-1)+(n-2)+…+f(1)式子的和.

1 题目呈现

题目(2021年八省联考)已知各项都为正数的数列{an}满足an+2=2an+1+3an.

(1)证明:数列{an+an+1}是等比数列;

2 题目解析

2.1 第(1)问解析

分析要证明数列{an+an+1}是等比数列,即证明an+an+1与它的下一项an+1+an+2之比为非零常数,为得到an+1+an+2这一项,需对已知递推式两边同时加上an+1.

证明由an+2=2an+1+3an变形为

an+1+an+2=3(an+1+an).

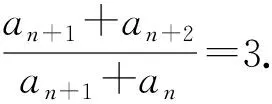
所以{an+an+1}是公比为3的等比数列.

因为a1+a2=2,所以an+an+1=2×3n-1.

2.2 第(2)问解析

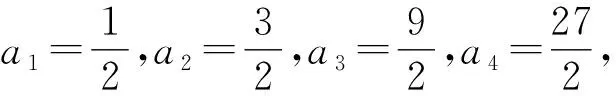
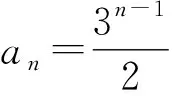
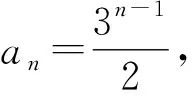
解法3(迭代法)由an+an+1=2×3n-1,得

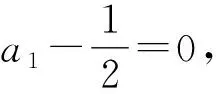
解法4 由an+an+1=2×3n-1,

①

得an-1+an=2×3n-2.

②

①-3×②,得an+1-3an=-(an-3an-1),

an-3an-1=(-1)(an-1-3an-2)=(-1)2·(an-2-3an-3)=…=(-1)n-2(a2-3a1).

又a2-3a1=0,所以an-3an-1=0.

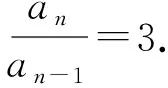
点评解法3配凑系数的技巧性强,从一般项无限迭代下去直到出现含首项的式子,惊奇地发现这个式子结果为零,所以一般项都为零,得到数列{an}的通项公式;解法4由两项的递推式消去含项数的函数部分得到三项的递推式,整理成平衡的结构式,再无限迭代下去直到出现前两项的式子,很巧的是式子结果也为零,所以得到{an}是一个等比数列,通项公式自然也就确定了.

解法5(构造法)设an+2-λan+1=μ(an+1-λan),则an+2=(λ+μ)an+1-λμan.

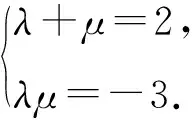
又a1+a2=2,所以{an+an+1}是首项为2,公比为3的等比数列.

故an+an+1=2×3n-1.

③

又a2-3a1=0,所以an+1-3an=0.

④

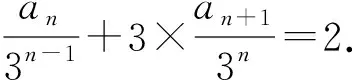
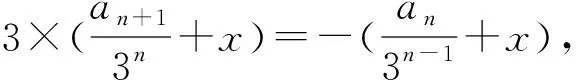
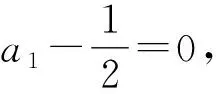
解法7由an+an+1=2×3n-1,可设

an=α·3n-1+β·(-1)n-1,

则an+1=α·3n+β·(-1)n.

所以an+an+1=α·3n-1+α·3n=4α·3n-1.

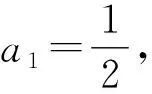
解法8(累加法)将an+an+1=2×3n-1两边同时乘以(-1)n+1,得

(-1)n+1an+(-1)n+1an+1=2×(-3)n-1.

则(-1)n+1an+1-(-1)nan=2×(-3)n-1.

则(-1)2a2-(-1)1a1=2×(-3)0,

(-1)3a3-(-1)2a2=2×(-3)1,…,

(-1)nan-(-1)n-1an-1=2×(-3)n-2.

累加得(-1)nan-(-1)a1=2×[(-3)0+(-3)1+…+(-3)n-2].

解法9由an+an+1=2×3n-1,得

an-1+an=2×3n-2.

作差,得an+1-an-1=4×3n-2.

则a3-a1=4×30,a5-a3=4×32,…,a2n+1-a2n-1=4×32n-2.

累加得a2n+1-a1=4×(30+32+…+32n-2).

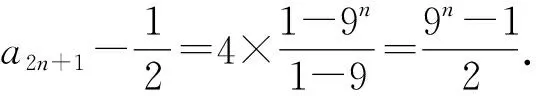
a4-a2=4×31,a6-a4=4×33,…,a2n+2-a2n=4×32n-1,

累加得a2n+2-a2=4×(31+33+…+32n-1).

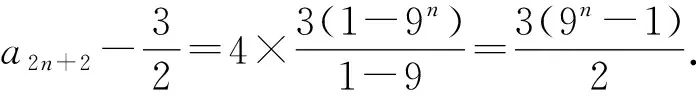
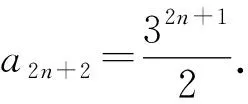
我们知道,若{an}是等比数列,则{an+an+1}也是等比数列,反之是不成立的.下面进行分析和思考:若an+an+1=pqn-1(q≠±1),如何求数列{an}的通项公式呢?