考虑多场景需求的储能和直流系统频率响应特性协同优化方法

丁 可，耿光超，江全元

（1浙江大学工程师学院，浙江 杭州 310005；2浙江大学电气工程学院，浙江 杭州 310027）

随着新型电力系统建设的不断推进，大力发展可再生能源已经成为不可阻挡的趋势[1]。然而，可再生能源具有强波动性和不确定性[2-3]，且随着新能源渗透率不断提高，系统的转动惯量减小[4]，给电网调频带来新的挑战。同时，异步联接后送端电网网架规模减小、负荷频率调节能力减弱[5]，转动惯量进一步降低，导致异步后送端电网的频率波动问题进一步加剧。因此目前送端电网不断提高储能规模，结合直流频率限制控制器(FLC)功能来缓解频率控制问题。

储能具有灵活爬坡特性和双向调节能力，可有效辅助电网频率控制，从而提升高比例新能源电力系统的安全性。文献[6]提出一种基于比例控制的储能调频控制策略，使储能系统模拟常规机组的一次调频响应。文献[7]所提出的控制策略综合了微分控制和比例控制(PD控制)的特点，使储能系统模拟常规机组的惯性响应和一次调频响应。文献[8]提出一种基于模糊逻辑控制的储能快速调频策略，输入系统频率偏差大小及其变化率，然后根据所设计的模糊逻辑策略，输出储能参与快速调频的有功功率。

此外，直流FLC能够根据送端电网频率波动适当地调节输送功率，由于其调节速度快，因此能够给电网快速提供频率支撑功率，防止出现系统频率大幅脱离额定值的情况。文献[9]分析了直流FLC的频率调节效果和动作特性，基于电网常见的扰动设计了直流FLC的参数优化方案。文献[10]通过整定直流FLC的控制环节参数，兼顾直流FLC的调频效果以及功率调节量。文献[11]基于双层优化模型，通过优化直流FLC参数提高不同扰动场景下的送端电网频率特性，且兼顾对受端电网的频率影响。

以上的研究表明，目前电网调频很少考虑储能和直流系统的联合控制，无法统筹地利用各种调频资源。此外，受储能规模和运行成本的限制，单独考虑储能参与调频无法保证系统的频率稳定及调频经济性；而在异步互联的运行方式下，单独考虑直流系统参与调频则难以避免对受端电网频率稳定造成影响。

因此，本工作提出了一种考虑多场景的储能和直流系统频率响应特性协同优化方法。首先，基于某送端电网的仿真数据构建统一频率模型[12]，分析电网在严重故障和常规扰动场景下的调频需求。在此基础上，针对电网在各类场景下的频率问题，构建了储能控制器和直流FLC调频参数的联合优化模型，通过调整两者的调频参数能够兼顾不同场景下的送端电网频率特性、对受端电网的频率影响程度以及调频经济性。然后，根据所建模型的特点采用遗传算法分层递进求解优化问题，实现对储能控制器和直流FLC调频参数的综合最优设计。最后，在MATLAB仿真平台模拟该送端电网的常见扰动进行效果验证。

1 调频需求分析

1.1 频率响应模型

本小节基于某送端电网潮流和机组数据，搭建了电网统一频率模型。统一频率模型是指忽略系统拓扑、潮流，而只考虑机组的调速器-原动机模型和系统的固有频率特性，最终将全系统统一为一个频率。其中，电网的固有频率如图1 所示，其中Meq为系统惯性，由系统全机组惯性特性决定，DL为省内负荷调节系数，另外，新能源包括风电功率和光伏功率，在本模型中主要作为功率扰动之一。

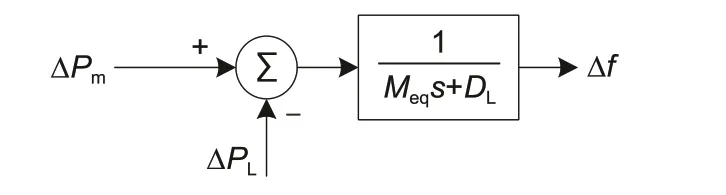
图1 电力系统的固有频率特性Fig.1 Natural frequency characteristics of power system

当系统中有储能和直流接入时，系统固有频率特性可用如下关系式表示：

其中，ΔPG表示常规机组总出力变化，ΔPW表示新能源出力变化，ΔPFLC表示直流的调制功率，ΔPE表示储能出力变化，ΔPL表示系统负荷变化。对式(1)进行差分化，可得电力系统频率的递推表达式：

其中，k1、k2为与系统等效旋转惯量和负荷频率调节效应系数相关的系数，可由如下等式求得：

其中，Δt是差分化的时间步长。

1.2 储能和直流FLC模型

本工作采用基于下垂控制的储能模型[13]，如图2所示。其中，控制器参数主要包括控制系数和调频死区，当系统频率偏差超过储能的调频死区时，根据控制系数动态调整储能的功率指令。储能电站外特性模型参数主要包括功率和SOC 的上下限，确保储能在调频的过程中安全运行。

图2 储能一次调频模型Fig.2 Primary frequency regulation model of energy storage

基于上述储能模型，储能的调频功率指令如式(4)～(6)所示。

其中，PE为储能的有功功率指令；fE,DB为储能电站的调频死区；RE为储能的控制系数；PEmin和PEmax为储能的功率上下限；SOCmax和SOCmin为储能的SOC上下限。

直流FLC 采用目前工程中常用的控制模型[14]，如图3所示。其中直流FLC参数主要包括两个控制系数以及调频死区。

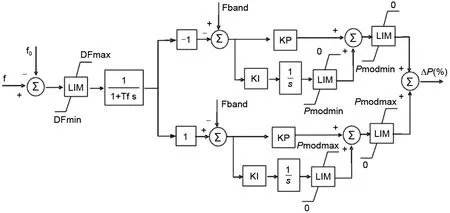
图3 直流FLC控制模型Fig.3 DC FLC control model

基于上述直流FLC 控制模型，直流FLC 的调制功率如式(7)所示。

其中，ΔPFLC为直流FLC的调制功率，KP和KI为直流FLC的控制系数，fFband为直流FLC的调频死区。

1.3 各扰动场景下的频率问题分析

1.3.1 场景选择及分析

根据该送端电网历史故障报告的统计情况，对系统频率造成影响的扰动主要是新能源电站大面积脱网、机组切机以及新能源功率波动三类。其中新能源电站大面积脱网为严重扰动场景，在这类场景下系统的调频需求较高，可通过调整储能和直流FLC的控制系数避免系统触发低频减载；机组切机和新能源波动为常规扰动场景，在这两类场景下系统的调频需求较低，可通过调整储能和直流FLC的调频死区，在满足系统调频需求的基础上，尽可能地减少储能和直流FLC的动作频次，从而减少调频成本。

基于该送端电网常见的扰动场景，通过调整储能和直流FLC的控制系数和调频死区，在都能够满足各扰动场景调频需求的同时，还能提高储能和直流FLC的调频经济性。

1.3.2 调频需求分析

首先模拟严重故障场景，分析电网在该场景下的调频需求，在该故障下电网损失有功功率6000 MW，电网频率偏差情况如图4所示，此时电网频率最大偏差超过了0.7 Hz，电网有触发低频减载[15]的风险，因此需要储能和直流FLC协同改善系统的频率特性。在该场景下，系统频率最大偏差已远远大于储能和直流FLC的调频死区，此时通过调整两者的死区对改善系统频率稳定影响较小，因此需要着重优化两者的控制系数。

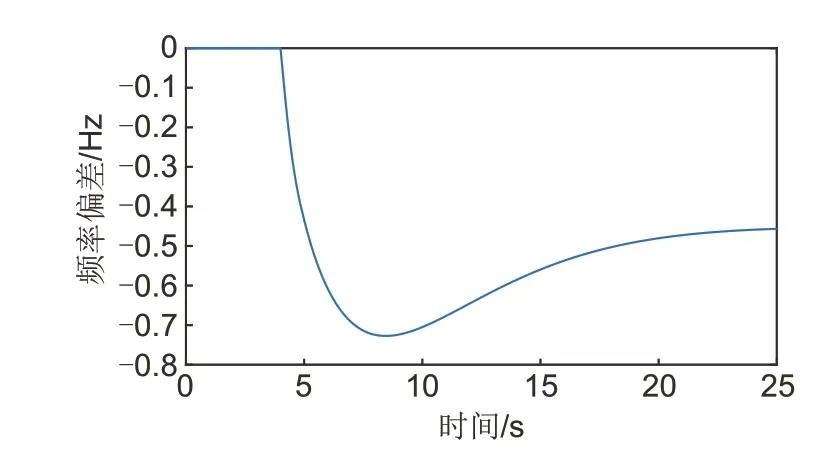
图4 严重故障场景下的频率偏差情况Fig.4 Frequency deviation under large disturbance

其次模拟常规扰动场景，基于某典型运行日的负荷和新能源波动曲线，首先选取新能源波动最剧烈和最缓慢的时段进行模拟仿真，这两类场景下的扰动功率和频率偏差情况如图5、6 所示。其次模拟该典型运行日最大发电功率机组发生故障，此时系统损失696 MW的有功功率，在该场景下的系统频率偏差情况如图7所示。根据仿真结果可知，在这三类场景下，系统频率最大偏差不超过0.1 Hz，此时系统调频需求较小，可以通过调整储能和直流FLC的调频死区在改善系统频率特性的同时减小两者的调频成本，由于目前国内直流FLC的调频死区一般设置在0.1～0.2 Hz(在三类场景下不会动作)，因此在这三类场景下只需要着重优化储能的调频死区。

图5 新能源波动剧烈场景下的频率偏差情况Fig.5 Frequency deviation under the scenario of severe fluctuation of new energy

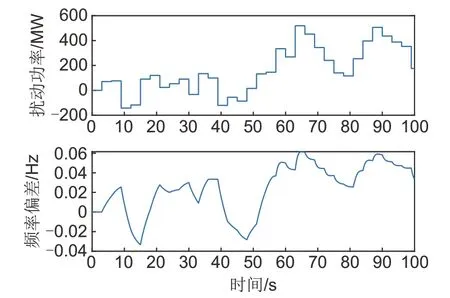
图6 新能源波动轻微场景下的频率偏差情况Fig.6 Frequency deviation under the scenario of slight fluctuation of new energy

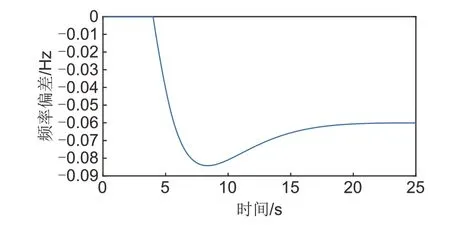
图7 最大发电功率机组故障下的频率偏差情况Fig.7 Frequency deviation under fault of maximum generating power unit

通过上述的仿真分析可知，在严重故障场景下可以通过优化储能控制器和直流FLC的控制系数改善系统的频率特性；在常规扰动场景下，在保证系统频率在安全范围的情况下，可以通过优化储能的调频死区减小储能的使用容量，进而提高调频经济性。

2 储能和直流FLC调频参数联合优化模型

本工作采用双层优化模型调整储能和直流FLC的调频参数。第一层优化针对严重故障场景，通过优化储能和直流FLC的控制系数改善系统的频率特性，避免电网由于频率失稳触发低频减载，同时避免直流FLC 出力过多导致受端电网频率波动过大；第二层优化针对常规扰动场景，在第一层优化结果的基础上进一步优化储能和直流FLC 的调频死区，而根据上述分析，该类场景直流FLC极少动作，因此通过优化储能的调频死区，可以在限制系统频率在安全运行范围的同时提高调频经济性。

2.1 第一层优化模型

2.1.1 目标函数本小节以储能和直流FLC调制功率最小作为优化目标，如式(8)所示，其中储能出力反映调频经济性，直流FLC 出力反映对受端电网的频率影响程度。

其中，λ1和λ2为目标函数的权重因子，ΔPFLC为直流FLC的调制功率，ΔPE为储能的调频功率。

如果λ1较大，意味着优化结果更注重对受端电网的频率影响程度，反之则意味着优化结果更注重调频经济性。目前电网规定在正常运行状态下，系统频率要满足A级标准，即最大频率偏差不能超过0.05 Hz。因此通过对比受端电网在该标准下所能承受的最大扰动功率和直流FLC允许的最大调制功率，即可得到该权重因子的值，如式(9)所示。

其中，ΔPFLC,max为直流FLC 允许的最大调制功率，ΔPre,dis,max为受端电网在频率A级标准下所能承受的最大扰动功率。

2.1.2 约束条件

将送端电网在严重故障场景下的频率约束引入到数学模型中，避免电网触发低频减载，如式(10)所示：

其中，Δfad,max为避免低频减载允许的最大频率偏差，基于所研究电网的实际情况，该值设置为0.5 Hz。

将储能电站SOC 约束和有功功率约束引入到数学模型中，分别写成式(11)和式(12)所示：

其中，SOCmax和SOCmin为储能允许的SOC上下限，PEmax和PEmin为储能允许的功率上下限。

将直流FLC 的调制功率约束引入数学模型中，如式(13)所示：

其中，ΔPFLC,max和ΔPFLC,min为直流FLC 受其过载能力和运行条件所约束的上下限。基于所研究的送端电网的直流参数设计要求，其上下限设为直流额定功率的20%。

2.2 第二层优化模型

2.2.1 目标函数

第二层优化常规扰动场景下的储能调频成本，由于储能使用容量越多，调频成本也越高，因此目标函数设置为储能的使用容量最小，如式(14)所示。

其中，T为仿真区间总时长，Δt为采样间隔。

2.2.2 约束条件

将送端电网在常规扰动场景下的频率约束引入到数学模型中，保证系统频率在安全运行范围内波动，如式(15)所示：

其中，Δfsafe,max为在常规扰动下允许的最大频率偏差，同样根据电网频率安全要求A级标准，该值设置为0.05 Hz。

同时，第一层的优化结果需要引入到第二层模型中，因此储能和直流FLC 的控制系数需要满足式(16)：

此外，同样需要将储能电站SOC 约束和有功功率约束引入到数学模型中，如第一层优化模型式(11)～(12)所示。

2.3 模型求解方法

上述建立的两层优化模型可通过遗传算法进行求解。其中，在第一层优化模型中，通过在1.1 节建立的频率响应模型中模拟严重故障场景，基于模型目标函数和约束条件得到储能和直流FLC最优的控制系数；在此基础上，第二层优化模型中，通过在频率响应模型中模拟常规扰动场景，基于模型目标函数和约束条件得到储能最优的调频死区。本工作采用改进的遗传算法对储能控制器和直流FLC的调频参数进行优化搜索，使求解过程更加高效和准确，其过程如图8所示。

图8 改进的遗传算法流程Fig.8 Improved Genetic Algorithm Process

对于本工作所采用的遗传算法，有以下几点说明：

（1）个体包含四种特征：储能的控制系数和调频死区以及直流FLC的两个控制系数；

（2）个体适应度是两层优化模型目标函数的倒数，倒数越小表明适应度越高；

（3）若在优化模型中无法满足频率约束，则说明通过调整储能和直流FLC的参数无法满足系统的调频需求，需要采取其他措施维持频率稳定。

3 算例分析

3.1 测试系统

本工作基于某送端电网等效网络进行仿真测试，基于1.1 节建立的频率响应模型，从该电网BPA 仿真文件中获取各类机组和负荷的模型和参数，并根据潮流计算的结果，获取电网典型运行日各时段的系统稳态运行点，包括各类机组的有功功率、负荷量、直流系统的有功功率以及新能源的有功功率，从而建立该电网的统一频率模型。由于本工作对直流FLC的调频死区没有进行优化，因此该参数设置为实际运行值0.14 Hz。该电网目前的储能规模为1487 MW/2735 MWh，假设有1000 MW/2000 MWh的储能能够参与调频；该电网目前有两条5000 MW 的直流线路，假设两条线路可以设置同样的优化参数。将该电网典型运行日的新能源波动曲线导入到统一频率模型中，模拟可能发生的各类扰动进行仿真分析。需要注意的是，本工作以一个小时作为一个优化时段，不同时段的参数可根据各个时段的系统状态动态调整，因此选择该运行日的一个时段进行效果验证。

3.2 模型求解

根据该电网的运行状态，首先基于严重故障场景对第一层优化模型进行求解，得到应对严重故障时的储能和直流FLC的控制系数。扰动同样选择为新能源大面积脱网，导致系统损失6000 MW 的有功功率。经过遗传算法迭代求解后，得到储能和直流FLC 的最优控制系数RE,op=1376，KP,op=8.74，KI,op=1.79。

基于第一层优化模型得到的储能和直流FLC最优控制系数，通过模拟常规扰动场景对储能的调频死区进行第二层优化，常规扰动同样选择为新能源快速波动、新能源缓慢波动和机组故障三类场景，分别对三类场景进行迭代求解，最终得到能同时满足第二层模型约束的最优储能调频死区，fE,DB,op=0.013。

目前储能和直流FLC参与调频一般采用固定参数的方法，因此将所提方法优化后的参数与固定参数分别应用于储能控制器和直流FLC 进行效果对比，从而验证所提方法应对不同场景的可靠性，其中固定参数采用电网的实际运行参数。两种方法的具体参数如表1所示。

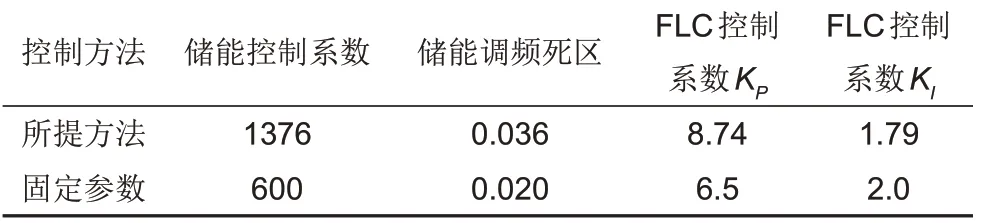
表1 两种方法的参数情况Table 1 Parameters of the two methods

3.3 严重故障场景效果验证

通过第一部分分析，在该场景下系统频率波动严重，有触发低频减载的风险，此时所提方法以优化储能和直流FLC的频率控制能力为主要目标，同时避免直流FLC出力过多导致受端电网频率过度波动。两种方法下的送受端电网频率偏差以及储能和直流FLC出力情况如图9、10所示。

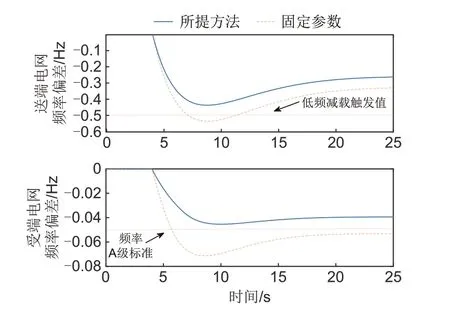
图9 两种方法下的送受端电网频率偏差情况Fig.9 Frequency deviation of power grid at transmitting and receiving ends under two methods

两种方法下的送受端电网最大频率偏差、储能和直流FLC最大出力如表2所示。由表2可知，在该场景下，所提方法下的储能调频功率比固定参数方法较大，直流FLC的调制功率比固定参数方法较小，而储能和直流FLC总的调频功率比固定参数方法较大，这是因为所提方法既要满足送端电网的调频需求，又需要考虑直流FLC出力对受端电网频率造成的影响，因此在所提方法下，送受端电网的最大频率偏差皆小于固定参数方法，即送端电网可以避免触发低频减载，而受端电网频率能够维持在电网频率A级标准范围之内。

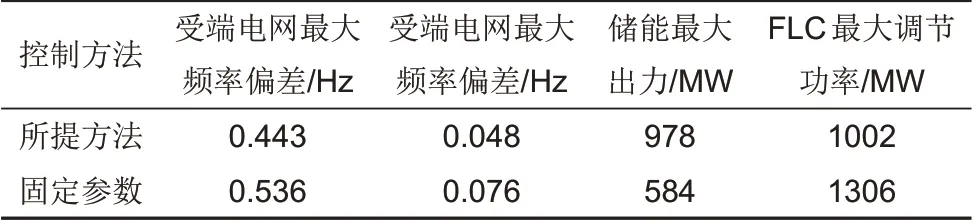
表2 两种方法下的特征量Table 2 Characteristic quantity under two methods

3.4 常规扰动场景效果验证

通过第一部分分析，在该场景下系统频率波动较小，由于在所提方法下，储能为改善其在严重故障场景下的调频性能，设置的控制系数相对较大，因此在常规扰动场景下，所提方法通过优化储能的调频死区，在维持系统频率稳定的同时，减少储能的使用容量，从而提高调频经济性。

首先验证所提方法在新能源波动缓慢场景下的控制效果，系统频率偏差和储能出力情况如图10所示。表3给出了送端电网储能使用容量、储能使用时长和系统最大频率偏差的情况。由表3 可知，由于所提方法适当增大了储能的控制系数和调频死区，因此在频率偏差较大的时刻能够更好地抑制频率波动，同时又减少了储能的动作时长和使用容量，其中，动作时长较固定参数方法减少了42.8%，使用容量较固定参数方法减少了28.6%，兼顾了储能的调频能力和调频经济性。

表3 新能源波动缓慢场景的各类特征量Table 3 Various characteristic quantities of slow fluctuation scenario of new energy

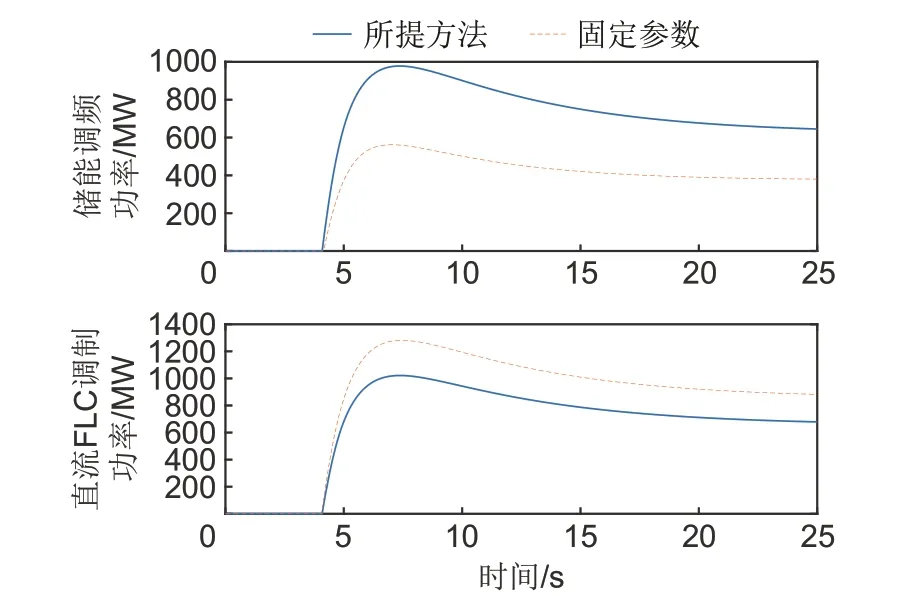
图10 两种方法下的储能和直流FLC出力情况Fig.10 Energy storage and DC FLC output under two methods

其次验证所提方法在新能源波动剧烈场景下的控制效果，系统频率偏差和储能出力情况如图11所示。表4给出了送端电网储能使用容量、储能最大调频功率和系统最大频率偏差的情况。由表4可知，在该场景下，系统频率波动较大，由于所提方法下的储能控制系数远大于固定参数方法，因此相比于固定参数方法，储能在所提方法下具有更好的调频效果，同时使用容量增加了25%，最大调频功率增大了13.9%。可以得出结论，在该场景下，所提方法在付出有限调频成本的基础上，很好地维持了系统频率稳定。

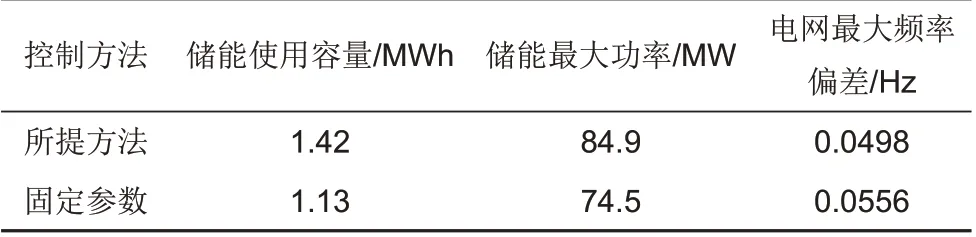
表4 新能源波动剧烈场景的各类特征量Table 4 Various characteristic quantities of severe fluctuation scenario of new energy

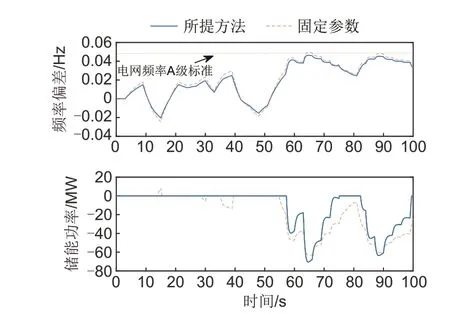
图11 新能源波动缓慢场景的频率偏差和储能出力Fig.11 Frequency deviation and energy storage output in the scenario of slow fluctuation of new energy

最后验证所提方法在最大发电机组故障场景下的控制效果，系统频率偏差和储能出力情况如图12所示。表5给出了送端电网储能最大调频功率、储能启动时间和系统最大频率偏差的情况。由表5可知，由于与固定参数方法相比，所提方法下的储能调频死区较大，因此储能的启动时间较晚，然而由于所提方法下的储能控制系数更大，因此储能在启动后能够更快响应系统调频，并且最大调频功率较固定参数方法提高了27%的基础上，将系统频率波动维持在0.05 Hz，从而确保了系统稳定运行。

表5 最大功率机组故障场景的各类特征量Table 5 Various characteristics of maximum power unit failure scenarios

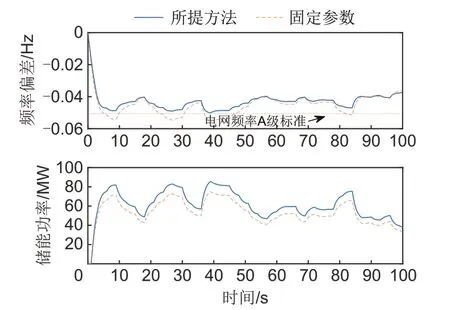
图12 新能源波动剧烈场景的频率偏差和储能出力Fig.12 Frequency deviation and energy storage output in the scenario of severe fluctuation of new energy

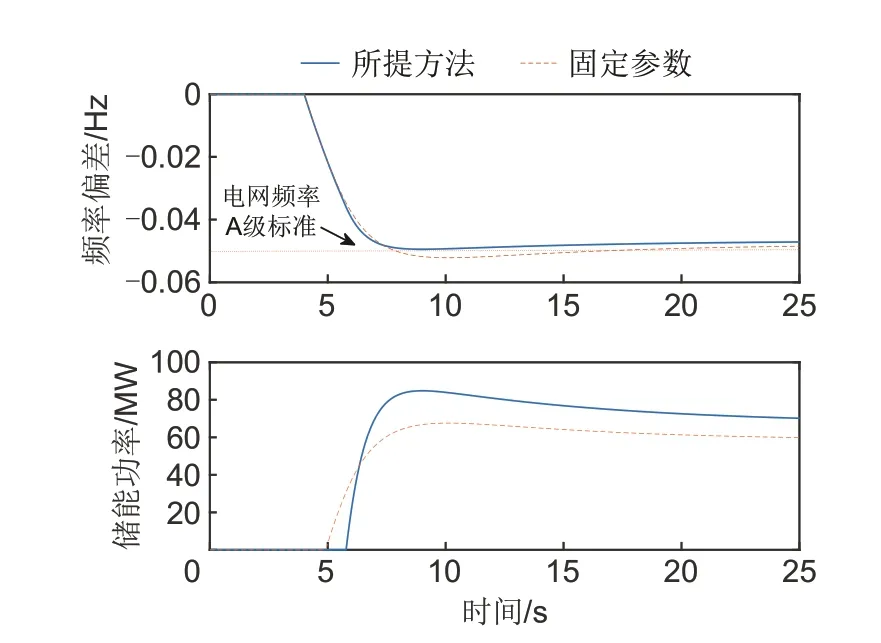
图13 最大功率机组故障场景的频率偏差和储能出力情况Fig.13 Frequency deviation and energy storage output of maximum power unit fault scenario

3.5 工程应用价值

基于上述分析可知，基于电网待优化时段的运行状态，生成可能出现的各类扰动场景，通过对建立的两层优化模型进行求解，能够得到兼顾各类扰动场景调频性能和调频经济性的储能和直流FLC的调频参数，并提前预设储能和直流FLC 的最优参数，能够有效提高系统对各类扰动的预防能力。因此，在实际的工程应用中，所提方法能够在以下两个方面进行优化：

（1）当送端电网在优化时段发生严重故障时，储能和直流系统协同改善送端电网的频率特性，防止其触发低频减载，同时又避免直流系统出力过大导致对受端电网频率造成影响。

（2）当送端电网在优化时段发生常规扰动时，储能在满足系统调频需求的同时，能够尽可能地减少其动作频次，从而提高调频经济性。

4 结论

本工作提出了一种考虑多场景的储能和直流系统频率响应特性协同优化方法，兼顾了各类扰动场景下的送受端电网频率稳定以及调频经济性。主要结论如下：

（1）与固定参数方法相比，基于本工作所提方法对储能控制器和直流FLC 的控制系数进行优化后，能够兼顾在严重故障场景下送受端电网的频率稳定，即在改善送端电网频率特性的同时又防止直流FLC出力过多导致受端电网频率过度波动。

（2）与固定参数方法相比，基于本工作所提方法对储能的调频死区进行优化后，能够兼顾储能在常规扰动场景下的调频性能以及经济性，即在维持送端电网频率稳定的同时尽可能地减少储能的使用容量。