基于ECM的电芯电-热耦合建模与验证

2023-08-29周正柱党会鸿葛志浩

储能科学与技术 2023年8期

狄云，周正柱，党会鸿，葛志浩

（天目湖先进储能技术研究院，江苏溧阳 213300）

电动汽车在复杂工况行驶过程中的高功率充放电会导致电池温升和不均匀性增大，进而导致电池循环寿命下降，引发诸多安全隐患。故对于动力电池产热功率和温度的精确预测需求也日益增长。目前用于研究电池产热情况的测试主要是HPPC 测试[1-2]，但是HPPC 测试亦有其缺点。黄伟等[3]将HPPC测试与Bernardi产热速率模型结合进行电芯温度场仿真，研究表明HPPC测试并不能准确地表示电池持续充放电过程中的极化内阻；通常HPPC电流负荷加载时间短，极化时间短，捕捉极化反应不完整，实际脉冲时间对极化内阻影响较大，HPPC 基本以固定的测试周期和测试倍率来研究，测试精度存在问题[4-5]。如果将HPPC测试替换成恒流充放电搁置测试，进行等效电路模型拟合，其精度如何尚没有清晰的认识。恒流充放电搁置测试，就是研究在恒流充放电撤销后搁置的阶段，在充放电后的静置过程称为弛豫过程[6]，不同于HPPC 测试的是静置时间足够长，让电池在每次脉冲充放电后都能趋于平衡电位，通过延长脉冲与搁置时间，即延长极化演变时间，能完整捕捉到极化演变过程，体现完整的电芯阻值。

本工作以三元锂电为研究对象，通过单体电芯恒流充放电搁置测试辨识相关模型参数，解决HPPC脉冲时间短的问题，减小HPPC测试带来的误差，并建立等效电路模型与Bernardi产热速率模型，在CFD 软件STAR-CCM+中利用ЕCM 模型，针对电池充放电后的弛豫过程的测试数据进行电-热耦合仿真，将仿真与实验数据对比验证，研究电池在不同倍率充放电过程中的产热规律、等效电路模型的适用性以及仿真结果的计算精度，提高对电动汽车在正常行驶工况下的电池性能的精准预测。

1 电-热耦合模型

1.1 等效电路模型

目前研究电池的模型主要有电化学模型[7]、等效电路模型[8]、神经网络模型[9]。二阶RC等效电路凭借其模型参数易于辨识、模型参数精度高、电池测试实验易于执行而被广泛使用[10-12]。故本工作采用二阶RC 等效电路模型模拟单体电芯内部结构，模型结构[13]如图1所示。

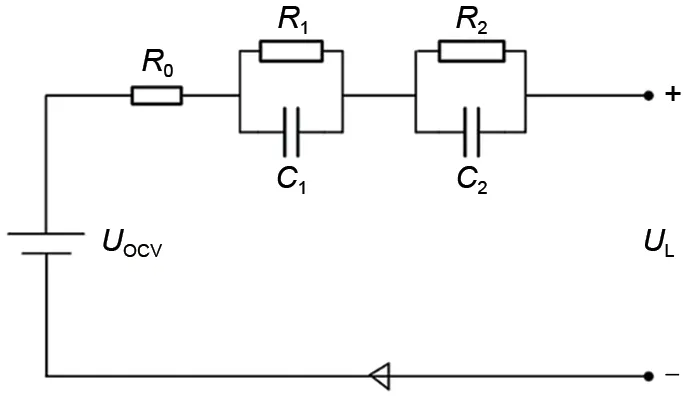
图1 二阶RC等效电路模型Fig.1 Second order RC equivalent circuit model

由基尔霍夫电压定律(KVL)可得，该模型电路的电压可表示为：

锂电池基本数学模型为[14]：

SOC计算方法为：

式中，UL为电源两端电压；Uocv为开路电压；U1、U2分别为两个并联电路中电阻的电压；Ro为欧姆内阻；R1、C1为U1端的极化内阻、电容；R2、C2为U2端的极化内阻、电容；I为等效电路中充放电电流。当电池处于静置状态时，开路电压与电源电压相当，Qref为额定容量，SOC 是根据安时积分法所得[15]。

1.2 热模型

1.2.1 热源计算

总功率是指在一定的电压和电流下纯电阻电路或非纯电阻电路所消耗的电功率，包括不可逆热功率Pir和可逆热功率Pr。总功率计算公式为：

1.2.2 不可逆热计算

不可逆热是不可逆转的产热，主要是由于电芯内阻导致的。通过恒流充放电搁置实验获取RC 参数。通过二阶等效电路模型可以计算电池不可逆热功率，计算公式为：

式中，∆U为内阻两端的电压差，故要输入电阻两端的RC参数计算U1、U2，才能得出电阻两端的压差，模型中规定电流I放电为正，充电为负。

1.2.3 可逆热(熵热)计算

可逆热主要包括反应热[16]。充放电过程锂电池内部会发生一定的电化学反应，这部分反应热通过锂电池外壁面，从电池内部传递到环境中，从而影响环境温度，充电过程中吸热，放电过程中放热；根据Bernardi 产热速率模型[17]，可逆热计算公式为：

式中，dU/dT为熵热系数；U是电池的电压；T为电池的温度。

1.2.4 单体电芯三维热模型

式(8)是三维直角坐标系下，用于计算电芯温度的导热微分方程式，包含内热源、非稳态、变热导率。其中，ρ为单体电芯的密度，c为比热容，λ为各向异性热导率，P总为内热源，由式(5)计算得出，V为电芯的体积，式(9)是牛顿冷却公式，Q为电芯与环境的换热量(热辐射量较小，暂不考虑热辐射影响)，h为表面传热系数，Ts为电芯表面温度，Tr为环境温度，A为电芯表面积。

1.3 电-热耦合模型

电池的温度会影响电池的电性能，电性能也会影响电池的温度，两者相互影响，形成电热耦合模型，如图2所示。电池的发热量是由电和热耦合起来的，发热量的大小影响电池内部电极动力学过程。在STAR-CCM+中，电热耦合模型需要输入初始SOC，结合测试所获得的工况电流，运用安时积分法计算实时充放电过程中的SOC，然后将测试获得的电流I、环境温度Tr输入ЕCM模型，再输入熵热系数，结合Bernardi产热速率模型计算得到Q，将Q输入STAR-CCM+中，计算电池温度T。

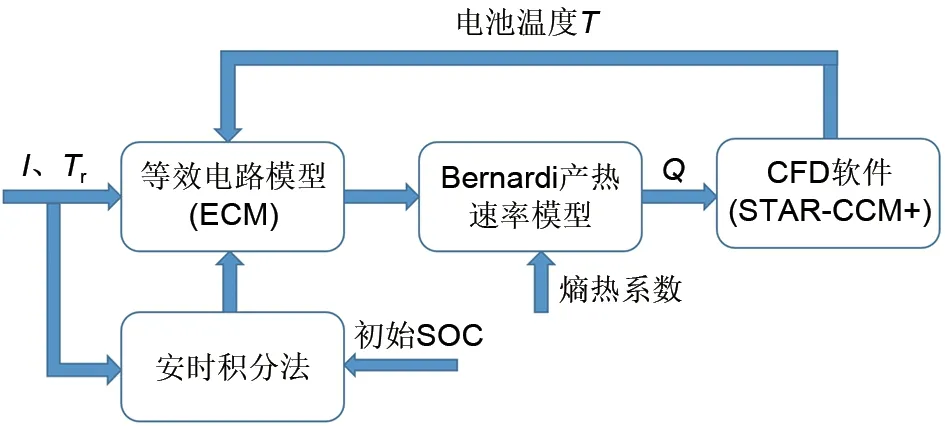
图2 电-热耦合模型Fig.2 Schematic diagram of electro-thermal coupling model

2 实验部分

2.1 实验对象和设备

根据上述理论，RC 参数是模拟锂电池等效电路模型和热模型的关键参数，故针对性开展相关的实验研究。实验以52 Ah可充电镍钴锰酸方形锂电池为研究对象。实验平台主要由高低温烘箱、控制台、充放电设备、夹具设备、温度采集仪(热电偶)组成，如图3 所示。测试系统布置[18]：A 区域，充放电设备及夹具设备区；B区域，实验平台区；C区域，数据采集与输出区。

图3 电芯测试系统实验平台Fig.3 Test platform of battery test system

2.2 测试内容

2.2.1 容量标定实验

通常受电池温度、老化程度影响，电池的实际容量与电池厂家提供的额定容量存在一定的差异[19]。本实验研究在高低温烘箱25 ℃状态下，取三次充放电循环平均值的方法确定电池的可用容量，测试完成后确定所用电池容量为52 Ah。

2.2.2 恒流充放电搁置测试

恒流充放电搁置测试是每次充放电之后要经过较长时间的搁置的实验，搁置有利于电池电压逐渐趋于稳定状态。测试工况分别在10 ℃、25 ℃、55 ℃环境下各以0.33 C、0.5 C、1 C的电流进行充放电实验。例如25 ℃ 0.5 C 恒流充放电搁置测试步骤见表1，电压和电流数据采集间隔为0.1 s。

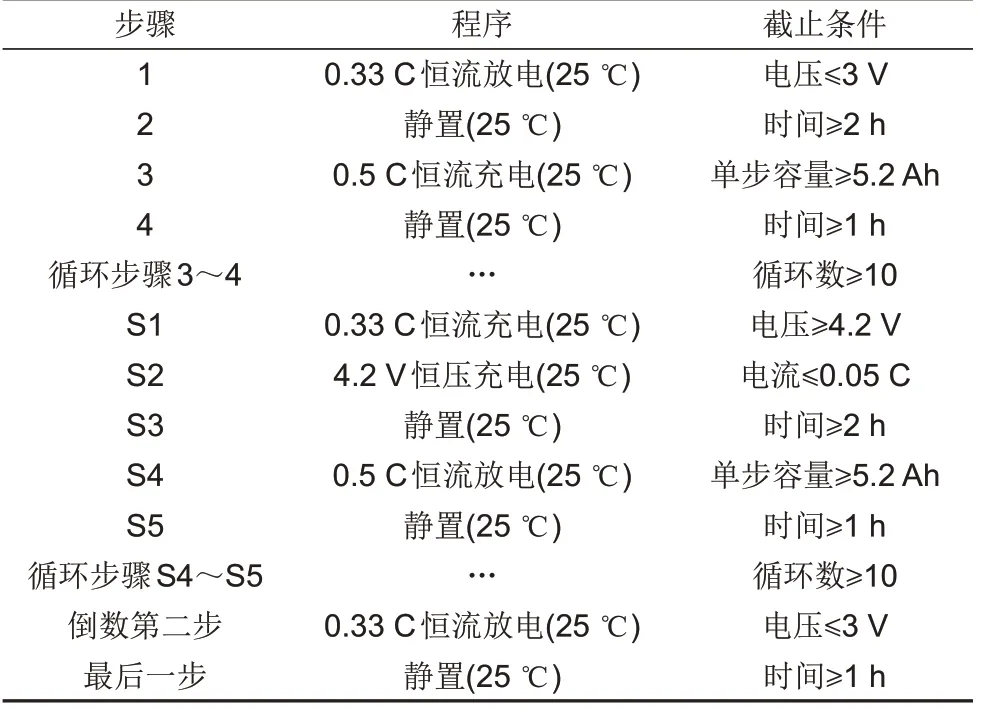
表1 25 ℃ 0.5 C下恒流充放电搁置测试步骤Table 1 Constant-current charge-discharge shelving test Procedures at 25 ℃ and 0.5 C

2.2.3 充放电温升实验

充放电温升实验需要将电池用保温泡棉包裹以营造绝热的环境，然后将电芯置于室温下，设置了6个温度感应监测点，温感通道1、2、3、4、5、6分别布置在电芯表面负极、正极、中心、左下、中下、右下处，监测室内环境温度，分别测试该工况下1 C 放电和0.5 C 放电的温升实验，实验装置如图4所示。

图4 电芯温升测试温探布置Fig.4 Temperature probe arrangement for core temperature rise test

实验过程中每隔1 s 记录整个过程温度、电压和电流，0.5 C放电的温升测试步骤见表2。

表2 0.5 C恒流放电温升测试步骤Table 2 Test procedures for 0.5 C constant current discharge temperature rise

2.2.4 熵热系数dU/dT测试

熵热系数dU/dT为表征锂电池反应热的重要参数，熵热系数的精确测量有助于提高电池产热模型的计算精度。熵热系数测量方法目前主要有两种：直接测量法(又称电位法)和间接测量法[20]。本工作选择相对更容易实现的直接测量法进行测量，电芯无需包裹直接进行充放电，其测试方法见表3。

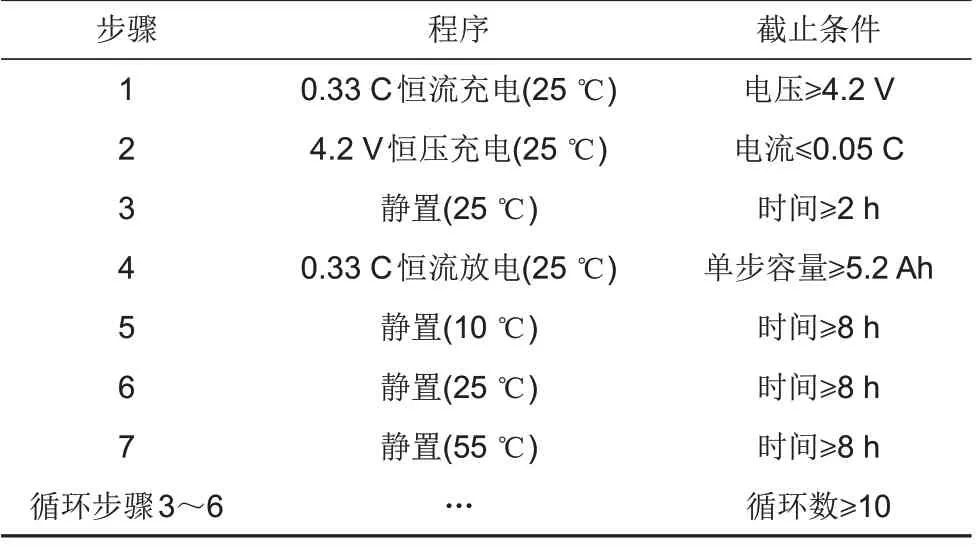
表3 dU/dT熵热系数测试步骤Table 3 dU/dT Entropy heat coefficient test procedures

3 等效电路参数辨识与分析

3.1 参数辨识原理

参数辨识是指在已知模型内部结构情况下，部分参数可能未知，通过输入输出数据来确定模型参数的过程[21]。通过对测试电池进行脉冲充放电，激发电池内部电压响应曲线，将实验数据和二阶等效电路模型结合进行参数辨识。二阶RC 等效电路模型一般有6个参数需要辨识，分别为开路电压Uocv，表征电池趋于稳定时的电压状态；欧姆内阻Ro，表征电池充放电开始与结束端电压的突变状况；极化内阻R1、极化内阻R2、极化电容C1、极化电容C2，表征电池的电化学极化与浓差极化[22]。通过上述恒流充放电搁置测试数据，电池在不同SOC 点经过长时间的搁置趋于稳定状态时采集到开路电压Uocv，还可以获得不同SOC 点处的脉冲充放电弛豫电压曲线，其充放电数据可以辨识其余参数，以25 ℃0.33 C 脉冲放电弛豫电压曲线50% SOC 处为例，如图5所示。

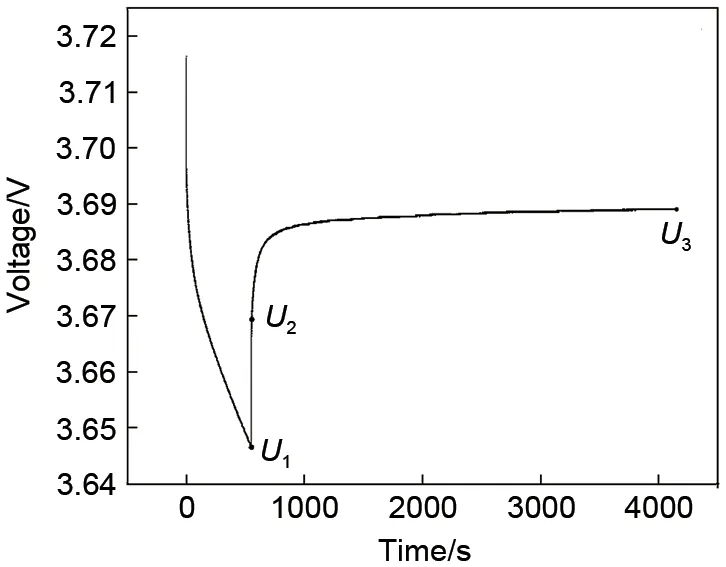
图5 50% SOC处25 ℃ 0.33 C脉冲放电弛豫电压曲线Fig.5 Pulse discharge relaxation voltage curve of 0.33 C at 25 ℃ at 50% SOC

由图5可知，U1是放电结束时刻电压，U2是在电流撤销后电压瞬间跳变后的值，由U1至U2可得，电池在放电结束时刻，撤销电流时，电压会产生突然的回弹，这是欧姆极化造成的电压回弹现象，弛豫阶段RC回路的R0，计算公式如下：

由图5 可知，U3为电池静置结束时刻的电压，由U2至U3可得，电池在弛豫过程，电压会具有一定的“回弹特性”，这是因为电化学极化和浓差极化的共同作用而产生。通过弛豫电压曲线可以辨识出极化内阻R1、R2和电容C1、C2，计算公式如下：

3.2 参数辨识结果分析

通过式(10)～(13)，利用最小二乘法辨识出RC参数。最小二乘法是数据拟合优化的方法，通过最小化误差的平方和寻找数据的最佳函数匹配，最小二乘法公式如下[23]：

式中，yi为多组观测样本数据；y为拟合模型函数；E为残差平方和，根据最小二乘法原理，残差平方和需要达到最小化，同样，可以拓展到多元线性回归模型，样本简化后的最小二乘估计为[24]：

根据式(14)、式(15)利用最小二乘法，将测试数据利用式(11)进行拟合。例如25 ℃ 0.5 C工况下电芯在15% SOC下的脉冲放电电压数据拟合情况，如图6所示。

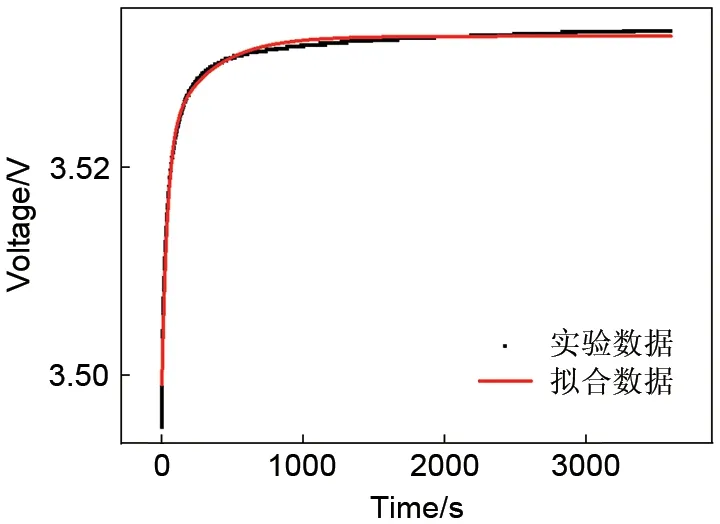
图6 15% SOC处25 ℃ 0.5 C脉冲放电弛豫电压拟合曲线Fig.6 Fitting curve of pulse discharge relaxation voltage of 0.5 C at 25 ℃ at 15% SOC

在10～55 ℃的环境温度下，设置0.33 C、0.5 C、1 C恒流放电工况，其中图7青色代表低温10 ℃，蓝色代表25 ℃，红色代表55 ℃。由图7(a)可知，在30%～70% SOC 区间，呈现的规律为温度越高，OCV越大；SOC两端的OCV变化趋势较快，SOC 在20%～80%区间的变化相对平缓。0% SOC 处的极化较严重，故OCV 变化较大，低温极化现象亦较大，致电芯放电容量偏小，电池的续航里程缩短。

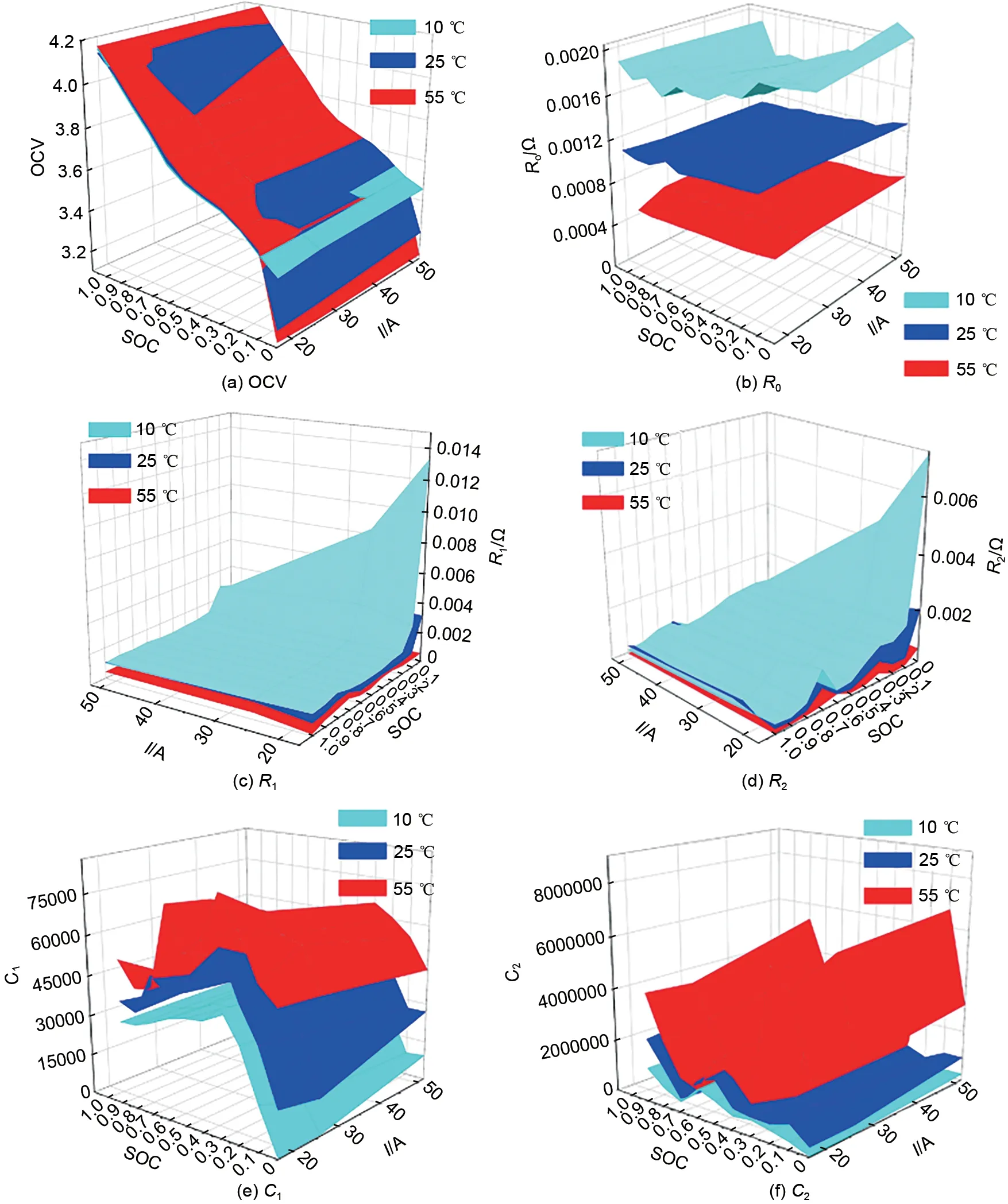
图7 RC参数辨识结果Fig.7 Identification results of RC parameters

在相同工况下，由图7(b)可知，欧姆内阻随温度的升高而减小；在常温25 ℃和低温10 ℃环境下，欧姆内阻变化率相对较大，在高温55 ℃环境下，SOC 和电流的变化对欧姆内阻影响较小。由图7(c)、(d)可知，极化内阻随温度增高而减小；低温低SOC 下正极脱锂困难，极化增大；不同温度下，欧姆内阻随温度的变化率高于极化内阻的变化率。

在10～55 ℃的环境温度下，分别以0.33 C、0.5 C、1 C 恒流充电和放电状态差异不大。充电时，OCV 在SOC 充电到30%～70%时，温度越低，OCV 越大，SOC 两端会存在交叉变化；在充电时，内阻变化率相对没有放电时大，放电时内阻变化更大。由图7(e)、(f)可知，电池电容随温度增高而增大，放电时电容在50% SOC 时会有一定的突变情况发生，呈现非线性的特点。

4 仿真与实验数据对比验证

4.1 网格划分及其边界条件设置

4.1.1 网格划分

根据电池结构将其简化为一个电芯和两个极柱的几何图形，在10～55 ℃范围内，将实验所得的数据导入STAR-CCM+进行三维模型的绘制、网格划分、数值模拟仿真等。三维模型及网格划分，如图8所示。

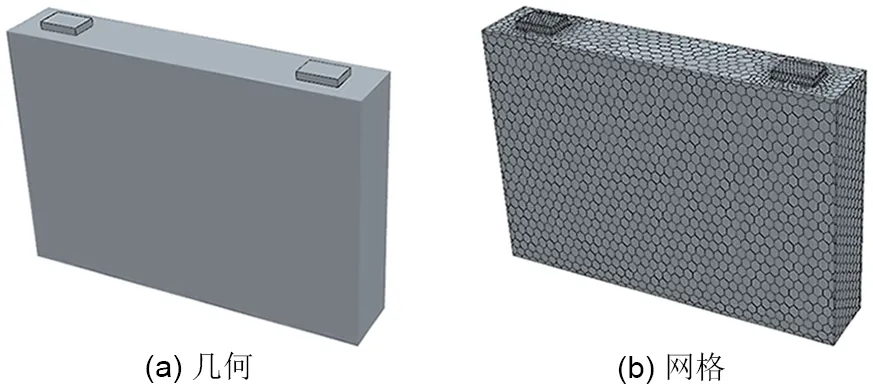
图8 电芯三维模型及网格划分Fig.8 3D model and mesh of battery

4.1.2 边界条件及电池模型

根据实际的电芯规格书所示物理参数与实际测量所得物理参数可知，比热容设置为1060 J/(kg·K)，电芯热导率设置各向异性，与厚度方向平行的电芯热导率为1 W/(m·K)，其余方向为20 W/(m·K)，密度设置为2218 kg/m3。设置对流换热，由于对流换热工况不一致，对流换热系数也不一致，根据牛顿冷却定律确定换热系数[25]，对于无包裹的换热系数设置为30 W/(m2·K)(烘箱内部有风扇吹风散热)[26]；对于有泡棉包裹的电池换热系数设置为2.5 W/(m2·K)；在NЕDC 工况下，由于在常温没开烘箱的环境下，电池换热系数设置为5 W/(m2·K)。

在设置好上述电芯物理参数后，在STAR-CCM+中BSM 模块根据不同电压、电流和温度的电芯，结合等效电路模型进行插值。模拟在负载循环电路中电池电压响应和温度变化的过程，在温度和倍率范围内其他自定义工况下，电池的电压和温度依然能够精确模拟。

4.2 电压精度验证

电压精度验证就是对于不可逆热部分的验证。建立模型，输入拟合之后的RC参数，在STAR-CCM+中进行拟合，输入实验工况的电流值，得到等效电路模型反馈的电压响应。在低温(10 ℃)、常温(25 ℃)、高温(55 ℃)工况下，电池分别在0.33 C、0.5 C、1 C电流工况下的恒流充放电搁置测试，共9 组实验，18 组充电和放电数据，验证了10～55 ℃下所得电压响应模拟值、实际测试值、误差值，由于实际数据量太大，故选其中部分大倍率充放电下的仿真模拟情况展示，如图9所示。

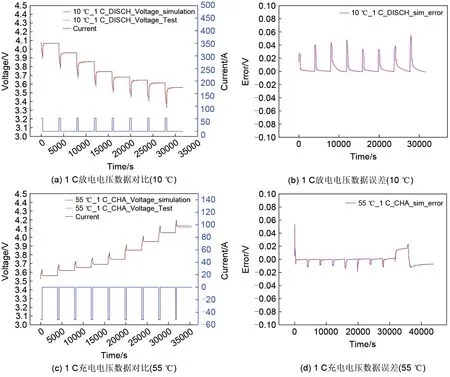
图9 不同温度不同倍率下仿真模拟与实验数据对比及其误差情况Fig.9 Comparison and error of simulation and experimental data at different temperatures and different current

由仿真验证可知：在0% SOC 与100% SOC处电芯的极化反应剧烈，带来的电压响应误差也较大，在10 ℃温度较低时，锂电池在放电过程中锂离子因受到阻力活性减小，在正极的嵌锂量减少，极化增大导致误差增大，但是从图9(a)、(b)中可以看出在90% SOC至20% SOC下，电芯1 C放电电压误差在60 mV以内，说明等效电路模型在低温大倍率1 C 充放电下能较精确预测电压。在低SOC和高SOC处需要加密SOC测试取点间隔，从而减小因极化反应带来的误差。

从图9(c)～(f)可知，在55 ℃ 1 C 大倍率恒流充放电工况下，在10%～100% SOC 范围内，高SOC处与低SOC处的电压误差在60 mV以内，在20%～90% SOC处，电压响应误差在25 mV以内，因此等效电路模型在高温大倍率充放电工况下能够较为精确预测电压。

在常温25 ℃工况下，是动力电池使用的常规工况且使用频率最高，因此在常温下加密SOC 取点进行测试，根据图9(g)、(h)可知，在25 ℃下加密SOC 测试取点间隔后明显由于极化反应产生的误差减小，在10%～95% SOC 处误差在25 mV 以内，在5% SOC处误差也仅有46 mV。

综上，在10～55 ℃环境温度下，电芯在0.33～1 C 倍率工况下，电芯在中间段SOC 处的精度较高，而在高SOC与低SOC处，还需要在进行测试过程中加密SOC取点间隔减小误差。

4.3 温度精度验证

根据上述表3 进行的电芯dU/dT测试，得到该NCM 电芯的熵热系数，将实验数据通过样条插值方法加密SOC 取点，原始实验数据与插值后的熵热系数如图10 所示，其中电压测量仪器的精度等级达到5%，电压能精确到0.1 mV。将熵热系数通过STAR-CCM+中的BSM 模块进行计算得到电池在不同倍率下放电温升情况。

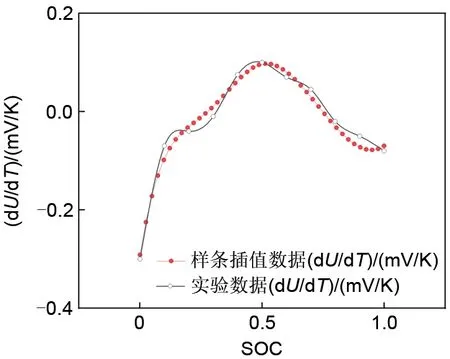
图10 52 Ah的NCM电芯熵热系数Fig.10 Entropy heat coefficient of 52 Ah NCM battery

设置电芯在室温工况下分别在0.5 C和1 C放电情况下的温升，验证Bernardi产热模型中可逆热部分的预测精度。由于是将电芯运用保温泡棉包裹后置于室内，室温会有轻微浮动，在模拟时根据其实际测量到的环境温度为初始温度，选择电芯表面布控的6 个点的温度与模拟仿真温度进行误差比较。仿真与实验模拟的电压、温度数据及其平均误差、温度云图，如图11所示。

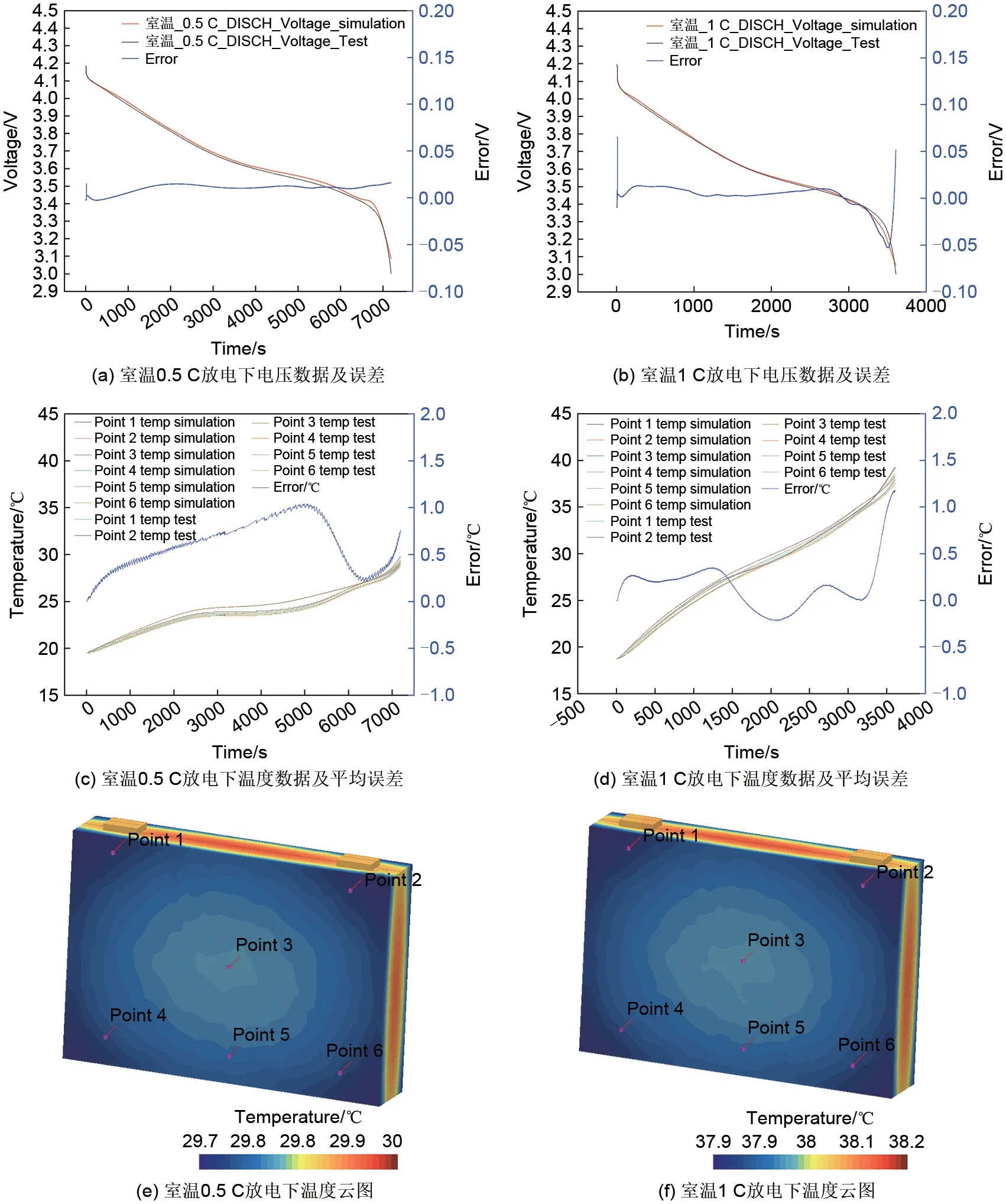
图11 室温不同倍率放电下电-热耦合模拟与实验数据对比、误差及其温度云图情况Fig.11 Comparison of simulation and experimental data of electrical thermal coupling under different rate discharge at room temperature, and its error and temperature cloud map situation

由图11可知：室温下电压误差控制在了55 mV以内，在0% SOC 附近误差较大，其余SOC 处精度更高。0.5 C放电时温升达到10 ℃左右，最大误差温度在1 ℃，1 C放电时温升达到18 ℃，最大误差在1.16 ℃。总体而言，上述研究结果表明等效电路-热耦合模型对于常规的NCM 电芯，在10～55 ℃温度范围内，及0.33～1 C放电倍率下精度较高，具有一定的适用性。

充放电温升测试实验与仿真误差主要来源于：

（1）几何建模与实际电芯有一定差距，同时仿真为均匀热源，实际电芯里面电流密度是不均匀分布的；

（2）散热条件与实际情况也不一致，仿真没有包裹材料，实际外部包裹一定厚度的泡棉；

（3）RC参数辨识存在一定误差。

4.4 NEDC工况下精度验证

在STAR-CCM+中将上述工况下辨识的RC参数输入软件，验证在常温环境下，NЕDC工况下等效电路-热模型的预测精度。模拟结果如图12所示。

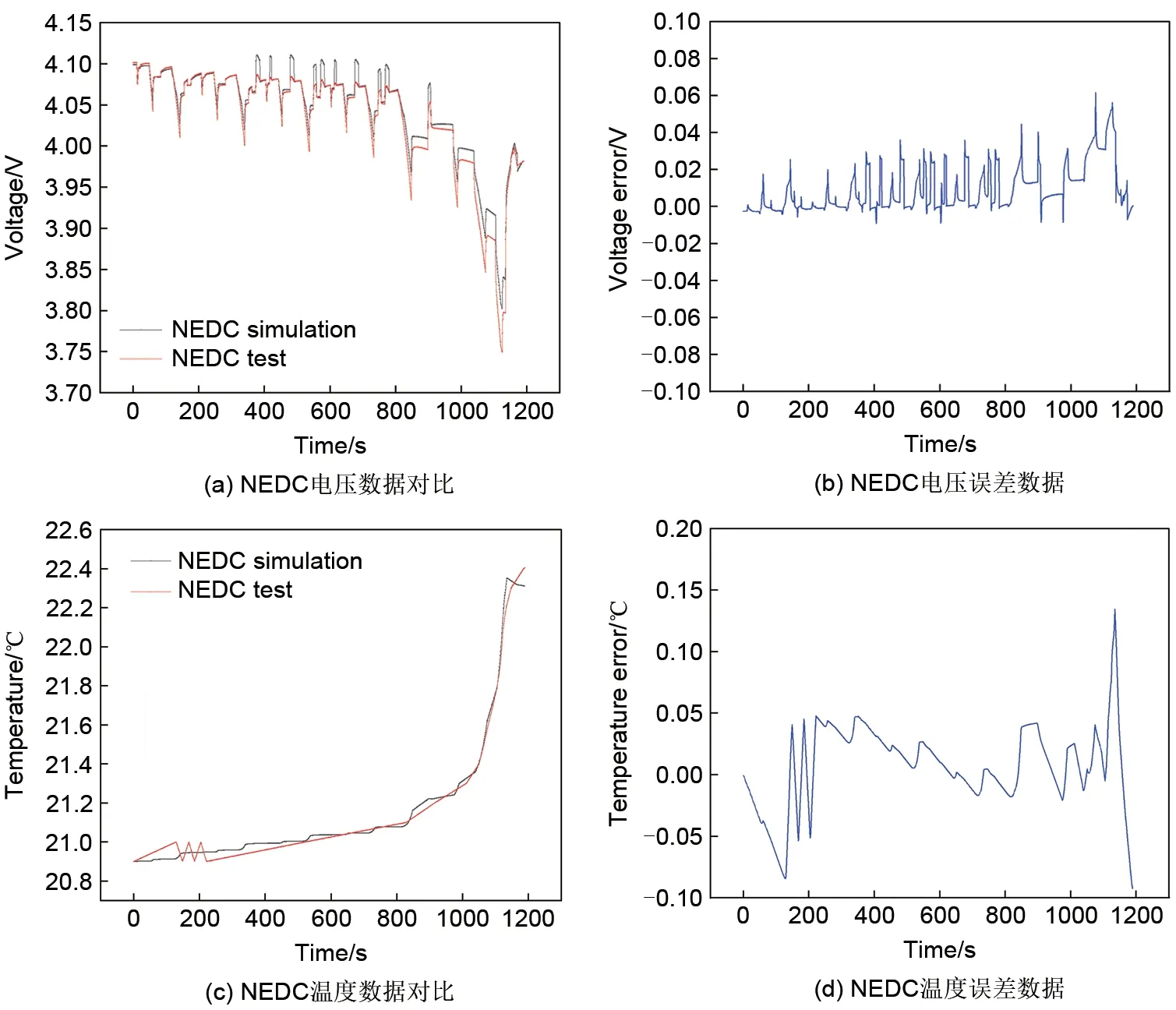
图12 常温NEDC工况下仿真模拟与实验数据对比及其误差情况Fig.12 Comparison of simulation and experimental data under normal temperature NEDC conditions and their error

电压仿真最大误差仅有61.5 mV，可见等效电路模型在10～55 ℃范围内，对于NCM 电池在0.33～1 C 倍率工况下预测精度较为准确；且NЕDC工况也存在很多倍率范围外的电流工况，电压预测精度也较准确；温度预测温升约16 ℃，最大温度误差在0.15 ℃以内，电压预测精度较为可观。由此可见，等效电路-热模型对于模拟52 Ah的NCM 电芯具有研究的实际意义，且整体预测精度较高。