基于梯度孔隙率金属泡沫的复合相变单元储热性能数值模拟
2023-08-29严景好李一鸣孙小琴席丽娜姜昌伟
严景好,李 杰,李一鸣,孙小琴,席丽娜,姜昌伟
(长沙理工大学能源与动力工程学院,湖南 长沙 410114)
近几十年来,随着化石能源消耗的急剧增加,环境污染及可持续发展问题日益凸显,人类对量大、清洁且可循环使用的可再生能源的需求日益增大。然而,在实际应用过程中,以太阳能、风能、水能等为主的可再生能源存在空间和时间供需不匹配问题。鉴于此,通过开发高效储能设备,可以有效降低供需间的不匹配,且能够提高能源系统性能和可靠性,在能源结构转型方面发挥着重要作用[1]。
储能包括化学储能、潜热储能及显热储能等,其中,涉及固液相变的潜热储能技术(LHTЕS)由于具有高储能密度和储能过程等温等优点,在建筑节能[2]、航天电子器件冷却[3]、太阳能集热器[4]、工业废热回收[5]和电池热管理技术[6]等各种能源领域应用潜力十分广阔。其中,石蜡由于其便宜、化学性质稳定、无腐蚀性等优点,是被广泛使用的相变材料之一。但是,石蜡也存在导热系数低等缺点,这严重影响了潜热储能系统的储热效率和温度均匀性。为实现相变储能系统的高效传热与快速储能,研究人员常在石蜡中加入各种高导热材料,包括添加纳米颗粒[7]、嵌入导热翅片[8]和填充金属泡沫[9]等。其中,金属泡沫-相变材料(石蜡)复合储能系统由于具有高导热率、大孔隙比表面积、强紧凑性等优点,能够实现热量快速传递和储热密度有效增加,成为当前储能系统强化传热的重要途径[10]。
在针对金属泡沫-石蜡复合储能系统的凝固熔化性能研究中,通过分析金属泡沫复合相变材料的传热特性可知,金属泡沫对复合相变材料的温度场影响很大,通过构造非均匀金属泡沫形成的非均匀温度场,可以对系统整体的自然对流产生影响,鉴于此,诸多学者提出了梯度孔隙率金属泡沫/石蜡复合相变材料概念。Zhang 等[11]分别对均匀孔隙率为0.859、0.913、0.958 以及随高度在0.859~0.958 范围内的梯度变化结构进行三维数值模拟研究。结果表明,金属泡沫孔隙度梯度变化结构不仅可以有效避免熔化过程中的底角残留,还能加速熔化速率。梯度孔隙率金属泡沫的熔化速率比均匀金属泡沫高173%以上。Xu等[12]对部分填充多孔介质的水平同心管蓄能(TЕS)单元进行了数值研究,结果表明,多孔介质填充在底部时PCM 的熔化性能提高最佳,多孔介质的最佳填充高度比为0.7。在该结构下,与无孔情况相比,TЕS速率密度可以显著提高6倍以上。Joshi等[13]通过数值模拟方法研究了在部分填充金属泡沫的系统中,泡沫填充高度比、孔隙率、梯度孔隙率对复合材料熔化性能的影响。结果表明,填充高度比越大,储存能量的时间越短,储能能力越强。相同填充比条件下,孔隙率越小,熔化时间越短,储能能力越强。与底部填充均匀孔隙率金属泡沫相比,底部填充梯度孔隙率金属泡沫的完全熔化时间可以减少10%。Yang 等[14]通过实验研究了孔隙率、孔隙密度和金属泡沫导热系数梯度(不同材料的金属泡沫组合)对金属泡沫饱和水凝固界面演化的影响。结果表明,对于给定孔隙密度的金属泡沫,与均匀孔隙率和负梯度孔隙率结构相比,正梯度孔隙率结构能有效加速饱和水的固液界面演化进程;孔隙密度负梯度分布能够显著提高凝固速率;将具有较高导热系数的金属(例如Cu)组成的泡沫放置在冷却边界附近,将导致相变的进一步增强。宋瀚文等[15]对金属泡沫填充量为15%的复合相变材料蓄热过程进行实验研究。结果表明,金属泡沫填充在底部强化了底部导热能力,缩短了整体熔化时间。相比于纯石蜡,总熔化时间缩短了3.44%。
从以上文献可知,学者们大多针对高孔隙率(孔隙率为0.8~0.99)金属泡沫结构下的复合相变材料进行研究,对于金属泡沫结构为低孔隙率时(孔隙率为0.6~0.8)则研究较少;此外,大部分研究中梯度孔隙率的结构构造简单,对梯度孔隙率作用下的自然对流影响研究较少,因为低孔隙率金属泡沫具有较大的流动阻力和温度均匀性,其自然对流效应较弱。低孔隙率金属泡沫/石蜡复合相变材料因具备较高的有效导热率在热能储存系统中得到广泛应用[16],对低孔隙率金属泡沫进行梯度孔隙率结构设计,材料内部的有效导热系数差异增大,熔化周期后期的温度分布的不均匀性增强,从而,梯度孔隙率结构对自然对流效应的提升效果最佳。因此,有必要对低孔隙率金属泡沫复合相变材料的传热性能展开研究。本工作通过数值模拟方法研究低孔隙率金属泡沫/石蜡复合相变材料的传热性能,并对低孔隙率金属泡沫进行梯度孔隙率结构设计,分析不同梯度结构金属泡沫/石蜡复合相变材料的熔化机理及熔化率曲线、完全熔化时间、储能量(TЕS)、储能速率(TЕSR)等参数,构造出能强化传热的复合相变储能结构,为低孔隙率金属泡沫结构下的潜热储能系统设计提供理论指导。
1 物理模型与控制方程
1.1 物理模型
本工作采用经典二维矩形腔结构模型[17],如图1(a)所示,此实验中复合相变材料由铝金属泡沫和石蜡构成,其中,铝金属泡沫的孔隙密度为10 PPI,孔隙率为0.75,石蜡型号为具有较低熔点和较高潜热的石蜡R56,表1 展示了铝金属泡沫和石蜡R56的热性能参数。复合相变储能系统矩形尺寸为60 mm(长)×45 mm(高),底部加热且恒定热流大小为3500 W/m2,其余边界用保温材料包裹,可视为绝热边界条件。基于文献[18]构造的几何模型,本工作提出了一种新的梯度孔隙率金属泡沫结构,该结构均分为3 个不同孔隙率的对称区域[图1(b)~(c)],每个区域具有均匀孔隙率。该结构相对于现有的垂直分层结构,能够形成一侧中间温度高,两侧温度低的温度分布,因此更容易形成自然对流。根据孔隙率的分布情况,将梯度孔隙率泡沫金属结构分为负梯度结构和正梯度结构,正梯度结构是指孔隙率沿热流方向增加,如图1(b)所示,负梯度结构是指孔隙率沿加热方向减少,如图1(c)所示,为了保证相变材料总体积相等,梯度孔隙结构和均匀孔隙结构的平均孔隙率均为0.75。此外,本工作选取孔隙率梯度分别为0.02、0.04、0.06、0.08、0.1、0.12 进行数值研究,对比不同梯度孔隙率结构与均匀孔隙率结构的换热特性。本工作研究的金属泡沫构型见表2,其中,ε1-ε2-ε3 是孔隙率沿热流方向的分布情况,S0 是均匀孔隙率结构,S1-1到S1-6是孔隙率负梯度分布结构,S2-1到S2-6是孔隙率正梯度分布结构。
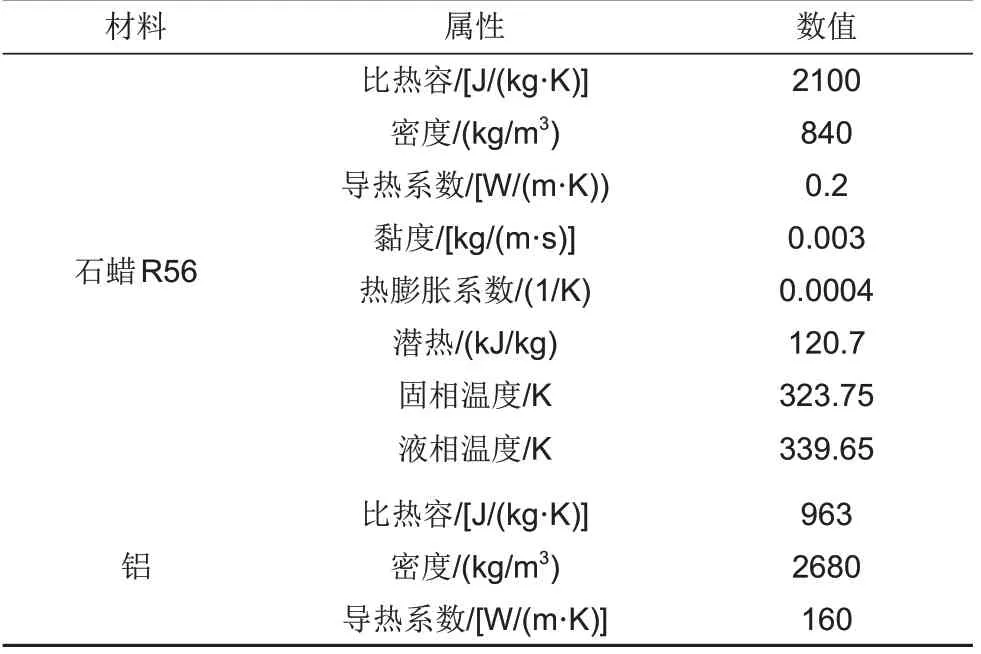
表1 石蜡和铝泡沫的热物理性质[17]Table 1 Physical properties of paraffin and aluminium foam
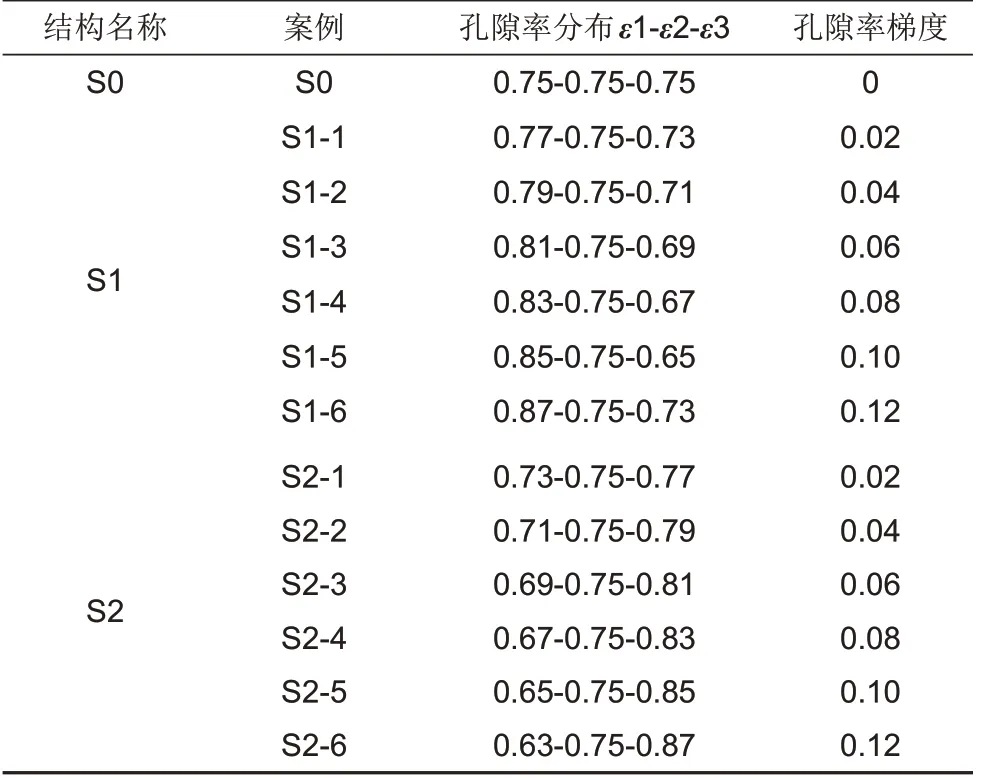
表2 本工作研究的金属泡沫构型Table 2 Structural parameters of metal foam considered in this paper
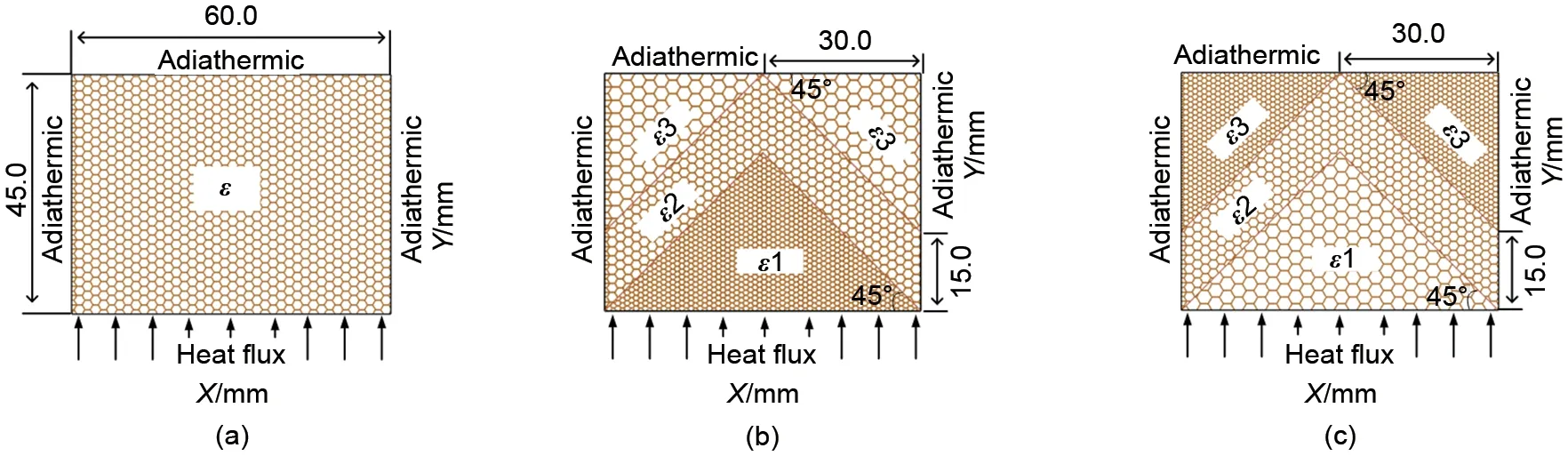
图1 物理模型和边界条件Fig.1 Physical model and boundary condition
1.2 数学模型
金属泡沫/石蜡复合相变材料的熔化过程较为复杂,涉及金属泡沫的导热过程、金属泡沫与石蜡之间的耦合传热过程、固态石蜡导热及其熔化后的自然对流传热过程等,为简化模型,本工作做出如下假设:①流体流动为层流;②不考虑熔化过程中的体积变化,液态石蜡密度满足Boussinesq假设;③液相视为不可压缩流体。具体控制方程如下。
1.2.1 流体动力学方程
连续方程:
动量方程采用Darcy-Brinkman模型,x方向和y方向动量方程如下[19]:
公式(2)、(3)中的Su和Sv是源项,计算公式是(4)和(5)。公式(4)和(5)中,等式右边第一项用于描述固-液相界面对动量方程的影响[20],其中,Amush是糊状区常数,本工作设置为105 (kg·m3)/s;δ是一个极小的数,通常设置为0.0001,目的是为了防止这一项除以0;γ是PCM 的熔化率,只与温度有关,由公式(6)计算;右边第二项和第三项分别是多孔介质引起的黏性阻力项和惯性阻力项,K是渗透率,由公式(7)~(9)计算[21-22];C是惯性系数,由公式(10)计算[23];其中,ω是孔隙密度,本工作取值为10 PPI;dp是金属泡沫的孔径;df是金属泡沫的纤维直径;公式(5)右边第四项是自然对流对动量方程的影响,α是热膨胀系数;Tref是参考温度,本工作设置为293 K。其余符号表示为:PCM密度(ρl)、x方向速度(ul)、y方向速度(νl)、压力(p)、时间(t)。
1.2.2 传热方程
为了更准确地计算复合材料内部的传热,本工作能量方程使用两方程模型[23],该模型假设金属泡沫和PCM温度是非热平衡的,此时则有:
PCM能量方程:
金属泡沫能量方程:
在公式(11)和(12)中,asf是金属泡沫的界面面积之比,由公式(13)计算;hsf是金属泡沫与PCM之间的界面传热系数,由公式(14)~(16)计算。其余符号表示为:孔隙率(ε)、PCM比热容(cl)、PCM温度(Tl)、相变潜热(L)、金属泡沫密度(ρm)、金属泡沫热容(cm)、金属泡沫温度(Tm)、PCM 导热系数(kl)、金属泡沫导热系数(km)。
在本研究中,由于梯度结构中金属泡沫的孔隙率的差异,不同区域需要设置不同的参数。因此在表3中统计了本工作所使用的孔隙参数。
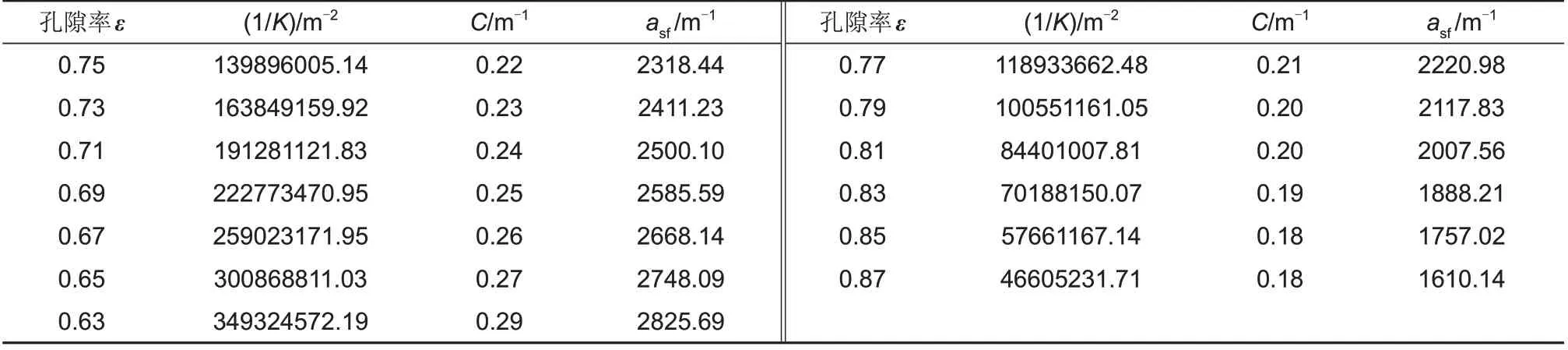
表3 本工作使用的孔隙参数Table 3 Pore parameters used in this paper
1.2.3 初始条件和边界条件
初始阶段,石蜡是固态且与金属泡沫具有相同温度(293 K),整个熔化过程中,底部被大小为3500 W/m2的恒定热流进行加热,忽略熔化过程中的热损失,其余壁面为绝热边界条件,初始条件和边界条件表述如下:
初始条件:0≤x≤60 mm,0≤y≤45 mm,Tl=Tm=293 K,ul=νl=0;
边界条件:0≤x≤60 mm,y=0,ql=3500εW/m2,qm=3500(1-ε) W/m2
2 数值方法与模型验证
2.1 数值方法
控制方程求解使用ANSYS Fluent 2022 求解器,压力和速度耦合使用PISO 算法,压力项使用PRЕSTO!法离散,对流项使用二阶迎风格式离散,非稳态项的计算使用二阶隐式,压力、动量和能量的松弛因子分别为0.3、0.7 和1,连续方程、动量方程和能量方程的残差标准分别为10-3、10-3、10-6,同时,设置单个时间步长内迭代步数不低于60步。
为了验证本工作数值模型的准确性,选用均匀孔隙率结构S0研究熔化过程中PCM的熔化率演变过程。为了验证网格无关性,网格数量分别为8800、45000 和80000,对应时间步长均为0.05 s,不同网格数量计算得到对应的熔化率随时间变化如图2所示,可以看出,网格数为45000计算结果与密网格数80000时结果完全一致,故本工作计算网格数取45000 个,其中,网格尺寸是0.024 mm,网格类型是结构网格;为了验证时间步长的无关性,时间步长分别取为0.02 s、0.05 s和0.1 s,对应的网格数量均为45000,不同时间步长对应的熔化率随时间变化如图3所示,可以看出,当时间步长减小到0.05 s以下后,改变时间步长对熔化率曲线的影响很小,故本工作的数值计算时间步长均设置为0.05 s。
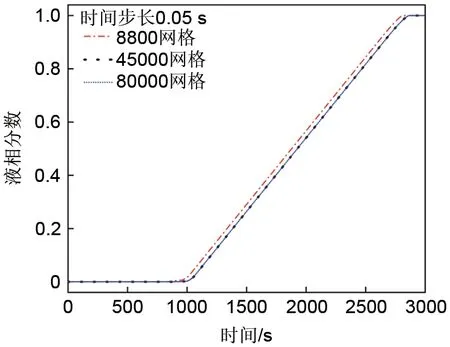
图2 不同网格数量的熔化率曲线比较Fig.2 Comparison of melting fraction curves for different mesh quantities
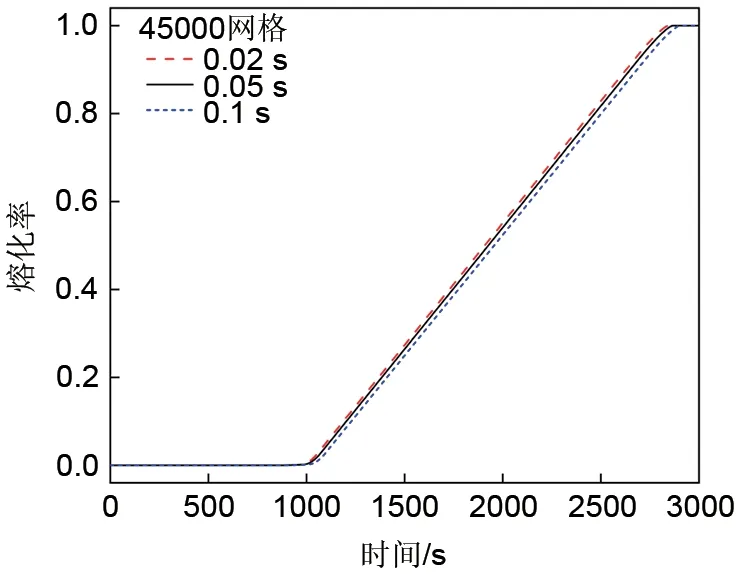
图3 不同时间步长的熔化率曲线比较Fig.3 Comparison of melting fraction curves for different time steps
2.2 模型验证
在Hu 等[17]的实验中,详细给出了孔隙率为0.75且孔隙密度为10 PPI时的3个监测点数据,其位置分别是TC#1(x=30 mm,y=10 mm),TC#2(x=30 mm,y=20 mm)和TC#3(x=30 mm,y=30 mm)。本工作对比了3个监测点的数值计算和实验测量温度值,热电偶位置以及对比结果如图4所示。可以看出数值计算与实验测量吻合较好(最大相对误差为1.3%),表明本工作数值模型可以用于后面的数值研究。同时,由于梯度孔隙率结构中金属泡沫的孔隙率和间隙传热系数hsf等参数也是梯度变化,故本工作编制了相应UDF(user defined function),用来计算梯度孔隙率结构中金属泡沫的孔隙率和间隙传热系数hsf等参数,为验证程序的正确性,本工作对文献[18]提出的水平梯度孔隙率结构H3-5进行了数值计算,其熔化率对比结果如图5、图6 所示。可以看出,本工作数值计算结果与文献中的参考结果一致,验证了本工作编制UDF的准确性。
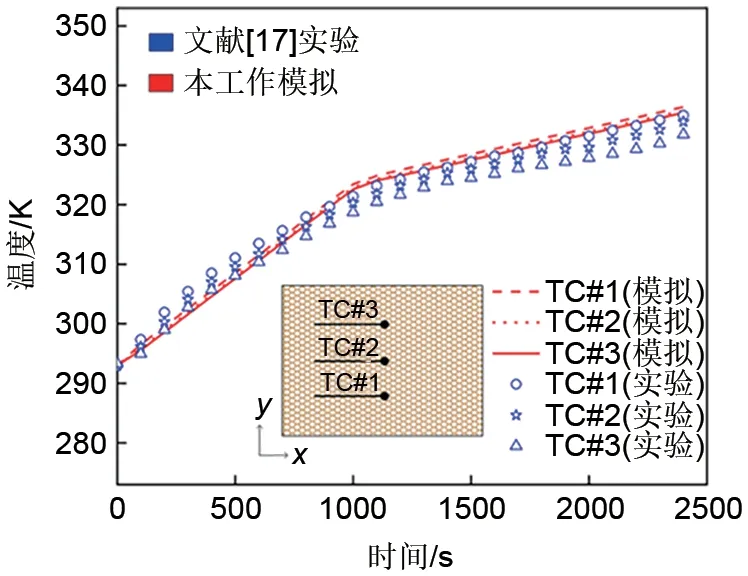
图4 与Hu等[17]实验的温度比较Fig.4 Comparison with the temperature of the experiment results in reference [17]
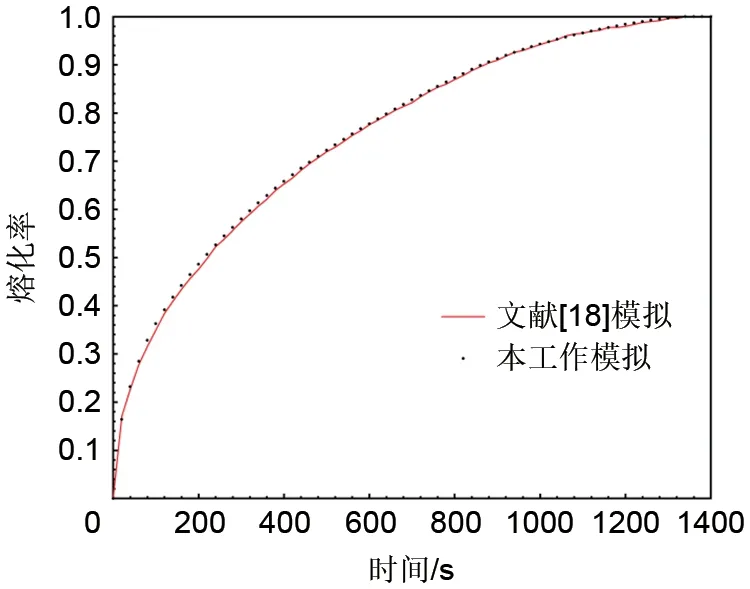
图5 与文献[18]的数值研究结果的熔化率对比Fig.5 Comparison with the melting fraction of the numerical results in reference [18]
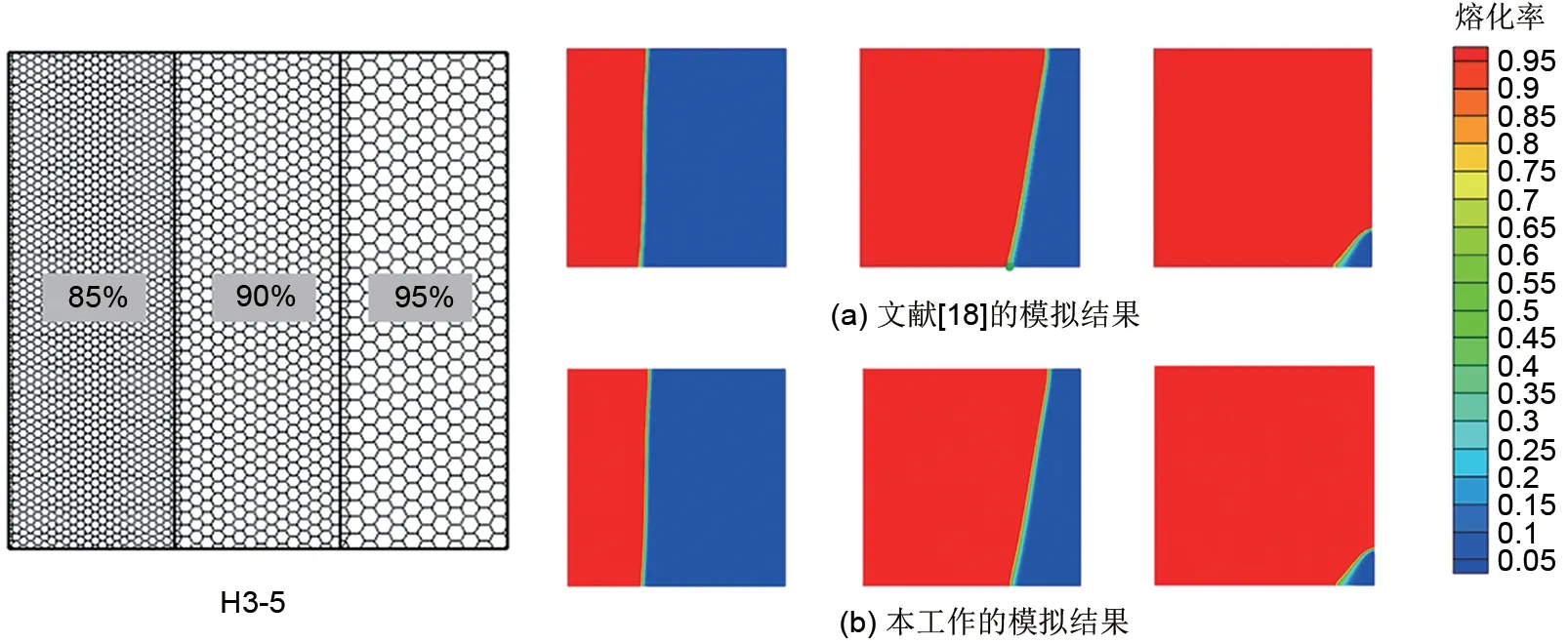
图6 与文献[18]的数值研究结果的熔化相界面对比Fig.6 Comparison with the melting-phase interface of the numerical results in reference [18]
3 结果与讨论
3.1 孔隙率负梯度分布对熔化过程的影响
为研究金属泡沫孔隙率沿加热热流方向负梯度分布对复合相变材料熔化过程的影响,本部分对比了构型S1-1、S1-2、S1-3、S1-4、S1-5、S1-6 和均匀孔隙结构S0的熔化过程,3.1.1节对比分析了熔化过程中各构型的PCM熔化率演变情况,3.1.2节对各构型储热性能进行了评价。
3.1.1 PCM熔化率的演变
图7 是构型S1-1 至S1-6 和S0 的PCM 熔化率随时间变化的曲线,可以看出,在1000 s 之前,七种构型对应的PCM 均无明显熔化,通过分析可知,本工作采用的金属泡沫孔隙率较低,金属泡沫占比较多,金属泡沫的高导热性使热量快速导入复合相变材料内部,而不会在加热面附近聚集,所以前期PCM 熔化不明显;熔化开始以后,负梯度孔隙率结构的熔化速度明显比均匀孔隙率结构的熔化速度快,熔化速度情况见表4,可以看出,同一时刻,梯度孔隙率结构的熔化率均高于均匀孔隙率结构,本工作构造的负梯度孔隙率结构可以有效加快复合材料的熔化速度,此外,随着孔隙率梯度增加,传热性能增强程度越大。
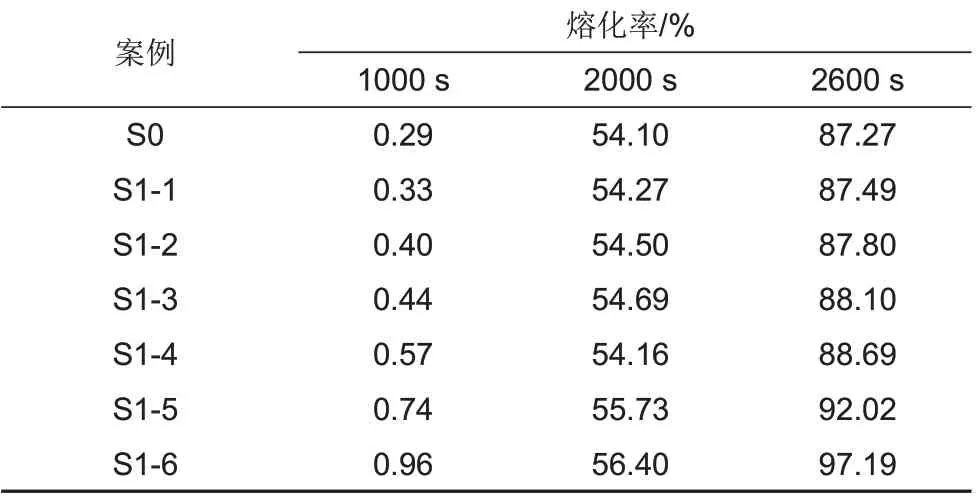
表4 不同时刻的熔化率统计Table 4 Melting fraction statistics at different moments
为了分析复合相变材料受热熔化的演化进程,本小节比较了不同构型在不同时刻的熔化相界面,其对比结果如图8所示。可以看出,对于均匀孔隙率结构,液相率界线呈水平分布,而在本工作构造的负梯度孔隙率结构中,在熔化周期的前期阶段(1000 s时刻),液相率界线呈现中间上凸,两端下凹趋势,且随着孔隙率梯度增加,这一趋势更为明显,分析可知,这是由于两侧孔隙率较低,更多热量通过金属泡沫导入结构上部,导致两侧下部区域熔化较慢,这说明,孔隙率负梯度的分布,相比于均匀孔隙结构,在前期增加了PCM 的熔化数量;在熔化周期的后期阶段(2600 s时刻),负梯度孔隙率结构液相率界线呈现两侧上凸,中间下凹趋势,且随着孔隙率梯度增加,两侧上凸趋势更明显,这是因为在复合相变材料上部,两侧金属泡沫孔隙率低,金属泡沫传递热量更多且此处PCM含量更少,由此导致两侧熔化加快。综合来看,在熔化周期的不同阶段,负梯度孔隙率对复合材料的传热均有不同程度增强,从而有效加快复合相变材料的熔化速度。
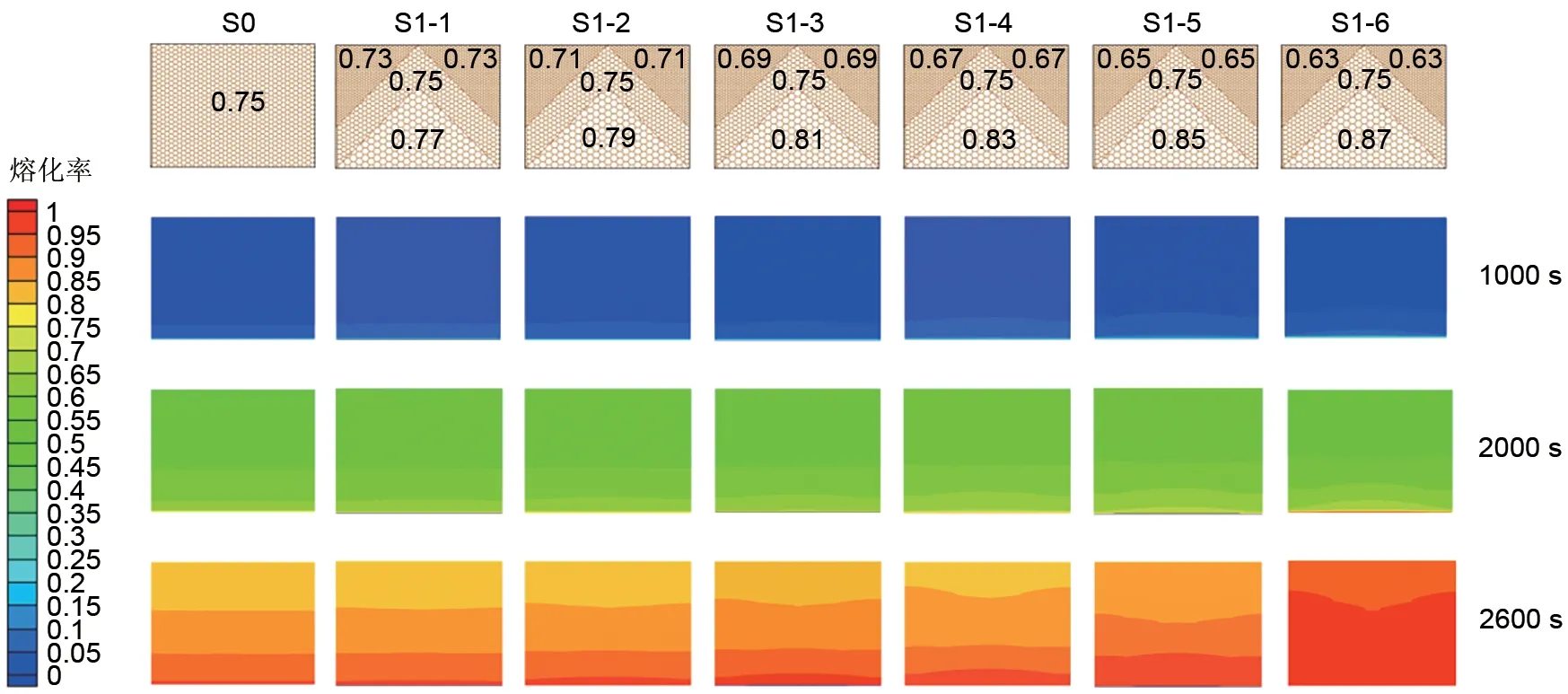
图8 孔隙率负梯度分布结构的熔化相界面Fig.8 Melting-phase interface of a negative porosity gradient distribution structures
此外,为证明本工作提出的梯度孔隙率结构相对当前已有结构具有优势,本工作将最优的负梯度孔隙率结构S1-6与文献[18]提出的垂直梯度孔隙率结构V3 进行对比,熔化率对比如图9 所示。可以看出,相对于均匀孔隙率结构,结构S1-6和V3均能加快材料的熔化速度。然而,在熔化开始2100 s左右,结构S-6的熔化速率急剧增加,超过V3。分析认为,结构S1-6 相比于V3,在熔化后期温度分布更不均匀,所以在V3 自然对流效应减弱以后,S1-6结构的自然对流效应仍会进一步增强。最终,S1-6 结构比V3 结构提前完成熔化过程。因此,本工作提出的结构相比当前已有研究更适用于相变蓄热单元。
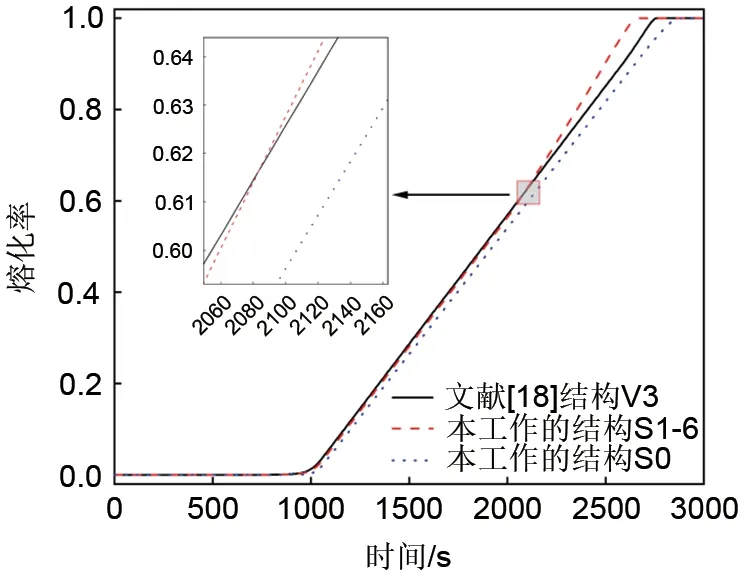
图9 与文献[18]结构V3的熔化率对比Fig.9 Comparison with the melting fraction of the V3 in reference [18]
3.1.2 储热性能的评价
在相变潜热储能系统(LHTЕS)中,储热性能的提高可以有效提高系统经济性[24]。本节综合评价了负梯度孔隙率结构复合相变材料的完全熔化时间,热能储存量(thermal energy storage,TЕS)和热能储存速率(thermal energy storage rate,TЕSR),其中,TЕS[式中E(t)]由公式(17)计算,TЕSR[式中P(t)]由公式(18)计算。其中,Tave,l和Tave,m分别是在完全熔化时刻PCM 和金属泡沫的平均温度,ttot是完全熔化时间,Tin是初始温度,设置Tin为293 K,mm和ml分别是金属泡沫和石蜡的质量。
图10记录了熔化完成时,构型S1-1至S1-6和S0 对应的金属泡沫平均温度、PCM 平均温度以及热能储存总量。可以看出,金属泡沫和PCM 的平均温度存在一定差异,表明本工作利用能量双方程模型考虑金属泡沫和PCM 间的热不平衡状态是合理的。此外,系统的TЕS与相变材料的平均温度呈现正比例关系。综合对比可知,相比于均匀孔隙率结构,负梯度孔隙率结构可以提高系统的TЕS,且随着孔隙率梯度的增加,TЕS提高更为显著,负梯度孔隙结构最高可以使TЕS提高0.15%。
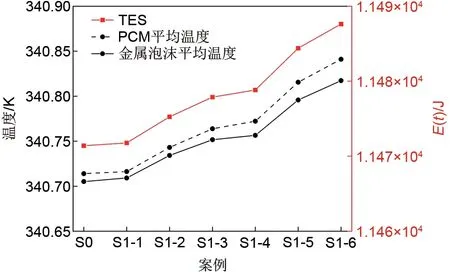
图10 孔隙率负梯度分布结构的TES和平均温度Fig.10 TES and average temperature of porosity negative gradient distribution structures
针对构型S0以及S1-1至S1-6对应的完全熔化时间和储能速率如图11 所示。完全熔化时间分别为2865 s、2853 s、2826 s、2802 s、2781 s、2732 s、2656 s。可以看出,负梯度孔隙结构相比均匀孔隙率结构可以有效缩短熔化时间,且随着孔隙率梯度的增加,熔化时间缩短越多,最高可以缩短7.32%(S1-6构型);此外,负梯度孔隙结构可以提高系统的TЕSR,且随孔隙率梯度增大,TЕSR提高越显著,负梯度孔隙结构可以使TЕSR最高提高8.02%(S1-6构型)。
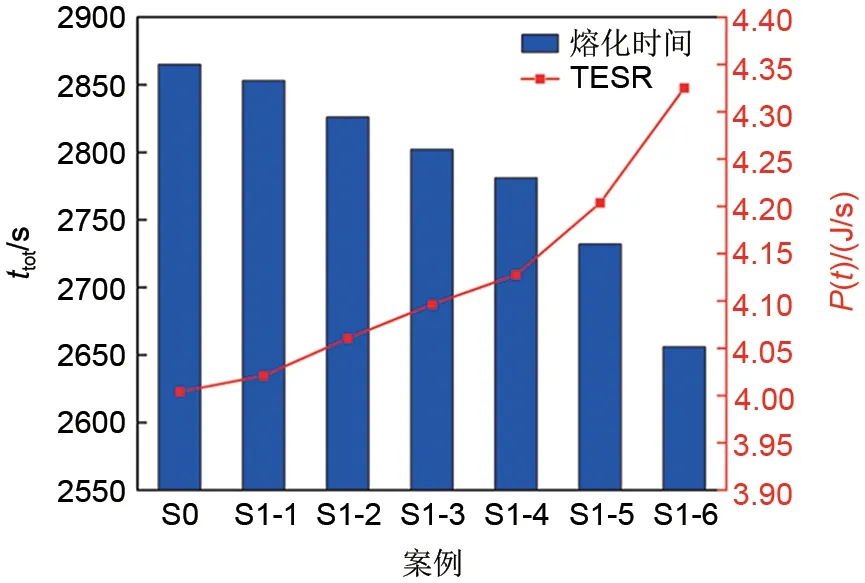
图11 孔隙率负梯度分布结构的TESR和完全熔化时间Fig.11 TESR and Complete melting time of porosity negative gradient distribution structures
3.2 孔隙率正梯度分布对熔化过程的影响
为研究金属泡沫孔隙率沿加热热流方向正梯度分布对复合材料熔化过程的影响,本部分对比了构型S2-1、S2-2、S2-3、S2-4、S2-5、S2-6 和均匀孔隙结构S0的熔化过程,3.2.1节分析了在熔化过程中PCM熔化率的演变规律,3.2.2节对它们的储热性能进行了对比评价。
3.2.1 PCM熔化率的演变
图12 是构型S0、S2-1 至S2-6 的PCM 熔化率随时间变化曲线。可以看出在熔化前期,孔隙率正梯度分布结构和均匀孔隙率结构的熔化率曲线几乎完全重合;仅在熔化后期,孔隙率正梯度分布结构熔化速率稍有促进,且整体熔化速度对比结果满足:S2-5>S2-3>S2-6>S2-4>S2-2>S2-1>S0,综合来看,与孔隙率负梯度分布相比,孔隙率正梯度分布对复合相变材料熔化性能的增强作用有限。
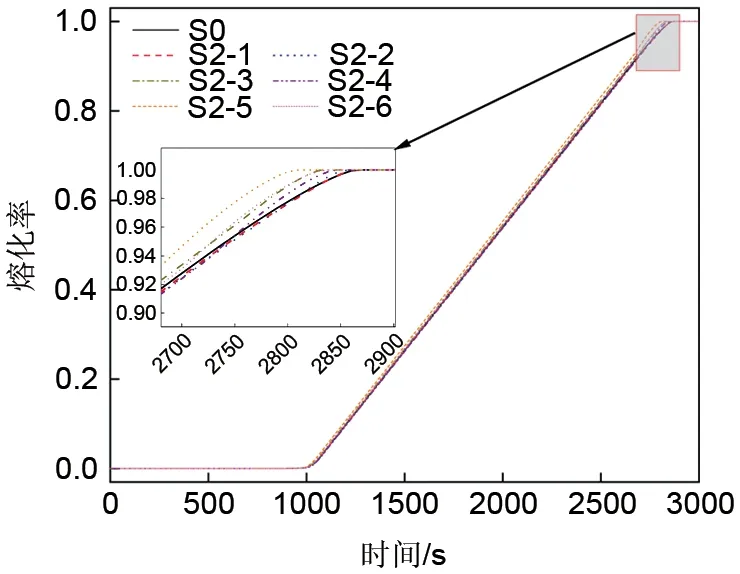
图12 孔隙率正梯度分布结构的熔化率变化Fig.12 Changes in melting fraction of porosity positive gradient distribution structures
图13 比较了1000 s、2000 s、2600 s 时,构型S0、S2-1至S2-6的熔化相界面。可以看出,在熔化前期,孔隙率正梯度结构的PCM 熔化率比均匀孔隙率的少,固液界限从中间向下凹陷,这是因为,在热源附近,中间部分的泡沫金属占比大于侧面,中间部位的热量被快速导入内部,无法集中在热源附近,导致熔化前期中间部位的PCM 熔化量比侧面少,而在熔化后期,则会使固液界限中间部位向上凸起,综合来看,正梯度孔隙结构的熔化速度比均匀孔隙率结构更快,但其促进作用较弱。熔化率统计见表5,可以看出,正梯度构型中熔化速度最快的是构型S2-5。
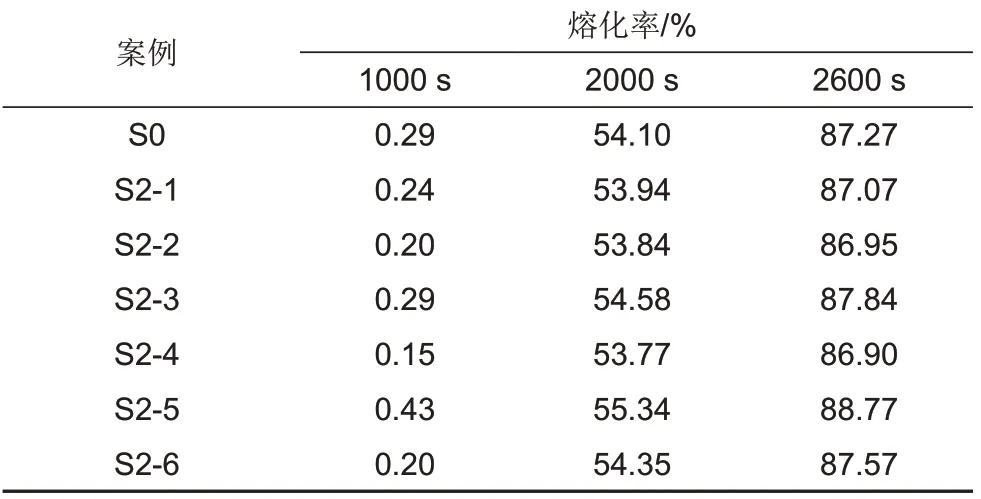
表5 不同时刻的熔化量统计Table 5 Melting fraction statistics at different moments
3.2.2 储热性能的评价
图14 记录了熔化完成时,构型S0、S2-1 至S2-6 对应的泡沫金属和PCM 的平均温度及热能储存总量。与负梯度孔隙率结构一样,正梯度孔隙率结构的TЕS 与相变材料的平均温度呈正比例关系;不同的是,对于相同的孔隙率梯度,正梯度孔隙率结构比负梯度结构的平均温度高,熔化完成时储存的能量更多;总体来看,相比于均匀孔隙率结构和负梯度孔隙率结构,正梯度孔隙结构熔化完成时TЕS更高,且随着孔隙率梯度的增加而增加。综合对比可知,正梯度孔隙率结构TЕS 最高的是构型S2-6,可提升0.49%。
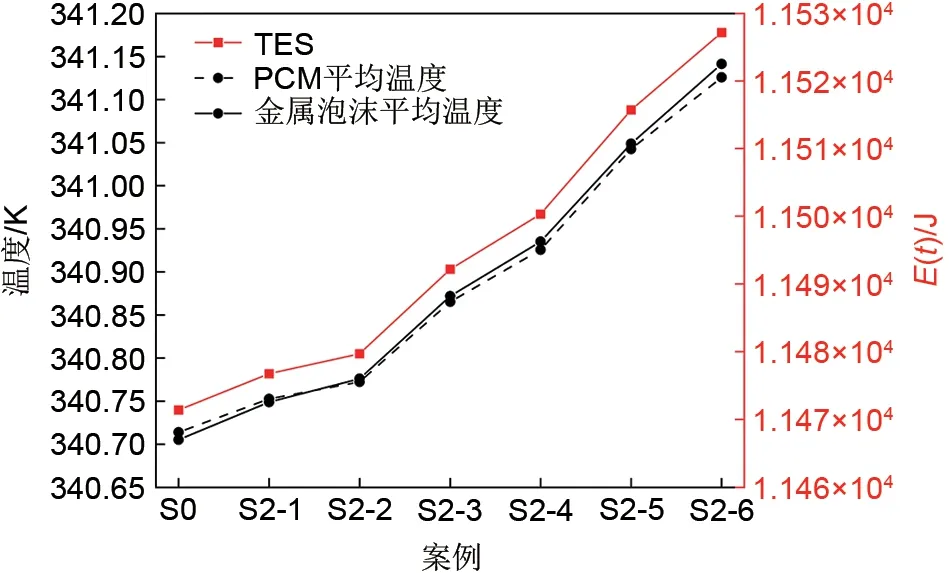
图14 孔隙率正梯度分布结构的TES和平均温度Fig.14 TES and average temperature of porosity positive gradient distribution structures
图15 对比了构型S0、S2-1 至S2-6 的完全熔化时间和TЕSR,其完全熔化时间分别为2865 s、2862 s、2855 s、2834 s、2847 s、2811 s、2839 s,可以看出,与均匀孔隙率相比,正梯度孔隙结构的熔化时间没有明显减少,储存热能则有所增加。综合来看,与均匀孔隙率结构相比,正梯度孔隙结构的TЕSR有所增加,但增加幅度明显弱于负梯度孔隙率结构,TЕSR 最高的正梯度孔隙结构构型是S2-5,其提高幅度为1.42%。
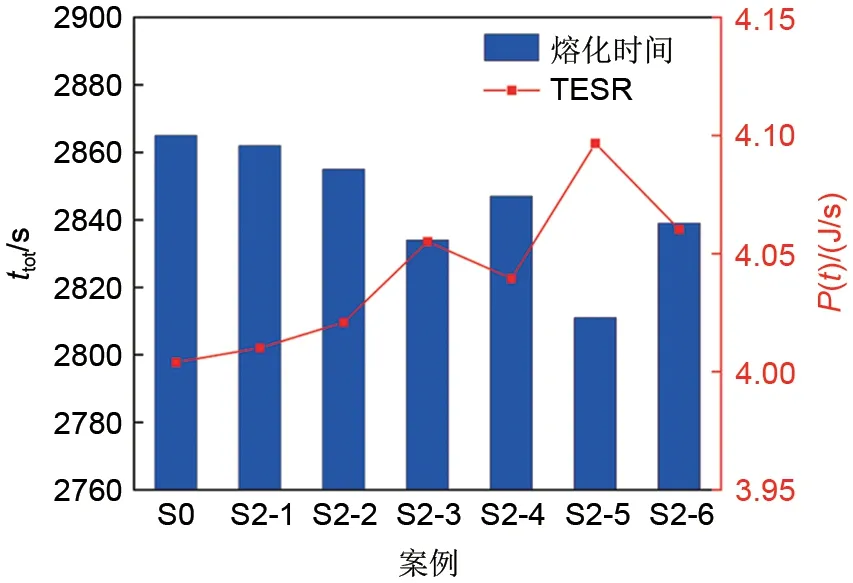
图15 孔隙率正梯度分布结构的TESR和完全熔化时间Fig.15 TESR and Complete melting time of porosity positive gradient distribution structures
4 结论
本工作提出了一种新的梯度孔隙率结构,分别研究了孔隙率沿加热热流方向负梯度分布和正梯度分布时,具有不同孔隙率梯度的复合相变材料的传热性能和储热性能。通过分析得到以下结论。
(1)与均匀孔隙率泡沫金属相比,填充梯度孔隙率泡沫金属结构可以进一步改善复合相变材料的储热性能;
(2)与均匀孔隙率结构相比,填充正梯度孔隙率泡沫金属的复合相变材料熔化速度没有明显增加,但其储能量(TЕS)相比于均匀孔隙率结构能提高0.49%,稍优于负梯度孔隙率结构;
(3)与均匀孔隙率结构和正梯度孔隙率相比,填充负梯度孔隙率泡沫金属的复合相变材料熔化速率增大明显,且其提升幅度随着孔隙率梯度的增加而增大。相比均匀孔隙率结构,其完全熔化时间最高可减少7.32%,TЕS 最高可提高0.15%,TЕSR最高可以提高8.02%。
