改进随机抽样一致性算法在建筑物现状测量中的应用

2023-08-29黎建洲韩贤权

长江科学院院报 2023年8期

黎建洲,韩贤权,万鹏

(1.长江科学院工程安全与灾害防治研究所,武汉 430010;2.水利部水工程安全与病害防治工程技术研究中心,武汉 430010;3.国家大坝安全工程技术研究中心,武汉 430010)

0 引言

传统的建筑物现状测量主要利用全站仪和实时动态载波相位差分技术(Global Navigation Satellite SysteM-Real-time kinematic,GNSS-RTK)测量特征点,配合测距仪和钢卷尺等,该方法工作强度大、效率低、对测量环境要求严格,而且得到的测量信息比较单一[1]。工程项目施工过程可能造成周围地质条件变化,引起地表不均匀沉降变形,导致建筑物发生倾斜、开裂等破坏,需要及时掌握施工过程中建筑物的变形情况,客观记录建筑物状态。目前,建筑物变形测量主要采用上述传统测量方法,在实际测量中因其效率低会影响工程进度,无法及时掌握建筑物的变形情况,存在安全隐患。三维激光扫描技术通过逐点扫描的方式获取高密度激光点云数据,通过有效处理可提取研究对象精确的三维几何信息[2]。相比传统的单点式测量方法,三维激光扫描技术数据采集效率高,能够获取目标的面状变形信息,可以对建筑物进行整体监测,能有效避免以往基于单点数据的变形分析结果中所带有的局部性和片面性,因此是进行地表建筑变形监测的一种新的技术手段[3]。

胡玉祥等[4]成功将三维激光扫描技术应用于建筑物的竣工测量;钟棉卿[5]、倪佳琦[6]、彭劲松等[7]、梁智勇等[8]分别利用三维激光扫描技术完成了建筑物立面测量工作,结果证明该技术能够大大地提高工作效率,具有广泛的应用前景。李玉兵[9]提出了一种根据建筑物立面特征规则的建筑物立面分割方法,实验表明该方法具有较强的适用性和鲁棒性。在具体实施过程中,冯鸣等[10]使用改进的最近点迭代(Iterative Closest Point,ICP)算法对岩体结构点云与影像进行了配准,从而获得了整个研究对象的结构面点云;韩贤权等[11]提出了新的适应度函数以改进粒子群优化(Particle Swarm Optimization,PSO)算法,该适用度函数使得点云数据法向量叉积代数和最小,在选取最佳配准点的基础上实现了散乱点云的精确配准。随机抽样一致性(Random Sample Consensus,RANSAC)算法是点云平面识别的常用算法,针对RANSAC算法在处理含有无效数据时的有效性,众多学者将其应用于平整结构面识别研究。Han等[12]在其研究中对RANSAC算法进行了改进和优化,证明了其在岩体结构面识别方面的可行性,但在研究中发现,当点云数据量较大时,其处理效率还有待提高;肖娇琳等[13]基于RANSAC算法,提出建筑物平面和曲面优化拟合算法,实验表明该算法能够较好地识别噪点数据,抗干扰性较强。

本文在前人研究基础上,针对传统RANSAC算法在建筑物平面拟合过程中存在的问题,提出了改进随机抽样一致性(Modified RANSAC,M-RANSAC)算法进行平面和边缘探测,并将该方法成功应用于珠江三角洲水资源配置工程的建筑物现状测量。

1 改进随机抽样一致性算法

1.1 RANSAC算法

RANSAC算法是一种以迭代方式从一组包含离群点的数据中估算出数学或几何模型的算法。常规RANSAC算法的主要步骤为：

(1)从点云数据中随机选取3个非共线点,计算通过这3点构成的平面方程。

(2)利用得到的平面方程,计算所有点到平面距离,找出位于阈值内的内点。

(3)如果内点个数大于设定阈值(通常为总点数的50%～70%),则认为找到了主要的平面成分,算法结束。否则,返回步骤(1)继续迭代。

(4)根据内点重新计算平面方程,获得优化后的平面模型。

(5)对优化后的平面模型,再进行验证,计算所有点到新平面距离,找出新的内点集。如果内点集与上一步内点集差异很大,则表明上一步选择的种子点不够理想,需要重新选择种子点并重复步骤3。

(6)最终获得的平面模型及对应的内点集为主要的平面成分及对应的特征点集。

(7)从原点云数据中剔除得到的平面内点,得到剩余未处理的点,重复步骤1—步骤6,继续搜索其他的平面成分。

(8)反复进行搜索迭代,直到剩余的点数量低于阈值或无法找到更好的平面模型为止。

RANSAC算法的思路是通过反复随机采样,快速求解一个初始的数学模型(如特定平面),并估算该模型的误差范围,用以判断哪些点支持该模型。根据支持模型的点,重新计算模型,进一步提高模型的精度和支持度。通过迭代找到最优的模型及特征点集。这种方法的优点是不需要输入点云的噪声参数,可以有效处理包含较大噪声和离群点的数据集[14]。

对于基于RANSAC的平面拟合算法而言,首先在初始点云中随机选择3个点,计算对应的平面方程为ax+by+cz+d=0(a、b、c、d均为方程的参数);随后计算所有点至该平面的距离di;选取阈值dthreshold,若di≤dthreshold,则该点被认为是模型内样本点,否则为模型外样本点;重复以上步骤,选取最佳拟合参数,即内点数量最多的平面模型参数。

1.2 改进的RANSAC算法

本文提出的改进策略是将一种顺序法向量检测机制应用到RANSAC算法中,通过判断点云数据和拟合得到的平面模型之间的法向向量(Normal Vector,NV)是否符合一定的检核条件,从而使改进的RANSAC算法(M-RANSAC算法)能够自动判断该数据点能否加入平面模型进行迭代计算,进而保证不会使错误的平面模型拥有最多的点云数据,提高所得到平面模型的正确率。

改进的RANSAC算法流程图如图1所示。

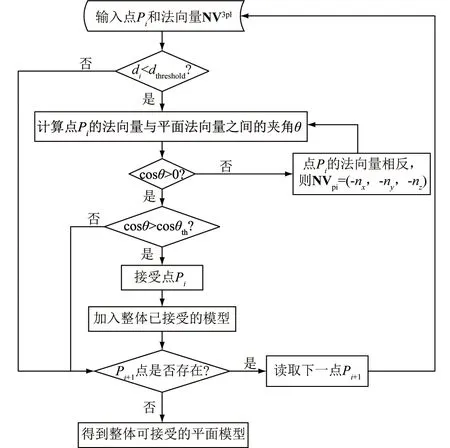
图1 改进的RANSAC算法流程

M-RANSAC算法的具体改进策略如下：设定检核条件的角度阈值θth,在进行迭代计算中,比较每一个点的法向量NV和第一次拟合平面模型时随机选取的3个点的法向量NV3pl之间的夹角θ与阈值θth的大小关系,从而自动判断该点是否可以加入平面模型进行迭代计算,避免了错误的平面模型拥有最多的点云数据情况出现,提高了RANSAC算法得到平面模型的正确率。用M-RANSAC算法比较两个法向量之间的夹角θ与阈值θth之间的关系时,法向量方向必须相同。具体描述如下：

(1)输入每个点参数和第一次拟合平面模型时随机选取的3个点的法向量：Pi=(x,y,z,nx,ny,nz,di)和NV3pl= (nx3pl,ny3pl,nz3pl)。nx、ny、nz分别为法向量的x向、y向、z向分量。

(2)比较每个点与平面之间的距离di与设定的距离阈值dthreshold之间的大小：如dthreshold,则对Pi+1点进行判断和计算。如果cosθ<0,则说明Pi点的法向量存在相反的问题,需要重新定义NVpi=(-nx,-ny,-nz),重新进行夹角θ的判断。

(3)如果cosθ>0,则继续比较θ与角度阈值θth的关系,即当cosθ>cosθth时,则θ<θth,可以接受Pi点,并加入整体已接受的模型;当cosθθth,则不可接受Pi点。

(4)判断Pi+1点是否存在,如存在则转至步骤(1)读取Pi+1点,进行判断;如不存在,则得到整体可接受的平面模型。

2 工程应用

2.1 技术路线

为了验证本文改进的RANSAC算法的可行性和有效性,选取珠江三角洲水资源配置工程输水线路安全监测01—02标段沿线地表房屋建筑的现状测量,计算各处房屋立面倾斜率,掌握其安全状态。本次共扫描测量房屋70座,提取房屋立面301个。

针对长距离引调水工程沿线建筑物跨度大、聚集性强等特点,本文基于三维激光扫描技术的建筑物现状测量主要包括三维激光扫描点云数据准备、单体建筑物提取、建筑物线面拟合、建筑物变形分析4个步骤,技术路线如图2所示。

图2 技术路线

2.2 试验结果

2.2.1 单体建筑物提取

采用基于布料模拟的地面点滤波算法[15],对获取点云进行地面点云滤除;滤除地面点可打断各个地物在地面上的连通性,有利于随后的单体建筑物提取,同时也可大大降低后续数据处理的数据量;完成地面点滤波后,对非地面点云进行连通成分分割,得到各个相互分离的点云子集C1、C2、…、Cn,该点云子集中既包含了单体建筑物点云,也包含了植被、行人、车辆等其他地物;因此需要从点云子集中自动滤除非目标地物,提取出建筑物点云子集B1、B2、....、Bn,获得多个单体建筑物点云;单体建筑物自动提取算法如下：

设点云P进行连通成分分割后的点云子集为Ci(i=1,2,…,n),对各个点云子集进行平均曲率提取,即

(1)

式中：MCi为点云子集Ci的平均曲率;LCj为点云子集Ci中某一点Qj在一定邻域范围内的局部曲率;m为点云子集Ci中的点数。

局部曲率LCj为

(2)

式中λjk(k=0,1,2)为点Qj及其一定邻域范围内的所有点{Q}组成的协方差矩阵COV的三个特征值,且由大到小排列,即λj0≥λj1≥λj2。

COV3×3为

(3)

在获取各个点云子集的平均曲率MC之后,则根据MC的值设定阈值,若某一点云子集的MC小于某一阈值,则该点云子集被判定为建筑物点云Bi(i=1,2,…,n)。图3为单体建筑物分割效果图。

图3 单体建筑物点云分割提取效果

2.2.2 建筑物线面拟合

针对获得的单体建筑物点云数据,利用本文提出的改进随机抽样一致性算法(M-RANSAC)进行平面和边缘探测,将建筑物点云拟合为几何体。采用本文提出的M-RANSAC算法进行平面拟合,可以成功提取每个子集内的所有平面。在现有的角度和距离阈值条件下,当被拒绝在平面外的点集中,无法再拟合提取出一个新的平面,整个迭代过程将会终止。该算法可使提取的平面更加符合建筑物的主要结构特征,大大减少后续的人工处理工作量。最后,可利用提取的建筑物主平面,计算出建筑物的主要边缘线,如图4所示。

图4 建筑物线面拟合结果示意图

2.2.3 建筑变形分析

在上一步骤模型拟合的基础上,取得各个几何模型的定量参数,如垂直倾角、水平倾角、倾斜方向、表面平整度、挠度等。将取得的几何参数与设计参数或多期拟合参数进行对比,分析建筑物几何参数的变形量。

本次珠江三角洲水资源配置工程安全监测01—02标段利用三维激光扫描仪共扫描房屋70栋,提取了301个房屋立面的倾斜率。经统计分析,累积38.87%的房屋立面倾斜率<1‰,累积73.75%的房屋立面倾斜率未超报警值3.5‰,累积83.38%的房屋立面倾斜率未超控制值5‰。其中,29个房屋立面倾斜率在3.5‰～5‰之间,50个房屋立面超出控制值5‰,详细数据见表1。

表1 房屋立面倾斜率数据统计结果

数据表明,有5处房屋(共计79个立面)的立面平均倾斜率超出报警值3.5‰,其平均倾斜率分别为9.58‰、7.83‰、5.61‰、3.73‰、4.15‰。倾斜率超限的立面大多属于砖混结构一层平房或临时搭建的铁皮房,超限原因主要是由于该类房屋建造标准不高。例如,超限立面最多,超出控制值最大的两处房屋如图5所示,图5中红色立面为倾斜率>5‰的超限立面,绿色立面为未超限立面。其超限立面主要为临建墙体,围墙墙体、铁皮房或一层平房。

图5 立面倾斜超限情况示意图

2.3 对比分析

为了验证本文采用方法测量结果的准确性,在本次获取的301个房屋立面中,随机选取其中60个立面,利用徕卡TM50全站仪(测角精度0.5″,测距精度0.6 mm+1 ppm,1 ppm表示距离1 km的随机误差为1 mm)进行立面测量。将两种方法计算得到的立面倾斜率进行差值ΔI对比,以此评定本文采用方法的准确性,对比结果见表2。

表2 2种方法计算倾斜率的差值统计结果

从2种方法对比结果来看,本文采用的方法与全站仪测量的立面倾斜率差值都在1.5‰以内,其中95%的差值都在1‰以内,差值最大为1.34‰。说明采用本文的方法进行建筑物立面测量精度与常规全站仪的测量精度相当,同时在野外数据采集时不会受测量视角限制需要反复调整架站点,提高了数据采集效率,得到的建筑物几何信息更加丰富,可以更加直观地进行三维展示。

同时为了验证本文改进的RANSAC算法的有效性,随机选取经过单体建筑物点云分割的15栋房屋点云数据,利用常规RANSAC算法进行线面拟合。选取的15栋房屋结合扫描点云数据进行实际现场调查有78个房屋立面,分别利用改进的RANSAC算法和常规RANSAC算法进行平面拟合,得到的房屋立面错检率和漏检率如表3。