汾河二坝—义棠段液压坝群对河道冲淤变化影响的数值研究

2023-08-29张小雅任春平

长江科学院院报 2023年8期

张小雅,任春平,杨帆

(太原理工大学水利科学与工程学院,太原 030024)

0 引言

在中小河流上修筑液压坝,不仅可以有效改善河流生态,城市河段的景观,进而实现水系重建、河流生态修复,而且可以提高水资源利用效率[1-3]。低水头液压坝结构简单,施工方便,可调控度较高,在中小河流上得到较为广泛的应用。但同时,这些低水头坝也会改变河流水沙过程,特别是在梯级坝群河段,会对河道冲淤特性产生重要影响[4]。

汾河中游生态修复核心段始于汾河二坝,终于文峪河入汾河口,全长82.2 km,共计修筑15座液压坝,相邻坝间距约5 km,每座液压坝由许多能自由升降的面板组成,可实现升坝拦水、塌坝行洪的目的,每个面板长6 m,高3～5 m,一般可将每座液压坝分成主槽坝和边滩坝,遇到大洪水时可全部塌坝泄洪,小洪水时可以根据需要调整坝的开启。图1给出了汾河中游某一座液压坝不同运行方式过流场景(图1(a)—图1(c))及液压坝下游主槽摆动对堤防护坡的侵蚀(图1(d))。由图1可见,通过调控液压坝(主槽段、边滩段)不同运行状态,可在一定程度上实现对水流过流状态的调控,但不同运行状态对河道冲淤特性有怎样的调控影响,还有待进一步深入研究。

图1 液压坝不同运行情况过流场景及液压坝下游主槽摆动对堤防护坡的侵蚀

目前,已有的研究大多关注高水头坝对河道冲淤特性的影响,关于可调控低水头梯级坝群的研究还鲜有报道。河道中修筑挡水建筑物后,会改变水动力条件,进而影响泥沙的输移[5],对该方面的研究多采用二维数值模拟方法[6-9],数值模型涉及水动力过程[10-13]和泥沙输移过程[14-18]。已有学者就汾河中游梯级液压坝群对洪水演进及床面形态影响进行了初步研究。任春平等[19]基于Delft3D数值研究了汾河中游梯级液压坝群不同运行方案对洪水演进的影响。Ni等[20]基于二维水动力-泥沙-床面形态耦合模型研究了不同运行方案下的床面形态演变,但仅仅考虑了黏性沙。针对上述问题,本文以汾河中游二坝到义棠段为研究河段,该河段包含15座梯级液压坝,基于Delft3D FM软件构建二维水沙数学模型,同时考虑黏性沙和非黏性沙,研究在不同洪水频率下,液压坝群不同运行方案对河道冲淤变化的影响。本研究将为汾河中游液压坝群的运行提供科学依据,进而为该段河流生态修复的成功实施奠定基础。

1 Delft3D FM模型构建及验证

本文采用1996年、2016年、1995年和1998年洪水过程下二坝和义棠水文站观测所得水沙数据,基于Delft3D FM软件构建二维水动力-泥沙耦合数学模型,对汾河二坝—义棠段的水沙输移过程进行数值模拟及验证。

1.1 控制方程

Delft3D FM软件包括水动力、波浪、泥沙和水质等模块,可应用于海岸、河口和河流等区域的工程研究。本文通过将D-FLOW和D-MOR模块耦合构建二维水沙数学模型[21]。

模型采用σ坐标系,二维水动力模型控制方程如下。

(1)连续方程为

(1)

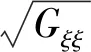
ξ方向和η方向的动量方程分别为：

(2)

(3)

式中：w为垂向流速;σ为比例垂直坐标;ρ0为水的密度;Pξ和Pη分别为ξ和η方向上的静水压力梯度;Fξ和Fη分别为ξ和η方向上由水平雷诺应力引起的不平衡;Mξ和Mη分别为ξ和η方向上由外部导致的动量;νV为垂直涡黏系数。

(2)泥沙输移方程。黏性沙输沙率的计算采用Partheniades-Krone公式,即：

(4)

(5)

(6)

式中：E和D分别为侵蚀通量和沉积通量;M为侵蚀系数(kg/m2/s);ρs为泥沙密度(kg/m3);τ为床面剪切应力;τcr,e和τcr,d分别为临界侵蚀和临界沉积床面剪切应力(Pa);ωs为泥沙沉降速度(m/s);c为含沙量;cb为接近底部计算层的平均泥沙浓度(kg/m3);Δzb为近底层泥沙厚度(m)。

非黏性沙输沙率的计算采用Engelund-Hansen (1967)全沙公式,即

(7)

式中：Sb和Ss,eq分别为推移质和悬移质输沙率;α为校准系数;q为流速;Δ为相对密度,Δ=(ρs-ρ0)/ρ0,ρs为泥沙密度(kg/m3);C为谢才系数;D50为泥沙中值粒径(mm);g为重力加速度。

泥沙输运基本方程为

(8)

床面高程变化方程为

(9)

式中：c为含沙量;εs,x和εs,y分别为x、y方向的泥沙扩散系数;zb为床面高程;Sx、Sy分别为x、y方向的输沙分量。

1.2 模型网格划分

模型计算域为汾河二坝—义棠段,全长82.2 km,河宽100～400 m,平均纵向坡度为0.03%,本文考虑二坝—义棠段间汇入的昌源河、龙凤河、磁窑河和文峪河4条支流,沿程共设15座液压坝,见图2。

图2 研究区域及15座液压坝平面位置

图3 计算网格

对研究区域进行非结构化三角形网格划分,划分网格尺寸为50 m,对河宽较窄处进行局部加密,网格数量为18 855个,网格节点的夹角余弦值<0.02,满足正交性要求,见图3。

1.3 边界条件及参数设置

本文将二坝作为上游边界,义棠作为下游边界。对于水动力场,上游设为流量-时间序列,下游设为水位-时间序列,支流边界采用流量-时间序列。对于泥沙冲淤过程,上下游均设为含沙量-时间序列。其中1996年和2016年洪水重现期分别为10、2 a一遇。1995年和1998年洪水过程为常发洪水,1996年二坝和义棠2个断面含沙量较大,1998年断面含沙量介于1995年和1996年之间,2016年由于汾河二库的运行,断面含沙量极小,见图4。

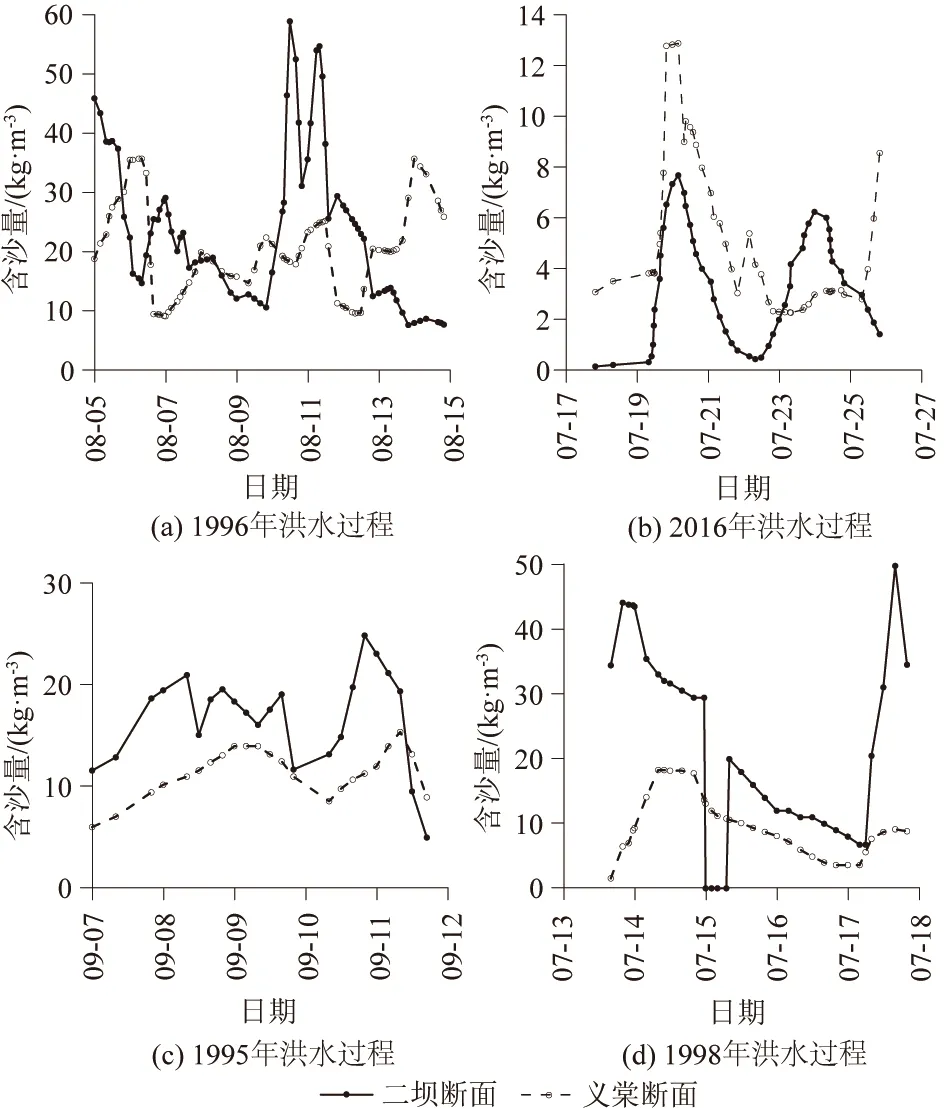
图4 二坝、义棠断面含沙量

本文在数值模拟过程中涉及泥沙、河道糙率及模拟时间步长相关参数,下文给出具体参数设置。模拟河段主要由细沙和轻沙壤土组成,来洪量较大的情况下,泥沙以推移质和悬移质形式运动,因此采用黏性沙和非黏性沙的泥沙组分[22-23],具体参数见表1。

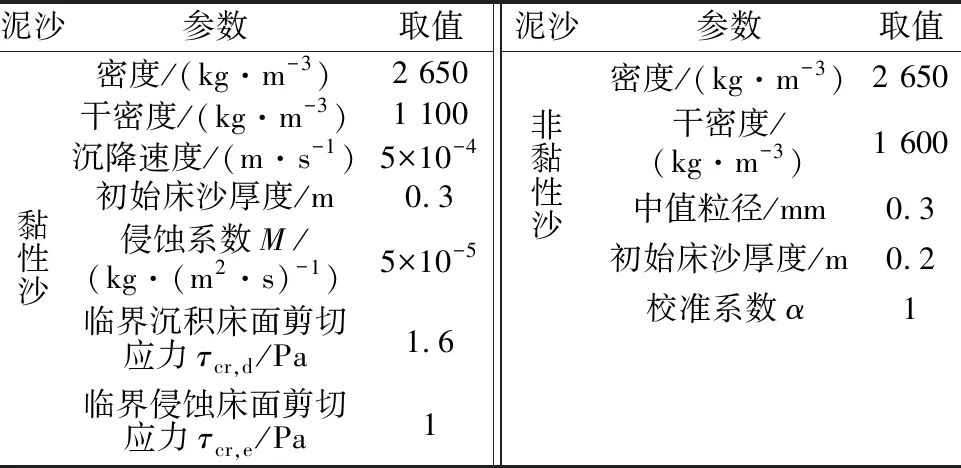
表1 泥沙模型参数

以上下游水位和流量过程实测资料为基础,率定主槽糙率为0.007,边滩糙率为0.03。D-FLOW模块使用显式平流计算原理,根据CFL(Courant-Friedrichs-Levy)计算准则自动设置动态时间步长限制,每个时间步长的最大库朗数(Max Courant nr)设为0.7[21]。

1.4 模型验证

本文采用1996年和2016年洪水过程进行水动力模型验证,验证结果见图5。由图5可知,二坝断面水位和义棠断面流量的峰值和位置都与实测数据较为吻合。由于未考虑植被对局部糙率的影响,部分时段水位、流量的模拟结果与实测数据有差异。总体来看,整个洪水过程的水位和流量的计算结果与实测数据吻合较好,说明构建的二维水动力模型精度较高,可以用于后续水沙输移模拟。

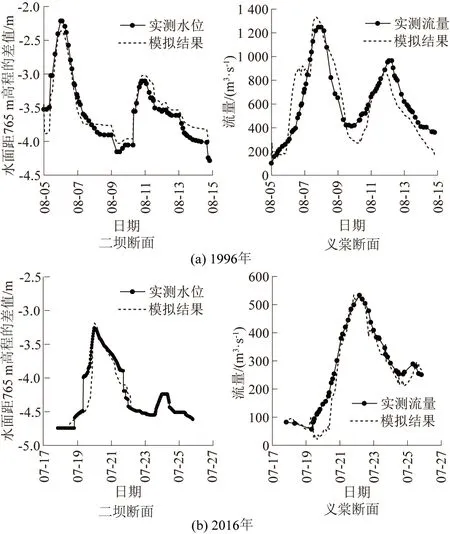
图5 1996年和2016年洪水验证结果

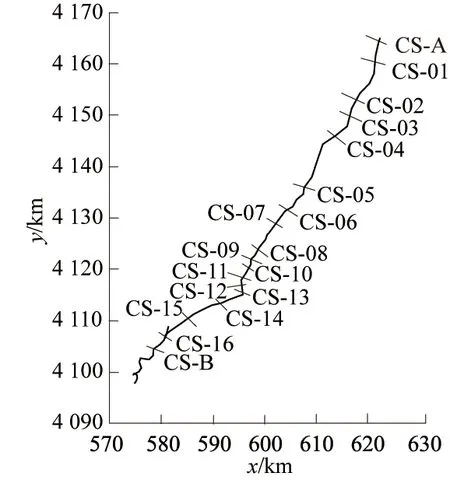
图6 验证断面位置

本文采用断面含沙量和断面形态进行泥沙模型验证,各断面位置见图6,二坝—义棠方向(右上—左下)共18个断面,依次为CS-A、CS-01—CS-16、CS-B。将2016年洪水过程下二坝下游断面CS-A和义棠上游断面CS-B含沙量的计算结果与实测数据进行对比,如图7所示。将2014年洪水过程下河道16个断面形态变化的计算结果与实测数据进行对比,因篇幅有限仅展示部分断面的验证图,见图8。

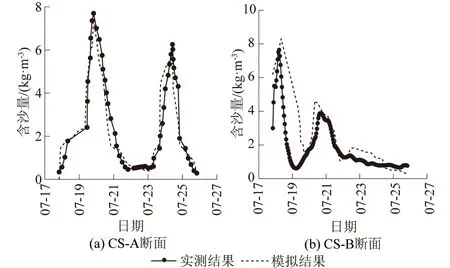
图7 断面含沙量实测与模拟结果比较

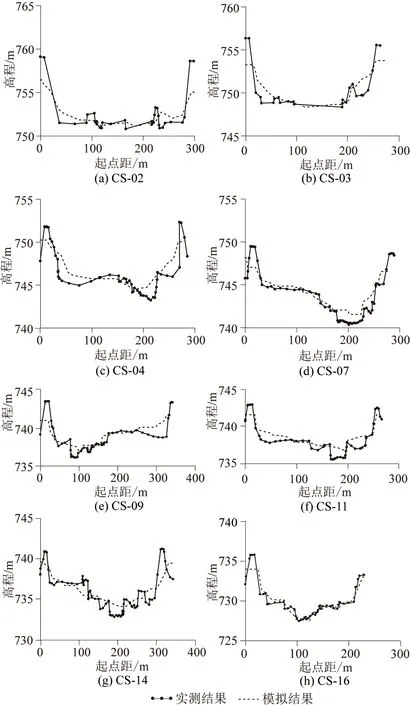
图8 断面形态实测结果与模拟结果比较

根据统计学方法[24]对模拟结果进行评价,计算公式为

(10)

计算得出,断面含沙量的模型效率系数分别为0.87和0.63,评价结果为极好和较好,断面形态的模型效率系数为0.45～0.73,评价结果为好至较好。由于未考虑植被对局部糙率的影响,部分时间段的断面含沙量模拟结果与实测数据有差异。软件对地形数据的差值处理导致断面形态较为均匀,部分位置的模拟结果与实测数据有差异。总体来看,本文所构建的二维水沙数学模型模拟精度较高,能够较好地模拟出河道床面形态变化过程,可以用于液压坝群对河道冲淤变化影响的数值研究。

1.5 液压坝工况设置

本文研究的河段在15个断面处筑有液压坝,每个断面处液压坝可分为主槽坝和边滩坝。为研究液压坝群不同运行方案对河道冲淤变化的影响规律,本文针对4种运行方案进行了研究,见表2。

表2 液压坝运行方案

2 液压坝群对河道冲淤变化的影响

本节运用上述二维水沙数学模型,对4场洪水情况下液压坝群的不同运行方案进行模拟,研究液压坝群对河道冲淤变化的影响。

2.1 水动力场及床面高程变化

本文对14#液压坝进行水动力及床面高程变化分析。表3给出了坝前水深分布,在1996年、2016年、1995年和1998年4场洪水情况下,无液压坝运行时(方案1),坝前水深分别约为1.0～1.4、0.7～1.2、0.6～1.1、0.5～0.8 m,坝后局部流速最大约为2.5、2.0、2.0、1.5 m/s。液压坝全部运行时(方案2)对水流起到拦蓄作用,坝前水深分别增加了约0.8～1.4、0.5～1.1、0.9～1.0、0.8～1.0 m,形成过坝溢流,坝后局部流速最大约为6.0、3.0、4.0、2.0 m/s,为无坝运行时的1.3～2.4倍。仅有主槽坝运行时(方案3),坝前水深分别增加了约0.3～0.4、0.1～0.2、0.2～0.4、0.1～0.2 m,坝后局部流速最大约为3.0、2.5、2.5、2.0 m/s,为无坝运行时的1.2～1.3倍。仅有边滩坝运行时(方案4),14#坝的坝前水深分别增加了约0.1～0.2、0～0.1、0～0.1、0～0.1 m,水流流向主槽,边滩坝后流速明显减小,约为0.1～0.2 m/s,主槽流速与无坝运行时相近。

表3 14#坝的坝前水深、坝后流速分布

表4 15座液压坝前床面高程变化ΔZ

在1996年、2016年、1995年和1998年4场洪水情况下,由于液压坝拦水拦沙的作用,坝前产生泥沙淤积,坝后局部流速较大,坝后形成床面冲刷(坝上下游各100 m处)。无液压坝运行时,泥沙冲淤范围约为-0.5～0.5、-0.5～0.25、-0.4～0.2、-0.4～0.2 m。液压坝全部运行时,由于液压坝群联合作用,处于下游的14#坝前泥沙淤积厚度较小,泥沙冲淤范围约为-0.5～0.6、-0.5～0.05,-0.5～0.1、-0.5～0.2 m。仅有主槽坝运行时,冲淤范围约为-0.5～0.5、-0.5～0.2、-0.5～0.1、-0.5～0.2 m。仅有边滩坝运行时,坝后由于流速较小,边滩处产生淤积最大值约为0.5、0.3、0.15、0.2 m,主槽冲淤范围与无坝运行时相同。

2.2 15座坝液压坝前泥沙冲淤变化

本节选取每座液压坝上游100 m处的断面作为参考,分析不同液压坝运行方案下15座液压坝前的床面泥沙冲淤高程变化范围(见表4),研究液压坝群对河道冲淤变化的影响规律。

由表4可知,在1996年、1995年、1998年3场洪水过程下,相对于方案1(无液压坝运行)泥沙冲淤变化情况,方案2(液压坝全部运行)时1#—9#坝前泥沙淤积厚度增加0.05～1.07 m,冲刷范围减小0.04～0.40 m,而10#—15#液压坝处在河道下游,流速和含沙量相对减小,泥沙冲淤范围减小0.05～0.60 m;方案3(仅有主槽坝运行)中坝前泥沙淤积无明显变化规律,冲刷范围相对增加0.05～0.30 m;方案4(仅有边滩坝运行)中泥沙冲淤变化范围与方案1近似。2016年洪水过程由于含沙量较小,液压坝全部运行时,1#—3#坝前淤积厚度增加0.05～0.10 m,仅有主槽坝运行时床面整体冲刷范围增加0.1～0.4 m,仅有边滩坝运行时整体泥沙冲淤范围与方案1相近。

2.3 冲淤总量分析

下面分析4场洪水情况下整个模拟河段内总的泥沙淤积量,公式为[22]

ΔV=V二坝-V义棠。

(11)

图9 4场洪水过程在不同运行方案下的泥沙淤积

式中：ΔV为河道淤积总量;V二坝为二坝断面入口泥沙量(万m3);V义棠为义棠断面出口泥沙量(万m3)。

图9给出了4场洪水情况下的泥沙淤积总量,可知河道中泥沙总体呈现淤积状态。1996年洪水过程下,方案1河道泥沙淤积量约为242.3万m3,与无坝运行时相比,方案2—方案4泥沙淤积量分别多了约81.2万、10.2万、3.1万m3。2016年洪水过程下,由于汾河二库的运行,河道内含沙量较小,方案1河道泥沙淤积量约为4.9万m3,与无坝运行时相比,方案2—方案4分别多了约0.4万、0.1万、0.05万m3。1995年洪水过程下,方案1河道泥沙淤积量约为62.3万m3,与无坝运行时相比,方案2—方案4分别多了约5.3万、3.1万、1.3万m3。1998年洪水过程下,方案1河道淤积量约为22.1万m3,与无坝运行时相比,方案2—方案4分别多了约8.1万、3.3万、1.5万m3。可知在4场洪水过程下,方案2(液压坝全部运行)泥沙淤积量最大,约为方案1的1.08～1.36倍,方案1(无液压坝运行)淤积量最小,方案3和方案4(仅有主槽坝运行和仅有边滩坝运行)的淤积量值介于两者之间,分别约为方案1的1.04～1.15倍、1.02～1.07倍。