基于小波的SSA-ELM大坝变形时空预测模型
2023-08-29宋宝钢包腾飞向镇洋王瑞婕
宋宝钢,包腾飞,3,向镇洋,王瑞婕
(1.河海大学 水文水资源与水利工程科学国家重点实验室,南京 210098;2.河海大学 水利水电学院,南京 210098;3.三峡大学 水利与环境学院,湖北 宜昌 443002)
0 引 言
截止2020年我国已建成各类水库98 566座,水库总库容9 306亿m3[1]。混凝土坝在长期运行过程中,发挥了巨大的工程效益,同时也存在一定的风险,特别是一旦溃决失事,不仅大坝损毁,还会给下游带来严重灾害[2]。变形作为混凝土坝监测的重要物理量,能直观地反映混凝土坝的安全性态。因此开展混凝土坝的变形监测并根据监测数据建立混凝土坝的预测预报模型,对保障混凝土坝的安全具有重要意义。
传统的大坝变形预测预报模型主要包括统计模型、确定性模型和混合模型[3]。该类数学模型将环境量作为自变量,效应量作为因变量,利用统计回归方法建立效应量与环境量之间的函数关系,并对模型中的各分量进行物理解释,进而分析大坝的工作性态[4]。随着计算机技术和人工智能的发展,机器学习算法在大坝变形的预测中得到了广泛的应用。钱秋培等[5]研究了支持向量机和粒子群算法在混凝土坝变形监控模型中的应用;曹恩华等[6]提出了一种基于变量筛选优化极限学习机的混凝土坝变形预测模型;李涧鸣等[7]提出了一种基于小波理论的EGM-ISFLA-SVR 的大坝变形组合预测模型,分别应用均值GM(1,1)模型和基于改进的混合蛙跳算法的支持回归机模型对变形序列的趋势项和周期项进行建模和预测;Li等[8]研究了STL-extra-trees-LSTM组合模型在大坝水平位移预测中的应用;Shu[9]基于时间注意和变分自动编码器的长短期记忆网络框架,对大坝的位移进行了预测。
上述模型对保证大坝安全发挥了一定的作用,但均为为单测点模型。该模型没有考虑各个测点间的相互关系,无法从整体上对分析对象进行评价,对于大坝上没有布置测点的位置难以发现其变形规律。若对每个测点单独建立模型,势必造成模型众多、分析工作量巨大。为此,一些学者对大坝变形的多测点模型进行了研究。黄铭等[10]综合了大坝多个测点的位移向量建立多测点位移向量统计模型;李端有等[11]采用有限元法计算水压分量和温度分量,建立了混凝土拱坝多测点确定性模型;王建等[12]利用多测点混合模型对混凝土坝受冻区坝体弹性模量进行了反演;王继敏等[13]基于面板数据建立了锦屏一级拱坝的位移时空模型,对大坝变形性态进行了分析。
总体来看,这些模型能够在一定程度上挖掘出大坝变形的时空信息,但大多为基于统计回归的多测点模型,其主要存在以下问题:① 由于大坝是一个复杂的系统,其环境量和效应量之间具有复杂的非线性映射关系,而基于统计回归的多测点模型无法反映这种关系;② 引入测点坐标变量的多测点模型往往因子众多,采用统计回归分析时,自变量间存在多重共线性问题,且容易导致方程出现病态问题;③ 受复杂条件的影响,大坝位移测值难免存在高频噪声,势必对模型分析的准确性造成影响。这些缺点直接制约了模型的预测预报精度。为解决上述问题,建立更高精度的大坝变形时空预测模型,提出了一种考虑空间测点位置坐标、基于小波的SSA-ELM大坝变形时空预测模型,并以某混凝土坝为例,验证了模型的可行性和准确性。
1 混凝土坝变形时空分布模型
根据现有大坝安全监测理论[3],在水压力、扬压力和温度等荷载作用下,大坝任一点的位移δ可表示为水压分量δH(t)、温度分量δT(t)和时效分量δθ(t)三部分之和,具体可按下式表示,即
式中:H为坝前水深;t为监测日至始测日的累计天数;θ=t/100;ai为水压分量回归系数;b1i、b2i均为温度分量回归系数;c1、c2均为时效分量的回归系数;a0为常数;H0、t0、θ0均为初始值。
式(1)为混凝土坝变形的单测点模型,该模型仅从时间维度描述了混凝土坝的变形规律,难以刻画其空间变形规律。而混凝土坝的变形观测序列是一种同时具有时间和空间属性的二维时空数据结构。时空分布模型与单测点模型相比,由于考虑了测点间的相互位置关系,因此,能够从整体上把握大坝的变形规律,及早发现因局部因素而使某些部位(x,y,z)偏离真实位移场的情况,从而及时分析原因、消除隐患。同时,时空分布模型融合了多个测点的数据,能够对训练集样本进行扩充,从而挖掘出更多的变形时空特性,进而提高模型的预测精度。
考虑空间上的多个测点,并引入测点的空间坐标变量(x,y,z),混凝土坝变形时空分布模型可概化为
δ=f1[f(H),f(x,y,z)]+f2[f(T),f(x,y,z)]+
f3[f(θ),f(x,y,z)] 。
(2)
式中f1、f2、f3分别为与水压、温度、时效有关的函数。
联立式(1),并将各项按多元幂级数展开同时略去高次项得到混凝土坝变形时空分布模型
(3)
式中Aklmn、Bjklmn、Cjklmn为回归系数。
当研究梁的挠曲线时,上述模型退化为
(4)
2 基于小波的SSA-ELM大坝变形时空预测模型构建
大坝变形的时空模型中,不仅包含了单测点模型中的各项因子,还包含了坐标变量及坐标变量与水压、温度和时效因子的组合变量,其模型自变量众多,以式(4)中梁的挠曲线时空模型为例,其变量数就多达43个,若采用回归分析建模则极易使得方程出现病态问题。同时,基于统计回归的时空分布模型难以刻画环境量与效应量之间复杂的非线性关系,且自变量间存在多重共线性等问题。受复杂环境的影响,大坝原始观测数据中难免会存在一些噪声。这些问题对建模造成了很大的影响,制约了模型的预测精度。考虑到麻雀搜索算法(Sparrow Search Algorithm,SSA)和极限学习机(Extreme Learning Machines,ELM)的优点,本文首先采用小波算法去除观测数据中的噪声,接着利用非线性处理能力强、具有良好泛化能力的SSA-ELM模型建立大坝变形时空模型,对各测点未来的变形进行预测,同时,利用该模型对某一未设置观测点部位的变形进行了预测。
2.1 大坝变形监测数据的小波去噪方法
大坝变形监测数据可看作一种信号,受复杂环境的影响其通常会受到噪声的污染,其中的噪声主要是由随机因素及观测误差产生的。为了从信号中提取出表征被检测对象特征的有用信息,提高数据精度,有必要对信号进行去噪处理[14]。小波分析 (Wavelet Analysis)是一种时间-频率分析信号的方法,是在20世纪80年代后期从信号领域逐步发展起来的,与傅里叶变换的单分辨率相比,其拥有多分辨率分析的特征,是一种很好的信号去噪分析方法。包含噪声的大坝变形观测信号s(n)可表示为
s(n)=f(n)+σe(n) 。
(5)
式中:s(n)为含有噪声的信号;f(n)为有用信号;e(n)为白噪声信号;σ为系数。

2.2 大坝变形序列的ELM模型
传统的大坝位移预测模型无法反应大坝变形随机性及高度非线性的特点,其预测结果往往无法满足精度要求。ELM是一种针对单隐含层前馈神经网络的新算法。相对于传统前馈神经网络训练速度慢,容易陷入局部极小值点,学习率的选择敏感等缺点,ELM算法随机产生输入层与隐含层的连接权值及隐含层神经元的阈值,且在训练过程中无需调整,只需要设置隐含层神经元的个数,便可以获得唯一的最优解。与传统训练方法相比,ELM方法具有学习速度快,泛化性能好等优点[16],能够显著地提高大坝变形的预测精度。ELM基本网络结构如图1所示。
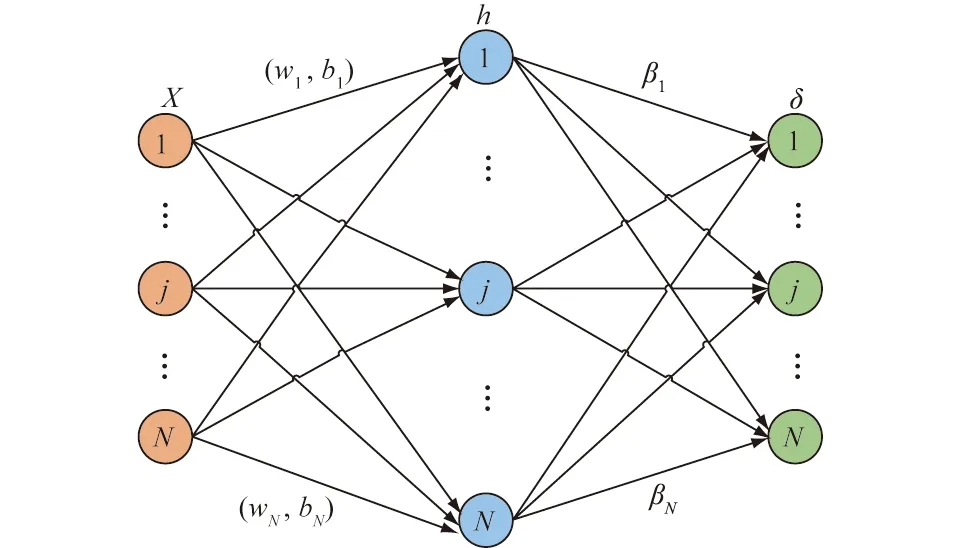
图1 ELM基本网络结构
假设有N个样本(Xi,δi),其中δi表示去噪后的变形测值,Xi=[xi1,xi2,…,xin]T表示大坝变形时空模型中的环境量,xi1,xi2,…,xin表示水压、温度、时效和坐标变量因子及其组合形式。则大坝变形时空预测模型的输出oj可表示为
式中:L为隐层节点数;g()为激活函数;Wi为输入层与隐含层的连接权值;bi为第i个隐层单元的阈值;βi为输出权值。
极限学习机在随机确定权重Wi和阈值bi后,通过优化输出权重βi,从而使网络输出oj与目标值δi之间的误差达到最小。
2.3 ELM网络的优化
在ELM网络中,输入层权值和隐含层阈值通过随机生成,这种方法在一定程度上提升了模型的鲁棒性和学习速度,然而输入层权值和隐含层阈值的随机性容易造成网络不稳定进而对模型预测精度造成影响[17]。因此,有必要采用优化算法对ELM的输入层权值和隐含层阈值进行优化以增强其预测性能。
SSA是Xue等[18]根据麻雀觅食并逃避捕食者的行为而提出的一种新型智能优化算法。文献[19]的试验分析表明与目前广泛使用的灰狼优化算法(Grey Wolf Optimizer,GWO)、粒子群优化算法(Particle Swarm Optimization,PSO)和引力搜索算法(Gravitational Search Algorithm,GSA)相比,麻雀搜索算法具有更强的全局搜索能力并且收敛速度更快。为此,本文选用麻雀搜索算法对极限学习机的输入层权值和隐含层阈值进行优化。在SSA中,每只麻雀位置对应其中的一个解。麻雀在觅食过程中有3种行为:①作为发现者寻找食物;②作为加入者跟随发现者觅食;③作为警戒者决定种群是否继续觅食。其中,发现者和加入者两者的身份是动态变化的,可相互转换,但两者比例保持恒定。发现者作为种群觅食的引导者,拥有更高的适应度值,可以获得更加广阔的搜索区域。而加入者为获取更高的适应度值跟随发现者进行觅食,同时一些加入者可能会不断地监控发现者并夺取食物资源来提高自身的捕食率。种群会随机选取一部分麻雀作为警戒者进行监视和预警,这些麻雀大概占整个种群的10%~20%,当种群边缘的麻雀在觅食过程中察觉到危险时,会迅速提醒整个种群做出反捕食行为[19-20]。SSA算法的更新公式如下所述。
发现者的位置更新公式为
式中:t为当前迭代次数,j=1,2,3,… ,d(d为维数);itermax为最大迭代次数;Xi,j为第i个麻雀在第j维中的位置信息;α∈(0,1]为随机数;R2∈[0,1]为预警值;ST∈[0.5,1],为安全值;Q为服从正态分布的随机数;L为元素全为1的d维行向量。
当R2 加入者的位置更新公式为 式中:XP为当前探索者的最优位置;Xw为当前全局最差位置;A为d维行向量,其中每个元素随机赋值为 1 或-1,A+=AT(AAT)-1;当i>n/2时,表明适应度最低的第i个加入者没有获得食物,此时需要前往其他地方觅食。 假设意识到危险的麻雀占总数的10%~20%,随机产生这些麻雀最初的位置,则建立全局最优位置公式为 式中:Xb为当前全局最优位置;β为步长控制因子,服从均值为 0,方差为 1 的正态分布的随机数;k为随机数,且k∈[-1,1];fi为当前麻雀个体的适应度值;fg为当前全局最佳适应度值;fw为当前全局最差适应度值;λ为一很小的常数,避免分母为0。 综上,本文在大坝变形时空分布模型的及小波分析的基础上,采用SSA-ELM建立了环境量与大坝变形值之间的非线性映射关系,进而构建了基于小波的SSA-ELM大坝变形时空预测模型。首先采用小波算法去除大坝原始观测数据中的噪声,接着以大坝变形时空分布模型中的各因子作为ELM的输入,去噪后的位移值作为输出,以训练集的均方误差(MSE)作为SSA算法的适应度值,用SSA算法寻求ELM的最优输入权值和阈值,最后用训练好的模型对测试集进行预测。算法流程如图2所示。 图2 算法流程 图3 径向位移测点布置 以位于雅砻江下游的某混凝土双曲拱坝为例,选取位于9号坝段的5个径向位移测点进行研究(如图3所示)。假定PL9-2测点未设置观测点其径向位移未知,利用其余4个测点建立基于小波的SSA-ELM大坝变形时空预测模型,采用该模型对建模的4个测点及PL9-2测点未来一段时间的位移做预测。 图中各测点的高程如表1所示。考虑到该拱坝厚度较薄,顺河向的y坐标相比于竖直向的z坐标变化较小,因此,考虑z方向的坐标变化对拱坝径向位移的影响,建立该拱坝径向位移的时空预测模型,其表达式可表示为式(8)。 所选坝段从坝顶到坝基布置有5个正垂线测点PL9-1、PL9-1、PL9-3、PL9-4和 PL9-5,和一个坝基倒垂线测点IP9-1,测值为每日一测。对2013年10月2日—2018年12月31日该坝段正垂线测点的径向位移数据进行去噪处理。采用Matlab程序进行建模和计算。根据前述小波去噪理论,经反复尝试后选用sym6小波对5个测点实测径向位移进行6层分解,采用自适应阈值进行软阈值去噪,去噪结果如图4所示。 表1 各测点高程 图4 小波去噪结果 将各测点去噪后数据划分为训练集和测试集,其中2013年10月2日—2018年9月18日共1157组数据作为训练集,2018年9月19日—2018年12月31日的100组数据作为测试集。 为了消除不同物理量由于量纲不同而对模型造成影响,在建模之前先将不同物理量归一化到[0,1],即 (10) 式中:y′为某一物理量归一化后的值;y为某一物理量归一化之前的值;ymin为某一物理量最小值;ymax为某一物理量最大值。 图5 SSA-ELM适应度曲线 图6 模型预测结果 为了验证所提模型的可行性,分别建立了基于ELM的时空分布模型和基于统计模型的时空分布模型并与所提模型进行对比。为了克服偶然性及模型的不稳定性,各模型分别独立运算30次,取30次的平均值作为最终的结果。图5为SSA-ELM模型的收敛过程,由图可知所提模型具有很快的收敛速度和较高的精度,迭代到第5步时训练集的均方误差收敛到了0.002 1。图6给出了各模型的预测结果,结果表明:SSA算法优化的ELM模型预测精度明显高于传统的ELM模型和统计模型,具有很好的泛化能力。由此可见,SSA-ELM模型与统计模型相比,前者能够挖掘出环境量与效应量之间的非线性关系,同时克服了统计模型容易导致方程病态的问题,因而表现出更好的性能。由于常规ELM模型输入权值和阈值是随机生成的,模型容易陷入局部最优且不稳定,通过SSA算法对其输入权值和阈值优化后其性能得到了很大的提升,表明了SSA算法具有很强的全局寻优能力。 采用训练好的模型对未参与模型训练的PL9-2测点位移进行预测,结果如图7所示。由图可知预测值过程线与实测值过程线具有相同的变化趋势,且精度较高,表明所提模型基本能预测出该坝段任一点的径向变形,具有良好的时空预测性能。这主要是因为拱坝是个空间壳体结构,其各测点变形具有一定的协联关系,通过将测点坐标引入自变量中,能够挖局出各测点空间上的变形关系,进而实现对未布置测点部位变形的预测。 图7 PL9-2测点预测结果 为了定量的评价各模型的性能,比较了各模型的复相关系数(R2)、均方根误差(RMSE)和平均绝对误差(MAE)3个指标,如表2所示。 表2 各模型预测性能比较 结果表明所提模型的R2、RMSE和平均绝对误差MAE均显著高于ELM模型和统计模型,其中ELM模型的各项指标均最低,这主要是由于ELM随机的初始权值和阈值对训练的性能有较大影响,同时也表明采用SSA算法优化ELM的权值和阈值使得模型性能得到了显著地提升。 本文提出了一种基于小波的SSA-ELM大坝变形时空预测模型,该模型弥补了现有单测点模型的不足,泛化能力好,预测精度高。主要结论如下: (1)小波算法可以有效地去除原型观测数据中的噪声项,保证了模型分析的准确性和精确度。 (2)采用麻雀搜索算法对极限学习机进行优化后,其预测精度得到了显著的提升。 (3)所提模型在未布置测点的部位能够表现出良好的时空预测性能,对整体把握大坝的变形趋势具有重要作用,有效地弥补了因某个测点损坏而无法获得准确测值的缺陷。 (4)所提模型R2、均方根误RMSE和MAE 3个指标均显著高于ELM模型和统计模型,对大坝及其他相关水工建筑物的变形时空预测具有重要参考价值。2.4 基于小波的SSA-ELM大坝变形时空预测模型构建
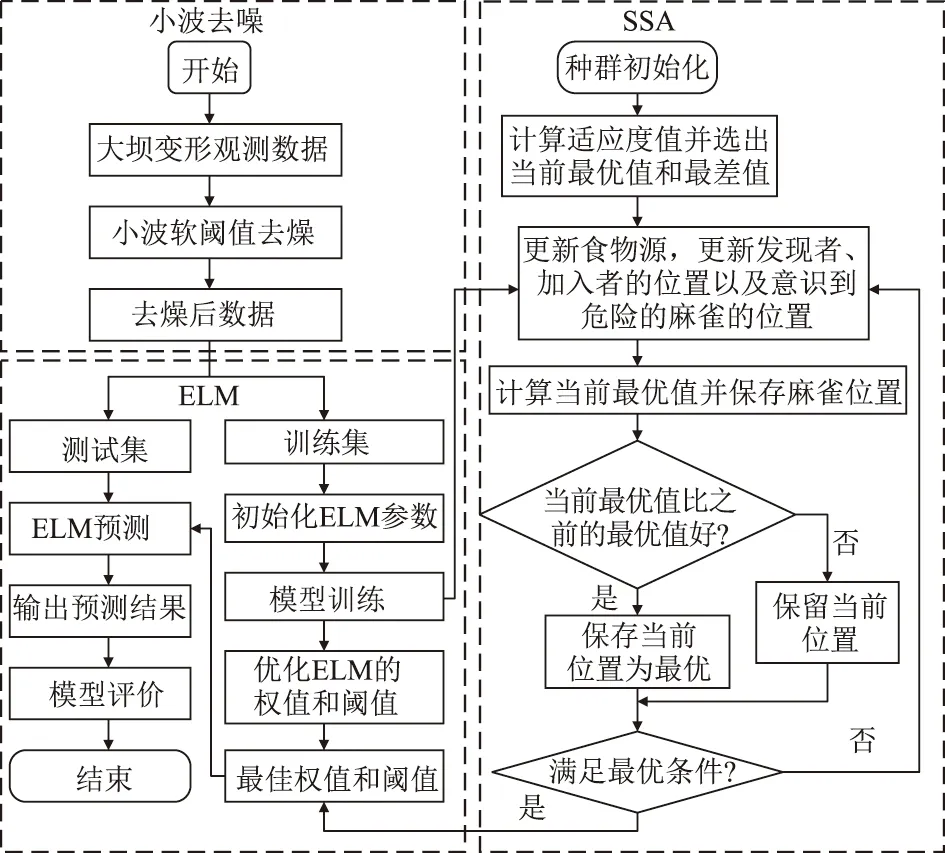
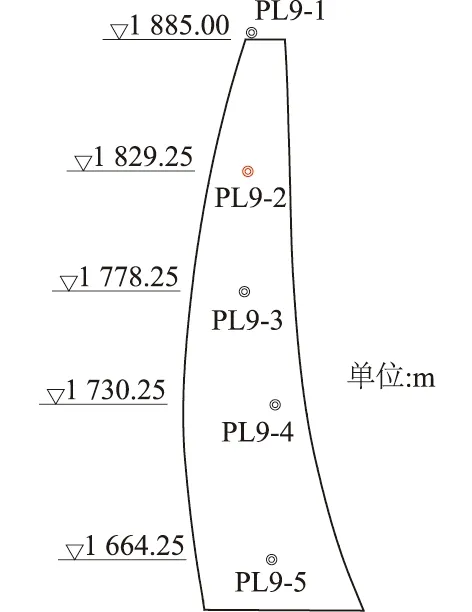
3 实例分析
3.1 数据的获取及预处理

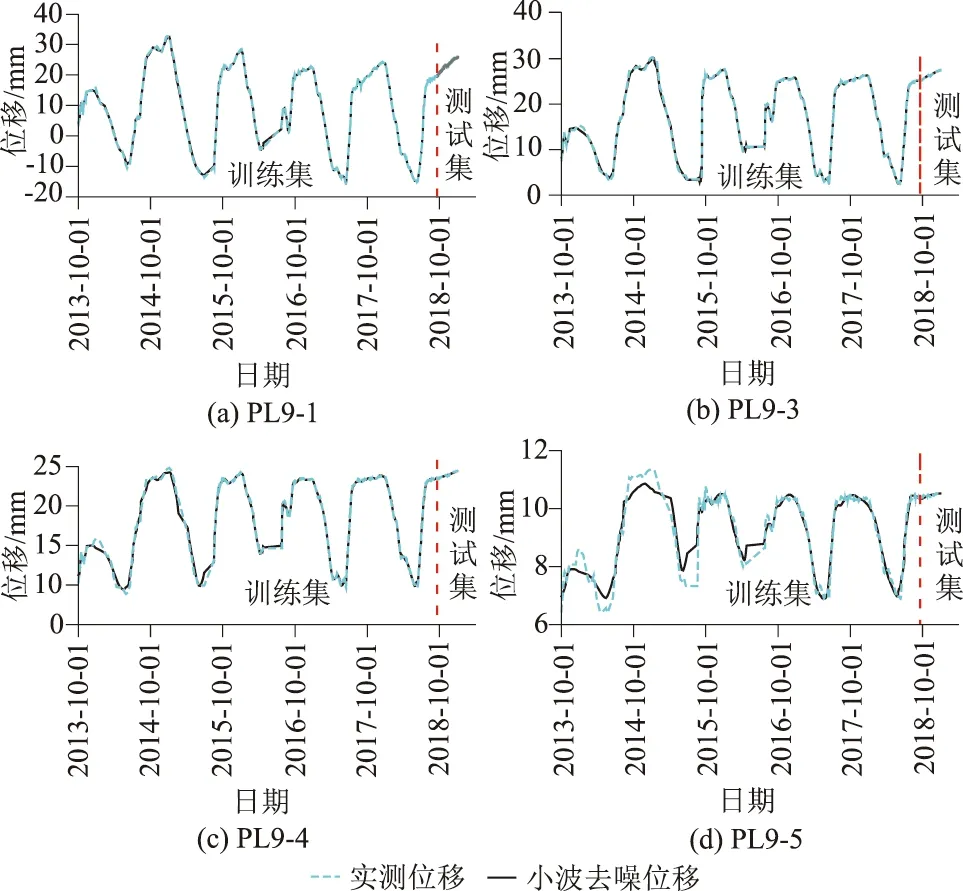
3.2 模型的构建及参数设置
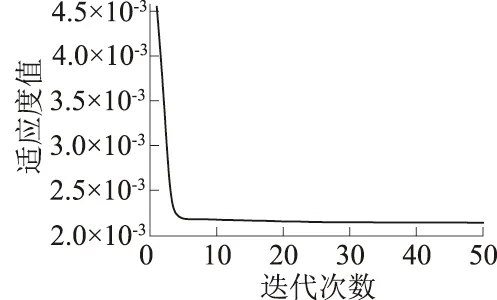
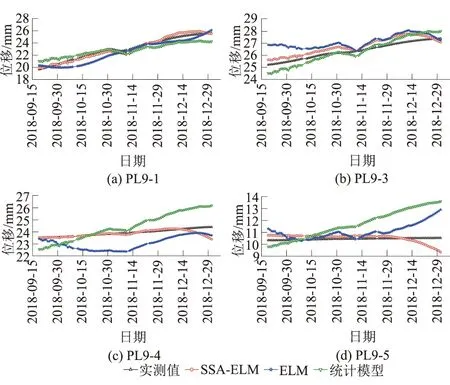
3.3 结果及分析


4 结 论
