肯尼亚某迷宫堰溢洪道水力特性
2023-08-29闫彭彭
闫彭彭
(上海市政工程设计研究总院(集团)有限公司 合肥分公司,合肥 230061)
0 引 言
迷宫堰(Labyrinth Weir)是一种在平面布置上为锯齿形的特殊堰型,虽然针对该堰型的研究始于20世纪20年代,但直至七八十年代该堰型才具有一定的应用规模[1-3]。我国在20世纪80年代后期开始进行相关的应用研究,如:张绍芳等[4]通过多次试验,基于统计原理,对影响迷宫堰水力特性的诸多因素进行简化,提出流量系数计算方法,并对迷宫堰宫宽、堰长、堰高和水头等设计参数给出初步建议;王仕筠等[5]分析了迷宫堰经验计算曲线,讨论了计算参数的控制范围,并通过模型试验研究了迷宫堰自由泄流时所需的最小下游堰高;彭新民等[6]借助量纲分析法,结合模型试验结果,给出了迷宫堰流量系数的经验计算式,在其适用条件下具有较好的精度;马欣等[7]利用FLUENT软件,以V型迷宫堰为研究对象,重点研究了不同单宫角度对迷宫堰泄流的影响。
上述研究共同之处在于,迷宫堰在低水头工况下具有较高的过流能力,且工程投资相对于其他堰体型式的溢洪道较低,尤其是当工程受各种外部条件、建设规模有限等不利因素影响时,迷宫堰仍然可以满足功能需求。因此,该型式溢洪道越来越多地应用于改建、扩建及新建水库工程。
然而,现行规范中仍未对迷宫堰溢洪道设计做出具体规定,在实际工程应用时,迷宫堰设计参数一般根据经验估计,再进行模型试验加以验证。该过程持续时间较长,若各设计参数初步拟定不当,会引起工程设计及模型试验返工,造成工期及成本浪费,因此研究迷宫堰的水力特性、获得可靠设计参数对于工程设计具有重要意义。
1 工程概况
肯尼亚某中型水库溢洪道控制段原设计采用3孔8 m×5.5 m(宽×高)有闸宽顶堰结构。项目实施过程中,国际独立大坝专家组提出:考虑到肯尼亚当地供电保障率低、人员管理水平不高,采用电气控制泄洪在此区域风险较大。因此,肯方政府要求启动设计变更,改溢洪道控制段为无人操控的溢流堰结构。
1.1 设计条件
1.1.1 水 文
从水库淹没范围、工程效益、工程投资等方面比选,通过调洪演算,本工程确定的水库特征水位及流量见表1。

表1 水库特征水位及特征流量
1.1.2 工程地质
1.1.3 设计难点
保障水库特征水位及溢洪道设计下泄流量不变的基础上,避免产生额外征地、降低社会风险,维持溢洪道轴线及泄槽段不变,同时尽可能降低工程造价,在对比正向WES实用堰、侧向堰及迷宫堰后,迷宫堰所需总宽最小、工程投资最低、地基适应性最强,最终确定采用迷宫堰溢洪道方案。
1.2 迷宫堰设计
拟定迷宫堰底板顶高程及堰前进水渠渠底高程为1 851.0 m,堰顶高程为1 855.0 m,堰高p=4.0 m。迷宫堰由4个宫室组成,每宫宽w=9.0 m,总宽W=36.0 m,顺水流方向长度为15.0 m,总展长L=120.0 m,迷宫堰布置详见图1。控制段下游依次为收缩段、泄槽段、消力池段和海漫段。

图1 迷宫堰结构
迷宫堰过流能力按式(1)计算
(1)
式中:Q为计算下泄流量(m3/s);mw0为迷宫堰综合流量系数;W为迷宫堰总宽(m);g为重力加速度(9.81 m/s2);H为堰上水头(m)。
其中,迷宫堰综合流量系数随堰上水头的变化而变化,目前暂无相关设计规范或标准规定迷宫堰流量系数的取值或计算公式。根据国内外学者研究成果[8-10],采用插值法初步估计迷宫堰流量系数,见表2。

表2 迷宫堰综合流量系数估算
根据表2可知当w/p=2.25,H=2.40 m时,mw0=0.90;H=2.80 m时,mw0=0.82;进一步通过插值计算出PMF工况下,即H=2.75 m时,迷宫堰综合流量系数为0.83,相应下泄能力Q=603.5 m3/s,大于设计最大下泄流量,满足要求,按此方案进一步研究迷宫堰水力特性。
2 溢洪道泄流模拟
2.1 数值模拟步骤
Flow-3D是一款采用CFD解算技术、主要用于预测自由液面流动的仿真计算软件。该软件控制方程采用Navier-Stokes方程,针对研究的流体,利用软件独特的结构化矩形网格的FAVOR方法和广泛应用的Tru-VOF方法,建立适用于本次研究的三维水流RNGκ-ε紊流数学模型[11],其表达式如下。
连续性方程为
(2)
动量方程为
(3)
紊动能κ方程为
(4)
紊动能耗散率ε方程为
(5)

利用Flow-3D建立溢洪道数值模拟模型的基本步骤如下:
(1)创建工作空间与工程文件。
(2)模型建立与网格划分。数值模拟模型建立与网格划分主要步骤如下:①通用设置——对模型的计算时间、流体种类、单位、计算控制条件等选项进行设置;②物理模型设置——该菜单下包含各种物理参数、物理方程的选择与设置;③流体选定;④溢洪道模型建立与导入;⑤网格划分;⑥设置边界条件;⑦设置初始条件;⑧输出控制选项;⑨数值分析选项。
(3)求解分析。
(4)后处理。
2.2 迷宫堰溢洪道数值模拟
迷宫堰水流为三元流,因此必须采用三维仿真模拟分析。模拟分析以PMF工况为例,相关参数如下:PMF最高洪水位1 857.75 m;下游水位1 811.33 m;行进水头近似取为0;流体(水)认为不可压缩;重力加速度g=9.81 m/s2;流体温度20 ℃;流体黏性系数取0.001 03;流体密度为1 000 kg/m3;固体边界糙率为0.011。迷宫堰溢洪道数值模拟模型如图2所示。

图2 迷宫堰溢洪道数值模拟模型及网格划分
根据Flow-3D三维动态数值模拟结果可知,迷宫堰溢洪道泄流时水流过堰呈明显的三元流状态,过堰水流既从正堰过流,同时也沿两侧斜堰过流。当水流流过迷宫堰后,各向水流相互撞击,随后集中下泄。图3为迷宫堰溢洪道泄流流态稳定后,轴线处的水压及流速分布;图4为迷宫堰横截面处水压分布;图5为三维视角下迷宫堰泄流过程模拟。

图3 迷宫堰溢洪道水压分布和流速分布

图4 迷宫堰横截面处水压分布
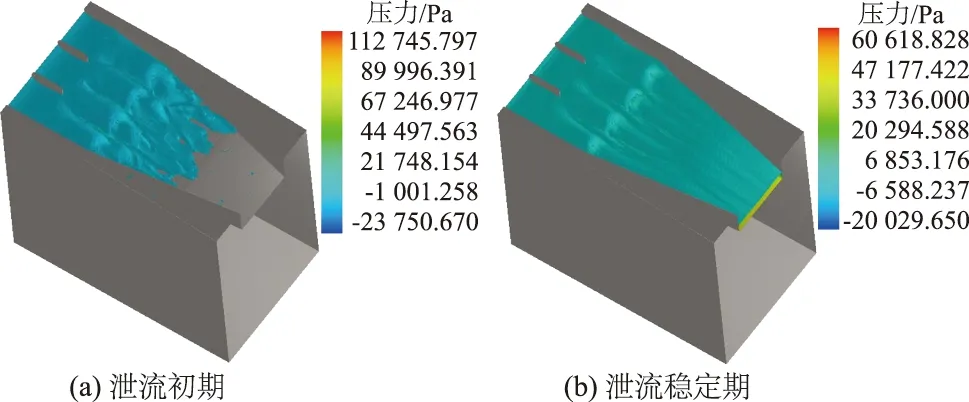
图5 迷宫堰泄流过程模拟
根据仿真模拟结果,PMF工况下,迷宫堰溢洪道泄流过程时,水压分布符合规律,最大压力水头为16.1 m,最大负压水头为1.7 m位于迷宫堰堰顶附近,其他部位负压水头均<1 m;表层流速大于底部流速,最大表层流速为22 m/s左右,主要集中于泄槽末端,收缩断面平均流速约15.6 m/s。泄槽末端断面收缩水深为1.8 m,平均流速为15.6 m/s,下泄流量为561.6 m3/s,满足设计泄洪要求。
3 迷宫堰模型试验
3.1 模型试验设计
根据数值模拟确定的迷宫堰设计参数开展模型试验研究。
3.1.1 模型试验任务
模型试验主要研究任务如下:
(1)验证数值模拟确定的迷宫堰的泄流能力。
(2)观测各工况下溢洪道上游引渠、控制端、泄槽段、下游消力池及出水渠的流态及水面线。
(3)测试溢洪道沿程流速、压力。
3.1.2 模型试验设计
根据《水工(常规)模型试验规程》(SL 155—2012)中的相似准则规定,本模型按正态模型设计,模型比尺为rL=40。相应的主要水力要素比尺如下:
流量比尺:rQ=rL2.5=10 119.289;
流速比尺:rV=rL0.5=6.325;
糙率比尺:rn=rL1/6=1.849 。
经验算,该比尺满足下述条件 :①模型水流进入阻力平方区;②模型水深在3 cm以上。
迷宫堰溢洪道模型如图6所示。

图6 迷宫堰溢洪道实体模型(迷宫堰处)
3.2 模型试验成果
迷宫堰溢洪道模型试验与数值模拟结果相似:下泄水流呈明显的三元流状态,过堰水流既从正堰过流,同时也沿两侧斜堰过流。当水流通过迷宫堰后,各向水流相互撞击,随后集中下泄。迷宫堰各宫室内水流流向沿溢洪道轴线方向而变化。
在低水头时,通过正堰和两侧斜堰的水流,其水舌处于完全通气状态,水流自由下泄,水舌的厚度和堰后水深对迷宫堰溢洪道的泄流能力不产生影响,流量系数随水头增加而增加。当堰上水头增大至0.83 m(相应水位1 855.83 m)时,通过上游侧正堰的水流首先受到两侧斜堰水舌的影响,难以通气,此时通过下游侧正堰的水流仍可继续通气,两侧斜堰过堰水舌仍为完整状态,并于水舌下方形成稳定气囊,此时流量系数达到峰值。当堰上水头进一步增大,水舌在整个堰顶的各部位均受到抑制,水舌下方原本稳定的气囊破碎,形成破碎的小气泡,并向上游移动,最后气泡完全消失,此时流量系数随水头增加而减小。
PMF水位时收缩段末端平均流速为8.19 m/s,泄槽末端水跃前断面平均流速为14.45 m/s;100 a一遇洪水时收缩段末端平均流速为8.07 m/s,泄槽末端水跃前断面平均流速为12.62 m/s;30 a一遇洪水时收缩段末端平均流速为7.74 m/s,泄槽末端水跃前断面平均流速为11.59 m/s;各水位下,消力池水跃均发生在消力池范围内,溢洪道沿程压力除30 a一遇迷宫堰堰顶为-0.96 m水柱外,其余均为正压,表明泄流流态良好。迷宫堰泄流流态如图7所示。

图7 不同特征洪水位下迷宫堰流态
试验测得迷宫堰水头-综合流量系数关系见图8,迷宫堰各库水位下的泄流量见表3。

图8 迷宫堰溢洪道水头-综合流量系数关系曲线
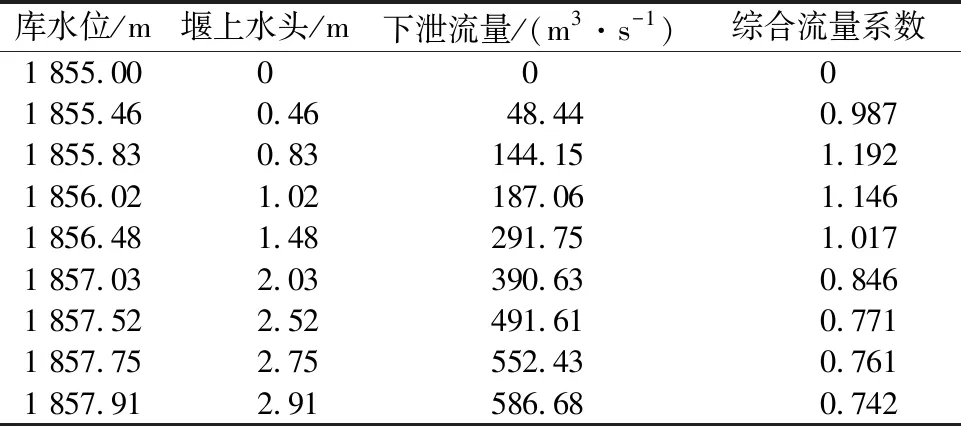
表3 迷宫堰溢洪道水位-流量
从上述数值模拟及试验结果可知,PMF水位时,迷宫堰泄量为552.43 m3/s,大于设计值。迷宫堰溢洪道具有较大的泄流能力,其综合流量系数随堰上水头的增加呈现先增后减的趋势,泄流时流态较为平顺,负压分布范围不大,表明本次设计参数合理、可靠。
4 结 论
通过对比、分析经验插值法、Flow-3D数值模拟及模型试验结果可初步获得如下结论:
(1)迷宫堰溢洪道泄流能力较高,尤其是在低水头工况下,采用该型式可明显节约工期和成本,且更适用于较为复杂的外部情况。但迷宫堰泄流时呈三元流状态,按经验法难以准确描述、计算其水力特性,必须采用模型试验验证。
(2)在低水头条件下,通过正堰和两侧斜堰的水流均可自由下泄,综合流量系数随水头增加而增加;当水头升至一定高度,正堰水流受到两侧斜堰水流影响难以通气,综合流量系数达到峰值;当堰上水头进一步增大,各部位水流均受到抑制,综合流量系数随水头增加而减小。
(3)Flow-3D数值模拟与模型试验结果基本吻合,按经验插值计算结果明显偏大,若直接采用,对工程安全不利;采用数值模拟与模型试验可以获得相对真实的泄流情况,可直观地读取泄流过程中水流的流态、流速、水头等重要参数,有利于进一步进行结构安全设计。
