余能回收水轮机叶片参数化设计与性能研究

李延频，刘安然，陈德新

（1. 华北水利水电大学 能源与动力工程学院，河南 郑州 450046； 2. 华北水利水电大学 水利学院，河南 郑州 450046）

0 引 言

输水管网为了避免因地势起伏造成管道超压或出于水量平衡调节的目的常设置减压阀［1-3］，使用微型余能回收水轮机将减压过程中消耗的压力能回收符合国家“双碳”战略。余能回收水轮机的工作环境和任务与常规水电机组不完全一致［4，5］，首先余能回收水轮机要优先保障管网的供水能力和调节的灵活性，其次应按照正常运行中可能出现的最大出力选择机组容量以避免频繁出现超负荷停机。目前，余能回收水轮机尚没有形成成熟的系列，需要根据不同应用场景的余能参数进行定制化设计［6］，传统设计流程中采用保角变换法对转轮叶片进行设计的操作过程较为繁琐。随着CAD 技术发展，国内外学者采用参数化设计方法实现转轮叶片的设计造型和优化。

朱尧华［7，8］指出水轮机叶片翼型参数化为造型提供了新思路、在优化方面有优势，并将参数化设计方法应用于轴流式水轮机叶片的三维设计。朱国俊等［9］采用Bezier 曲线参数化技术建立翼型的参数化表征方法。武桦等［10］采用B样条曲线来对叶片进行参数化并通过控制参数修改叶片形状。袁鹏等［11］采用儒可夫斯基保角变换的方法对翼型进行参数化建模和优化，提高了潮流能水轮机叶片升力系数和升阻比。DANESHKAH K等［12］描述了混流式水轮机转轮的参数化设计方法，指出用于描述三维叶片形状的参量对水力性能有直接影响。 FERRANDO L 等［13］将曲面参数优化应用于混流式转轮叶片的设计以节省设计时间并提高效率。魏雅静［14］通过对四次Bezier曲线翼型骨线的控制实现双向贯流式水泵水轮机转轮叶片的参数化。孙勤等［15］研究了三种翼型参数化方法包括型函数扰动法、控制点法以及复合映射法在翼型优化设计中的应用。陈婉春等［16］采用CST、FFD 和Hicks-Henne 型函数三种参数化方法优化翼型气动性能。王建军等［17］对HicksHenne 参数化方法进行改进并拓展该方法的参数化设计空间。阮辉等［18］采用逐点积分法对三种不同叶片安放角分布规律设计了冷却塔用低比转速混流式转轮叶片。目前，Bezier曲线容易保障整体的曲线的光滑，但是不便查看包角、安放角等重要的叶片参数，并且对曲线局部控制较弱。

本文所采用的参数化方法是建立在流线积分方程的基础上，用于转轮叶片的设计过程可以避免常规保角变换法的繁琐操作，并克服Bezier曲线查看包角、安放角不直观的缺点。参数化设计过程可简单分为三步，首先将轴面流线离散得到一系列微元段和轴面流线控制点，然后通过参数化方程对微元段进行计算，最终经过累加得到叶片骨线包角分布曲线及骨线控制点坐标。对骨线加厚得到转轮叶片并基于数值仿真对转轮内部流场和性能进行分析，结果作为叶片改进的依据，设计中通过改变叶片骨线包角曲线就可以实现叶片改型，可避免重复全部设计流程。文章最后通过试验检验了机组整体性能，研究成果为余能回收水轮机的设计提供了一种新的思路。

1 模 型

1.1 数学模型

传统设计方法中，叶片骨线通过轴面流线积分得到，其计算如下。

式中：S为轴面流线长度，m；ω为旋转角速度，rad/s；Vu为绝对速度的圆周分量，m/s；Vm为轴面流速，m/s；r为轴面流线上控制点到中轴线的半径，m；θ为叶片翼型骨线包角，rad。

根据速度三角形：

对式（1）进行离散，将轴面流线分为若干微元段，单个微元段叶片骨线包角、安放角和轴面流线微元段的归一化长度之间的关系算式如下。

式中：δθi为叶片骨线包角；βi为叶片骨线的安放角；为轴面流线微元段的半径归一化长度；δSi为轴面流线微元段长度；ri为轴面流线微元段到中轴线的平均半径。

将微元段包角累加即可得到叶片骨线的包角θ。

式中：θ0为叶片进水边的起始包角。

微元段的端点组成了轴面流线的控制点，通过式（5）进行设计，将叶片骨线的包角、安放角与控制点一一对应起来。设计过程中通过改变包角曲线容易实现叶片骨线的控制，变化幅度可定量设定，无需每次都重复全部设计流程。叶片骨线参数化设计流程见图1，计算过程见表1。

表1 参数化设计计算表Tab.1 The calculation table of parameters design

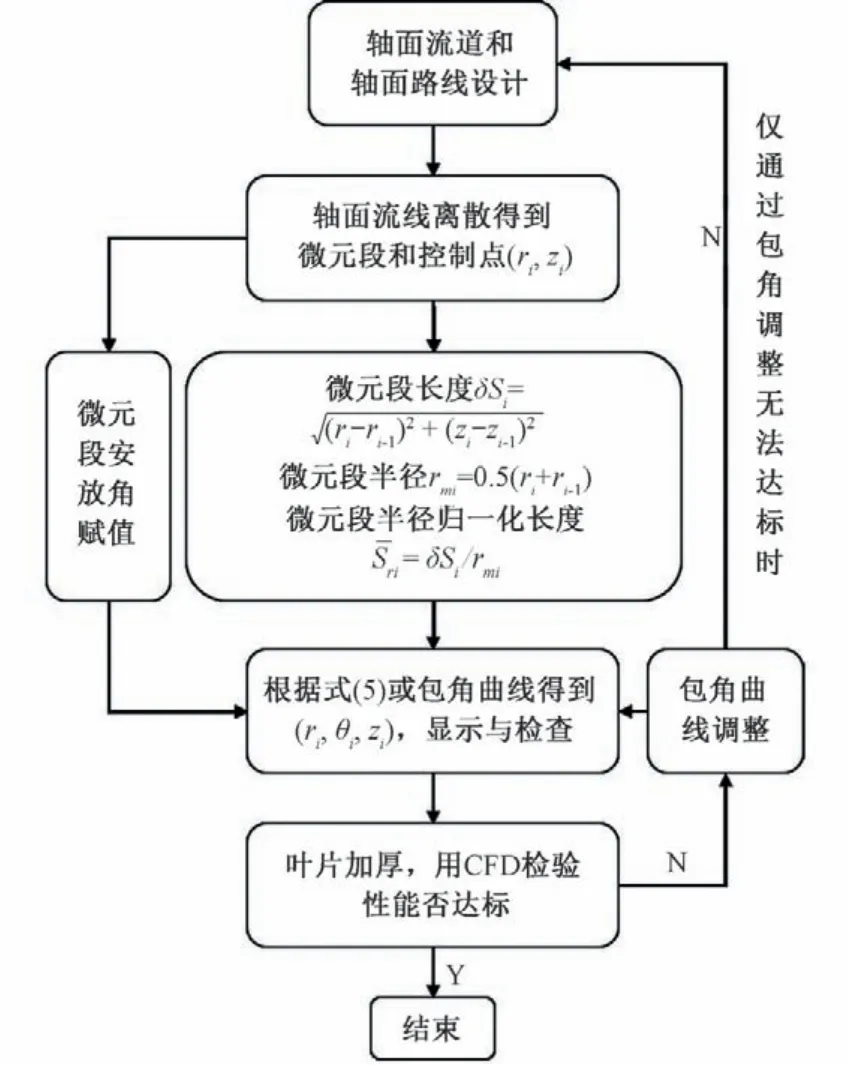
图1 参数化设计流程Fig.1 The process of parametric design

1.2 仿真模型

为降低微型余能回收水轮机的生产难度和成本，对过流部件适当地进行了优化，主要包括：①转轮叶片数宜适当减少并保证叶片厚度以满足整体铸造的工艺要求；②壳体包括蜗壳与尾水管一体铸造，蜗壳断面采用圆形且不设置固定导叶和隔舌，以降低铸造难度并避免蜗壳尾部杂物积聚；③余能回收水轮机串联在管路中，转轮出口水流保留一定压力以维持后续流动，尾水管一般简化为直锥型短管，动能恢复作用有限。因此，余能回收水轮机全流道仿真模型仅包括蜗壳、活动导叶、转轮和尾水管，如图2所示。

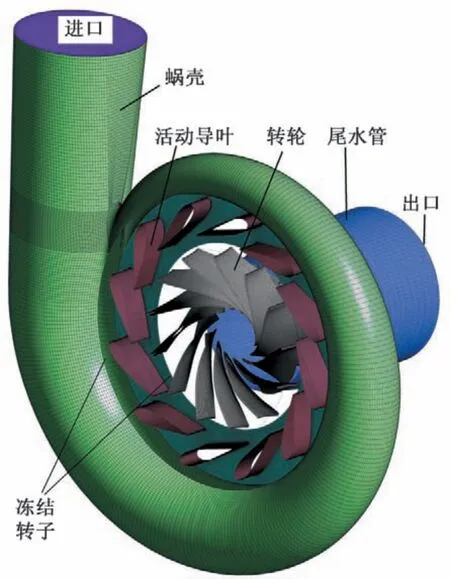
图2 余能回收水轮机全流道模型Fig.2 Full flow channel of hydraulic energy recovery turbine

选用商业计算软件CFX 对1∶1 模型进行数值仿真，全流道计算域平均划分为六面体网格，使用SST湍流模型，边界条件中进口设置为质量流量、出口为压力，不同计算域之间的交界面采用冻结转子，壁面设为无滑移。

2 结果与分析

2.1 参数化设计案例

某输水管网末端压力较高，经测量可利用压头约31 m，平均流量为720m3/h，采用余能回收水轮机进行发电回收富裕的能量，拟定余能回收水轮机设计工况见表2。

表2 余能回收水轮机额定工况参数Tab.2 Rated parameters of the hydraulic energy recovery turbine

首先基于一元理论得到轴面流线并分为若干段，然后按照参数化设计方法对每个微元段进行计算，最终得到叶片骨线坐标。按等厚度规律对骨线加厚并对翼型进出口边倒圆得到叶片翼型如图3，设计得到的叶片骨线包角曲线如图4。

图3 叶片参数化设计Fig.3 Parametric modeling of blade

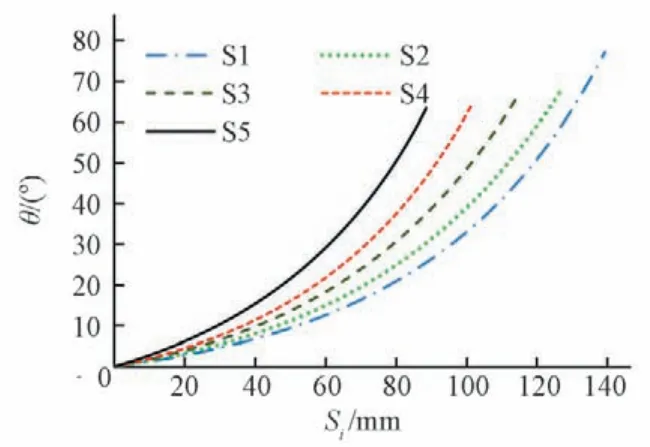
图4 叶片骨线包角曲线Fig.4 The wrap angle curves of blade

2.2 网格划分与无关性验证

通过数值仿真检验参数化设计得到的叶片，设计工况下蜗壳进口为质量流量为199.4 kg/s，尾水管出口的相对压力为0 Pa，转速为1 000 r/min。为保证计算精度对网格无关性进行验证，蜗壳和尾水管使用ICEM 划分六面体网格，导叶和转轮在TurboGrid 中划分，根据网格数量不同分为5种计算方案见表3，计算得到不同的方案下的水头预测值见图5。计算结果显示方案C 的网格数量达到394.1 万后水头预测值偏差小于0.25%，可认为此时网格数量满足无关性要求。

表3 计算域网格方案万Tab.3 Mesh number of flow domains in different cases

图5 水头预测Tab.5 Prediction of head

2.3 控制叶片参数曲线改变出口速度矩

叶片设计中的轴面流线和安放角等初始参数是根据一元设计理论得到，需要根据数值仿真分析结果多次调整叶片参数，参数化设计过程中已经保存了叶片包角、安放角等信息，可直接通过定量改变参数曲线控制叶片骨线。水轮机转轮出口速度矩分布对性能有影响，在设计工况下期望出口速度矩较小。数值仿真结果显示叶片出口靠近上冠处存在与转向同向的速度矩，为达到降低出口平均速度矩的目的，拟增加叶片出口边靠近上冠侧骨线包角。改型过程中要保持叶片整体的光滑，可以通过保证临近流线参数均匀变化实现。修改前、后叶片骨线参数曲线变化如图6，不同流面层上叶片骨线的包角是均匀变化的，改后叶片骨线仍然保持光滑，见图7。对比改变叶片参数前后出口速度矩分布曲线如图8，改后出口边平均速度矩从0.091 m2/s减小至-0.005 m2/s。

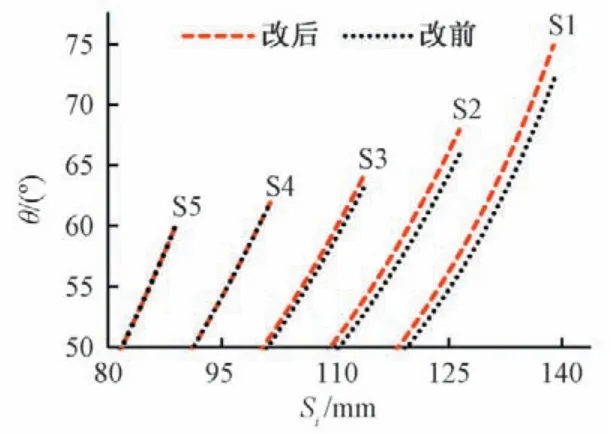
图6 改变叶片骨线包角分布曲线Fig.6 Change of the distribution curves of blade wrap angle

图7 叶片骨线变化对比Fig.7 Comparison of the difference between airfoil bone lines

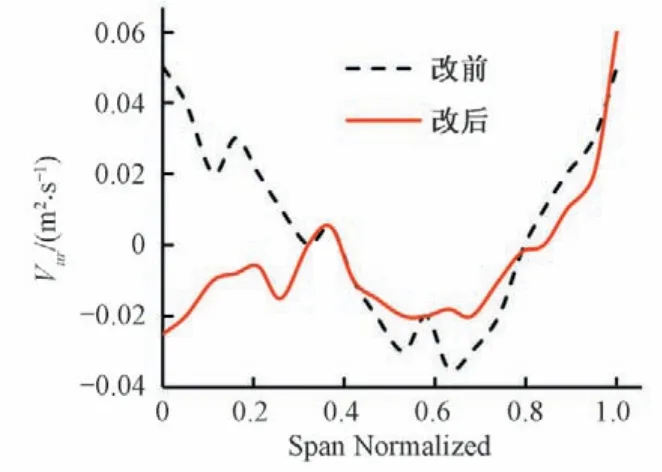
图8 出口速度矩分布曲线Fig.8 The distribution of velocity moment at runner outlet

2.4 内部流场与性能分析

对余能回收水轮机内部流场进行分析，速度矢量与压力梯度分布见图9，蜗壳内部流场分布均匀，在设计工况下，统计从蜗壳出口进入导叶各流道的流量分布规律如图10，结果表明不同流道之间的过流量偏差小于0.2%，所以蜗壳全部采用圆形断面并取消尾部隔舌板对性能影响不大。

图9 速度矢量与压力梯度分布Fig.9 Distribution of velocity and pressure gradient

图10 蜗壳出口圆周方向流量分布Fig.10 Distribution of flow rate at volute outlet circumferential

水流经活动导叶后形成与转轮进口相匹配的流场，叶片进口靠近压力面一侧具有低速流动区，并随着流动发展在叶道内部流场逐渐趋于均匀。转轮叶片进口高压侧低速流动区域可通过增加叶片数改善，但是微型余能回收水轮机叶片较厚，过多的叶片数会造成出口流道狭窄限制过流能力，采用长短叶片会加大铸造难度，最终选择13个叶片。统计余能回收水轮机各过流部件水头损失所占的比重，如图11，转轮水头损失最大，其次为导叶，水轮机全流道水力效率为93.6%。

图11 各计算域水力损失占比Fig.11 Hydraulic loss specific gravity of computional domains

2.5 试验验证

在流体机械通用试验台上进行真机测试，整体铸造的转轮如图12，试验系统组成见图13，试验过程中由循环泵提供带压水流，并通过变频和阀门联合调节以稳定水轮机进口水头，通过电磁流量计测量流量，发出的电能直接并入电网。

图12 整铸转轮Fig.12 Whole casting runner

图13 试验系统组成Fig.13 Consist of the test system

首先，将试验水头稳定在约31 m，调整导叶开度使过流量接近720±10 m3/h，记录平均发电功率约49.7 kW，机组的发电效率约为81.7%，根据异步发电机性能曲线查的效率约为92.5%，因此水轮机效率约为88.3±1.2%，与仿真结果相比，预测最优效率偏差达5.3%。造成偏差的可能原因首先是叶片表面粗糙度较高，其次是平压孔泄露和间隙泄露，另外还包括机械摩擦损失的影响。受生产工艺限制微型机组的效率与大机组相比有较大的差距，但基本可以满足使用要求。

3 结 论

对余能回收水轮机叶片进行参数化设计并通过数值仿真和试验验证，得到以下结论。

（1） 基于流线积分方程推导建立叶片骨线参数化计算公式，通过参数化设计将包角、安放角与叶片骨线控制点对应起来，具有操作简单、直观的优点。

（2） 参数化设计过程中保存了叶片参数数据，通过定量改变叶片参数曲线实现叶片形状的控制，实现了叶片出口速度矩分布的改变。

（3） 经参数化方法得到的水轮机全流道最优数值预测效率达到93.6%，实测真机效率约88.3%，基本满足使用要求。叶片参数分布规律与转轮性能之间的关系仍需要进一步研究。