改进的显随机动态规划在梯级水库优化调度中的应用

王 峰，王建平，王亦宁，郭希海

（1. 南瑞集团有限公司（国网电力科学研究院有限公司），江苏 南京 211106； 2. 国家电网有限公司东北分部，辽宁 沈阳 110180）

0 引 言

目前，大型水库常采用常规调度图来指导和制定中长期调度方案，而常规调度图一般是依据典型年或典型序列，通过模拟调度计算得到。该方法简单实用，易于操作，但存在着调度图局部较为粗略、正常出力区范围过大、没有考虑预报来水、调度策略具有较大经验性等不足之处，难以获得最优调度方案。

为了解决以上问题，可利用水库长序列发电运行资料，采用合适的优化调度模型，来制定水库调度规则，从而规避来水预报不确定性对水库调度的影响［1］。常用的水库调度规则优化方法包括隐随机优化调度法［2］和显随机优化调度法［3］，隐随机水库优化调度是将长序列径流资料作为水库来水过程描述，采用确定性优化调度模型求解最优运行过程，最后通过调度函数模型拟合水库运行要素与决策变量之前的关系，来指导水库调度运行，但优化规则的好坏受后期数据挖掘方法的选择影响较大，因此所获得的调度规则也无法达到最优效果［4］。显随机水库优化调度是将入库流量描述为随机过程，然后建立优化调度随机模型，求解得出水库优化调度规则。显随机优化调度在水库较多时，需要针对每个水库进行径流随机分级描述和决策变量离散，其模型求解会存在“维数灾”问题。

以东北第二松花江流域白山～丰满梯级水库水电站为例，研究中长期径流随机描述方法，针对不同径流描述情况，推导降维的梯级水库显式随机优化调度目标递推方程，并应用其求解成果制定梯级水库优化调度规则，指导水电站发电运行。白山、丰满两座水库调节性能都属于不完全多年调节，中间的红石水库为日调节性能，且区间集水面积较小，因此不作为此次研究对象。

1 梯级水库径流随机描述

水库的中长期天然来水过程具有一定的不确定性，而来水过程是水库优化调度模型的最重要输入，直接影响到优化调度模型的建立及求解。径流的随机描述方法包括随机独立、随机相关等模型，同时考虑到枯期径流具有时段相关性，可建立有、无时段预报相结合的径流随机描述模型。

梯级多个水库径流如果采用常规的逐个水库分级随机描述，将指数级增加优化调度模型的计算量。而同流域的梯级水库天然径流具有较强的相关性，可依此来寻求简化的描述方法。现有白山、丰满以及区间1933 至2021 年的逐月天然径流资料，分析径流间的相关关系，同时段丰满与白山径流关系、丰满与白丰区间径流关系分别见图1、图2，通过一阶回归方程对径流进行模拟，采用10%的变幅误差进行准确率评定，计算结果见表1。分析得出丰满与白山、丰满与白丰区间径流均有非常强的相关性，因此针对分析丰满的径流描述方法，白山、白丰区间同时段径流可通过丰满径流计算得出，从而达到降维的效果。

表1 丰满与白山、白丰区间径流模拟结果Tab.1 Runoff simulation results of Fengman and interval

图1 同月份丰满与白山径流关系图Fig.1 Runoff relationship between Fengman reservoir and Baishan reservoir in the same month

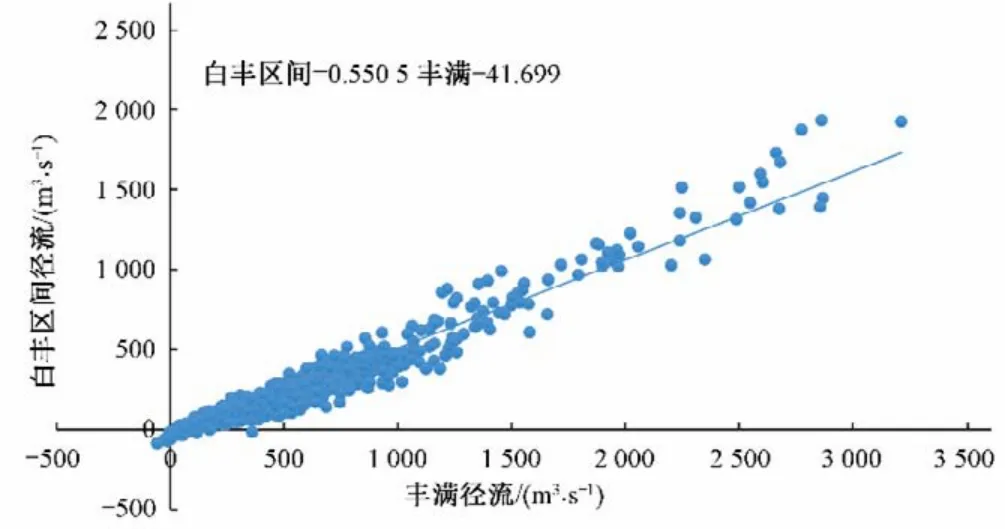
图2 同月份丰满与白丰区间径流关系图Fig.2 Runoff relationship between Fengman reservoir and interval in the same month

据丰满水库资料情况，按月将年内划分为12 个时段，顺序标号各时段。根据马尔科夫链适用条件的检验方法［3］，对径流序列进行相关分析，结果见表2。

表2 丰满径流序列相关关系Tab.2 Correlation of Fengman runoff series

针对每个月份建立丰满径流上一个时段Qt-1与当前时段Qt的一阶回归模拟模型，并以1933 至2011 年径流资料作为输入训练模型，余留的2012-2021 年径流资料用来检验模型。以20%的变幅误差进行准确率评定，评定结果见表3。

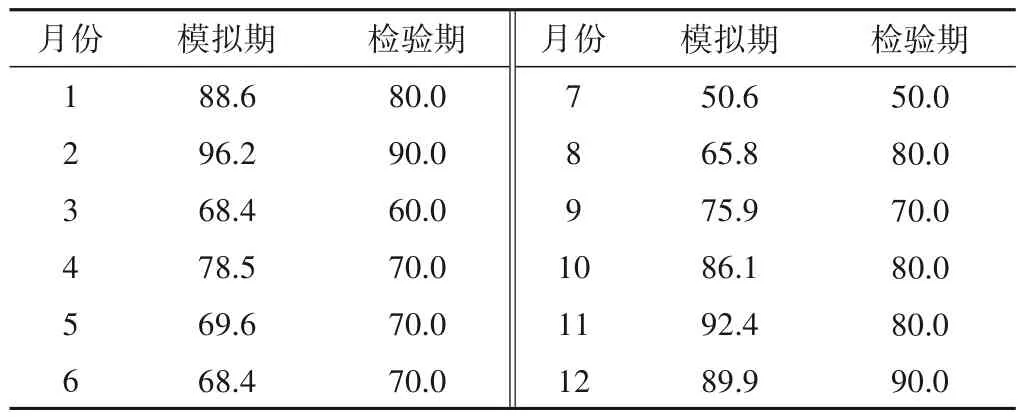
表3 丰满径流各月模拟准确率%Tab.3 Monthly simulation accuracy of Fengman runoff

根据模拟结果，选择模拟准确率和检验准确率都在80%以上的时段，即1、2、10、11、12等月份采用有预报的马氏链径流描述模型，其他时段采用无预报的马氏链径流描述模型，这种有、无时段径流预报相结合的马氏链径流描述模型更加符合实际情况。采用等概率方法对各时段径流进行分级，径流状态转移概率矩阵的求解方法［5-10］。

2 随机优化调度模型建立

对于一个调度时期(1…t- 1，t，t+ 1…T)，采用顺序进行编号，t代表当前时段，t-1代表上个时段，t+1代表下个时段。

2.1 状态变量及决策变量的确定

对于梯级水库随机优化调度，t时段的决策状态变量由各水库径流状态及水库水位组合确定，且根据有、无时段径流预报，径流状态也有所不同。根据白山～丰满梯级水库的径流描述，白山、白丰区间径流状态均可由丰满径流计算得出，因此，当t时段无径流预报时，本时段径流由上时段径流状态确定，即状态变量为：

当t时段丰满有径流预报时，梯级水库状态变量为：

调度决策变量可选择逐时段各个水库的水位、出库流量、发电出力，本文选择时末水位作为决策变量，离散的水位可供时段初状态判断、时段末决策计算同时使用，便于程序求解实现。根据白山、丰满两座水库的特性，从死水位到正常高水位，按照0.5 m 的间隔，对两座水库水位进行离散，离散值分别为67个和39个。

2.2 调度模型的建立

在以一定保证率满足梯级电站保证出力的前提下，追求调度期内发电量期望值最大作为优化调度模型的目标函数。目标函数的计算与径流描述有关，根据上述白山～丰满梯级水库有、无时段预报相结合的径流描述模型，目标函数的递推公式将分为4种情况，见表4。

表4 各月份径流描述情况Tab.4 Description of runoff in each month

研究根据4 种情形，分别建立目标函数的递推公式。公式中Et代表当前时段t至调度期末的发电量期望值，Et+1是余留期发电量期望值，et当前时段t的发电量，pt为t时段的径流转移概率，Z代表水库水位，Q代表径流量，n代表各时段丰满的径流状态，m 代表各时段白山的径流状态，l 代表各时段区间的径流状态。

2.2.1 相邻时段无径流预报时递推方程

常规的非降维径流描述模型，对应的递推方程如下：

针对本文径流描述模型，此时水库的运行状态见式（1），由于当前时段t无径流预报，所以当前径流需考虑上个时段t-1径流相关关系下的各状态，每种状态分别搜寻白山、丰满的时段末水位来计算最大发电量，然后求得电量期望值。模型的递推方程如下：

式中，梯级电量为白山、丰满的电量之和，即：

根据径流描述，白山以及白山～丰满区间天然径流可通过丰满天然径流计算得到，丰满的实际入库等于白山出库与区间流量之和，即：

2.2.2 相邻时段有径流预报时递推方程

常规的非降维径流描述模型，对应的递推方程如下：

针对本文径流描述模型，此时水库的运行状态见式（2），当前时段t已有径流预报，可直接计算得出电量，由于本模型仅考虑一个时段有径流预报，对于下个时段的电量计算，需要考虑当前径流相关关系下的各状态径流，以电量期望值作为预留期电量。模型的递推方程如下：

2.2.3 本时段无预报且后时段有预报时递推方程

常规的非降维径流描述模型，对应的递推方程如下：

针对本文径流描述模型，此时本时段的运行状态为式（1），后时段的运行状态同式（2）。在寻求最优决策水位时，由于当前时段t无预报，所以要考虑本时段各个概率下的径流状态；同时，后时段t+1有预报，需要考虑当前径流相关关系下的各状态径流。递推方程考虑了两个时段径流状态的组合，如下：

2.2.4 本时段有预报且后时段无预报时递推方程

此时，本时段的运行状态为式（2），后时段的运行状态同式（1）。当前时段t有预报，时段电量根据决策水位和预报流量直接求出；而后时段t+1无预报，其运行状态都由当前时段t决定，余留期电量公式可直接得出。模型的递推方程如下：

2.3 模型约束及求解

2.3.1 模型约束条件

由于调度模型目标选择的是发电量最大，在求解计算过程中，为了追求低耗水率，算法会把水位抬高后再发电，这将导致有些时段发电量很小，甚至不发电，所以必须考虑保证出力的影响。本文采用利用惩罚和改变保证出力约束相结合的方法［11，12］，可得到各种出力保证率下的水库最优决策方案。

此外，水库调度收到多种约束条件的影响，研究综合考虑了水量平衡、最低/高运行水位限制、预想出力限制、最小/大出库限制等约束，约束处理办法见参考文献［11，12］。

2.3.2 模型求解

显式随机优化调度模型求解需要以年为周期进行多时段马尔科夫决策寻优，且在一个调度期内梯级水库状态和决策还需进行逐一组合计算，其运算量是非常巨大的，本文采用随机动态规划算法求解模型，具体方法见参考文献［13-16］。

模型求解过程中，每年各个时段、各个水库、各个状态下对应的最优决策水位为当年的求解结果，当求解结果趋于收敛，且逐年连续稳定不变，或者变化满足设定的精度要求，模型即可中止递推，最后一年的结果就是最优的调度规则。

3 模拟调度及结果分析

为了对比分析，除本文得到的优化调度规则外，还将以常规调度图、传统的无径流预报随机优化调度规则以及非降维的随机优化调度规则，分别指导白山、丰满梯级水库“89 年”的历史径流序列进行模拟调度，各方案描述如下：

方案一：以常规调度图指导历史序列进行模拟调度，得到一定时段出力保证率下的水电站运行过程。

方案二：采用本文的径流描述方法和调度模型，调整保证出力惩罚系数，可求解得到与常规调度图相同出力保证率的白山～丰满梯级水库各状态下的最优调度决策规则集。以此规则指导历史径流序列进行模拟优化调度，并得到逐年的发电量。本文称该方案为主方案。

方案三：为分析预报误差对径流描述的影响，对有预报时段的径流采用实际值，并进行模拟调度。

方案四：为分析有、无时段径流预报描述模型的合理性，采用各时段都无径流预报的常规随机优化调度模型和同样的约束调节，求解得到相应的调度规则，并进行模拟调度。

方案五：为达到降维计算目的，采用梯级总来水（丰满入库径流）作为分析对象，实际输入的白山入库、区间流量径流状态通过计算得出。为分析此径流描述带来的影响，采用常规的非降维随机径流描述方法，求解得到优化调度规则，并进行模拟调度。

各调度结果方案见表5，各方案与主方案的结果对比图见图3。方案一与方案二模拟调度运行的多年平均月初水位见图4。

表5 不同方案模拟优化调度结果Tab.5 Simulation dispatching results of different schemes

图3 各方案与主方案的结果对比图Fig.3 Comparison of results between each scheme and the main scheme

图4 白山、丰满模拟运行多年平均水位图Fig.4 Average water level of simulated operation for many years

对比分析表5、图3和图4可得出：

（1） 与常规调度图的模拟调度结果（方案一）相比，方案二、方案四分别增发电量2.55 亿kWh 和1.18 亿kWh，增长率为6.8%和3.15%，说明了随机优化调度模型的有效性；

（2） 与常规的无径流预报随机优化调度模拟结果（方案四）相比，方案二每年多发了1.37 亿kWh，说明针对白山～丰满梯级水库的径流描述模型更加贴近实际，优化调度得到的调度规则能更好地指导水库运行。

（3） 方案三比方案二对多发了0.99 亿kWh 电量，表明有预报时段的预报误差对调度结果产生了一定的影响，同时也说明了随着径流预报精度的提高，相应地改进有预报时段的径流描述模型，还有一定的发电效益提升空间。

（4） 方案五比主方案仅多发了0.04 亿kWh 电量，这是因为本文研究的梯级水库对象其总径流与白山入库、区间径流有很强的相关性，且随机优化调度模型采用分级的状态径流作为输入，该描述方法对实际影响较小，说明本文降维径流描述模型的合理性。

（5） 在优化规则求解上，对比非降维的模型递推方程可以看出，由于径流状态少了一维，简化了编程实现，降低内存溢出可能性，求解速度也得到了大幅提升。

（6） 对比优化规则与常规调度图模拟运行多年平均水位图可知，两座水库的蓄满时间相对滞后，且保持了较长时间的高水位运行，使得水头效益充分利用，增加了发电量。

4 结 语

针对白山～丰满梯级水库的实际径流特性，提出了基于降维的马尔科夫链随机径流描述模型，解决梯级水库随机优化调度模型求解的维数灾问题；同时结合有、无时段径流预报的描述方法，使得径流描述更加贴近实际。

根据径流描述方法建立梯级水库随机优化调度模型，逐一分析和创建相邻时段有预报、相邻时段无预报、本时段无预报且后时段有预报、本时段有预报且后时段无预报等四种情况的模型递推方程，并递推优化计算得到调度规则。通过对白山～丰满梯级水库“89年”径流序列进行模拟优化调度可以得出，在相同的出力保证率情况下，本模型产生的调度规则比常规调度图以及传统无预报随机优化调度规则，平均每年增发电量2.55亿kWh和1.37 亿kWh，验证了本文所提出模型的优越性。随着水文预报技术的提升，以及中长期径流预报精度的提高，可相应地改进本文所提出的梯级径流描述模型，将会得到更优的水库调度规则。同时，随着智能求解算法的成熟应用，也可解决维数灾问题，智能算法与传统算法的对比、相结合应用，也是下一步的研究方向。