考虑渗流作用的闸坝深层抗滑稳定性分析
2023-08-28胡怿兴
胡怿兴
(湖南省水利水电勘测设计规划研究总院有限公司,湖南 长沙 410007)
0 引 言
闸坝是一种调节水位、控制流量的低水头水工建筑物,具有挡水、泄水、引水和防洪等功能,在水利水电方面用得非常广泛。其基础中往往不可避免地分布着一些不利的节理、裂隙和软弱结构面,应进行结构沿软弱结构面的深层抗滑稳定计算研究[1-3]。传统此类结构的深层抗滑稳定性分析采用双画面的等K法,但是此方法受限于软弱结构面分布的不确定性,深层抗滑稳定往往需要进行大量的敏感性分析和各种组合分析,计算量很大。有限元强度折减法[4,5]采用弹塑性理论,不需要人为地假定滑动面,就可以真实地求出最危险滑动面,是一种更为先进的计算方法。目前关于有限元强度折减法的研究主要集中在结构失稳判定准则[6-8]和弹塑性本构模型屈服准则[9,10]等方面,而在应用方面主要为三维边坡[11,12]和隧洞[13]等结构稳定性分析的探索,缺乏在实际工程中的应用,特别是岩土材料中有明显水活动的应用案例。事实上,对于一些大型通用有限元软件ANSYS、ABAQUS和ADINA 等[14-16]可以方便地实现强度折减法,但是如何考虑水的影响仍然有待进一步研究。
已经有一些的研究表明,建筑物基础中水的活动应该作为场力考虑。张有天[17-19]从连续介质渗流理论出发,对岩土中的渗流荷载进行了推导,渗流荷载是体积力,并将其分解为渗透体积力和浮托力,并将其用于隧洞外水压力的计算研究。毛昶熙[20]对渗透场力的物理概念进行了论述,引用格林公式,证明土体表面水压力与土体本身渗透力之间的准换关系,并应用到管涌和滑坡问题的研究。尹晓萌等[21]针对在地下水作用力使用中易出现力的概念混淆,重复计算的问题,论述了土体中的空隙水压力、浮力、渗透力3 种地下水作用力的性质,可为具体工程项目的应用提供参考。本文以犬木塘水利枢纽泄水闸为研究对象,在有限元强度折减法的基础上,通过渗透场力的方法,实现了渗流场-应力场的耦合,单向地考虑了渗流场对应力场的影响,未考虑应力场对渗流场的影响,重点研究了渗流作用对结构深层抗滑的影响。从基础帷幕灌浆效果,单独考虑渗透体积力和浮托力,同时考虑渗透体积力和浮托力几个方面,研究了渗流作用下闸坝的深层抗滑稳定性。
1 工程实例
1.1 工程概况
犬木塘水库工程是解决“衡邵干旱走廊”水资源短缺问题的骨干水利工程,开发任务以灌溉为主,结合城乡供水,兼顾灌区水生态环境改善以及航运、发电等综合利用,工程为Ⅱ等大(2)型水利水电工程,枢纽部分厂房、船闸、泄水闸、连接坝等主要建筑物坝身及上游挡水部位为2 级建筑物。17 m×10.5 m(宽×高)平底闸,弧形闸门挡水,闸墩厚3.0 m,堰顶高程204.5 m,闸墩顶设跨径4.2 m 的坝顶门机及14.5 m 宽Ⅱ级公路桥。设计水位215.00 m,与之对应的下游最低水位206.00 m。
坝区岩层近横河向,整体倾向下游,倾角15°~25°,倾角较缓,且顺层面发育有较多的软弱夹层(坝轴线上泥化夹层5条),夹层性状差,地表及钻孔取芯多呈泥或岩屑型,易软化,软化后多呈泥状,手可捏动,其抗剪强度低,对坝基抗滑稳定不利,在受到上部荷载及水压力等外界因素综合作用下,坝基块体有可能顺层面、软弱夹层面剪切,沿节理或岩体本身等部位剪出,可能存在坝基深层抗滑稳定问题,因此需进行坝基深层抗滑稳定计算。
1.2 有限元模型
整体三维有限元模型坐标系为:X向为坝轴向;Y向为顺河向;Z向为竖直方向。模型地基模拟范围上游向为100 m,下游向从消力池末端起70 m,深度方向取到地面以下100 m,横河向X方向的计算范围宽度为21 m。整个有限元模型共离散结点179 357 个,单元159 635 个,整体有限元模型如图2所示。
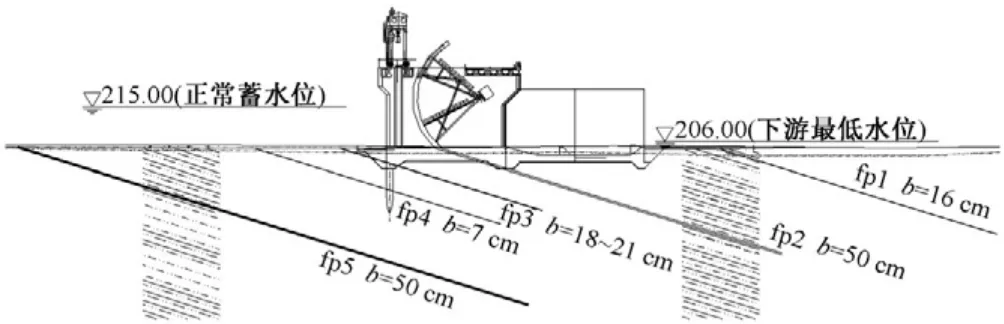
图1 闸坝设计断面及基础软弱结构面分布图Fig.1 Design section of gate dam and distribution of soft structural surface of foundation
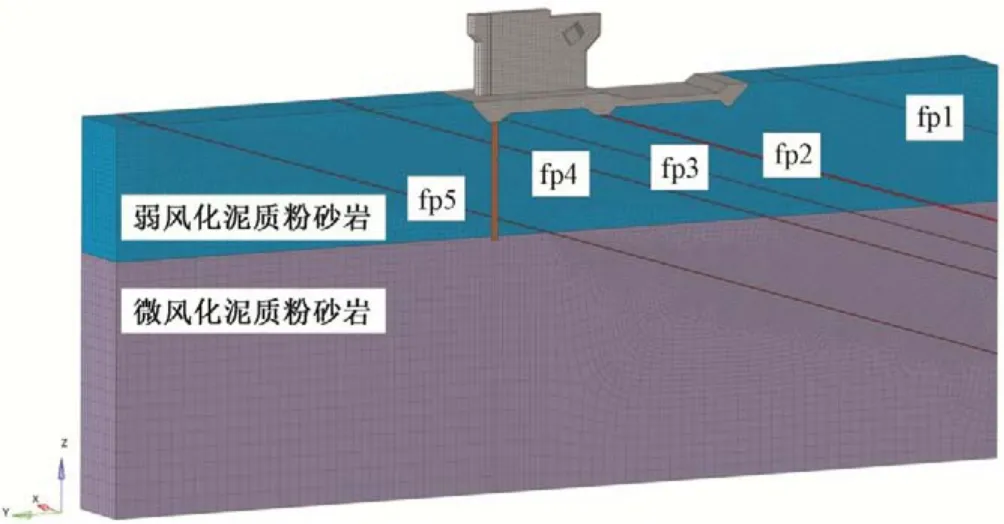
图2 闸坝三维有限元计算网格图Fig.2 Three dimensional finite element calculation grid of sluice dam
1.3 材料参数及边界条件
计算范围内的主要材料为弱风化、微风化泥质粉砂岩、混凝土、帷幕灌浆和泥化夹层,深层抗滑计算采用有限元强度折减法,岩土材料采用摩尔库伦本构模型,闸坝结构材料为C25混凝土,采用线弹性本构模型,主要力学参数如下表1所示。边界位移约束条件为:坝轴向两侧基础截断边界处X向约束,顺河向两侧基础截断边界处Y向约束,地基底部Z向约束。
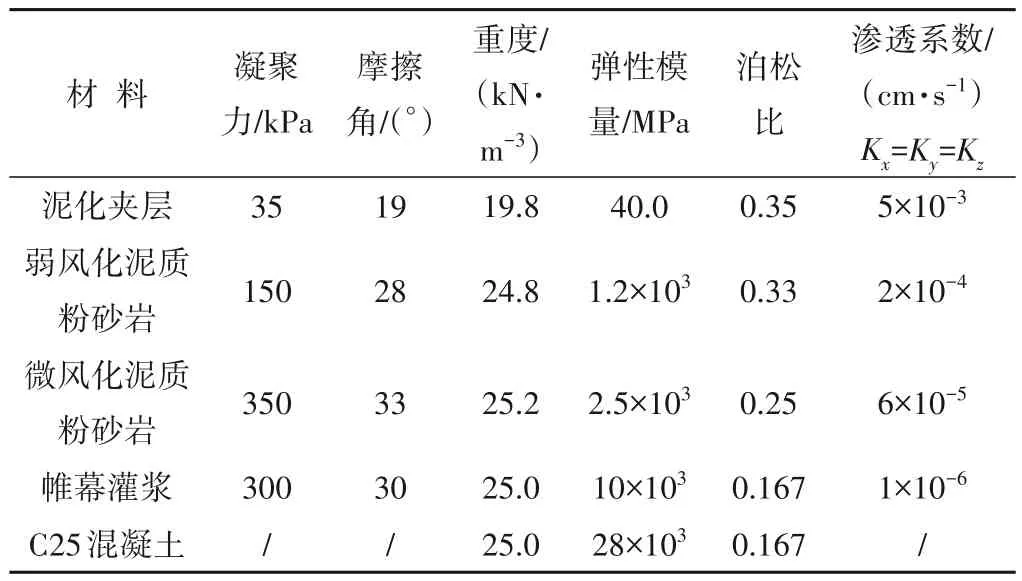
表1 主要材料物理力学参数表Tab.1 Parameters
2 渗流场有限元求解
2.1 渗流计算
非均质各向异性多孔隙介质中的稳定饱和渗流连续微分控制方程为:
式中:ϕ为总水头;x、y和z为空间坐标;Kx、Ky和Kz三向渗透系数,本文算例中假定三向渗透系数相等。
由于混凝土为相对不透水材料,故渗流计算模型不考虑闸坝材料单元。建基面按照不透水边界考虑,上、下游侧分别设置对应水位的总水头边界。渗流计算模型的结点和网格编号需要和深层抗滑稳定有限元计算的模型结点和网格编号一致,渗流计算模型见图3。
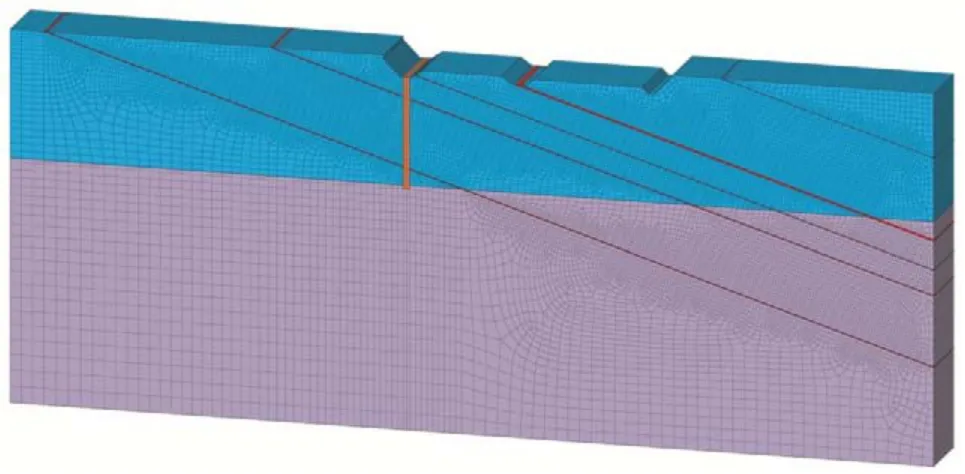
图3 闸坝三维渗流有限元计算网格Fig.3 Three dimensional finite element seepage calculation grid of sluice dam
2.2 渗流计算结果
图4 分别给出了闸坝基础的稳定渗流计算结果,地层上部为强风化泥质粉砂岩,且分布着5 条泥化夹层,透水性较强,帷幕灌浆至微风化层,将上部强透水层截断。
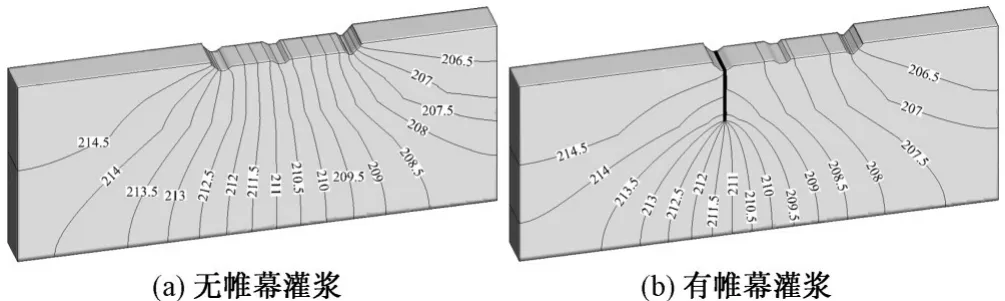
图4 闸坝基础总水头等值线图(单位:m)Fig.4 Contour graph of total head
2.3 渗透场力
总水头H:
式中:p为水压力;γ为水容重;z为竖向坐标。
渗流场力:
式中:前一部分{ -γJx, -γJy, -γJz}为渗透体积力,渗透体积力与水力梯度成正比,Jx、Jy、Jz分别为单元在x、y、z方向的渗透坡降;后一部分{γ, 0, 0}为浮托力。
依据有限元数值分析方法,得到渗流体积力后,通过下面的式子将单元的渗透体积力转化为对应的节点等效荷载:
式中:{FS}为渗透体积力引起的等效节点力;[N]为单元形函数。
3 深层稳定分析
3.1 有限元强度折减法原理
有限元强度折减法是将岩土材料的抗剪强度除以折减系数后用于有限元弹塑性计算,取结构达到破坏时的折减系数为安全系数。假定岩土体的强度参数为c和ϕ,试算所取折减系数为Fr,则折减强度τr为:
则岩土材料的折减强度参数cr、ϕr的计算表达式为:
有限元强度折减法的失稳判断主要有以下几种类型:①计算不收敛;②塑性区贯通;③位移突变。由于本文分析的闸坝的深层抗滑,涉及到的荷载等边界条件较为复杂,单凭任一失稳判断依据并不能准确地描述结构稳定性,本文将综合考虑3种失稳判断依据,作为结构最终失稳判断的依据。
3.2 计算工况及计算结果分析
表2 给出了不同工况下深层抗滑稳定安全系数表,图5 为相应的位移变化曲线,图6 为各工况下等效塑性应变云图。由图表可知,考虑帷幕灌浆的结构深层抗滑稳定系数在各种情况下均大于不考虑帷幕灌浆的情况,主要是由于:帷幕灌浆一方面有效降低了滑面处的扬压力;另一方面也是由于帷幕灌浆提高了灌浆区的岩体力学指标,增强了结构的深层抗滑稳定性,另外,在安全系数未折减时,考虑帷幕灌浆情况的位移为6 mm,小于不考虑帷幕灌浆情况的14 mm。横向对比不难发现,无论是否考虑帷幕灌浆,结构的深层抗滑稳定安全系数规律表现为,单独考虑渗透体积力>单独考虑浮托力>同时考虑渗透体积力和浮托力,由此可见,浮托力起主导作用,但是渗透体积力的作用不可忽视。

表2 不同工况下深层抗滑稳定安全系数表Tab.2 Safety factors of deep anti sliding stability under different cases

图5 位移—强度折减系数关系曲线Fig.5 Relation curve of displacement strength reduction coefficient
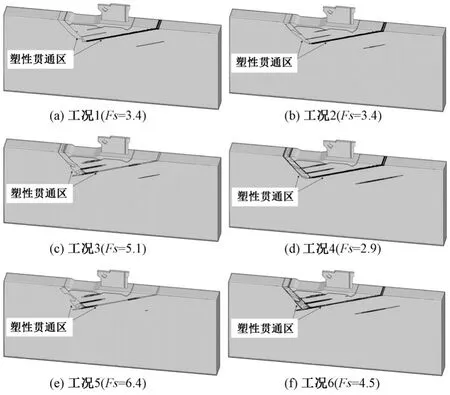
图6 等效塑性应变等值线图Fig.6 Contour graph of equivalent shear plastic strain
4 结 论
本文结合具体工程实例,在有限元强度折减法的基础上,通过渗透体积力的方法,研究了渗流作用下闸坝的深层抗滑稳定性,得到以下结论。
(1)基础帷幕灌浆可有效截断渗流,显著提高闸坝结构深层抗滑稳定性;
(2)无论是否考虑帷幕灌浆,结构的深层抗滑稳定安全系数规律表现为,单独考虑渗透体积力>单独考虑浮托力>同时考虑渗透体积力和浮托力;
(3)渗透体积力和浮托力对结构的稳定性都是不利的,浮托力起主导作用,但是渗透体积力的作用不可忽视。
