水轮机空化声发射信号降噪与混沌图像特征提取

2023-08-28刘忠李显伟邹淑云王文豪周泽华

哈尔滨工程大学学报 2023年8期

刘忠, 李显伟, 邹淑云, 王文豪, 周泽华

(长沙理工大学能源与动力工程学院,湖南长沙 410114)

水电作为一种可再生能源受到国内外的关注。作为主要能量转换设备[1-2],水轮机内部发生空化时,会损坏过流部件,降低机组效率,严重时会产生强烈振动,从而影响机组安全稳定运行[3]。空化发生时,大量空泡溃灭会在短时间对水轮机叶片和流道内壁产生冲击,沿水轮机机械结构传播出高频声发射(acoustic emission,AE)信号[4]。为了准确识别水轮机空化状态,对空化AE信号处理显得尤为关键。针对信号含大量噪声影响特征提取效果的问题,一系列降噪方法相继提出。经验模态分解及其改进方法仍存在模态混叠弊端[5-6],小波阈值降噪及变分模态分解方法依赖于关键参数的选取[7-8]。相较而言,傅里叶分解方法(Fourier decomposition method,FDM)优势明显,其分解原理基于傅里叶变换,对非线性信号能够进行完备的、正交的自适应分解,克服了端点效应、模态混叠、非自适应方法参数确定等问题[9]。由于采集到的水轮机空化AE信号受现场环境等因素影响包含一些噪声,采用FDM方法可将其自适应分解,利用相关系数法直接剔除一部分噪声分量,对同时包含噪声和有用信息的另一部分分量未作处理。而多分辨奇异值分解方法(multi-resolution singular value decomposition, MRSVD)利用噪声和有效信息的奇异值分布特性,可对这些分量进行降噪[10]。水轮机空化AE信号具有典型的非线性和非平稳性[11]。采用混沌理论中最大Lyapunov指数、关联维数等参数可以定量描述空化严重程度,并且证实了水轮机空化AE信号具有混沌性[12]。然而,采用混沌特征图像表征水轮机空化AE信号并研究其演变规律的文献并不多见。

本文利用FDM方法的优势对水轮机空化AE信号进行完备分解,再采用MRSVD方法对同时包含噪声和有用信息的分量进行降噪,应用混沌理论重构相空间以挖掘水轮机空化AE信号内在信息,构造相轨迹图及Poincaré截面图。

1 信号降噪及特征提取涉及的算法

1.1 FDM算法

FDM算法可将多分量随机信号x(t)分解为:

(1)

式中:yi(t)为分解得到的W个单分量信号;λ(t)为残余分量。FDM分解方式有从高频到低频HTL-FS和从低频到高频LTH-FS共2种方式。LTH-FS在高频段具有较好的时频分辨性,HTL-FS在低频段具有较好的时频分辨性。根据水轮机空化AE信号的噪声分布特点,选择HTL-FS方式,具体步骤为[13]:

1)对多分量信号x(n)进行傅里叶变换得到时间序列矩阵X(k),即:

X(k)=FFT{x(n)}

(2)

式中FFT为快速傅里叶变换函数。

2)HTL-FS算法求解解析傅里叶固有频率带函数(analytic Fourier intrinsic band functions,AFIBFs):

ai(n)exp[jφi(n)]

(3)

式中:i=1,2,…,M;N0=N/2;NM=1;N为信号长度。HTL-FS搜索方法在保证信号完全分解的同时获得最少数目的,对于任意i个AFIBFs分量,傅里叶固有频带分量的叠加数目从Ni-1-1开始逐渐减小到Ni,1≤Ni≤Ni-1-1。且均满足单步差分的假设条件要求AFIBFi的相位时变幅值φi(n)始终为一个单调递增函数,即:

(4)

3)计算残余分量λ(n):

λ(n)=X(0)+X(N/2)(-1)n

(5)

4)求解AFBIFs的瞬时频率,实部即为傅里叶固有频带函数(Fourier intrinsic band functions,FIBFs)。

1.2 MRSVD算法

MRSVD将矩阵二分递推构造法和奇异值分解算法相结合,能够将信号分解为多个层次的子信号。图1为MRSVD分解过程图。

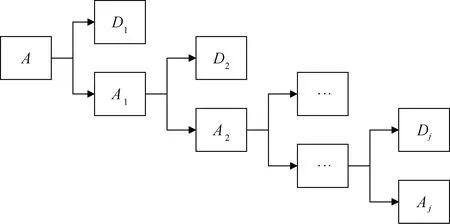
图1 MRSVD分解Fig.1 MRSVD decomposition process

MRSVD具体步骤为[14]:

1)对任意信号X={x1,x2,…xn},应用二分递推法分解理论将其构造成Hankel矩阵H:

(6)

2)对矩阵H进行奇异值分解,分别计算2个重构子信号的奇异值。第1次分解得到的近似信号A1为较大奇异值对应的重构子信号;第2次分解得到的细节信号D1为较小奇异值对应的重构的子信号;

3)将近似信号A1继续应用二分递推法构建Hankel矩阵,进行奇异值分解。

MRSVD的降噪性能较好,正常信号和噪声信号由于相关性不同导致其奇异值分布差异,结果使得噪声信号被分解在细节信号中,正常信号被分解在近似信号中。在分解开始时,细节信号奇异值急剧降低,这说明噪声分离在刚开始时速度较快,随后逐渐平稳。说明当分解层数增多时,噪声的消除会减慢,最终趋于不变时,分解终止。获得第j次的近似信号Aj为经过降噪处理后的信号。

1.3 FDM-MRSVD降噪

建立基于傅里叶分解方法和多分辨奇异值分解方法相结合的FDM-MRSVD降噪方法,其流程图见图2。其主要步骤为:

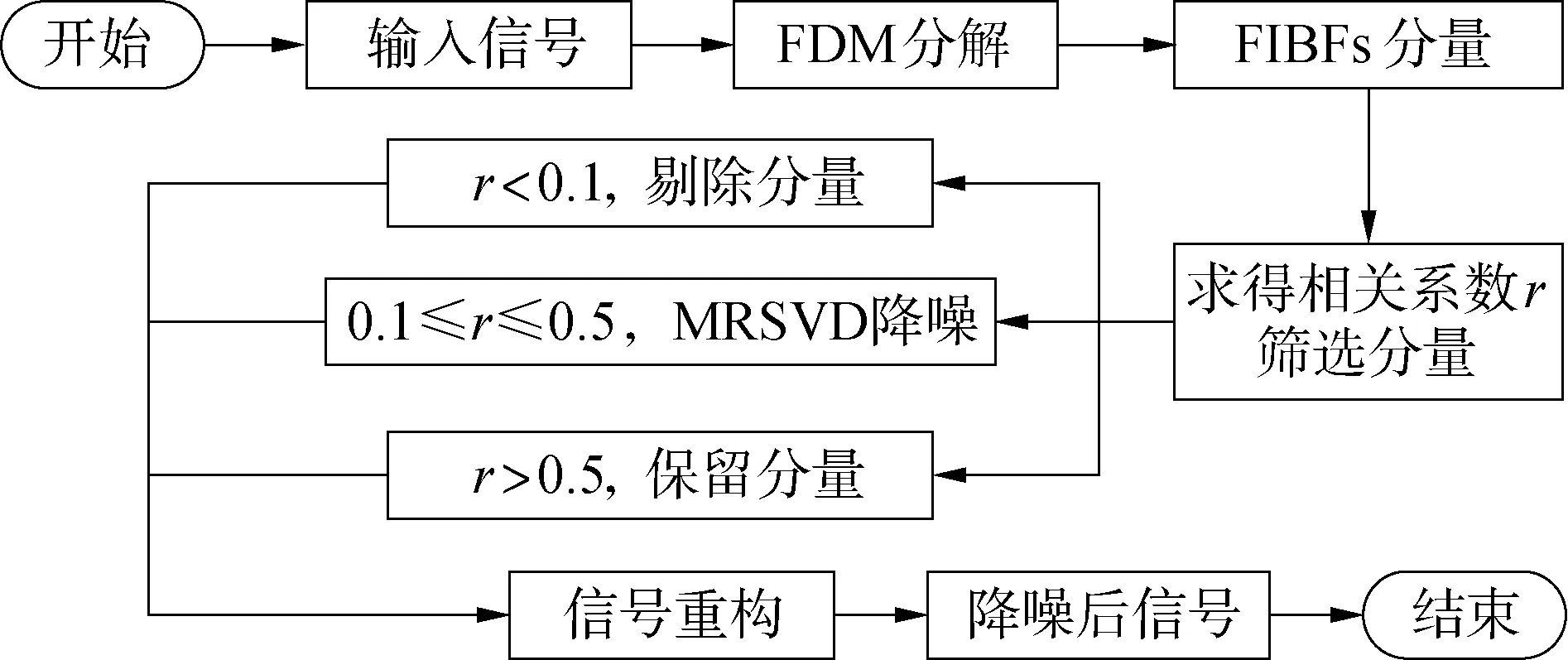
图2 FDM-MRSVD降噪流程Fig.2 Flowchart of FDM-MRSVD denoising

1)采用FDM方法对原始信号进行处理,分解为多个FIBFs和1个残余分量;

2)应用相关系数法筛选FIBFs分量。相关系数小于0.1的FIBFs分量中基本不包含正常信号,予以剔除;相关系数大于0.5的FIBFs分量中包含大量正常信号,予以保留;相关系数在0.1～0.5的FIBFs分量同时包含部分正常信号和噪声信号,重构后采用MRSVD方法降噪;

3)将MRSVD降噪后FIBFs分量和相关系数大于0.5 FIBFs分量进行重构,得到最终降噪后信号。

1.4 相空间重构

对离散时间信号z(i)重构相空间为:

(7)

式中:Z为重构之后的相空间;τ为延迟时间;m为嵌入维数;n=N-(m-1)τ;l=1,2,…,N。

在相空间重构中,延迟时间τ及嵌入维数m的选择非常关键。最佳延迟时间τ0、最佳嵌入维数m0常分别采用互信息法和虚假最近邻点法确定[15]。

1.5 混沌图像特征提取方法

对于不同的混沌系统,具有混沌特性的信号都会生成独特且明显特征的混沌吸引子重构相轨迹图(简称相图)及Poincaré截面图。相轨迹图的扩张和收缩趋势可以反映系统的混沌状态[16]。Poincaré截面图上截点分布扩张和收缩趋势可以反映系统的混沌状态[17]。获得相图及Poincaré截面图的步骤为:

1)采用互信息法和虚假最近邻点法确定重构相空间的参数τ0和m0;

2)对离散时间信号按式(7)进行相空间重构,将该信号重构为m0维相空间;

3)在相空间内选取任意分量及其相邻的2个分量,即可得到三维相图;

4)在相空间内,选取1个截面与轨迹线相交,该截面不与轨迹线相切并且不包含轨迹线,即可得到包含截点的Poincaré截面图。

2 试验信号降噪处理

2.1 水轮机空化AE信号采集

在处于国内领先水平、综合误差<±0.2%的闭式水轮机模型试验台上进行水轮机空化试验。选择导叶拐臂和转轮下环底部布置AE传感器,该位置距离发生空化部位较近且金属厚度较小,可以减少信号在传递过程中的能量损失和设备噪声的影响。在试验过程中,采用声发射信号采集系统采集各个测点的声发射信号。

2.2 FDM-MRSVD降噪分析

从导叶拐臂处AE传感器采集到的临界空化状态数据中截取长度为4 096的水轮机空化AE信号数据,信号波形图及频谱图如图3所示。

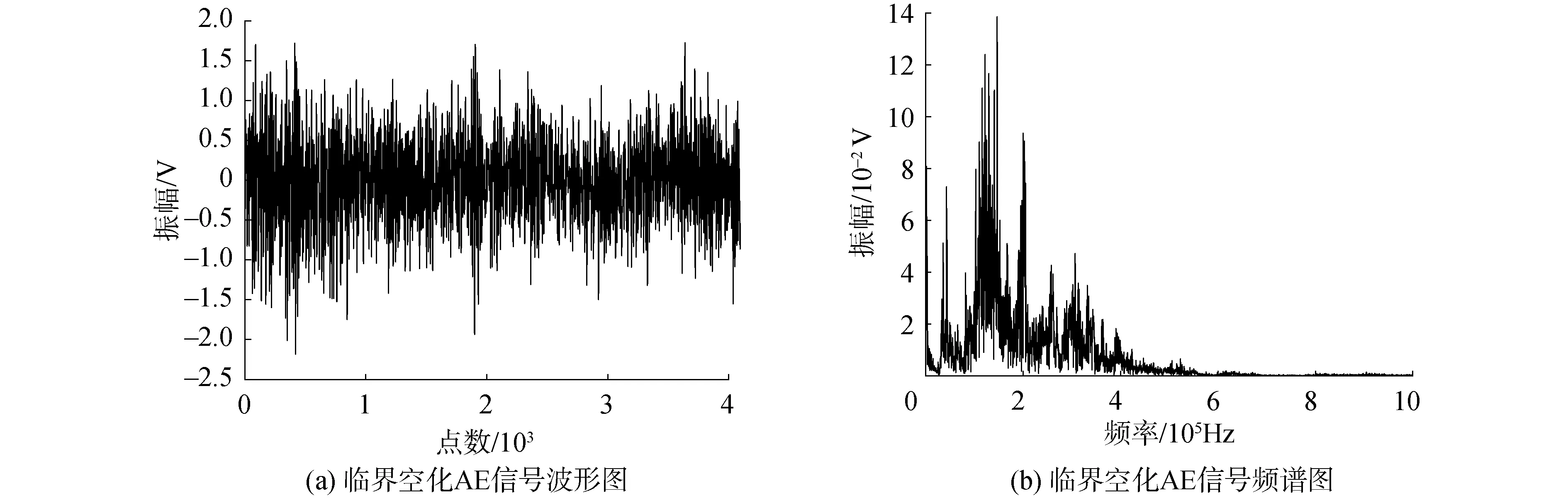
图3 临界空化AE信号Fig.3 Critical cavitation AE signal

对临界空化原始信号进行FDM处理,得到28个FIBFs和1个残余分量。因篇幅限制,仅展示8个典型的FIBFs的波形图(见图4)。可以发现,信号被有效分解,而且避免了模态混叠现象。计算分解得到的所有FIBFs的相关系数,部分分量的相关系数见表1。

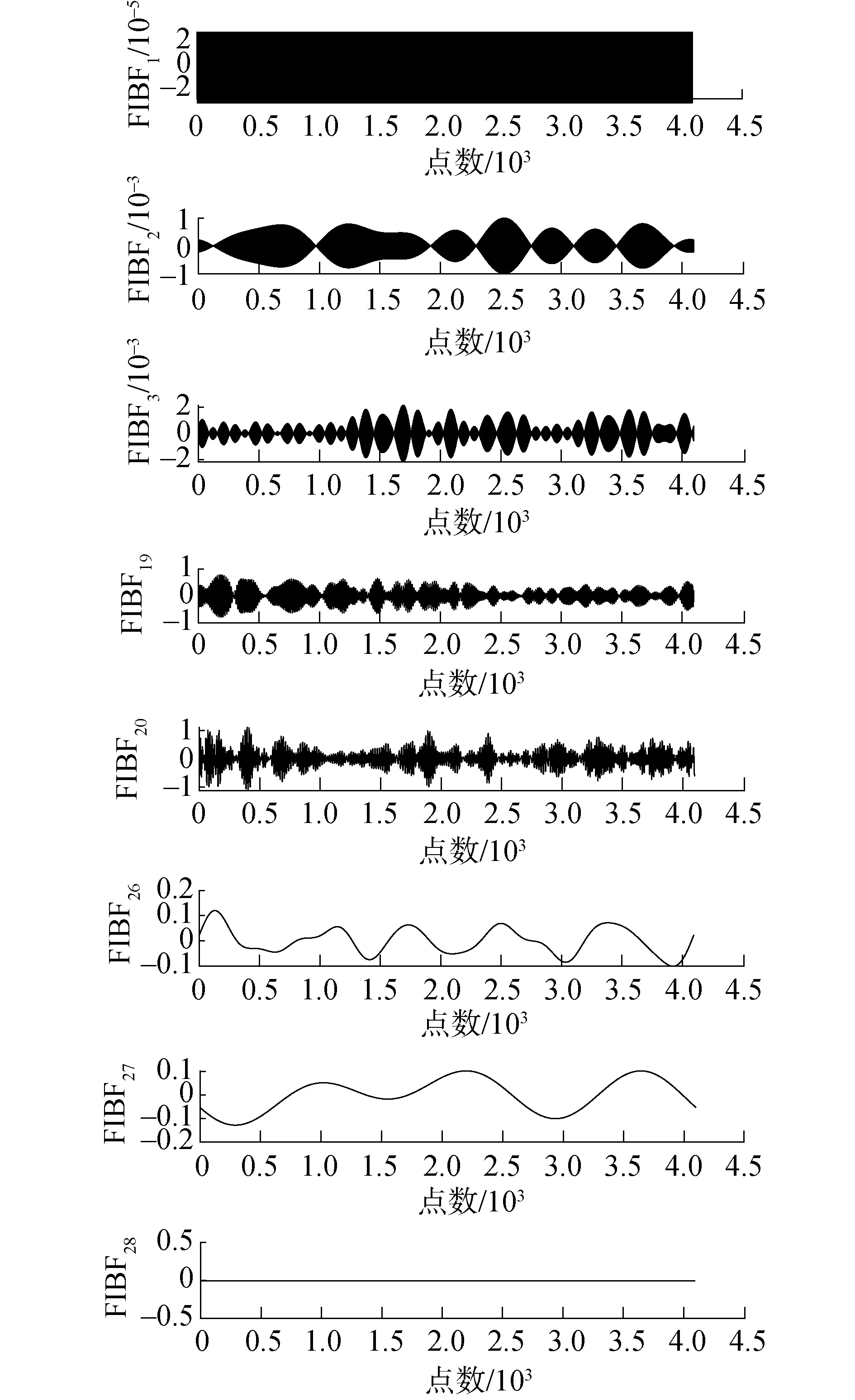
图4 FDM处理结果Fig.4 Results of FDM

FIBF1～FIBF13、FIBF23～FIBF28相关系数小于0.1,予以剔除。FIBF20相关系数大于0.5,予以保留。FIBF14～FIBF19、FIBF21、FIBF22相关系数大于0.1且小于0.5,进行重构后进行MRSVD降噪。将MRSVD降噪后的分量与保留的分量FIBF20进行重构,得到降噪处理后的信号。为评价FDM-MRSVD方法的降噪效果,再分别采用FDM降噪方法和MRSVD降噪方法对临界空化AE原始信号进行降噪处理,降噪处理后的信号波形如图5所示。

图5 降噪处理后水轮机空化AE信号波形图Fig.5 Turbine cavitation acoustic emission signals oscillogram denoised by three methods

由图5可知,3种方法降噪后的波形图均保持了原始信号的轮廓,3种方法都能有效地降低水轮机空化AE信号的噪声。FDM-MRSVD降噪方法所得水轮机空化AE信号波形图相比较而言最平滑。为进一步比较3种方法的降噪效果,降噪后信号分别进行FFT处理,得到频谱图见图6。

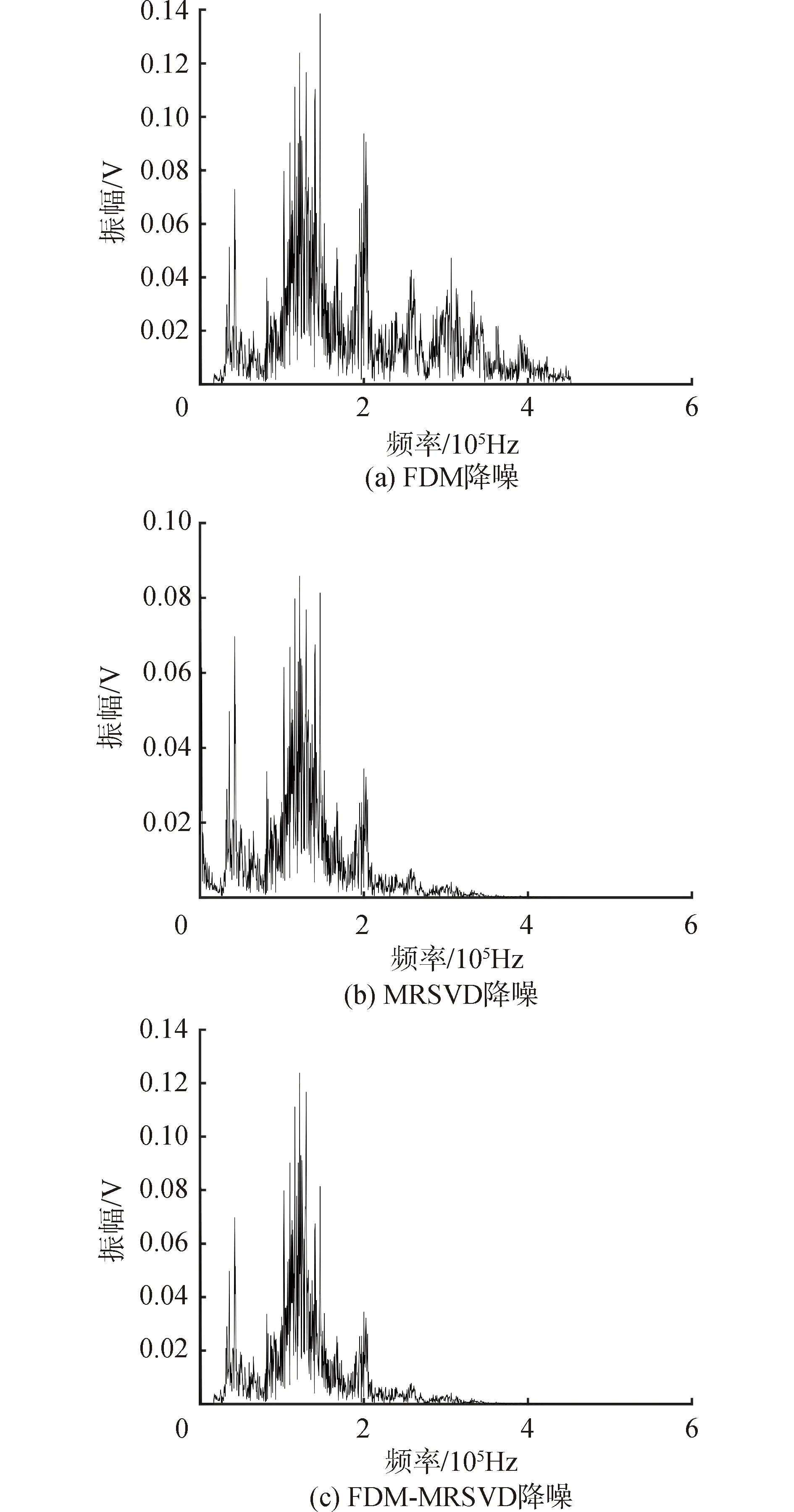
图6 降噪处理后水轮机空化AE信号频谱Fig.6 Turbine cavitation acoustic emission signals frequency spectrogram denoised by three methods

图6(a)中200 kHz以上信号频段仍有大量噪声残留,说明仅使用FDM方法虽然可以对信号完备分解,但仍有些分量同时包含正常信号和噪声信号,降噪效果并不理想。从图6(b)中可以看出,200 kHz以上的信号频段的噪声基本被消除,但是信号整体幅值相较原始信号幅值下降很多,说明仅使用MRSVD方法造成了较多的能量损失。而图6(c)中经过降噪后信号主要集中分布于200 kHz以下,试验信号中的噪声被剔除,细节特征得到了较大程度的保留。

3 空化AE信号的混沌图像特征提取

本文分别从导叶拐臂处AE传感器采集到的无空化、空化初生和临界空化3种状态数据中截取长度为4 096的水轮机空化AE信号数据组成样本序列。先采用FDM-MRSVD方法对3个不同空化状态的信号进行降噪,再通过互信息法和虚假最近邻点法计算样本序列的相空间重构参数τ0和m0,结果见表2。

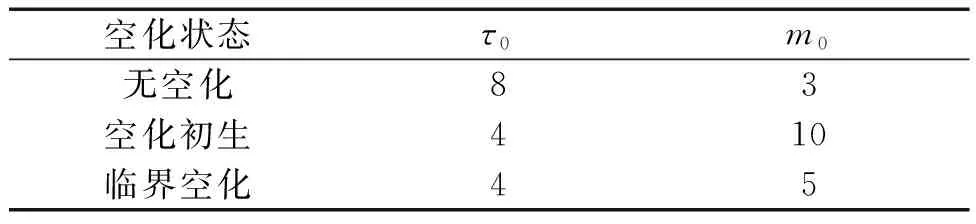
表2 不同空化状态AE信号相空间重构参数Table 2 Phase space reconstruction parameters of AE signals in different cavitation states

3.1 相图分析

分别对3种不同空化状态的AE信号进行相空间重构,选取每个相空间内前3个相邻分量画出三维相图,如图7所示。

图7 不同空化状态AE信号相图Fig.7 AE signal phase diagrams in different cavitation States

根据空化相关理论,当过流部件的真空压力逐渐降低后,水轮机流道内水流的流态就开始变得复杂。并且随着压力逐渐降到低于饱和汽化压力,流体内开始出现大量空泡。由于空泡的出现,会造成部分流道的阻塞,导致流体的连续性和稳定性受到破坏。产生的大量空泡会伴随流体流动,流到高于压力临界值的区域会发生溃灭。大量空泡溃灭会在短时间产生巨大冲击,这些微型射流导致水流流态的紊乱程度剧增,产生的声发射信号混沌程度大幅度增加。图7的变化可以直观体现空化演变过程。从图7可以看出无空化AE信号、初生空化AE信号及临界空化AE信号经重构后有完全不同的重构相图。在同一标度下的相图,具有完全不同的大小,形状,稀疏程度。随着空化系数的减小,空化愈剧烈,相轨迹图的扩张趋势愈明显。这说明重构相图可以很好地表征不同空化状态,可以作为反映水轮机空化状态的一种特征。

3.2 Poincaré截面图分析

在上述重构相空间中选取1个不与轨迹线相切且不包含轨迹线的截面与轨迹线相交,画出无空化、初生空化及临界空化状态下AE信号的Poincaré截面图,如图8所示。

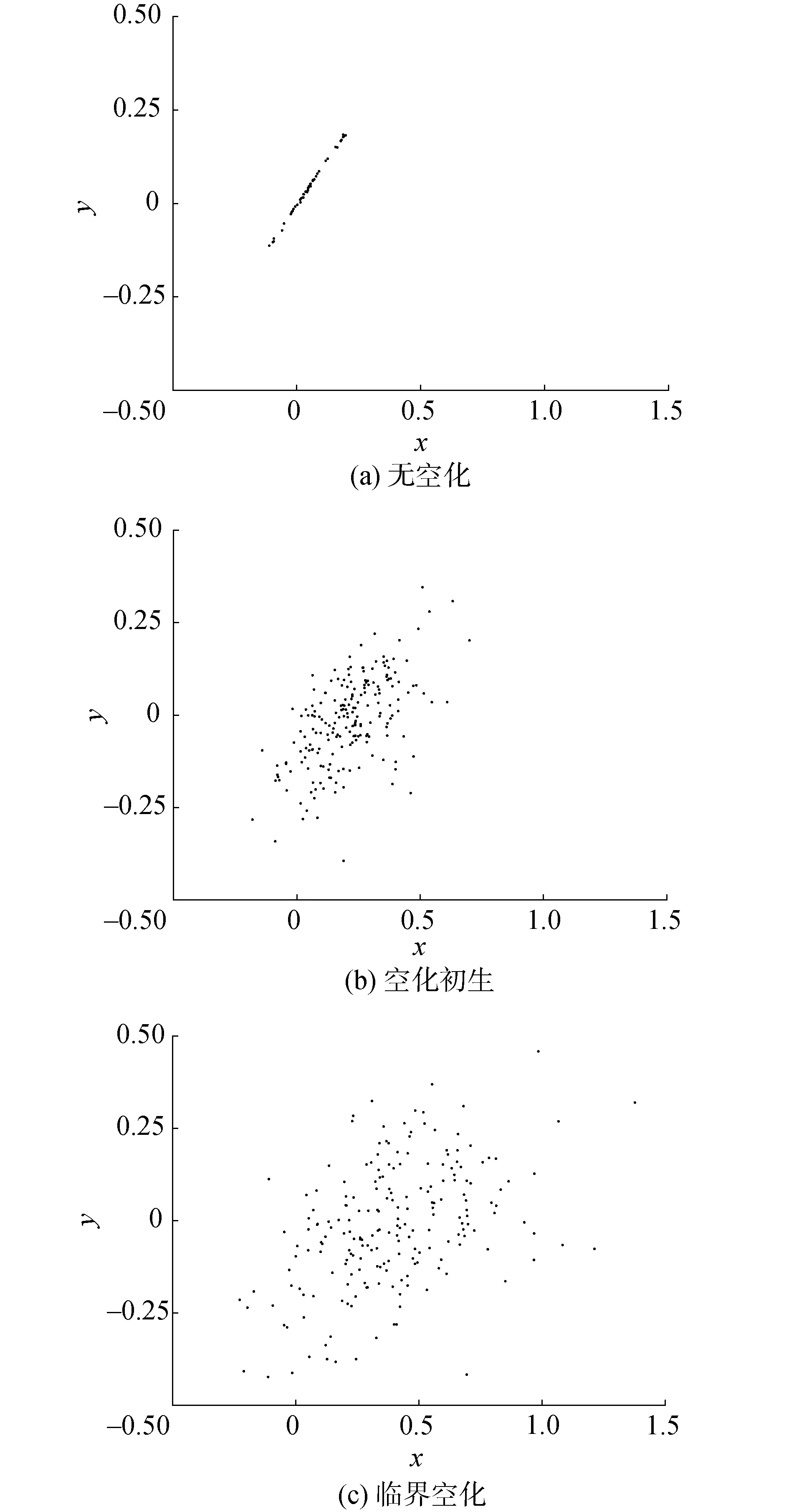
图8 不同空化状态AE信号Poincaré截面Fig.8 Poincaré cross-section of AE signals in different cavitation states

由图8(a)可知,水轮机内尚未发生空化,Poincaré截面图上截点分布集中在一条直线上,证明水轮机内部流动混乱程度较小。图8(b)和图8(c)中,Poincaré截面图上截点分布呈片状分布,且分散加剧,具有明显的混沌特征。在无空化、空化初生及临界空化3种不同的状态下,Poincaré截面图上截点的分布及稀疏程度存在明显差异。随着空化系数的减小,空化愈加严重,Poincaré截面图上截点的分布愈加分散。因此,Poincaré截面图也可作为反映水轮机空化状态的一种特征。