不同气候条件下几种对流层模型性能分析

戴 祺，章浙涛，文援兰，曾 平，王苗苗

不同气候条件下几种对流层模型性能分析

戴 祺1，章浙涛1，文援兰1，曾 平1，王苗苗2

（1. 河海大学 地球科学与工程学院，南京 211100；2. 常州工学院 计算机信息工程学院，江苏 常州 213032）

对流层延迟是全球卫星导航系统（GNSS）高精度定位测量的重要误差源之一。鉴于对不同气候条件下对流层模型性能分析不足，针对高压低温低湿、低压高温高湿气候条件，通过相对动态定位实验来比较萨斯塔莫宁（Saastamoinen）、改进霍普菲尔德（M-Hopfield）、新布伦瑞克三代（UNB3）这三种对流层模型精度并分析其适用性能。实验结果表明：低压高温高湿环境下，坐标偏差序列波动相对剧烈且在垂直方向上多峰值，各模型坐标解算精度相对更低且模型间精度差异更大，UNB3模型整体改正效果更好。高压低温低湿环境下，Saastamoinen模型更为适用，在垂直方向上表现显著，M-Hopfield模型次之。气象因子（气压、气温、相对湿度）影响对流层延迟量且气压影响程度相对低于气温与相对湿度。高压低温低湿环境下模糊度固定率高出约15 %，UNB3模型定位的模糊度固定率高于Saastamoinen与M-Hopfield模型，且后两种模型的模糊度固定率相差不大。

全球卫星导航系统（GNSS）；相对动态定位；对流层修正模型；气候条件

0 引言

在全球卫星导航系统（global navigation satellite system，GNSS）定位测量中，卫星发射信号在穿过距地面50 km以下的中性大气层时，其传播速度、路径因受大气效应影响，易导致卫星信号发生折射与弯曲，产生对流层延迟[1]。对流层延迟受大气折射率影响，且大气折射率与传播路径上的气温、气压、相对湿度高度相关。文献[2]指出，因对流层大气对于GNSS卫星发射的电磁波信号而言为非色散介质，使该延迟与信号频率无关，难以像处理电离层一般通过观测值组合对其进行削弱甚至消除，这使其成为GNSS高精度定位测量重要误差源之一。随着GNSS系统建设日益完善，涵盖定位、导航与授时等功能的定位测量技术在高精度大地测量与控制测量、精确制导武器、无线电空间大地测量等精密定位领域发挥着难以替代的作用。文献[3]指出，为满足各类用户对导航定位严苛的精度要求，准确估计并有效改正对流层延迟已成为亟待解决的问题。

国内外众多学者在对流层延迟方面开展了深入研究，大量延迟修正方法被提出，如文献[4-6]提及的模型改正法、参数估计法、求差法、外部修正法，这些方法在导航定位中已取得了成效。其中，常用对流层延迟修正模型有基于实测气象数据的气象模型，如文献[7-10]提及的萨斯塔莫宁（Saastamoinen）模型、霍普菲尔德（Hopfield）模型、勃兰克（Black）模型等；不依赖实测气象数据的纯经验模型，如文献[11-15]提及的欧洲地球静止导航覆盖系统（European geostationary navigation overlay service，EGNOS）模型、新布伦瑞克三代（University of New Brunswick 3，UNB3）模型、全球气温气压（global pressure and temperature，GPT）系列模型等。合理选取映射函数有利于精确获取传播路径上的对流层延迟，常见映射函数如文献[16-18]提及的尼尔映射函数（Niell mapping function，NMF）、全球映射函数（global mapping function，GMF）、维也纳一代映射函数（Vienna mapping function 1，VMF1）等。模型改正法是在解得天顶对流层延迟（zenith tropospheric delay，ZTD）后通过映射函数[19]将其投影至传播路径方向上以获取斜对流层延迟；因其在常规观测环境、气候等条件下改正效果好，且能够有效避免方程秩亏[20]、计算简易而得到广泛应用。

我国地域辽阔、南北跨度大，地势西高东低，地形多样，海陆热力差异凸显等特点致使气候复杂多变、大陆性季风气候显著，间接造成“地区局部气候”现象。气候变化导致对流层中水汽、温度与气压值随之变化，从而影响卫星信号在对流层中传播而产生延迟。目前，针对对流层延迟的研究虽有涉及气候因素，但大多数仅聚焦于如文献[21-28]所提出的针对不同程度雨雪天、暴雨天气条件、两极地区极端条件与不同高度角、高程等环境下的对流层模型性能分析，而鲜有对不同气候特征存在显著差异时的对流层模型适用性分析。对于国内GNSS导航定位用户而言，合理选取现有或构建新型对流层模型以适用于所处区域的高精度定位，满足实际需求是目前应聚焦的重心。本文分析香港地区不同气候条件下对流层模型（包括Saastamoinen、M-Hopfield、UNB3模型）的性能，旨在为高精度导航定位时合理选取对流层模型提供参考。

1 对流层修正模型

1.1 Saastamoinen模型

Saastamoinen模型计算公式为

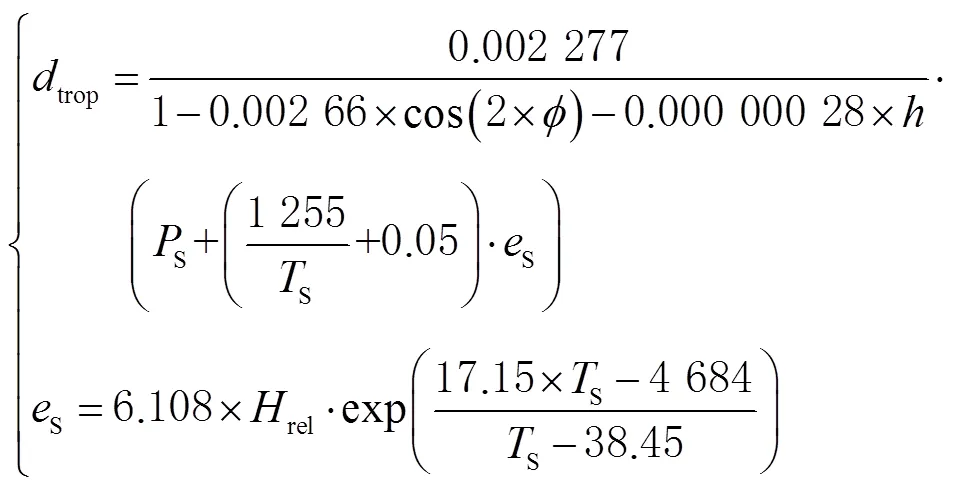
1.2 M-Hopfield模型

M-Hopfield模型计算公式为

1.3 UNB3模型

UNB3模型计算公式为

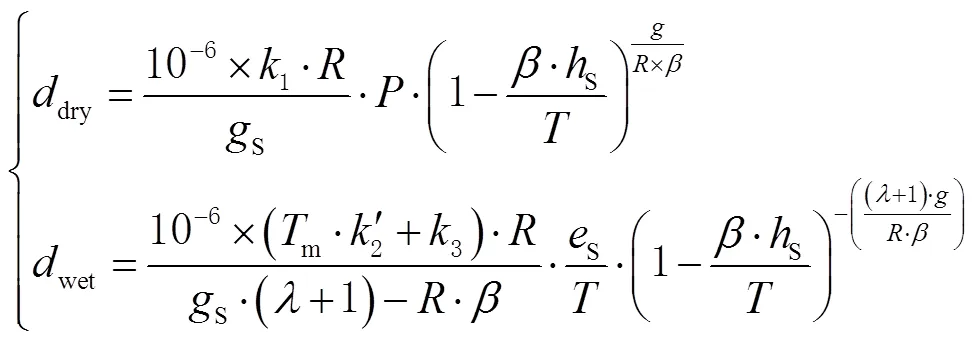
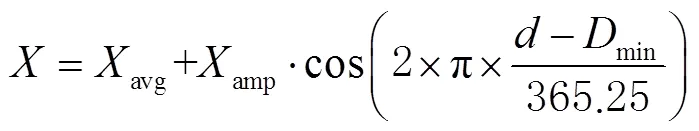
文献[30]指出：UNB3模型充分考虑气象参数季节性变化特征，采用尼尔（Niell）思想将海平面上某处气象元素看作是纬度与年积日的余弦函数，如式（5）所示，基于构建的查找表，可根据测站纬度、年积日直接查找求得该测站气象参数；然后将求得的气象参数代入式（3），由UNB3模型计算测站高程处的天顶对流层延迟。

2 数据来源及参数配置

2.1 数据来源

本文实验数据源于香港卫星定位参考站网中相距约为49.89 km的昂坪（HKNP）站与黄石（HKWS）站。其中，基准站、流动站分别为HKNP、HKWS，天台参考站之一的T430站命名方式不同于其他17个测站，没有带“HK”标识，该参考站设备包括接收机（Leica GR50）和天线（Trimble 59800.00+SCIT），T430可替代HKFN进行服务。测站分布如图1所示。

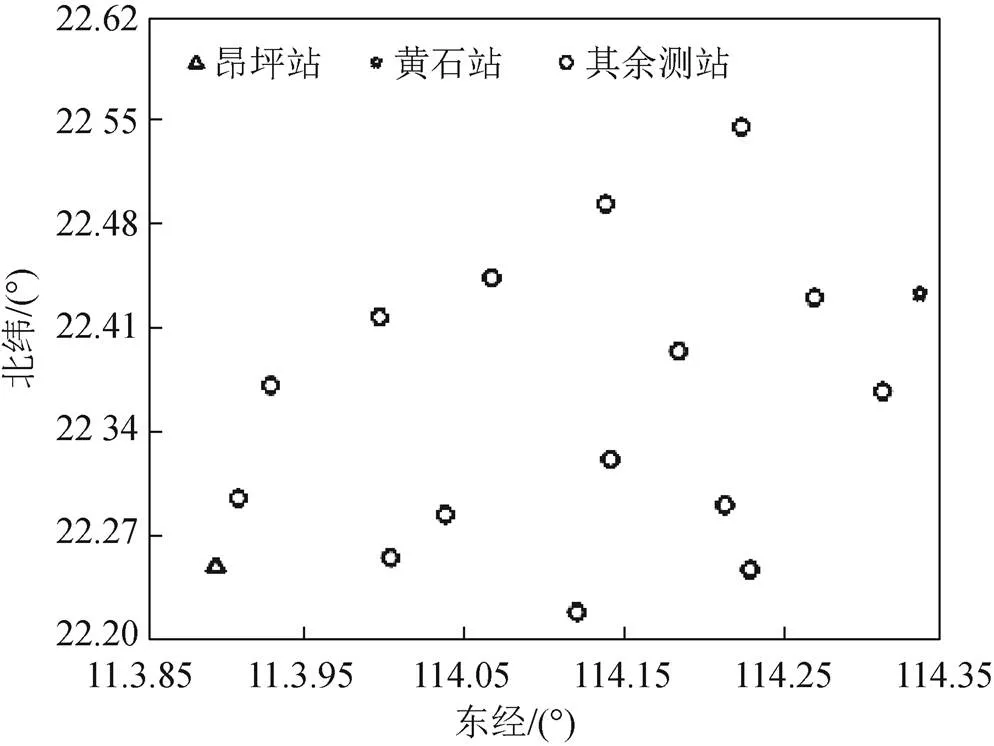
图1 香港地区连续运行参考站分布

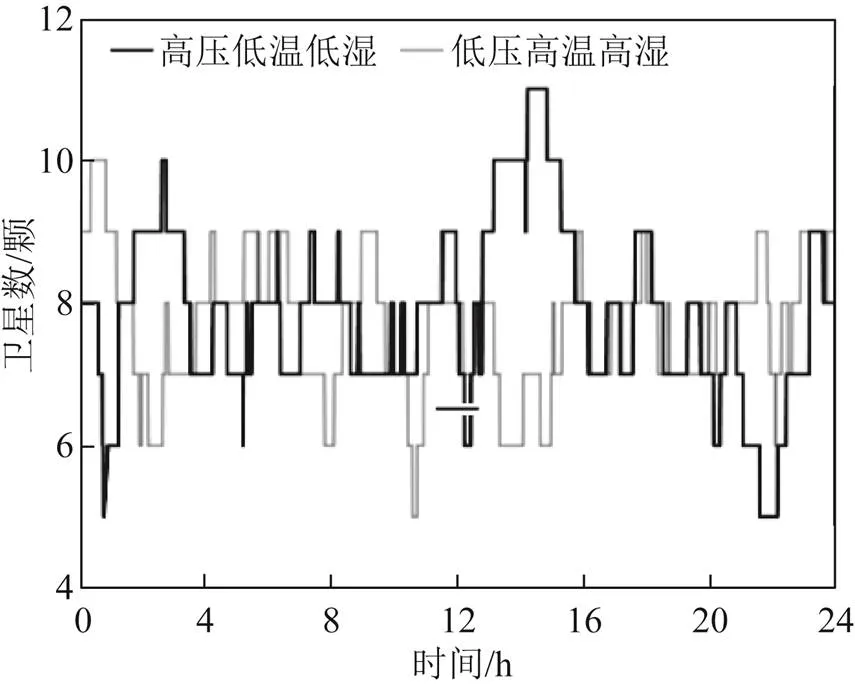
图2 不同气候条件下BDS+GPS系统日平均可见卫星数分布序列

香港地区属亚热带季风气候，夏季炎热潮湿、冬季凉爽干燥，该气候特征可满足对流层模型性能分析需求。但因各季气象因子日变化错综复杂，采用连续获取测站数据的手段往往不能突出季节特征，因而选取测站在能够凸显气候特征差异下的2021-01-01、01-02、01-08—01-12高压低温低湿条件下与2021-06-21、07-07、07-18、07-23—07-25、07-27低压高温高湿条件下共14 d的混合观测数据、导航与气象数据，采样间隔为30 s。

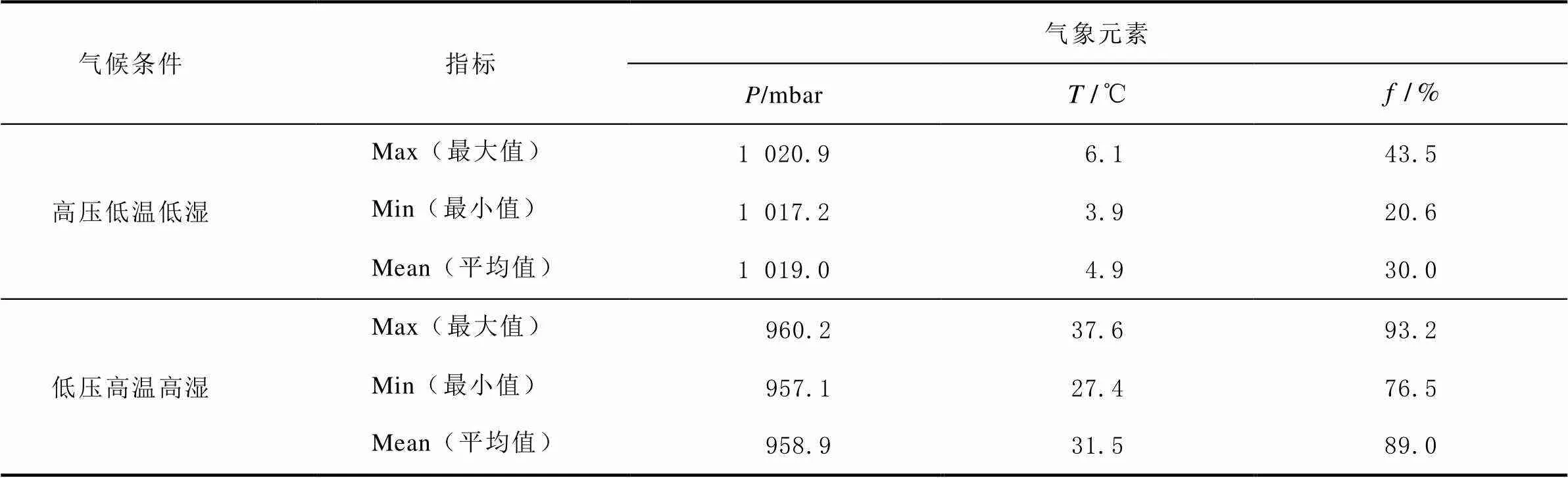
表1 不同气候条件下测站数据气象元素值统计

2.2 模型基本信息及参数配置

表2 对流层模型基本信息

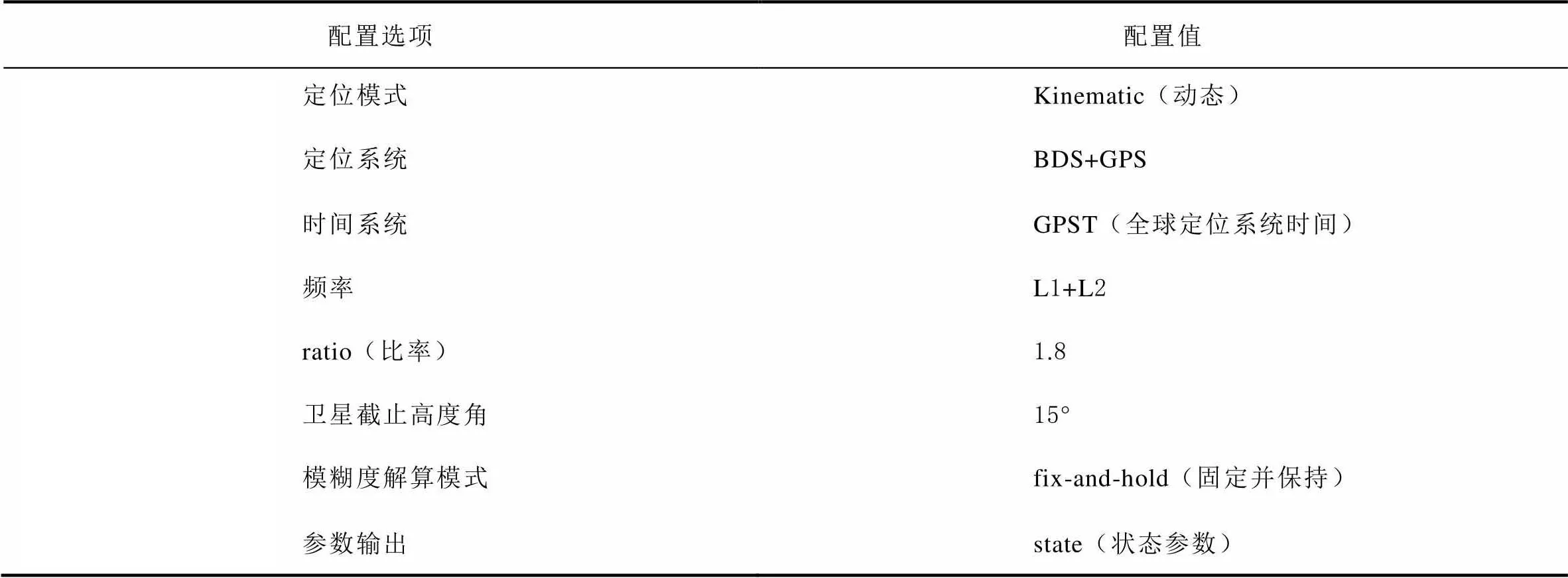
表3 配置文件关键参数值

2.3 精度评定指标

选取平均偏差和均方根作为精度指标。平均偏差是指待处理数据中各数值与参考值离差绝对值的算术平均数；均方根是指待处理数据中各数值与参考值离差平方和的算术平均数的二次根。平均偏差、均方根计算公式分别为：

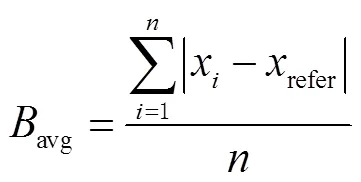
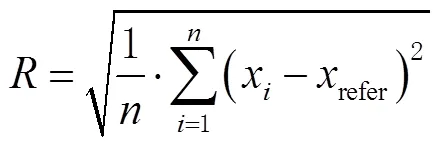
3 实验与结果分析

3.1 不同气候条件下定位结果精度分析

选取2021-01-01、01-02、01-08—01-12共7 d数据作为高压低温低湿环境下相对动态定位实验的数据。如图3所示为2021-01-01，即年积日（day of year，DOY）为001时使用Saastamoinen、M-Hopfield和UNB3模型解算测站浮点解在站心坐标系下E、N、U方向上的坐标偏差时间序列分布。由图可知，该气候条件下，Saastamoinen、M-Hopfield和UNB3模型解算的坐标偏差序列分布规律大体相似。结合偏差序列纵坐标取值范围来看可以发现，模型偏差值在E、N方向上变化平稳，其偏差最大、最小值之差分别在0.5514、0.4745 m以内；而U方向上波动相对较大，其偏差最大、最小值之差分别在0.7485 m以内。3种模型偏差序列在4～12 h之间波动表现较为明显，18 h后趋于稳定。因测站当天处于低温低湿条件下而导致对流层延迟量较小，模型间改正效果差异不大，使各模型测站坐标解算偏差降低，偏差序列波动减缓。

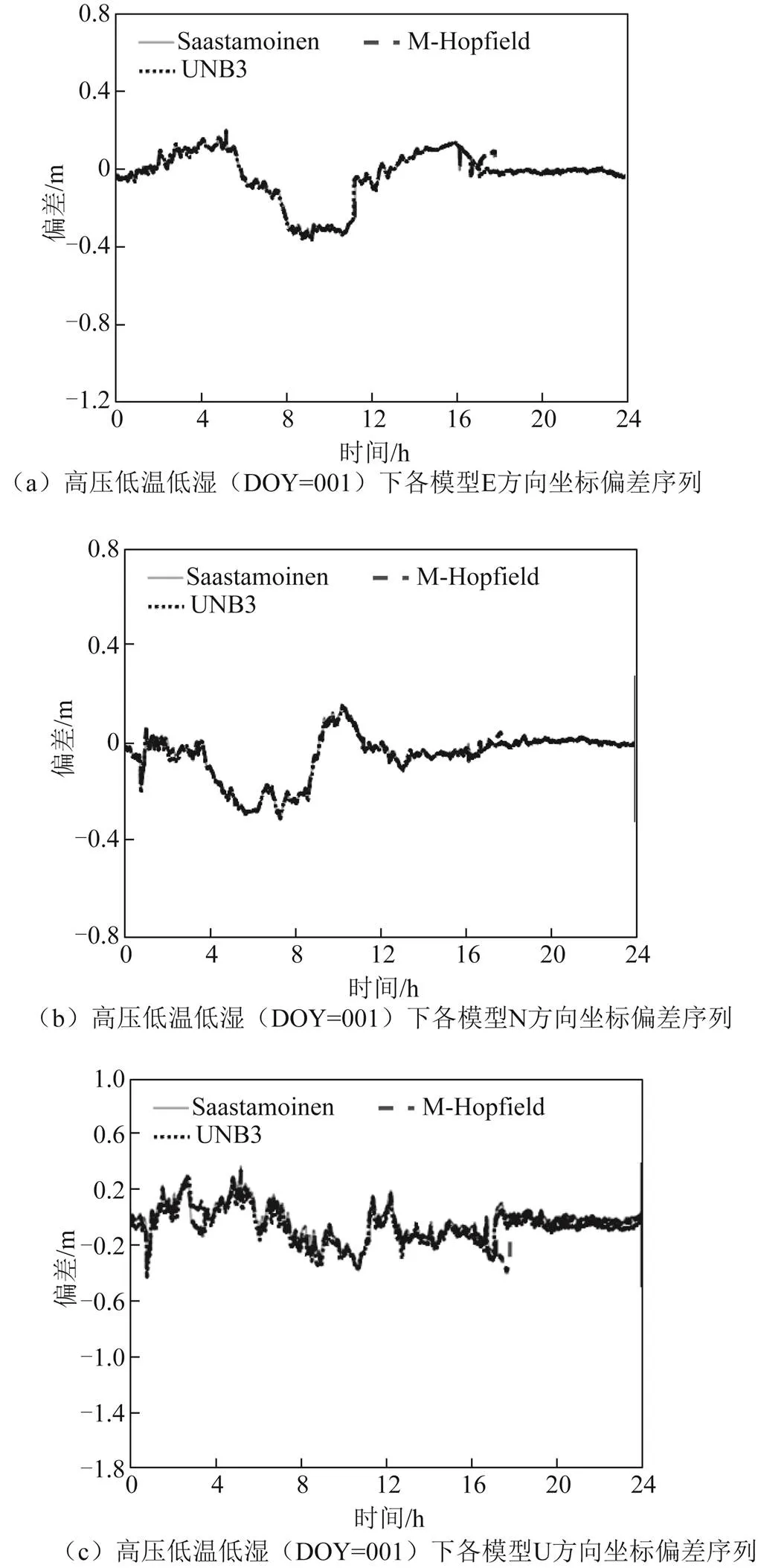
图3 高压低温低湿（DOY=001）下各模型ENU向坐标偏差序列

选取2021-06-21、07-07、07-18、07-23—07-25、07-27共7 d数据作为低压高温高湿条件下相对动态定位实验数据。如图4所示为2021-07-18，即DOY为199时使用3种模型解算测站浮点解在站心坐标系下E、N、U方向上的坐标偏差时间序列分布。由图可知，该气候条件下，Saastamoinen、M-Hopfield和UNB3模型解算的坐标偏差序列分布规律大体接近。结合偏差序列纵坐标取值范围可以发现，模型偏差值在E、N方向上变化平稳，其偏差最大、最小值之差分别在1.2488、0.6297 m以内；而U方向上波动相对较大，其偏差最大、最小值之差分别在2.0145 m以内。3种模型偏差序列于10～13 h之间在E、N、U方向上均产生明显波动，20 h后趋于稳定。因测站当天处于高温高湿条件下导致延迟量较大，增大模型间改正效果差异，可使各模型坐标解算精度表现差异更为显著。

图4 低压高温高湿（DOY=199）下各模型ENU向坐标偏差序列

如表4所示为2021年不同气候条件下各模型坐标解算平均偏差与均方根的日均值统计结果。如表5所示为2021年不同气候条件下各模型在DOY为001与199的坐标解算平均偏差、均方根统计结果。由表4、表5统计结果可知，高压低温低湿环境下各对流层模型坐标解算精度相对更高，尤其在U方向表现显著。DOY为001与199的定位结果与日均值在精度表现上大体一致，即在高压低温低湿气候条件下，Saastamoinen、M-Hopfield模型精度表现总体上优于UNB3模型，尤其在U方向更为显著；在低压高温高湿气候条件下，UNB3模型整体表现效果较好。其中，根据表5的定位结果平均偏差，Saastamoinen、M-Hopfield、UNB3模型在高压低温低湿环境下的3D坐标解算精度相对于低压高温高湿环境下分别提高了168.4 mm（53.0 %）、153.7 mm（48.9 %）、117.6 mm（41.4 %）；从定位结果均方根来看，Saastamoinen、M-Hopfield、UNB3模型在高压低温低湿环境下的3D坐标解算精度相对于低压高温高湿环境下分别提高了239.7 mm（52.7 %）、230.1 mm（50.5 %）、209.4 mm（47.9 %）。

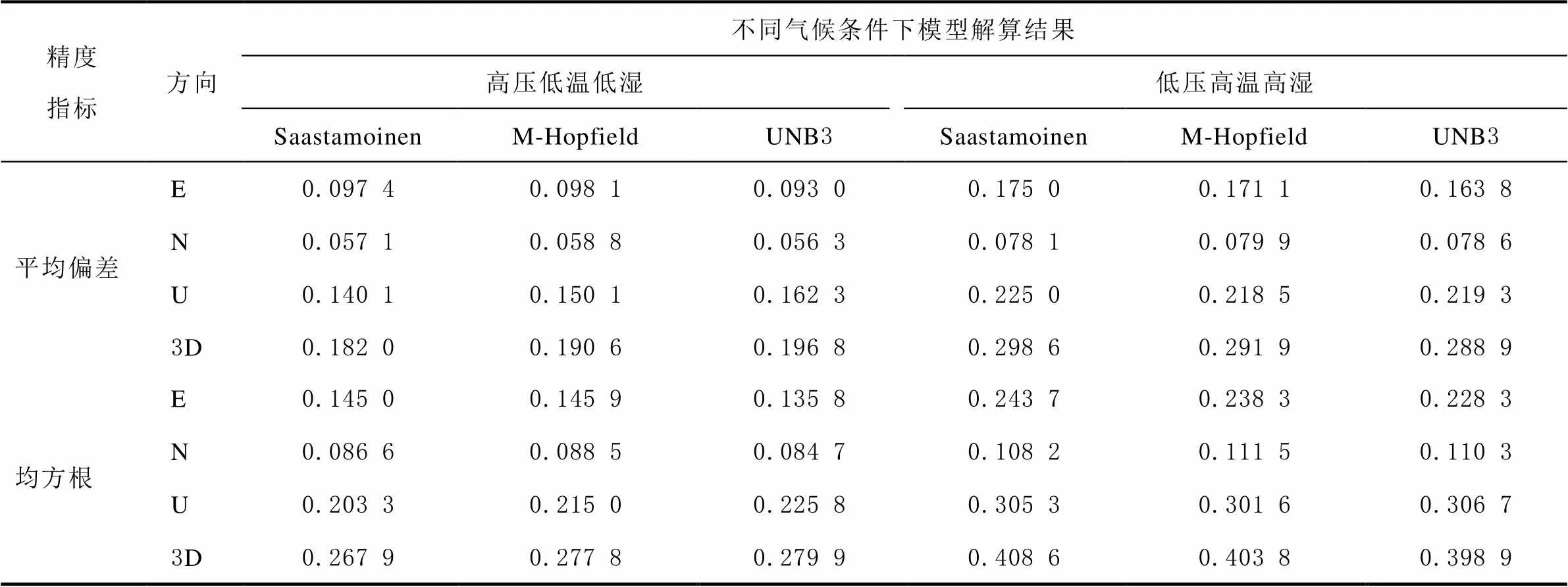
表4 不同气候条件下各模型定位结果精度日均值统计 m

表5 不同气候条件（DOY=001&199）下各模型定位结果精度统计 m

高压低温低湿环境下，3种对流层模型的坐标解算精度在E、N方向上差异不大，U方向上差异显著。从定位结果平均偏差来看，Saastamoinen、M-Hopfield模型较UNB3模型的坐标解算精度在U方向上分别提高了23.4 mm（20.2 %）、7.8 mm（6.7 %），在3D方向上分别提高了17.2 mm（10.3 %）、5.9 mm（3.5 %）；从定位结果均方根来看，Saastamoinen、M-Hopfield模型较UNB3模型的坐标解算精度在U方向上分别提高了18.6 mm（13.0 %）、1.5 mm（1.1 %），在3D方向上分别提高了12.4 mm（4.5 %）、2.0 mm（0.9 %）。由此得出，高压低温低湿环境下，Saastamoinen、M-Hopfield模型较UNB3模型更为适用，其中以Saastamoinen模型表现最优。

低压高温高湿环境下，3种对流层模型的坐标解算精度在E、N方向上差异较大，U方向上差异相对较小些。从定位结果平均偏差来看，UNB3模型较Saastamoinen、M-Hopfield模型的坐标解算精度在U方向上分别提高了18.8 mm（7.6 %）、16.1 mm（6.6 %），在3D方向上分别提高了33.6 mm（10.6 %）、30.2 mm（9.6 %）；从定位结果均方根来看，UNB3模型较Saastamoinen、M-Hopfield模型的坐标解算精度在U方向上分别提高了1.5 mm（0.4 %）、5.3 mm（1.6 %），在3D方向上分别提高了17.9 mm（4.0 %）、18.7 mm（4.1 %）。由此得出，低压高温高湿环境下，UNB3模型较Saastamoinen、M-Hopfield模型更为适用，且在3D方向上坐标解算精度有明显提高。

3.2 不同气候条件下各模型天顶对流层延迟时间序列分析

如图5所示为2021-01-01，各对流层模型解算黄石（HKWS）站的ZTD值及气象因子（气压、气温、比湿）时间序列。由图可知，在0～16 h之间，各模型解算黄石站的ZTD值序列发生明显波动：在0～4 h之间波动最为剧烈，ZTD值之差高达1.6059 m；16 h后序列趋于平稳。从气象因子时间序列来看，在ZTD值波动时间范围内，气压值下降约2 mbar，气温值升高约8℃，比湿值下降约15％。测站当日处于高压低温低湿环境下，气象因子在短时间内的变化会影响对流层模型延迟量及修正。可见，当日气象因子的变化在一定程度上反映出Saastamoinen、M-Hopfield、UNB3模型解算测站ZTD值序列的大致变化，即ZTD值随各气象因子的变化而发生波动，随后，气象因子变化趋于稳定，ZTD值波动也逐渐平缓。此外，各模型间差异较小，尤以Saastamoinen与M-Hopfield模型间最为接近。

图5 高压低温低湿环境下各模型ZTD值及气象因子时间序列

如图6所示为2021-07-08，各对流层模型解算黄石（HKWS）站的ZTD值及气象因子（气压、气温、比湿）时间序列。由图可知，各模型解算黄石站的ZTD值序列发生连续性波动，1～4 h之间波动幅度相对较大，ZTD序列极大、极小值之差约为0.6 m。从气象因子时间序列来看，在ZTD值波动时间范围内，气压、气温、相对湿度值发生明显持续变化，在ZTD值波动幅度较大时间范围内，除气压值变化平稳外，气温、相对湿度值分别有明显上升、下降，变化范围分别约为4℃、18％以内。测站当日处于低压高温高湿的环境下，气象因子始终保持在高值状态，且全天内发生持续变化，以相对湿度最为显著，这会极大影响对流层延迟量及其模型修正。可见，当日气象因子的变化在一定程度上反映出Saastamoinen、M-Hopfield、UNB3模型解算测站ZTD值序列的大致变化，即ZTD值随各气象因子的不断变化而发生持续性波动。此外，Saastamoinen与M-Hopfield模型间差异较不明显，但二者与UNB3模型的ZTD值差异相对明显。

图6 低压高温高湿环境下各模型ZTD值及气象因子时间序列

总之，不论在何种气候条件下，各对流层模型解算的测站ZTD值大小会受测站处气象因子影响，且温度、相对湿度对其影响程度相对更大。因ZTD中的干延迟部分基于气象参数建模进行改正；而湿延迟部分因受比湿影响显著，且难以通过建模来修正。加之香港地区夏季气压低、气温高，同时因受亚热带季风气候影响，常出现降雨、台风而造成大气湿度高，该气候条件下对流层延迟量较大，进而使各实验对流层模型间的坐标解算精度差异表现明显，其中以UNB3模型表现最优；而冬季气压高、气温低，因降水量少、气候干燥等导致大气湿度低，该气候条件下对流层延迟量较小，进而使各模型间的坐标解算精度整体提高且模型间差异不大，其中以Saastamoinen模型表现最优，M-Hopfield模型次之。

3.3 不同气候条件下浮点解、固定解精度统计分析

如图7所示为冬、夏季中DOY为001与199时不同对流层模型于不同固定率下E、N、U方向上坐标解算的均方根统计结果。由图可知，基于浮点解的定位结果精度为分米级。高压低温低湿气候条件下，各模型在E、N、U方向上坐标解算精度的均方根低于1.5 dm，由表5可知，3D方向模型间的精度差异在12.4 mm以内；低压高温高湿气候条件下，各模型在E、N、U方向上坐标解算精度的均方根低于3.4 dm，且U方向的精度显著低于E、N方向，3D方向模型间的精度差异在18.7 mm以内。

图7 冬夏季各模型在不同固定率下均方根统计

如表6所示为不同气候条件下各模型定位结果固定率统计结果。由表可知，冬、夏季固定率分别在40 %～50 %、30 %～40 %之间，呈现出“阶梯式”递减趋势。在不同气候条件下，由于气象因子变化导致卫星信号发生不同程度的时延、失锁等现象，进而影响模糊度固定率。应用3种模型修正对流层延迟，结果表明：高压低温低湿条件下模糊度固定率比低压高温高湿条件下约高15 %。因UNB3模型不依赖于实测气象数据，而是根据测站年积日、纬度直接获取其气象参数，这表明该模型受气象因子变化影响较Saastamoinen和M-Hopfield模型相对不显著，从而使得应用UNB3模型定位的模糊度固定率高于应用Saastamoinen和M-Hopfield模型定位的模糊度固定率，且后2种模型定位的模糊度固定率相差不大。

表6 不同气候条件下各模型定位结果固定率统计 %

为进一步确定固定率对定位精度的影响，本文基于固定解对定位结果进行精度评定分析。如图8所示为冬、夏季中DOY为001与199时各模型在固定解下E、N、U方向上坐标解算的均方根统计结果。由图可知，高压低温低湿环境下，E、N、U方向上坐标解算精度的均方根为厘米级，且E、N方向的精度高于U方向，3D方向各模型间的精度差异分别在18.7、13.5、5.2 mm；低压高温高湿环境下，E、N方向上坐标解算精度的均方根达到厘米级，U方向为分米级，3D方向模型的精度差异约为18.6、16.0、2.6 mm。可知，固定解较浮点解定位精度在整体上高出一个量级，且固定解下模型间的精度差异在3D方向上相差不大。

不同气候条件下的定位结果均含浮点解。现对浮点解成因作如下分析：如图2所示，在确定所有历元下都能接收到7～9颗卫星信号时，可排除卫星数不足的影响。初步判断可能是因信号在传播过程中受到气象因子（尤其是水汽）影响而使信号中断，发生失锁。若失锁时间过长，则模糊度须重新计算；加上实验选取测站间基线较长，使大气残差（对流层、电离层延迟残差）难以消除，致使模糊度固定受影响，从而使定位结果产生浮点解。从图7、图8来看，不同气候条件下，增加固定率可有效提高坐标解算精度，且使模型间的精度差异缩小。在实际定位过程中因受周围环境因素影响导致固定率达不到100%，因而，可通过考虑卫星信号、大气环境变化、测区环境干扰程度等因素来获取高质量数据以提高坐标解算固定率，整体提高坐标解算精度，降低模型间的精度差异。

综上，Saastamoinen、M-Hopfield模型依赖于实测气象数据且采用标准大气模型获取气象参数，使用该类模型时，需要给出测站气象参数，这导致其对观测当天气象要素值变化稳定性有较高要求。在气象参数变化较快且不稳定时，模型改正效果较差。又因Saastamoinen模型对对流层进行区间划分，分段计算大气温度，使结果相比于M-Hopfield模型更加准确；因而，在香港地区气象条件变化相对稳定的高压低温低湿气候条件下进行相对动态定位，选用Saastamoinen模型更佳，M-Hopfield模型次之。相反，UNB3模型不依赖于实测气象数据，考虑气象元素季节性变化，参考Niell思想，构造海平面上某测站处气象因子同年积日、纬度呈余弦关系的函数，基于美国标准大气资料构建查找表，可根据测站年积日、纬度直接获取该测站气象参数，将其输入模型计算测站天顶延迟。可知，该模型获取气象参数值与测站气象因子变化稳定与否无关。因此，UNB3模型较适用于香港地区气象因子变化相对较大，尤其是湿度变化明显的低压高温高湿气候条件下相对动态定位。由于气象因子变化较快，获取实时准确可靠的测站气象数据用于模型改正较为困难且解算难度增加，关键是难以保证基于实时气象数据进行坐标解算结果的准确性。相比之下，采用UNB3这类经验模型改正延迟在气象参数变化较快大时，能获取更高效、稳定的结果。但因UNB3模型依据历史气象数据规律来计算测站气象参数，没有考虑实际气象条件变化，在气候条件发生较大变化时，可能会使定位结果过于平滑而产生与实际结果不完全贴合的情况。所以，通过实验分析各模型在不同地区、不同气候条件下的性能，可为精密定位合理选取对流层改正模型提供参考。

4 结束语

本文采用相对动态定位手段，基于团队研发的GCC-RTK软件平台，针对不同气候条件下对流层模型适用性能进行定位实验并对结果、模型精度加以分析，得到以下结论：

1）不同气候条件下，3种对流层延迟改正模型解算测站坐标偏差序列分布规律变化趋势大体相似，在低压高温高湿条件下坐标偏差序列波动更为剧烈且产生较大峰值，尤其在垂直方向上更加明显，各模型坐标解算精度相对更低且模型间精度差异较大。2）当日气象因子的变化可在一定程度上反映出各对流层模型ZTD值序列波动，ZTD值受温度、相对湿度的影响要高于气压。3）同一地区不同气候条件下，各对流层模型适用性不同，在香港地区，高压低温低湿环境下，Saastamoinen模型表现更优，尤其是在U方向上精度表现更为显著，M-Hopfield模型次之；而在低压高温高湿环境下，UNB3模型整体表现效果更好。4）不同气候条件下，应用3种模型进行对流层延迟改正定位结果表明：高压低温低湿环境下，模糊度固定率比低压高温高湿环境高约15 %；UNB3模型定位模糊度固定率高于Saastamoinen和M-Hopfield模型定位模糊度固定率，且后2种模型定位模糊度固定率相差不大。

[1] 姚宜斌, 赵庆志. GNSS 对流层水汽监测研究进展与展望[J]. 测绘学报, 2022, 51(6): 935-952.

[2] 施展, 孟祥广, 郭际明, 等. GPS 精密单点定位中对流层延迟模型改正法与参数估计法的比较[J]. 测绘通报, 2009(6): 9-11.

[3] 毛健, 崔铁军, 李晓丽, 等. 融合大气数值模式的高精度对流层天顶延迟计算方法[J]. 测绘学报, 2019, 48(7): 862-870.

[4] 姚宜斌, 胡羽丰, 张豹. 利用多源数据构建全球天顶对流层延迟模型[J]. 科学通报, 2016, 61(24): 2730-2741.

[5] 韩伟. 中国地区对流层延迟模型研究[D]. 东南大学, 2016: 2-2.

[6] TUKA A, EL-MOWAFY A. Performance evaluation of different troposphere delay models and mapping functions[J]. Measurement, 2013, 46(2): 928-937.

[7] SAASTAMOINEN J. Contributions to the theory of atmospheric refraction[J]. Bulletin Géodésique (1946-1975), 1972, 105(1): 279-298.

[8] SAASTAMOINEN J. Contributions to the theory of atmospheric refraction[J]. Bulletin Géodésique (1946-1975), 1973, 107(1): 13-34.

[9] HOPFIELD H S. Tropospheric effect on electromagnetically measured range: Prediction from surface weather data[J]. Radio Science, 1971, 6(3): 357-367.

[10] BLACK H D. An easily implemented algorithm for the tropospheric range correction[J]. Journal of Geophysical Research: Solid Earth, 1978, 83(B4): 1825-1828.

[11] ZHANG H, YUAN Y, LI W, et al. Assessment of three tropospheric delay models (IGGtrop, EGNOS and UNB3m) based on precise point positioning in the Chinese region[J]. Sensors, 2016, 16(1): 122.

[12] LIU L L, ZHOU M, ZHANG T X, et al. Assessment of EGNOS Model over Asia area using IGS_ZTD[C]// Applied Mechanics and Materials. [S.l.]: Trans Tech Publications Ltd., 2014, 501: 2182-2186.

[13] LEANDRO R F, LANGLEY R B, SANTOS M C. UNB3m_pack: A neutral atmosphere delay package for radiometric space techniques[J]. GPS Solutions, 2008, 12(1): 65-70.

[14] BÖHM J, HEINKELMANN R, SCHUH H. Short note: A global model of pressure and temperature for geodetic applications[J]. Journal of Geodesy, 2007, 81(10): 679-683.

[15] LAGLER K, SCHINDELEGGER M, BÖHM J, et al. GPT2: Empirical slant delay model for radio space geodetic techniques[J]. Geophysical Research Letters, 2013, 40(6): 1069-1073.

[16] NIELL A E. Global mapping functions for the atmosphere delay at radio wavelengths[J]. Journal of Geophysical Research: Solid Earth, 1996, 101(B2): 3227-3246.

[17] BÖHM J, NIELL A, TREGONING P, et al. Global mapping function (GMF): A new empirical mapping function based on numerical weather model data[J]. Geophysical Research Letters, 2006, 33(7).

[18] KOUBA J. Implementation and testing of the gridded Vienna mapping function 1 (VMF1)[J]. Journal of Geodesy, 2008, 82(4): 193-205.

[19] 张双成, 叶世榕, 刘经南, 等. 动态映射函数最新进展及其在GNSS遥感水汽中的应用研究[J]. 武汉大学学报(信息科学版), 2009, 34(3): 280-283.

[20] 章浙涛. GNSS非模型化误差处理理论与方法[J]. 测绘学报, 2020, 49(7): 936.

[21] 李媛, 章浙涛, 何秀凤, 等. 雨雪天气对流层延迟改正模型适用性分析[J]. 导航定位学报, 2022, 10(2): 119-125.

[22] 黄东桂, 刘立龙, 黄良珂, 等. 桂林地区暴雨天气下两种对流层模型的适用性分析[J/OL]. 桂林理工大学学报: 1-8[2022-10-07] .

[23] 许艳, 杨元喜, 许国昌. 极地GPS定位中的对流层延迟分析[J]. 大地测量与地球动力学, 2014, 34(1): 104-107.

[24] 徐优伟, 张胜凯, 鄂栋臣, 等. 4种对流层模型在南极地区的适用性分析[J]. 测绘地理信息, 2016, 41(4): 18-22.

[25] 杨玲, 李博峰, 楼立志. 不同对流层模型对GPS定位结果的影响[J]. 测绘通报, 2009(4): 9-11, 64.

[26] 王利杰, 李思敏, 蔡成林, 等. 基于不同高度角的对流层延迟改正模型选择[J]. 测绘通报, 2013(8): 10-13.

[27] 邹进贵, 马佑, 肖扬宣, 等. 对流层延迟模型对GPS高程时间序列的影响分析[J]. 测绘地理信息, 2016, 41(5): 8-11.

[28] 周淼, 刘立龙, 张腾旭, 等. 顾及高程影响的区域天顶对流层延迟改正模型[J]. 桂林理工大学学报, 2014, 34(4): 723-727.

[29] ZHANG J H. Investigations into the estimation of residual tropospheric delays in a GPS network[M]. University of Calgary, 1999.

[30] 章迪. GNSS对流层天顶延迟模型及映射函数研究[D]. 武汉大学, 2017: 16-17.

Performance analysis of several tropospheric models under different climatic conditions

DAI Qi1,ZHANG Zhetao1, WEN Yuanlan1, ZENG Ping1, WANG Miaomiao2

（1. School of Earth Sciences and Engineering, Hohai University, Nanjing, Jiangsu 211100, China;2. School of Computer Information Engineering, Changzhou Institute of Technology, Changzhou, Jiangsu 213032, China）

Tropospheric delay is one of the most important error sources of high precision positioning measurement in Global Navigation Satellite System (GNSS). Aiming at the insufficient analysis of the tropospheric model performance under different climatic conditions, this paper carried out relative kinematic positioning experiments to determine the applicability of different tropospheric models and evaluate the accuracy of three tropospheric models including Saastamoinen, Modified Hopfield (M-Hopfield) and UniversityofNewBrunswick3(UNB3).The experimental results showed that: Under the conditions of low pressure, high temperature and high humidity, the fluctuation of coordinate deviation sequence was relatively violent and had multiple peaks in the vertical direction. Besides, the coordinate solution accuracy of each model was relatively lower and the accuracy difference between models was larger, and the overall correction effect of UNB3 model was better. Under the conditions of high pressure, low temperature and low humidity, Saastamoinen model was more suitable, especially in the vertical direction, followed by M-Hopfield model. Meteorological factors (air pressure, air temperature and relative humidity) affected the tropospheric delay, and the degree of influence of air pressure was relatively lower than that of air temperature and relative humidity. The fixed rate of ambiguity under the conditions of high pressure, low temperature and low humidity was about 15% higher. In addition, the fixed rate of ambiguity of UNB3 model positioning was higher than that of Saastamoinen and M-Hopfield models, and the fixed rate of ambiguity of the latter two models had little difference.

global navigation satellite system (GNSS); relative kinematic positioning; tropospheric correction model; climatic conditions

戴祺, 章浙涛, 文援兰, 等. 不同气候条件下几种对流层模型性能分析[J]. 导航定位学报, 2023, 11(4): 38-48.（DAI Qi, ZHANG Zhetao, WEN Yuanlan, et al. Performance analysis of several tropospheric models under different climatic conditions[J]. Journal of Navigation and Positioning, 2023, 11(4): 38-48.）DOI:10.16547/j.cnki.10-1096.20230406.

P228

A

2095-4999(2023)04-0038-11

2022-12-06

国家自然科学基金项目（41974001，42004014）；江苏省自然科学基金青年基金项目（BK20200530）。

戴祺（1998—），男，福建三明人，硕士，研究方向为GNSS对流层。

文援兰（1965—），男，湖南醴陵人，博士，教授，研究方向为卫星导航与定位、大地测量数据处理理论与方法。