GNSS接收机晶振频率稳定度仿真分析

代培培，王腾飞，姚 铮，邢建平

GNSS接收机晶振频率稳定度仿真分析

代培培1，王腾飞2,3，姚 铮2,3，邢建平1

（1. 山东大学 微电子学院，济南 250100；2. 清华大学 北京信息科学与技术国家研究中心，北京 100084；3. 清华大学 电子工程系，北京 100084）

针对全球卫星导航系统（GNSS）提供的高精度定位、导航及授时（PNT）服务以精密测量的传输时间为基础，然而GNSS接收机中普遍采用的频率源为稳定度较差的晶振的问题，提出一种对GNSS接收机晶振频率稳定度进行分析和建模的方法：根据GNSS接收机晶振频率稳定度受随机频率误差及老化率的影响的原理，给出晶振随机频率误差及老化率的数学模型；并根据不同随机频率误差成分仿真相应的各项晶振随机频率误差序列；同时基于LAG1自相关法辨识不同时期主导的随机频率误差类型，定性分析其对晶振频率稳定度的影响。实验结果表明，提出的方法可为GNSS接收机晶振设计及频率稳定度能评估提供参考。

全球卫星导航系统（GNSS）接收机；晶振；随机频率误差；老化率；阿伦（Allan）方差；LAG1自相关

0 引言

在高精度导航定位授时中，精确的时间是十分重要的。如今在全球卫星导航系统中，为了能够给用户提供高精度的定位、导航及授时（positioning，navigation and timing，PNT）服务，卫星端均搭载了稳定度更高的高精度原子钟，比如铷钟、铯钟或氢钟[1]。然而，用户端的导航定位授时性能依赖于全球卫星导航系统（global navigation satellite system，GNSS）接收机对卫星信号的高精度观测[2-3]，因此，接收机的时钟稳定度有着至关重要的作用。GNSS接收机时钟在满足精度要求的同时，还须兼顾体积、功耗和成本。由于高精度原子钟的价格较高，并且对运行环境要求极高，因此具备低功耗、低价格及体积更小等优势的晶振获得了广泛的关注[4]。目前大多数GNSS接收机的时钟为晶振，常用于校准和频率传递；然而晶振频率稳定度变化会导致接收机对卫星信号的测量产生误差[5]，从而叠加在伪距和载波相位的测量值上。其中，随机频率误差[6-7]及老化率[8-9]是引起晶振频率稳定度变化的重要因素。随机频率误差主要影响晶振的短期频率稳定度，老化率主要影响晶振的长期频率稳定度。因其误差特性十分复杂，很难进行实时精确建模来消除对GNSS接收机服务精度的影响。因此，研究基于GNSS接收机晶振的误差特性及评估分析其对晶振频率稳定度的影响具有十分重要的意义。

本文通过不同随机频率误差成分仿真相应的各项晶振随机频率误差序列，同时基于LAG1自相关法辨识不同时期主导的随机频率误差类型，从而定性分析其对晶振频率稳定度的影响，为GNSS接收机性能评估提供参考。首先阐述晶振频率稳定度的分析方法及随机频率误差特性；然后针对晶振的随机频率误差，即5种独立的幂率噪声建立数学模型，并采用LAG1自相关法对幂率噪声进行识别，仿真分析其对晶振频率稳定度的影响；最后针对晶振的老化率，采用可更准确拟合晶振老化率的经典老化率对数模型，定性分析老化率对晶振频率稳定度的影响。

1 晶振频率稳定度分析方法

1.1 晶振信号的数学模型

晶振的输出信号一般为正弦波，可表示为[10-11]

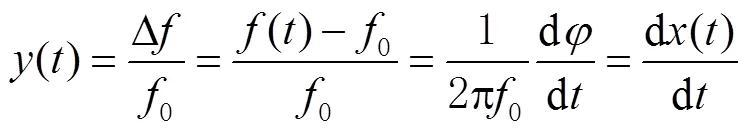
为方便分析晶振频率稳定度，建立晶振模型的输出频率数据随机数，采用随机生成的方法仿真晶振输出的频率数据，此数据未添加任何影响[12]。如图1所示的仿真晶振输出频率数据的时间-频率图可以看出晶振频率在标称频率附近波动，因此能够仿真包含噪声的晶振输出频率。

图1 仿真晶振输出频率数据的时间-频率

1.2 稳定度分析方法

2 晶振随机频率误差数学模型及分析方法

2.1 晶振随机频率误差数学模型

晶振的随机频率误差为幂率噪声，主要由白调相噪声、白调频噪声、闪烁调相噪声、闪烁调频噪声以及随机游走调频噪声5种独立的噪声组成。美国学者大卫·莱森（David Lesson）给出了经典的幂率噪声模型[14]，可表示为

因此，晶振噪声频谱分量与Allan方差之间的转换可表示为[13]

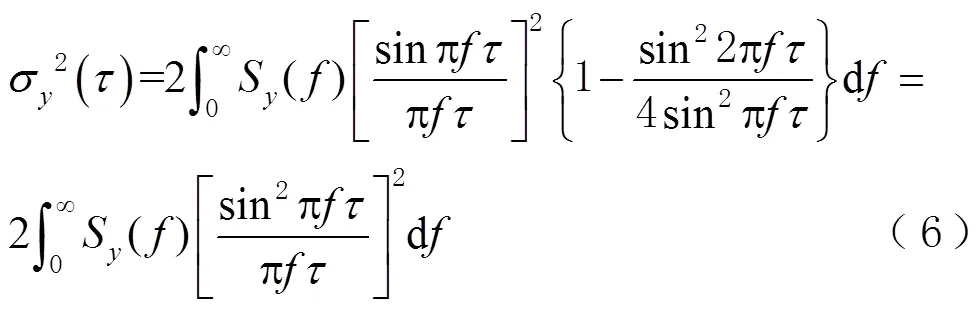
结合式（5）和式（6），可以得到噪声频谱密度的Allan方差的时域，表示为

根据前面所提到的5种噪声之间是相互独立的随机过程，晶振噪声的Allan方差可表示为[15]

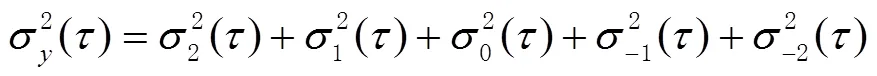
2.2 晶振随机频率误差仿真方法

本文根据典型时间间隔的Allan方差值，仿真晶振5种幂率噪声频率序列。其中，白调相噪声、白调频噪声、随机游走噪声可采用蒙特卡洛仿真方法，闪烁噪声为1/噪声[16]，其功率谱为幂函数，可通过利用频域波形，将白噪声整形成为1/噪声，逆变换生成时域1/噪声序列。

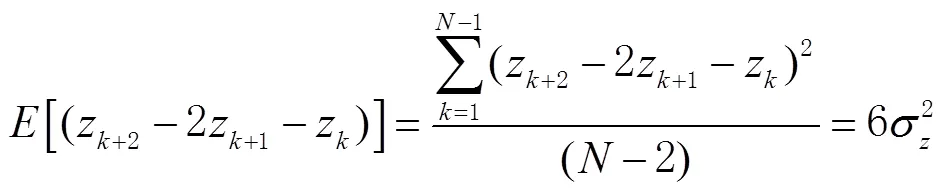
由式（10）可得频率数据序列为

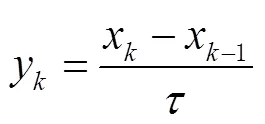
由式（10）可得相位数据序列为

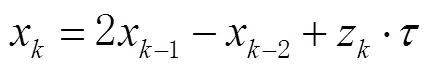
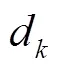
2.3 晶振噪声类型识别方法

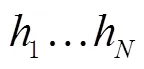
3 实验与结果分析

3.1 晶振随机频率误差仿真分析

本文仿真的对象为10 MHz TCXO晶振，根据文献[15]提供的该晶振不同时间间隔的经典Allan方差平方根值进行仿真分析，如表1所示。

表1 典型Allan方差平方根值

图3 各项噪声的频率稳定度比较

在实际应用中，更关注的是不同时期噪声的识别；因此，本文采用LAG1自相关法通过估计其幂率指数对上述仿真噪声进行分类识别。图4给出了LAG1自相关法识别各项噪声自相关函数图以及相位数据的滞后散点图，同时给出了估计的幂律指数值，可通过幂律噪声系数的识别区间得到相应时期的主导噪声类型。其中，相位数据的滞后散点图为表示数据相关程度的另一种方式，散点的线性拟合斜率和LAG1密切相关。滞后散点图是白噪声的一组不相关点，对于相关性更强的闪烁噪声和随机游动噪声表现出线性特征。当滞后间隔等于或接近周期的1/4时，具有正弦分量的噪声呈现出圆形分布特征。

3.2 老化率对晶振频率稳定度的影响分析

在中短期影响晶振频率稳定度的主要因素是幂率噪声；对于晶振长期频率稳定度的影响占主导地位的是晶振的老化率，其会造成晶振输出频率产生缓慢漂移。Filter.R.L[9]通过大量的实验研究，发现晶振的老化率随时间的增加而减小；因此，线性模型不能准确表征晶振的老化率。同时，晶振的老化率以对数曲线形式呈现，给出了对数函数模型，能够更准确地拟合晶振老化率的实际情况。Viq.J.R[8]给出了经典老化率数学模型，如图5所示。

图5 经典的晶振老化率数学模型

采用随机生成的方法仿真受老化率影响的晶振输出频率数据。由如图6（a）所示的老化率影响的晶振输出时间-频率图可以看出，晶振频率前期在标称频率附近波动，随着时间的增加，老化率影响逐渐显现，呈现出不太标准的正态分布。由如图6（b）所示的老化率影响的晶振输出频率直方图可知，该方法能够仿真受老化率影响的晶振输出频率数据。

基于上述晶振输出频率数据，分析其频率稳定度，如图7所示给出了老化率影响下晶振频率稳定度结果。从图中可以看出，前期晶振老化率随着时间的增加而减小，在后期又逐渐增大并趋于平稳，符合实际晶振老化率的情况。

图6 仿真老化率影响的晶振输出频率数据的时间-频率及频率直方图

图7 老化率影响下晶振频率稳定度结果

4 结束语

本文针对随机频率误差及老化率对GNSS接收机晶振频率稳定度的影响进行仿真分析。首先推导了晶振的随机频率误差数学模型，通过对晶振随机频率误差的仿真分析，得出晶振频率偏移程度随着采样间隔的增大而减小，并且随着采样时间的增加，在不同时期主导噪声影响不同的结论：在中期，随机游走调频噪声和闪烁调频噪声为主导噪声；在短期，随机游走噪声和白调相噪声为主导噪声。其次，本文采用LAG1自相关法通过估计其幂率指数对上述仿真噪声进行分类识别，验证了晶振随机频率误差数学模型的正确性。最后，采用经典老化率对数数学模型，通过仿真分析老化率对晶振频率稳定度的影响，得出晶振的老化率随时间的增加而减小最后趋于平缓，符合实际情况的结果。因此，通过仿真分离老化率及随机频率误差对晶振频率稳定度的影响，可以为GNSS接收机晶振设计及频率稳定度评估提供参考。

[1] 郭海荣. 导航卫星原子钟时频特性分析理论与方法研究[D]. 郑州: 信息工程大学, 2006.

[2] 黄观文. GNSS星载原子钟质量评价及精密钟差算法研究[D]. 西安: 长安大学, 2012.

[3] 王嘉琛, 樊多盛, 肖波, 等. 基于晶振的远程时间同步参考源性能分析[J]. 时间频率学报, 2020, 43(4): 270-278.

[4] 彭慧丽, 陈金和, 韩艳菊, 等. 高频高稳恒温晶体振荡器设计[J]. 宇航计测技术, 2020, 40(1): 46-50．

[5] Allan D W, Levine J. A historical perspective on the development of the Allan variances and their strengths and weaknesses[J]. IEEE Transactions on Ultrasonics Ferroelectrics＆ Frequency Control, 2016, 63 (4) : 513-519.

[6] Rutman J. Characterization of phase and frequency instabilities in precision frequency sources: Fifteen years of progress[J]. Proceedings of the IEEE, 1978, 66(9): 1048-1075.

[7] Vig J R. Quartz crystal resonators and oscillators for frequency control and timing applications: A tutorial[J]. Nasa Sti/recon Technical Report N, 1994, 95: 19519.

[8] Vig J R. The aging of bulk acoustic wave resonators, filters and oscillators[C]// Proceedings of the 45th Annual Symposium on Frequency Control 1991. [S.l.]: IEEE, 1991: 77-101.

[9] Filter R L, Vig J R. Long-Term aging of oscillators[J]. IEEE Transactions on Ultrasonics, Ferroelectrics and Control, 1993, 40(4): 387-394.

[10] 孙江涛. 基于GPS的1PPS的二级频标驯服技术[D]. 西安:西安电子科技大学, 2010.

[11] 鲁刚. 基于GNSS的晶振驯服与保持技术研究[D]. 北京: 中国科学院大学(中国科学院国家授时中心), 2021.

[12] 贾丽娜, 彭慧丽, 于德江, 等. 高稳晶振短期频率稳定度的仿真分析[J]. 宇航计测技术, 2021, 41(3): 27-33.

[13] Riley W J. Handbook of frequency stability analysis[Z]. National Institute of Standards and Technology: Gaithersburg, MD, USA, 2008.

[14] Guo W. Estimations of frequency and its drift rate[J]. IEEE Transactions on Instrumentation and Measurement, 1997, 46(1): 79-82.

[15] 寇艳红, 张其善. GPS接收机中晶振误差的模拟方法[J]. 电子与信息学报, 2004, 26(8): 1319-1324.

[16] 冯爱明, 林敏. 利用几何插值法合成1/f噪声[J]. 中国计量学院学报, 2002, 13(2): 109-112.

[17] 孙宏伟. 原子钟噪声的蒙特卡络模拟方法[J]. 时间频率学报, 1996, 19(0): 33-37.

[18] Riley W J. User manual: Stable32 frequency stability analysis[Z]. Hamilton Technical Services, Beaufort, South Carolina, 2007.

Simulation analysis on frequency stability of crystal oscillator in GNSS receivers

DAI Peipei1, WANG Tengfei2,3, YAO Zheng2,3, XING Jianping1

（1. School of Microelectronics, Shandong University, Jinan 250100, China;2. Beijing National Research Center for Information Science and Technology, Tsinghua University, Beijing 100084, China;3. Department of Electronic Engineering, Tsinghua University, Beijing 100084, China）

Aiming at the problem that the high-precise positioning, navigation and timing (PNT) services provided by the global navigation satellite system (GNSS) are based on precisely measured transmission time, but the frequency source commonly used in the GNSS receivers is crystal oscillators with poor stability, the paper proposed an analysis and modelling method of the frequency stability of crystal oscillatorin GNSS receivers: according to the principle that the crystal frequency stability of GNSS receivers is affected by random frequency error and aging rate, the mathematical model of the random frequency error and the aging rate was given; and the corresponding random frequency error sequences of crystal oscillator were simulated according to different random frequency error components; meanwhile, the dominant random frequency error types in different periods were identified based on the LAG1 autocorrelation method, to qualitatively analyze their influence on the frequency stability of crystal oscillator. Experimental result showed that the proposed method could provide a reference for the design of crystal oscillator in GNSS receivers and the performance evaluation of the frequency stability.

global navigation satellite system (GNSS) receiver; crystal oscillator; random frequency error; aging rate; Allan variance; LAG1 autocorrelation

代培培, 王腾飞, 姚铮, 等. GNSS接收机晶振频率稳定度仿真分析[J]. 导航定位学报, 2023, 11(4): 90-96.（DAI Peipei, WANG Tengfei, YAO Zheng, et al. Simulation analysis on frequency stability of crystal oscillator in GNSS receivers[J]. Journal of Navigation and Positioning, 2023, 11(4): 90-96.）DOI:10.16547/j.cnki.10-1096.20230413.

P228

A

2095-4999(2023)04-0090-07

2022-10-24

国家重点研发计划项目（2021YFA0716603）；国家自然科学基金面上项目（42274018）；第六届中国科协青年人才托举工程支持项目（YESS20200226）。

代培培（1993—），女，山东聊城人，博士研究生，研究方向为GNSS定位授时算法。