定时截尾样本下广义逆指数分布参数的Bayes估计
2023-08-23刘华习长新
刘华,习长新
(荆楚理工学院数理学院,湖北 荆门 448000)
0 引言
广义逆指数分布是Abouammoh和Alshingiti于2009年将广义指数分布和逆指数分布结合后提出的一种新的分布[1],它是逆指数分布的推广,在工程和技术科学中有广泛的应用;且Krishna和Kumar(2013)[2]已经通过实例证明在多数情况下广义逆指数分布比指数分布、逆指数分布、Weibull分布、伽玛分布有更好的适用性。近几年国内外很多学者开始研究这个分布的统计性质,文献[3]在逐步Ⅱ型截尾样本下证明了广义逆指数分布形状参数的最大似然估计的存在性和唯一性;文献[4]基于首次失效逐次截尾样本研究了广义逆指数分布参数的点估计和区间估计;文献[5]在恒定应力加速寿命试验中首先研究了广义逆指数分布参数的极大似然估计,然后利用最小二乘法、加权最小二乘法、百分位估计法等九种方法研究了参数的估计,最后通过数值模拟进行比较;文献[6]在一般逐步Ⅱ型删失样本下研究了广义逆指数分布参数的极大似然估计和Bayes估计;文献[7]研究了URV和URRSS下广义逆指数分布在平方损失和Linex损失下参数的Bayes估计;文献[8]在Ⅱ型截尾样本下研究了广义逆指数分布形状参数的最大似然估计和E-Bayes估计;文献[9]在Ⅱ型混合截尾样本下研究了广义逆指数分布参数的最大似然估计并构造了参数的渐近置信区间,运用Lindley,s逼近方法和Tierney Kadane逼近方法得出了参数的Bayes估计。以上文献获取试验数据采用了定数截尾方法,定时截尾试验也是一种常见的获取数据的方式,目前只有文献[10]研究了广义逆指数分布在定时截尾下的参数估计问题,其主要研究在双边定时截尾样本下广义逆指数分布形状参数的最大似然估计和EM估计,通过数值模拟得到EM估计效果相对较好。在定时截尾样本下,有许多学者[11—17]研究了其他分布的参数估计问题,但是在定时截尾样本下广义逆指数分布参数的Bayes估计暂时没有学者研究。本文拟在定时截尾样本下给出广义逆指数分布的形状参数、可靠度、危险率的极大似然估计和Bayes估计,并通过数值模拟比较估计效果。
广义逆指数分布的分布函数和概率密度函数分别为:
若用t表示产品的寿命,则可靠度函数和危险率函数分别为:
其中,式(1)和式(2)的参数α(>0)和β(>0)分别称为形状参数和尺度参数,当α=1时,为逆指数分布。
本文假设产品寿命服从广义逆指数分布,假定分布中尺度参数β已知,基于定时截尾样本对形状参数、可靠度和危险率进行统计分析。
1 形状参数的极大似然估计
假设现有一批寿命服从广义逆指数分布的产品,从中随机抽取n个产品进行试验,对应失效时刻分别为X1,X2,…,Xn,在时刻0开始进行跟踪观察,进行到预先设定的时间T(T>0)时结束试验,其余没有失效的产品全部撤离试验,并假定到时刻T时至少有一个产品失效,此为定时截尾试验。广义逆指数分布在定时截尾试验下得到的样本观察值记为:
定时截尾样本的联合似然函数为:
其中,C(>0)为常数,与α无关。对式(3)取对数后求α的偏导数,并令=0,得:
计算得α的极大似然估计为:
根据极大似然估计的不变性,可靠度R(t)和危险率H(t)的极大似然估计分别为:
2 形状参数的Bayes估计
2.1 熵损失函数下形状参数的Bayes估计
定义1[18]:设随机变量X服从概率密度函数为f(x,α)的分布,其中α为参数,如果δ是α判别空间中的一个估计,则熵损失函数为似然比对数函数的数学期望:
根据定义1,广义逆指数分布的熵损失函数为:
经化简得:
令M=1-,对式(6)计算关于α的后验期望,得:
欲使式(7)达到最小,只需要对式(7)计算关于δ(Y)的一阶偏导数,并令偏导数为0,得:
本文选取α的共轭先验分布为指数分布,其概率密度函数为π(α)=λe-λα(其中λ>0为超参数)。由Bayes公式可得α的后验概率密度函数为:
故:
定理1:在定时截尾样本下,损失函数为熵损失函数,当取α的先验分布为指数分布时,广义逆指数分布参数α的Bayes估计为:
且该估计是唯一的。
证明:
再由式(9)得到熵损失函数下α的Bayes估计为:
由熵损失函数下参数α的Bayes估计的推导过程可知,此估计具有唯一性。
2.2 平方损失函数下形状参数的Bayes估计
定理2:在定时截尾样本下,当损失函数为平方损失时,取α的先验分布为指数分布,则广义逆指数分布参数α的Bayes估计为。
证明:因为在平方损失函数下,α的Bayes估计为其后验分布的均值,即=E(α|Y),而,所以有:
2.3 Linex损失函数下形状参数的Bayes估计
定理3:在定时截尾样本下,若损失函数为Linex损失L(α,δ)=ec(δ-α)-c(δ-α)-1,其中c≠0,取α的先验分布为指数分布,则广义逆指数分布参数α的Bayes估计为:
证明:由文献[19]知在Linex损失下参数α的Bayes估计为,且此估计是唯一的。而E(e-cα|Y),从而在Linex损失下参数α的Bayes估计为:
在Linex损失函数定义中,可以看出,当c>0时,低估造成的损失小于高估;当c<0时,结论相反。因此在后文的数值模拟中主要讨论c>0的情况。
从式(11)至式(13)可以看出,参数α的Bayes估计中都含有超参数λ,故λ也需要进行估计,下面用极大似然估计法研究超参数λ的估计。
2.4 超参数λ的估计
广义逆指数分布的概率密度函数为式(1),α的先验分布为π(α)=λe-λα,则其经验概率密度函数和分布函数分别为:
以f(yi)、F(T)分别代替式(3)中的f(yi,α)、F(T,α),则似然函数式(3)变为:
对上式取对数后求λ的偏导数,并令=0,得:
上式变形为:
式(14)关于λ无显式解,但可以证明此方程的解存在且唯一。
所以g2(λ)在(0,+∞)上是严格单调递减的凹函数。
记式(15)符合预定义精度要求的迭代值为λˆ,将λˆ代入式(11)至式(13)就可求出α的Bayes估计。
2.5 Bayes估计的容许性
引理2[20]:对于给定的Bayes决策问题,若对给定的先验分布π(α),α的Bayes估计δ(X)是唯一的,则δ(X)是容许的。
定理4:对于广义逆指数分布,在定时截尾样本下,取α的先验分布为指数分布,在熵损失、平方损失、Linex损失函数下,α的Bayes估计都是容许的。
证明:由前面证明的定理可知,在熵损失、平方损失、Linex损失函数下,参数α的Bayes估计都是唯一的。再根据引理2可知,α的Bayes估计都是容许的。
3 可靠度和危险率的Bayes估计
定理5:在定时截尾样本下,当β已知时,若α的先验分布为π(α)=λe-λα,则有下列结论:
(1)在熵损失函数下,可靠度函数R(t)的Bayes估计为:
(2)在平方损失函数下,可靠度函数R(t)的Bayes估计为:
(3)在Linex损失函数下,可靠度函数R(t)的Bayes估计为:
证明(1):
从而在熵损失函数下,可靠度函数R(y)的Bayes估计为:
令y=t就得到了t时刻的可靠度R(t)在熵损失函数下的Bayes估计为式(16)。
证明(2):在平方损失函数下,可靠度函数R(y)的Bayes估计为:
令y=t就得到了t时刻的可靠度函数R(t)在平方损失函数下的Bayes估计为式(17)。
证明(3):
从而在Linex损失函数下,可靠度函数R(y)的Bayes估计为:
令y=t就得到了t时刻的可靠度函数R(t)在Linex损失函数下的估计为式(18)。
定理6:在定时截尾样本下,当β已知时,若α的先验分布为π(α)=λe-λα,则有下列结论:
(1)在熵损失函数下,危险率H(t)的Bayes估计为:
(2)在平方损失函数下,可靠度函数H(t)的Bayes估计为:
(3)在Linex损失函数下,可靠度函数H(t)的Bayes估计为:
证明(1):
从而在熵损失函数下,危险率函数H(y)的Bayes估计为:
令y=t就得到了t时刻的危险率函数H(t)在熵损失函数下的Bayes估计为式(19)。
证明(2):在平方损失下,危险率函数H(y)的Bayes估计为:
令y=t就得到了t时刻的危险率函数H(t)在平方损失函数下的Bayes估计为式(20)。
证明(3):
从而在Linex损失函数下,危险率函数H(y)的Bayes估计为:
令y=t就得到了t时刻的危险率函数H(t)在Linex损失函数下的Bayes估计为式(21)。
4 数值模拟
本文利用Matlab软件进行数值模拟,以讨论形状参数的极大似然估计和Bayes估计的效果。对样本容量n、截尾时刻T取不同的值,利用估计均值(MEAN)和均方误差(MSE)来评价参数的估计效果。具体的模拟步骤如下:
步骤1:给定n、T及参数α=3、β=2。
步骤2:生成n个均匀分布随机数ui~U(0,1),由(i=1,2,…,n)生成服从广义逆指数分布的样本x1,x2,…,xn;令2,…,n),生成定时截尾样本序列和。
步骤3:给定λ的初始估计λ0,按照式(15)进行迭代计算超参数λ的估计值,精度取c=10-5。
步骤4:分别按照式(4)、式(11)至式(13)计算α的极大似然估计̂M、熵损失函数下的Bayes估计̂BE、平方损失函数下的Bayes估计̂BS、Linex损失函数下的Bayes估计α̂BL。其中,在Linex损失函数定义中,当c>0时,低估造成的损失小于高估,因此模拟过程中令c=0.8。
步骤5:重复执行步骤2至步骤4共1000次,将得到的α的各种估计值的平均值作为α的最终估计值,并计算均方误差,其中均方误差计算公式为。
步骤6:在不同的n和T下,重复上述过程。
模拟结果见表1。模拟结果表明,在相同条件下,平方损失函数下形状参数α的估计要劣于其他估计。其中,当样本容量小于等于50时,熵损失函数和Linex损失函数下参数α的估计精度较高;当样本容量大于50时,各种估计相差不大,都体现了大样本的性质。随着样本量的增加,α的各种估计均值与真值的偏差及均方误差逐渐减小,说明估计精度在提高。
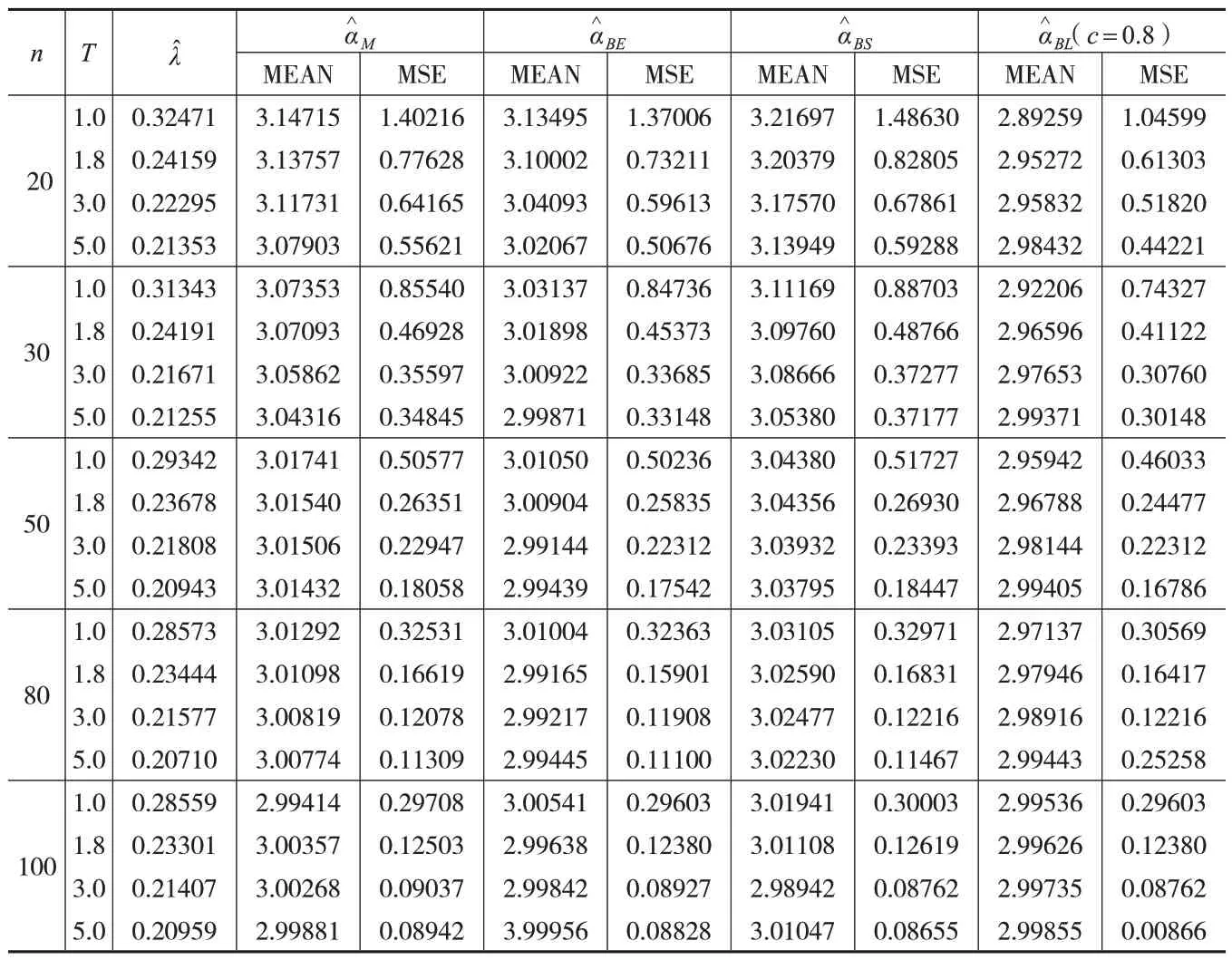
表1 定时截尾样本下广义逆指数分布形状参数α的估计试验结果
产品的可靠度和危险率估计是可靠性理论研究的重要问题之一。类似以上模拟过程,根据式(5)和式(16)至式(21)给出广义逆指数分布产品的可靠度和危险率的各种估计,表2和下页表3分别给出了在不同时刻t可靠度和危险率的极大似然估计和不同损失函数下Bayes估计的均值和均方误差。从可靠度估计的数值模拟结果中可以看出,在相同条件下,可靠度的Bayes估计整体优于最大似然估计,在Bayes估计中Linex损失函数下可靠度的估计的效果最好,特别是在小样本场合Bayes估计的优势更加明显。随着定时截尾时刻T的增加,所有估计的均方误差均在减小。随着样本容量的增加,所有估计的均方误差均逐渐减小,说明估计精度提高了。从危险率估计的数值模拟结果中可以看出,在相同条件下,Linex损失函数下危险率的估计效果较好;随着定时截尾时刻T的增加,所有估计的精度均在提高;随着样本容量的增加,所有估计的精度也均在提高。
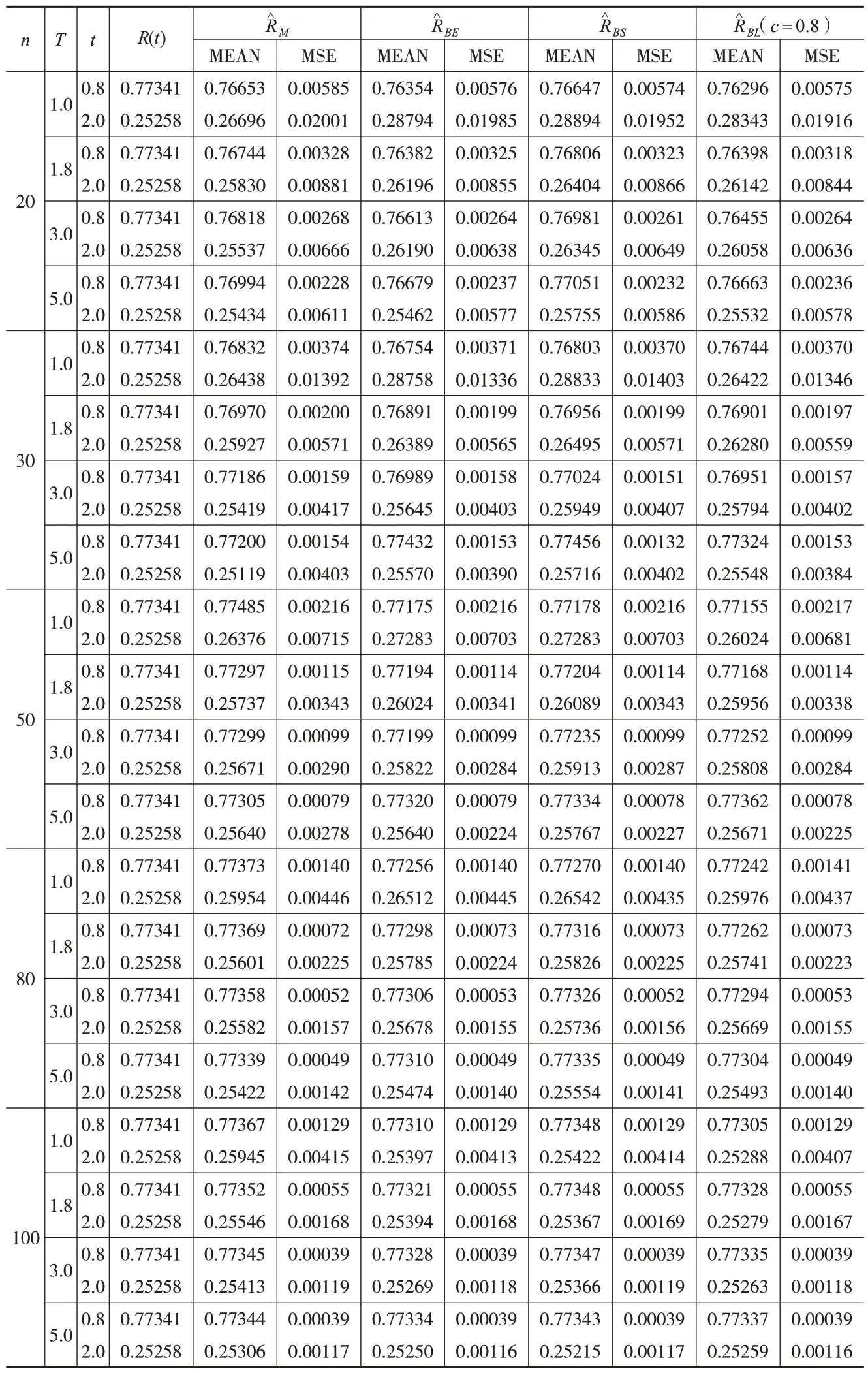
表2 定时截尾样本下广义逆指数分布可靠度R(t)的估计试验结果
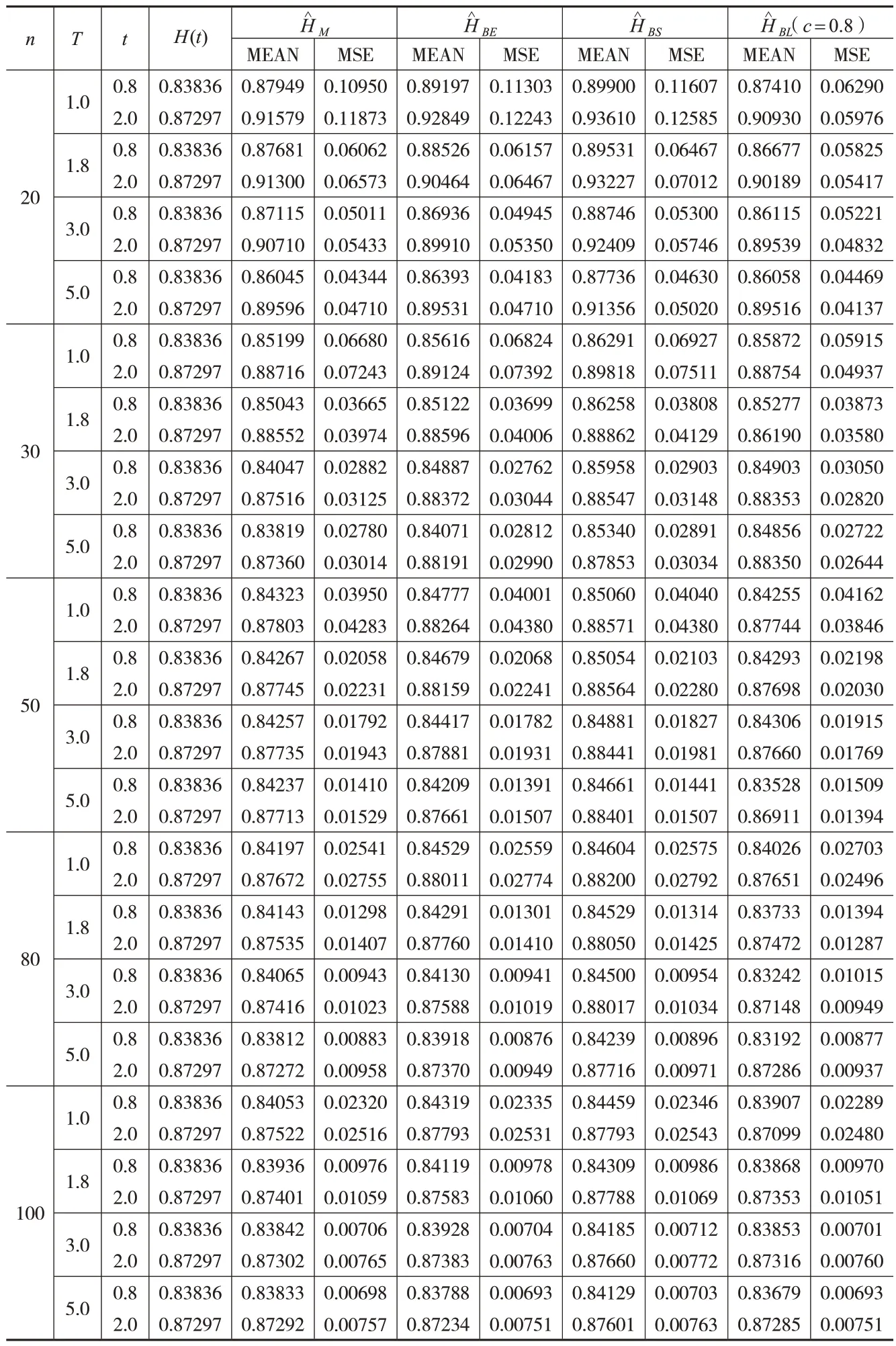
表3 定时截尾样本下广义逆指数分布危险率H(t)的估计试验结果
5 结论
本文在定时截尾样本下,得到了广义逆指数分布的形状参数、可靠度和危险率的最大似然估计和Bayes估计。利用蒙特卡洛方法给出数值模拟,比较了最大似然估计和Bayes估计。其中,形状参数在熵损失和Linex损失函数下的估计精度较高;可靠度的Bayes估计整体优于最大似然估计;危险率在Linex损失函数下的估计效果较好。整体来说,所有估计的精度均随着截尾时间T的增大而提高;同时,随着样本容量的增加,所有估计量的精度也均在逐渐提高。
