对课本上抛物线焦点弦的一个性质两次推广

华南师范大学附属中学(510630) 罗碎海

华南师大附中汕尾学校(516600) 谢贤祖

我们学汉字是一个一个死记硬背的,而学数学却不能这样,要像数数一样往下顺,由前知后、由点知面、举一反三;要注意代数形式与几何内容的统一;要注意普遍性与特殊性之间的联系.以下我们从对课本例题的分析与研究,认真体会数学的学习方法、体会数学的发展变化规律.从而更好的学习数学、应用数学.

引例[1](普通高中教材数学选择性必修第一册第136 页例5)“经过抛物线焦点F的直线交抛物线于A,B两点,经过点A和抛物线顶点的直线交抛物线准线于点M,求证: 直线MB平行于抛物线的对称轴.”(解答见课本[1])

原题翻译成数学语言就是: 过抛物线C:y2=2px焦点的一条直线与抛物线交于两点A,B,通过点A和抛物线顶点O的直线交准线l:x=于点M,求证: 直线轴MB//OX轴(如图1).

图1

探究1该命题的逆命题如何?

逆命题有两种形式:

由于原命题本质是充要条件的命题,所以两个逆命题都为真命题,也可以说是原题的另两种等价形式.

等价形式(1)就为2001 年全国高考题:

“抛物线y2=2px(P >0) 的焦点为F,经过点F的直线交抛物线交于A、B两点,点C在抛物线的准线上,且BC//X轴,证明直线AC经过原点O.”

探究2对抛物线所具有的如上性质,别的圆锥曲线如何?

若将原抛物线换为椭圆,自然得到有下列叙述:

认真推算,发现直线AC并不经过椭圆的左顶点.这种推广不对.是不能推广还是推广的方向搞错了呢? 要注意原题中的元素的多重性质,点O是抛物线的顶点,但也是线段FE的中点,所以还有别的形式.

经过推算,可知(4)是正确的,(3)不正确.“点O是线段FE的中点”才是原题的本质,“点O是抛物线顶点”只是表面现象.到此可得双曲线中相应的命题:

图2

探究3既然三种曲线都具有类似的性质,而三种曲线有统一定义和统一的方程(极坐标方程),那么应该有统一的证明方法吧!

三种曲线的统一证明取F为极点,Fx为极轴,建立极坐标系.设∠AFX=θ,A(ρ1,θ),B(ρ2,θ+π)则

(如图3,上式可在直角坐标系中证明:

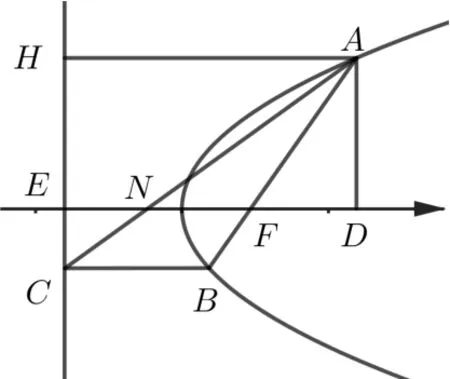
图3

FD=ρ1cosθ,EF+FD=p+ρ1cosθ=AH=所以ρ1=FA=

ρ2=BF=因为NF//CB,所以

根据圆锥曲线第二定义,有e=,所以

又p=|EF|,所以N是EF的中点.

这是一个一般性的结论与一般性的证明.一个特殊例子就是:

探究4 以上问题中涉及的焦点与准线,从更广意义上可认为是极点与极线的特殊问题.那么对一般的极点与极线该问题如何?

进一步探讨有:

(7)更一般的问题: 如图4,过定点P(x0,y0)的直线交椭圆C:=1(a > b >0)于A、B两点,点P不在椭圆C上,过点A作直线=1 的垂线,垂足为E,求证: 直线BE过定点.

图4

分析如图5,不妨设定点P(x0,y0)在椭圆内部,直线l:=1 是点P所对应的极线,延长BA交直线l于点Q,作BH ⊥l于点H,PM ⊥l于点M,设PM与BE交于点T,由极点与极线性质,设=λ[2][3].则

图5

所以

所以PT=MT.所以直线经过定点T,该点是线段PM的中点.

综上,我们得知: 最初问题中的“直线MB平行于抛物线的对称轴”不是问题的本质,本质应是“直线MB垂直于抛物线的准线”.最初的焦点弦性质其实是任意一点与其对应极线的性质.

问题经过抛物线向一般圆锥曲线推广,从焦点与准线向一般极点与极线推广,实现了知识的体系化,实现了认识上的升华.这时,我们的认识已不限于抛物线中,也不限于圆锥曲线的焦点,而是对于任意的圆锥曲线与任意一点可以编制题目,达到了“随心所欲不逾矩”的地步.

任何一个问题的出现,可能是某一问题的特殊情况,我们只有探求其普遍性,才能认识原问题的本质.数学学习是这样,其它问题也是这样,即“透过现象看本质”,而数学教给我们这种思想方法: 注意多重性,追求普遍性.