一道俄罗斯奥数试题的进一步推广

广东省深圳中学(518001) 邱际春

1 问题提出

文[1]中王玉怀老师翻译并介绍了俄罗斯圣彼得堡为纪念瑞士数学家、圣彼得堡科学院院士欧拉(Euler)诞辰300 周年而举办的欧拉数学奥林匹克试题.首先给出其中的一道题目如下:

题目(欧拉数学奥林匹克的第10 题[1])在Rt∆ABC中,∠C=90◦,斜边AB=c,BC=a,CA=b.以斜边c为边,作不包含∆ABC的正方形ABDE.求顶点C与正方形对角线交点的距离.

王玉怀老师对此作初步推广:

推广A[1]在Rt∆ABC中,∠C=90◦,斜边AB=c,BC=a,CA=b.以斜边AB为边,作正方形ABDE.求顶点C与正方形对角线交点的距离.

文[2]针对其中的第10 题进行推广和探究,得到了拓广命题的12 种解法.

考虑在该推广A 命题的基础上初步思考: 如果以斜边AB为边,作菱形ABDE或矩形ABDE,将会产生怎样的结果呢?

2 初步类比

先将文[2]中王玉怀老师的推广命题等价地表述为:

命题1[2]在Rt∆ABC中,∠C=90◦,斜边AB=c,BC=a,CA=b.以斜边AB为边,作正方形ABDE,且对角线交于点M.

(i)若点C,M在直线AB两侧,则CM=

(ii)若点C,M在直线AB同侧,则CM=

笔者在文[3]中采用横向类比推理,将正方形ABDE类比成菱形ABDE或矩形ABDE,得到如下结论:

命题2[3]在Rt∆ABC中,∠C=90◦,AB=c,BC=a,CA=b.以斜边AB为边,作菱形ABDE,且对角线交于点M,约定∠BAD=θ.

(i)若点C,M在直线AB两侧,则CM=acosθ+bsinθ;

(ii)若点C,M在直线AB同侧,则CM=|acosθ−bsinθ|.

命题3[3]在Rt∆ABC中,∠C=90◦,AB=c,BC=a,CA=b.以斜边AB为边,作矩形ABDE,且对角线交于点M,约定∠BAD=θ.

(i)若点C,M在直线AB两侧,则

(ii)若点C,M在直线AB同侧,则

事实上,虽然这三个结论在形式上不太一致,但还算比较优美.若进一步探究,可发现它们依然还有推广的空间.因此,考虑对原题中的直角三角形和正方形分别推广至任意三角形和正n边形,我们能获得什么样的结论呢?

3 统一推广

笔者研究后,给出下面统一的推广命题:

推广已知在∆ABC中,∠C=θ,AB=c,BC=a,CA=b.以斜边AB为边,作正n边形AA1···An−2B,记正n边形的中心为M.

(i)若点C,M在直线AB两侧,则

(ii)若点C,M在直线AB同侧,则

证明设点M为正n边形AA1···An−2B的中心,连接AM,BM和CM.注意到在正n边形AA1···An−2B中,∠AMB=.取AB的中点D,连接CD,DM,则AM=BM,且DM垂直平分AB.于是,

在∆BMD中,由正弦定理可得所以

在等腰∆ABM中,由勾股定理可得

所以BM=

(1)若点C,M在直线AB两侧时(如图1);

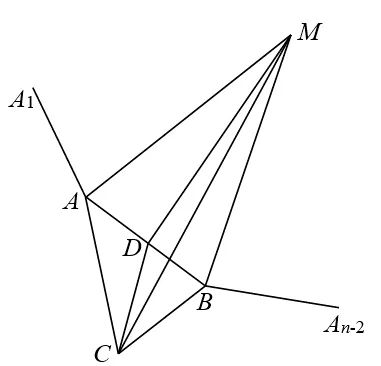
图1

由正弦定理和余弦定理可得

在∆CBM中,由余弦定理可得

(2)若点C,M在直线AB同侧时,存在如下三种情形:

①当点C落在直线BM左侧时,如图2 所示.

图2

由正弦定理和余弦定理可得

在∆CBM中,由余弦定理可得

②当点C落在直线BM上(如图3),则CM=

图3

注意到cos ∠CBM=1,而

③当点C落在直线BM右侧时,如图4 所示.

图4

由于

cos ∠CBM=cos(∠ABC−∠ABM)=cos(∠ABM−∠ABC),下同情形①.

综上所述,若点C,M在直线AB两侧时,则

若点C,M在直线AB同侧时,则

4 进一步反思

至此,我们已经得到了一般性的推广结论,这是因为在推广中取θ=,n=4,有a2+b2=c2,即可得到命题1.如果在上述推广命题中分别依次取n=4 和θ=时,还可推出下面两个优美的推论:

推论1 已知在∆ABC中,∠C=θ,AB=c,BC=a,CA=b.以AB为边,作正方形ABDE,且对角线交于点M.

(i)若点C,M在直线AB两侧,则

(ii)若点C,M在直线AB同侧,则

推论2 在Rt∆ABC中,∠C=,AB=c,BC=a,CA=b.以斜边AB为边,作正n边形AA1···An−2B,记正n边形的中心为M.

(i)若点C,M在直线AB两侧,则CM=

(ii)若点C,M在直线AB同侧,则CM=

事实上,推论1 可以看成是命题1 在角度上的推广,即将Rt∆ABC推广成任意三角形; 推论2 可以看成是命题1 在边数上的推广,即将正方形ABDE推广成正n边形AA1···An−2B.