不同突触的神经元网络同步放电比较研究

刘瑾琬

（兰州交通大学，兰州 730070）

人脑中的神经系统是一个非常复杂的多功能系统，由千亿个神经突触连接的神经元构成，具有复杂的网络动力学行为，是生物信息的进行传递、整合与协调的中枢， 为研究神经系统放电活动和信息行为提供了新的角度。研究神经网络的放电过程，有助于探究神经信息编码机制，是脑科学研究领域的重要内容[1]。

Stevens 等[2-3]研究发现，神经元之间放电序列的相关性和同步放电现象可以有效抑制噪声对编码的影响，提高编码效果，保证神经信息编码的可靠性。 常小龙等[4]采用FHN 神经元作为网络节点搭建了神经元网络，通过数值模拟的方法，研究并讨论了神经网络的同步放电特性，并对其与抗扰能力进行了分析计算。上述研究从神经信息处理角度研究了神经系统同步放电机制，但是研究中选用的多为较低维度的神经元模型，不能精确模拟真实神经元电生理特性。

本文选取最接近生物学实际的Hodgkin-Huxley（ HH）模型，基于MATLAB&Simulink 平台，采用数值模拟的方法分别搭建由电突触和化学突触连接的具有生物特性的复杂神经元网络， 对比分析了神经突触对神经元网络的同步放电特性的影响。

1 研究方法

1.1 Hodgkin-Huxley 模型

HH 模型在1952 年由Hodgkin 和Huxley 提出[5-8]，通过一组四阶非线性微分方程描述了乌贼轴突细胞膜动作电位产生和传导的过程， 能够准确地解释实验结果，如式（ 1）所示

式中：I 为外部刺激电流，C 为细胞膜单位面积的电容，值为1 μV/cm2；V 是膜电压， 初值-65 mV；GNa和GK分别代表钠离子通道、钾离子通道的最大电导，值分别为120 mS/cm2、360 mS/cm2；GL为漏电导，值为0.3 mS/cm2；ENa、EK、EL分别为钠离子通道、钾离子通道、漏电流的反转电势，值分别为50 mV，-77 mV，-54.5 mV；m 和h分别为钠离子通道电导的激活变量和抑制变量，n 为钾离子通道的激活变量，α 和β 是与膜电位有关而与时间无关的速率函数。

1.2 突触模型

大脑神经系统中信号的传递、整合的过程需要依赖神经突触连接构成的神经回路。神经突触作为神经元之间相互联系并通信的部位， 包括电突触和化学突触2类。 化学突触广泛存在于生物体神经系统中，电突触是一种简单的神经元之间的电耦合关系，一般存在于低等动物的神经系统中。 电突触数学模型如式（ 2）所示

式中：Isyn为电突触耦合电流，g 为突触耦合强度，V 为突触前神经元动作电位，V1为突触后神经元动作电位， 此电流为突触前神经元对突触后神经元通过电突触耦合产生的突触电流。

Savtchenko[9]研究并提出了一个复杂的动力学模型， 该模型能够精确描述化学突触进行信息传递的过程且更接近于生物学实际， 故本文选取该化学突触模型，其表达式如式（ 3）所示

式中：Isyn为突触后电流，GS为突触后电导，ES为突触可逆电位，VP为突触后保持电位，V1、V2分别为前后神经元的膜电位，-CmS2描述了突触前神经元动作电位产生的电容电流，GS（ VP-ES+V1-V2）描述了通过突触后配体门控通道的离子电流。

由Leonid 化学突触连接的2 个HH 神经元数学模型如式（ 4）

式（ 4）说明了通过Leonid 化学突触耦合的神经元中神经元膜电位和突触电流之间的数学关系。 用其来描述由多个单神经元构成的具有非线性相互作用的复杂网络。式中：i 和j 表示网络中神经元的编号。根据所得到的数值解可以计算出不同情况下的膜电压和相应的突触电流。 这个耦合系统方程为单个神经元膜电位方程右侧增加一项突触电流Isyn（ j，i）。 在方程中i 是突触前神经元，j 是突触后的神经元。 突触电流的数值是由前后神经元膜电位确定的， 且突触电流的流向是j 到i，即突触电流仅对突触后神经元产生影响。 每一个神经元都能接受刺激信号Iext而不产生任何影响，在神经元仅传导刺激，没有外界电流刺激的情况下，对应的Iext值为0。 A（ i，j）是取1 或者0 的连接矩阵，值是1 说明神经元j 和神经元i 存在连接，否则，说明2 个神经元之间没有联系；Gji是突触后的电导。

由电突触连接的2 个HH 神经元数学模型如式（ 5）所示

式中：i、j 是网络中的神经元的编号，Iext表示外部刺激电流的大小。前、后膜电位的差值与缝隙电阻相乘取得突触电流值，突触电流作用于2 个互相耦合神经元。

通过建立HH 神经元和突触耦合的数学模型，为神经元网络仿真建模提供了依据。 本节通过对耦合系统数学模型进行分析， 为后文通过软件对生物神经元网络进行数值模拟做好了铺垫。

1.3 模拟仿真平台

本文基于MATLAB&Simulink 平台进行建模仿真。分别由化学突触和电突触耦合的神经元Simulink 模型如图1 所示。

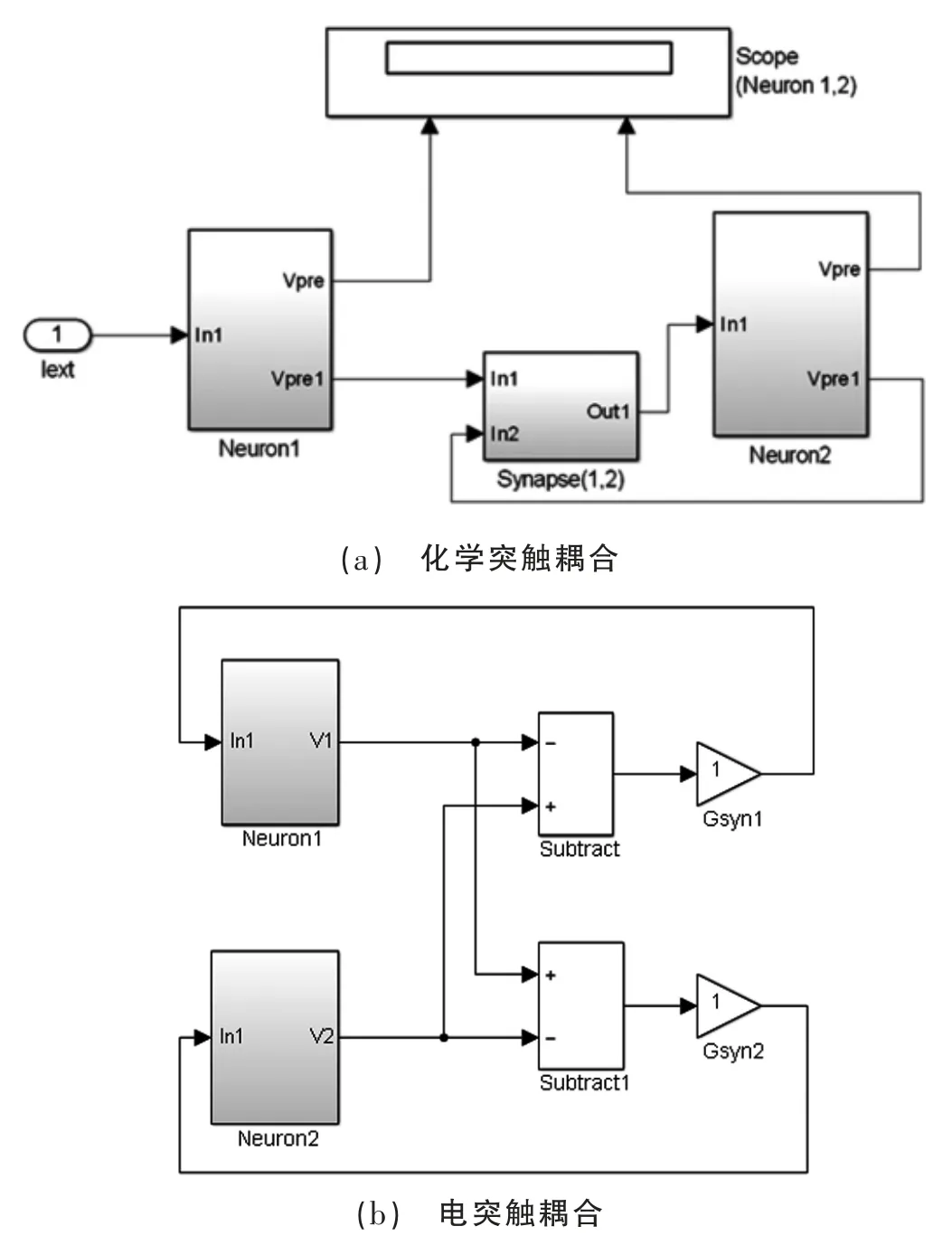
图1 双神经元耦合的Simulink 建模

如图1 所示神经元和突触模块进行了封装处理，在构建神经元网络模型的过程中， 如需增加神经元个数或调整神经元网络的拓扑结构时， 封装好的神经元和突触可根据对应拓扑结果直接连接。 本文在构建神经元网络模型时，采用模块化建模，能直观地反应所建网络模型各模块之间的相互关系。

2 研究结果

在大脑的神经系统中， 神经元网络的连接方式分为规则连接和不规则连接，实验结果表明，真实的生物神经元网络以不规则连接方式为主， 表现为小世界特性。本文通过构建小世界神经元网络，比较研究了分别由电突触和化学突触连接的小世界神经元网络在同一正弦信号刺激下的同步放电特性。

本文构建的神经元网络模型中神经元个数为5，且为全同神经元。 网络中神经元通过化学突触依次有向连接，符合生物神经系统中信息传递结构。以化学突触连接的简单环网和小世界网络为例， 在Simulink 中构建的模型如图2 所示，图中Synapse（ 1，2）表示神经元N1 和N2（ 后文神经元均由编号表示）之间的化学突触，信息由N1 向N2 传递。 小世界神经元网络是在简单环网模型结构的基础上， 不破坏原来环结构的任意一个连接，对网络进行加边处理，且神经元本身不能自连。 小世界神经元网络模型中每个神经元依序与网络中除自身外其他2 个神经元相连， 该模型在简单环网的基础上增加了10 条突触，符合小世界网络特点。 神经元网络的输入信号为正弦波信号Iext=10sin（ 0.1πt）+10，N1 接收刺激信号，其余神经元外加刺激为0，突触后电导（ 耦合强度）取值设置为1 mS/cm2。

图2 化学突触连接的5 神经元网络Simulink 模型

将正弦信号Iext=10sin（ 0.04πt）+10 作为刺激信号输入神经元网络，正弦信号时域波形图如图3 所示。神经元网络中N1 接收刺激信号， 其余神经元外加刺激为零，设置仿真时间t 为100 ms。 图4 为示波器模块观测的由电突触和化学突触连接的神经元网络中N1 和N5 的动作电位波形。

图3 正弦信号时域波形图

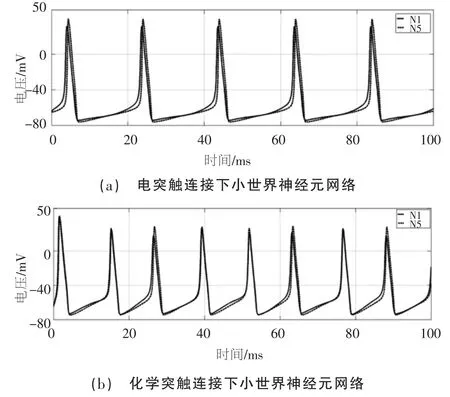
图4 不同突触连接下小世界神经元网络同步放电效果

由仿真结果可以看出， 相同拓扑结构的神经元网络在同一刺激信号下， 神经元都产生了稳定的周期电位，均包含完整的放电过程。电突触连接的神经元网络N1 和N5 动作电位会产生时延，最大时延为1.5 ms；化学突触连接的神经元网络N1、N5 动作电位时延较小，最大时延为0.5 ms，且放电波形不断趋于重合，同时，当输入信号不变， 化学突触连接的神经元网络放电频率提高但依然保持节律性。

3 结论

本研究采用数值模拟的方法， 选取Hodgkin-Huxley 神经元作为神经元网络的基本单元， 分别构建了由电突触和化学突触连接， 符合生物学实际的小世界神经元网络。 对不同类型神经突触连接的神经元网络同步放电特性进行了对比研究。研究结果发现，在同一外加信号的刺激下， 分别由电突触和化学突触连接的具有相同拓扑结构的神经元网络具有不同的同步放电特性。 电突触连接的神经元网络动作电位会产生时延，最大时延为1.5 ms；化学突触连接的神经元网络动作电位时延较小， 最大时延为0.5 ms， 且基本趋于同步。证明在同一刺激信号，相同拓扑结构的神经元网络中， 化学突触连接的网络同步放电特性要优于电突触连接的神经元网络。同时，突触类型的不同可能会改变神经信息的编码方式但不会改变信息传递的可靠性。本文基于Hodgkin-Huxley 神经元模型，构建了具有生物属性的神经元网络， 考虑了真实神经系统中通过电突触和化学突触进行信息传递的过程， 这对后续研究神经信息传递的相关机制提供了一定的便利， 为大脑记忆功能的神经生物学机制提供了实验方法。