一种基于改进深度强化学习的加工成本型铣削参数优化方法
2023-08-21严胜利李俊泓张春林
严胜利,李俊泓,李 浩,张春林
(广安职业技术学院,四川 广安 638000)
制造业的能源消耗随着社会工业化的持续改善而增加[1]。准确预测加工过程中的能源消耗并优化加工参数以提高加工能源效率和节约制造成本具有重要意义[2]。
优化铣削参数的方法[3]包括:响应面法、粒子群优化算法、BP-SA 优化铣削参数的路径、基于深度强化学习的铣削参数优化方法等。这些方法的目的是提高加工过程的能源效率,降低成本,并使铣削加工过程更加精确和高效。而基于深度强化学习的铣削参数优化方法是一种近年来新发展起来的方法,可以考虑加工成本,响应面法和粒子群优化算法是比较常用的方法。曾金平等[4]建立CNC 车床主轴加速能耗模型,并讨论减少这部分能耗的潜在方法。在刀具磨损的不同阶段,考虑切削能耗存在动态变化过程。因此,戚晓楠等[5]通过开发统一切削试验工具磨损和能量图,评估不同切削条件下的刀具磨损率和特定切削能量。为研究实际材料去除所消耗的能量,于硕等[6]在过程水平上定义了一个新概念,净切削比能量,并建立每个完成硬铣加工水平的切削条件和能耗之间的关系。宣鹏举等[7]关注的是热辅助加工的能耗。此外,表面质量也是加工过程优化的关键目标之一。卢家锋等[8]不仅建立不锈钢铣削的经验能耗模型,还基于RSM 方法建立表面粗糙度的预测模型,并优化节能和高质量加工的工艺参数。Fatoorehchi 等[9]使用反演分析方法分别建立切削力模型、残余应力模型、工具寿命模型和表面粗糙度模型。然而,随着加工能耗预测模型越来越完善,模型的计算也变得更加复杂。每个机床加工部件的能耗公式系数很多,分析和实验校准的工作量增加。
本文提出的铣削参数优化方法基于深度强化学习,该方法具有较大的搜索时间优势,并且采用粒子群优化算法可以获得最佳优化效果。
1 研究基础
1.1 反向传播神经网络模型解析
反向传播神经网络[10](Back Propagation Neural Network,BPNN)是一种人工神经网络,是一种多层前馈神经网络,可以用于监督学习。BPNN 通过使用反向传播算法来训练网络,该算法使用梯度下降法来最小化误差函数。其网络结构通常包括输入层、隐藏层和输出层,其中隐藏层可以有多个。BPNN 模型的训练过程是在输入数据和期望输出之间进行的,通过不断地调整神经元之间的连接权重,使得网络的输出结果逐渐逼近期望输出。BPNN 模型在分类、回归等任务中具有广泛的应用。
反向传播神经网络模型优点在于高效性。BP 神经网络的示意图模型如图1 所示。
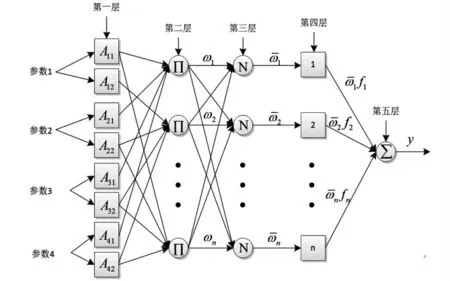
图1 BP 神经网络的示意图模型
1.2 粒子群算法解析
粒子群算法[11]是一种群体智能优化算法,其灵感来源于鸟群或鱼群等生物的行为。该算法通过模拟粒子在搜索空间中的移动来寻找最优解。每个粒子代表着搜索空间中的一个解,其位置和速度可以通过一定的规则进行更新,使其逐步向最优解靠近。在算法迭代过程中,每个粒子可以根据自身的最优解以及全局最优解进行位置和速度更新,以期望找到更优解。粒子群算法寻优过程如图2 所示。
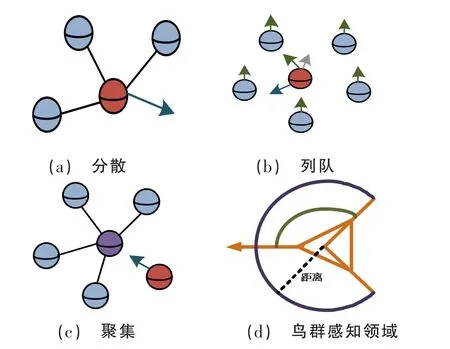
图2 粒子群算法寻优过程
2 复合优化算法的参数优化解决方案
本文根据建立的目标函数模型和约束方程,上述模型均为非线性方程,如果采用传统的优化算法(如遗传算法、蚁群算法等),计算复杂,结果容易陷入局部最优。因此,引入一种组合优化算法,结合APSO(Adaptive Particle Swarm Optimization,APSO)和NGSA-II,以优化模型,获得更精确的处理参数组合,新的组合优化算法可以充分发挥粒子群优化的收敛性和遗传算法的种群多样性。
2.1 自适应粒子群算法(APSO)
APSO 算法是一种群体智能算法,认为粒子处于n维空间中,根据一定规则传递信息,并根据信息的变化改变自身状态生成的自组织行为。如图3 所示为APSO算法中粒子之间信息传递模型。
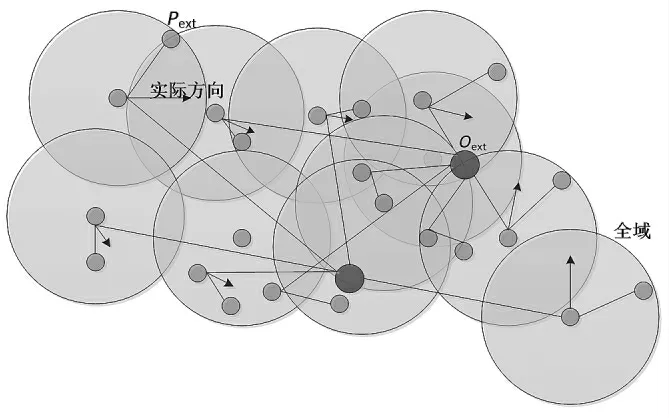
图3 APSO 算法中粒子之间信息传递模型
该算法的步骤如下。首先,初始化一定规模的粒子群,当粒子群初始化时,每个粒子都有3 个属性:适应度P,速度V 和位置X。其次,每个粒子将比较其当前位置的适应度值与其历史中最佳适应度值pid,并将比较后的更好值作为当前最佳位置pext,否则不进行任何变化。粒子可根据式(1)和式(2)来更新速度和位置,直到达到设定的终止条件。
式中:w 为惯性权重因子,νid为粒子的速度,νid∈[-νmax,νmax],c1、c2为学习因子,通常取c1=c2=2,r1d、r2d为相互独立的均匀分布在[0,1]上的随机数,xid为当前粒子位置。
2.2 改进的遗传算法
改进的遗传算法NSGA-II 采用非支配解排序方法和拥挤距离计算,并增加BPNN 神经网络思想的精英策略。
2.2.1 基因编码
基因编码是遗传算法设计中的关键问题。编码方法必须考虑染色体的有效性、可行性、解空间表示的完整性。在NSGA-II 算法中,设备、工具和工艺顺序的选择需要在部分编码方法中合理反映。对于处理参数的优化,采用编码机制,种群中每个个体都有3 个子串。第一个分子串是工步号,第二部分表示相应的工具号,第三部分表示对应于工步的处理特征的平方表面编号。
2.2.2 交叉处理
改进的遗传算法对于不同的子串,遗传处理是不同的。相比于单点交叉,双点交叉可以有效地减少位置偏差,而不会引入分布偏差。首先随机选择2 个染色体F1 和F2 作为亲代染色体,在F1 中随机生成2 个交叉点,然后将F1 的相应左右部分复制到后代染色体C1的同一位置,最后从F2 中移除F1 的左右部分,在C1染色体上复制原始后代C1 的一部分基因。以相同的方式,可以获得另一个后代的C2 染色体。
2.2.3 突变处理
突变发生在交叉之后。突变是指将个体染色体编码字符串中某个位点的基因值替换为该位点的其他等位基因,从而形成一个新个体。
2.3 基于APSO 和NSGA-II 的组合算法
与NSGA-II 相比,APSO 更加简洁,收敛速度更快。然而,更新粒子位置主要依赖于将其自身位置与其周围位置以及当前种群中的最优位置进行比较。这种模式相对简单,使得其收敛速度在后期计算中不够高效。
NSGA-II 具有4 个不同的进化步骤,包括选择、交叉和变异,增加了解决方案的多样性。当NSGA-II 解决到一定范围时,会导致冗余迭代的低效处理,计算时间过长,解决效率低。因此,本研究将APSO 和NSGAII 结合起来,融合BPNN 思想,以提高算法效率。
组合算法的步骤总结如下。
步骤1:初始步骤。在可行区域内,APSO 生成p 个粒子并演化kmax度代数。所有粒子根据目标函数的值排序,然后将种群分为2 个子种群。优化的p/2 个粒子用作APSO 处理的初始种群p1。剩余的p/2 个粒子用作新一代染色体p2进行NSGA-II 处理。
步骤2:进化步骤。在寻找最优解的过程中,子种群p1 的位置和速度可根据式(3)—式(4)进行更新。
式中:xid为位置向量,νid为速度向量,k 为迭代次数,w为惯性系数。根据式(5)可知,p2中染色体的选择概率与第i 个个体的目标函数值Fi有关。
步骤3:自适应处理。在传统的遗传算法中,由于种群规模有限,大多数个体都具有良好的目标函数值,并且这些良好的个体会被复制。其他个体在经过几次进化迭代后被淘汰。但是当适者生存的过程失去控制时,缺乏多样性和近亲繁殖会出现,交叉和突变处理将失去效力,使算法更难跳出局部最优。
从上述的分析可以得知,基于种群早熟标记的适应性处理过程如下。程序开始时,将初始交叉概率和遗传概率赋值为1。当算法计算出种群参数的目标函数值时,也会计算出交叉概率和遗传概率。使用初始交叉概率和遗传概率进行交叉变异,生成下一代的种群,计算新一代的种群参数。如果该参数大于预设值,这表明种群趋向于早熟,则使用交叉概率和遗传概率重新生成一个新的种群;否则,初始交叉概率和遗传概率仍然保留。在一定程度上,适应性处理可以有效地解决算法的早熟现象。为了确保每一代的最佳个体不会被破坏,算法收敛于全局最优解。
3 实验分析
实验设备:立式加工中心(型号:VDL-850A),VDL-850A 相关规格和参数见表1。根据第2.2 节和第2.3 节的分析,分别得到多目标函数的能耗目标函数和成本目标函数,并在实际约束条件下建立多目标函数的优化模型。在使用Matlab 编程和优化多目标函数时,需要在程序中输入相关参数,并输出最优解信息和最优目标值组合。对于能耗目标函数,使用Matlab编程和优化多目标函数,在程序中输入目标函数的相关参数,对于成本目标函数,根据公式需要将相关参数输入Matlab 程序中。

表1 VDL-850A 相关规格和参数
根据多目标函数模型和加工要求,设置相关参数如下。
1)工件材料:零件材料为45 钢。
2)刀具:直径为16 cm,齿数为3 cm 的高速钢端铣刀,主角度。
3)加工要求:粗铣40 mm×40 mm 尺寸的台阶面,铣削深度为4 mm,铣削宽度为20 mm,长度为40 mm,在加工过程中使用切削液。
3.1 权重设置
基于先前建立的组合算法,只需要从第二步骤开始,以便获得每个给定目标函数的不同权重系数。为方便解决多目标优化问题,通常难以同时获得多个目标函数的最优解。为解决这个问题,将多目标函数转化为单目标函数。线性加权法是最简单的计算方法,权重可以通过主观评价每个目标的重要性来分配。其中λ1+λ2=1,λ1和λ2分别是过程成本加权系数和能耗加权系数。在本研究中,这2 个因素在优化过程中被视为是同等重要的。因此,这里将权重设置为λ1=λ2=0.5。然后,新的目标函数可以用作评估函数。选择不同的权重组合进行模拟分析和比较。
3.2 通过组合算法优化处理参数
为验证所提出方法的有效性,应用组合优化算法解决多目标线性模型问题。使用Matlab 编写程序,分别以多目标、单一目标最小成本和单一目标最小能量作为处理参数优化的目标。组合算法参数设置如下。
①设置初始种群数为30。②迭代次数k 为150,xid取0.9。③vid取0.4。以节能和低成本为优化目标,组合算法的迭代收敛过程如图4 所示。通过以上分析,分别以多目标、单一目标最小成本和单一目标最小能量作为处理参数优化的目标。
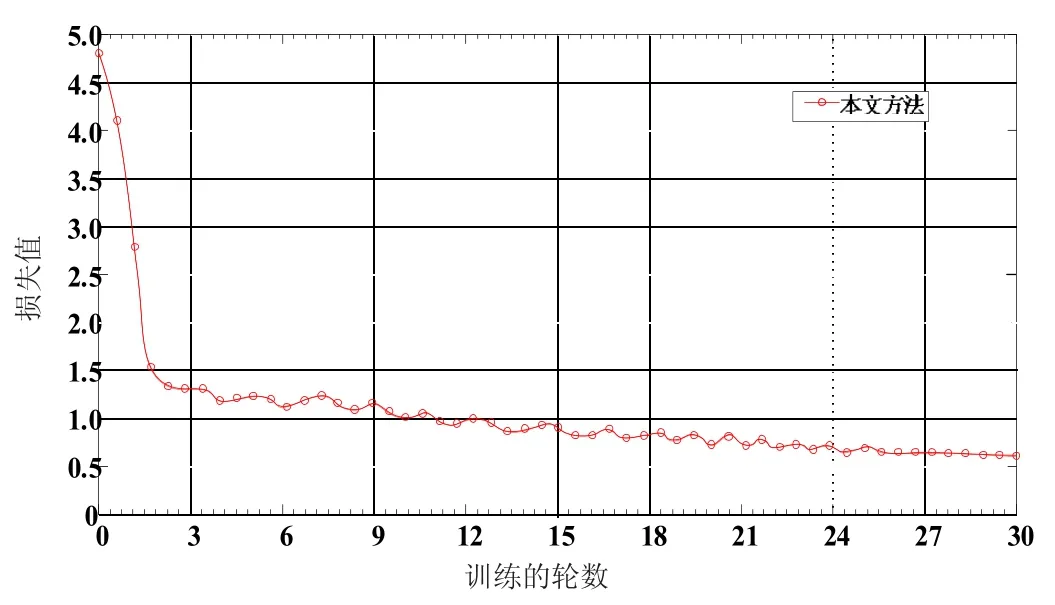
图4 组合算法的迭代收敛过程
3.3 比较研究
本研究提出的多目标优化模型与单目标优化模型进行比较,可得以下结果。
1)以低加工成本为优化目标,铣削速度为28.51m/min,每齿进给为0.09 mm/z,加工时间为45.2 s,加工成本为46.17 元人民币。单目标优化铣削速度较低,主轴转速慢,刀具磨损小,加工成本低。但由于加工时间长,加工所需能量消耗达到3.475×105 J,因此,本文方法整体成本比单目标优化模型低。
2)以节能为优化目标,铣削速度为32.07 m/min,每齿进给为0.09 mm/z,加工时间为42 s,能量消耗为3.468×105 J。铣削速度和主轴转速更快,加工时间更短,导致加工能量消耗更少。然而,单目标优化模型由于快速铣削速度导致刀具磨损增加,加工成本达到46.94 元人民币,本文方法比单目标优化模型成本低。
4 结束语
在加工过程中,工艺参数的选择直接关系到待加工零件的生产效率、成本和能耗。合理的工艺参数不仅可以提高生产效率,降低生产成本,还可以减少加工过程中的能耗。因此,设计优秀的组合算法,解决加工过程中能耗随加工过程的动态变化问题,实现既能满足加工中心节能降耗要求,又能兼顾其主要经济指标的优化,方法意义重大。
本文首先设计了反向传播神经网络模型,采用APSO 算法、NSGA-II 算法与自适应粒子群算法的复合优化算法,提出优化铣削参数解决加工能耗的方案,并完成了基于APSO 和NSGA-II 的组合算法与单独的APSO 方法或NSGA-II 方法比较。采用以VDL-850A型号的立式加工中心为实验设备,针对能耗目标函数,使用Matlab 编程和优化多目标函数,分别以多目标、单一目标最小成本和单一目标最小能量作为处理参数优化的目标。
本研究提出的多目标优化模型与单目标优化模型进行比较,以低加工成本为优化目标进行分析,铣削速度较低,主轴转速慢,刀具磨损小,加工成本低。以节能为优化目标进行分析,铣削速度和主轴转速更快,加工时间更短,导致加工能量消耗更少。因此,本文方法无论从低加工成本目标和节能优化目标相比,均比单目标优化模型成本低。
