水准测量的中误差计算与i 角检验
2023-08-21刘洪熙
1 引言
得益于信息科技的进步,越来越多的测量测绘人员,在进行水准测量作业后,直接采用软件进行计算和分析测量成果,软件的便利与快捷也导致测量人员忽略了手动计算中误差的计算方法。 标准和规范中对测量精度的要求,是以测站高差中误差或高程中误差来控制测量精度的指标。 因此,现场测量人员都应该熟悉掌握中误差的计算方法,在作业的同时,现场可以检验测量的成果,当发现精度指标不满足要求时,可以及时进行复测,避免不必要的返工重测,降低测量成本增加的可能性,提高测量精度,为质检人员提供可靠依据。 本文的中误差计算公式也可为信息科技的发展提供了更多参考, 为软件开发人员提供更多的中误差计算编程方法。同时,本文还将介绍水准仪i 角(水准仪的视准轴在垂直方向与水准轴的夹角称为i 角)的检验和校正,通过对水准仪i 角校正的误差分析,提出相关理论改善来校正方法,可以有效改进水准仪i 角的校正结果准确度。
2 中误差计算公式推理
在进行水准测量时,系统误差具有规律性,可以通过测量手段找到并进行消除,偶然误差是没有规律且不好避免的,因此,本文所讲的误差为偶然误差[1]。
后视点A 高程为HA, 水准仪读数的真值为hA,A 点的测量误差为hAi,前视点B 的水准仪读数真值为hB,B 点的测量误差为hBi。
AB 点的高差等于A 点读数减去B 点读数, 即hAB=hA+hAi-(hB+hBi)。
AB 点 的 高 差 误 差 表示 为:ΔAB=hAi-hBi, 假设 测 量 次数为2, 求出的高差误差为ΔAB, 那么高差中误差表示为m'ab=。
B 的高程HB等于A 点高程加AB 点高差,即HB=HA+hAB;后视点A 的高程误差HAi,中误差为ma′,B 点的高程误差表示为HBi=HAi+ΔAB,当后视点A 为已知点时,后视点中误差ma′=0,则B 点高程中误差表示为。
当水准路线为闭合水准路线或附和路线时, 需要考虑闭合差对每个测站的影响, 将视距作为权P 考虑对每个测站的影响因数,经过权的分配,每个测站代入改正数V,进一步减小测量误差,提高最终成果的精度。
则高差中误差表示为:
高程中误差表示为:
式(1)~ 式(2)中,i 为测站;Pi为i 测站的权值;Vi为i 测站的高差改正值;P1~i为第1~i 测点的权值和;V1~i为第1~i 测点的高差改正值和。
在闭合或附和水准测量中,闭合差或附和差为Δ,水准路线总长度为L,第i 测站的视距长度为Li,第1~i 测站的累加视距长度为L1~i。 那么,,,。
将Pi、Vi、P1~i、V1~i替换,任意测站的 前视点(转点)用n 表示,则中误差计算公式:
任意测站的高差中误差表示为:
任意测站的转点高程中误差表示为:
对测站中存在的中间测量点,中误差计算公式:中间测量点的高差中误差表示为:
中间测量点的高程中误差表示为:
式(5)~ 式(6)中,mn-1为当前测站后视点的高程中误差;P′i为中间测量点的权值;L′i为中间测量点与后视点的视距和。
3 中误差计算成果的验证
为了对本文推理的公式结果的准确性进行验证, 选择目前市场上应用较为广泛、 认可度比较高的一款平差软件Adjust Level, 在实际工程项目中对同组数据进行计算结果比对。
案例1:浦东新区惠南镇某养老院项目竣工,需要对使用期间的建筑物进行沉降观测,按照规范要求,在施工影响范围以外布设3 个基准点,点号为BM01~BM03,对建筑物四角及沉降缝、 中间部位布设沉降观测点共计12 点, 点号为J01~J12。
该项目沉降观测等级采用三等水准测量精度控制, 建筑物沉降观测点测站高差中误差精度指标为1.5 mm,视线长度小于或等于75 m, 大于或等于3 m, 前后视距差小于或等于2.0 m, 采用数字水准仪每点重复测量2 次, 采用光学水准仪时,进行基本分划和辅助分划分别读数,两次读数所测的高差之差限差为3.0 mm,观测前i 角不超过20 s(三等)。
按照以上精度要求,采用索佳SDL03 数字水准仪进行测量,现场采集数据,本文利用推理的中误差公式,对原始数据进行平差计算,并计算中误差,成果如表1 所示。

表1 计算成果表
通过计算,成果总结如下:(1)环线长度327.646 m,闭合差-0.00139 m,测站数为6 站;(2)最大高程中误差0.000 96 m,点号J06,最小高程中误差0.000 39 m,点号BM02;(3)平差后高差中误差,最大高差中误差0.000 67 m,后视点号TP01,前视点号J12。
将原始数据1.csv 导入水准平差软件Adjust Level 进行计算,以经典平差方式自动计算,计算成果如图1~图2 所示。
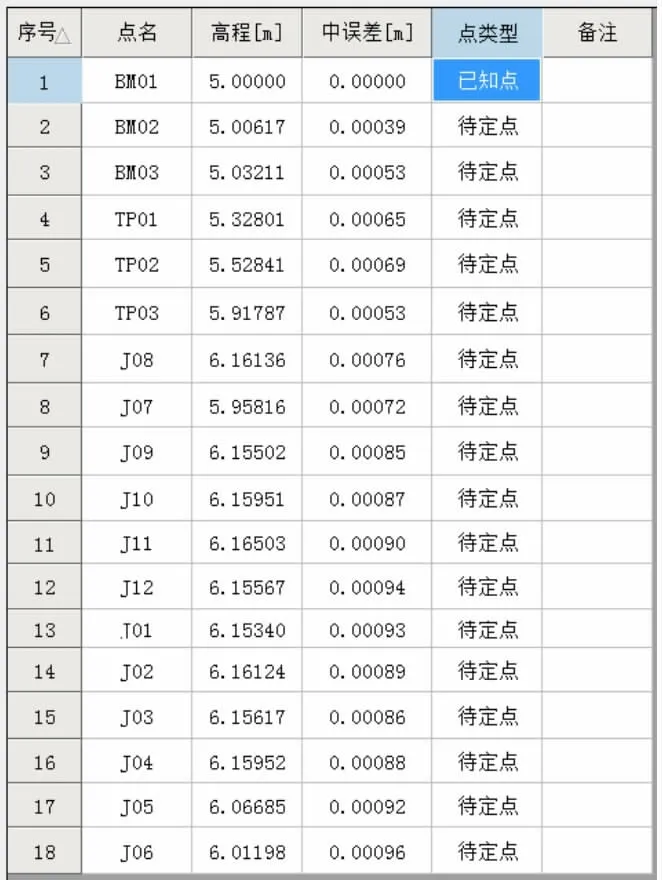
图1 平差结果
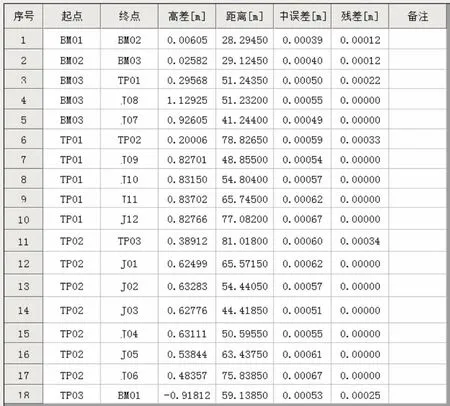
图2 高程残差
通过对比可以发现, 本工程在使用相同原始数据的情况下,AdjustLevel 软件自动计算的成果数据与本文公式计算结果相同。
4 普通水准仪的校正误差分析
当对水准仪i 角进行检验时,实际上是对水准管轴平行于视准轴(i 角)的检验。 首先,假设人为操作误差为零,对于普通水准仪i 角(适用于三、四等水准测量)检验如图3 所示。

图3 普通水准仪i 角检验
校正过程如下:将仪器架设在A、B 尺中间J1位置,测量并计算出理论真值高差为h0=a1′-b1′=a1-b1,然后将仪器架设在J2处,测出A、B 尺读数a2、b2,高差h1=a2-b2,则调整值为b2+h0(图3 中的a2″),i 角= h1-h0×ρ/D1(“ρ” 为1 弧度, 约等于206 265′),转动十字丝环的螺丝,使读数a2等于调整值a2″[2]。
由图3 可以看出,a2″并不是A 尺的理论真值读数值,仪器校正过后仍存在误差,J2至B 尺的距离2 m, 假设i 角误差20″,A、B 尺距离80 m,则测量值b2与理论真值b2′之间差值为δ=i/ρ×D2=20/206 265×2 000≈0.19 mm,也就是说i 角校正时的理论计算的基础本身就存在0.19 mm 误差。
首次仪器校正后,再次进行i 角检验,测站J1高差为h0,测站J2高差为h1′, 则,J1与J2的高差之差为h1′-h0=δ-δ×D1/(D1+D2)≈0.189 3 mm,i 角= h1-h0×ρ/D1≈0.488″。 此时我们发现虽然对仪器进行了校正,但在理论上并没有真正对i 角归零;假如i 角的首次检验值为60″,校正之后的i 角值将会等于1.46″,对于测量距离60~80 m 的误差为0.42~0.57 mm,在测量中误差会根据测站的传递进行累加,因此影响还是很大的,而且人为操作误差不可能为0,实际i 角校正中,真实误差会相差更多。
在实际校正水准仪时, 应该消除水准仪的理论误差δ,使其只存在人为操作误差,将i 角误差减少到最小。 当仪器在J2时,A 尺理论真值读数a2′=a2-(D1+D2)×i/ρ, 调整十字丝环使a2=a2′,即可完成i 角的校正,同时也消除了理论误差δ。
5 精密水准仪的检验和校正
普通水准仪主要是用于三、四等水准测量,精度要求相对不高, 但对于一、 二等水准测量, 要求精密水准仪i 角小于15″,规范要求的测量精度非常严格,精密水准仪i 角检验如图4 所示[3],校正方法与普通水准仪不同,普通水准仪i 角检验原理中仪器距离两尺之间距离较远, 读数的清晰度不如精密水准仪i 角检验原理,这样就增加了读数误差(视差),也就是说相同等级测量的情况下,精密水准仪i 角检验过程的精度要高于普通水准仪的i 角校正的精度。 因此,有必要整理一套简便且精度较高的精密水准仪校正方法。
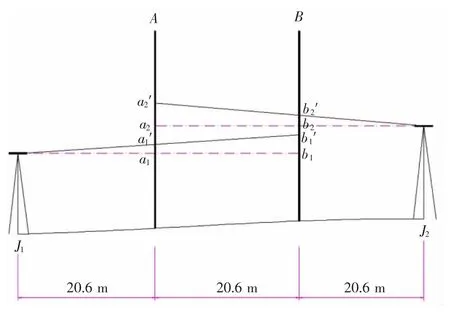
图4 精密水准仪i 角检验
精密水准仪i 角检验原理如图4 所示, 在J1位置测量得出h1=a1′-b1′, 在J2位置测量得出h2=a2′-b2′,A、B 尺高差真值应为h0=(h1+h2)/2,Δ= h1-h0/2,i=Δ×ρ/20 600。
为了校正时更加便捷, 不在烦琐地去布设测点和量取距离,最好的方式就是继续利用目前已经布设好的J1、J2、A、B 位置,在水准仪i 角校正时,扶尺人员操作误差暂忽略不计,那引起i 角校正误差的原因主要还有两点:人为测量误差、读数误差 (视差)。 按照图4 路线,J1—A—B—J2之间距离20.6 m,仪器读数最远距离为2×20.6=41.2 m, 小于普通水准仪的D1+D2=62~82 m,距离的改变带来的是视距的减小,物体成像更加清晰,使测量人员在读数时,可以更加准确地读数,最大程度减小了视差,将仪器分别架设在J1、J2两处测量读数,计算出高差真值h0, 在将仪器架设在J2位置, 理论真值a2=a2′-2Δ或a2=a2′-20.6×2×i/ρ,调整十字丝环的螺丝,使读数a2′=a2,即可完成i 角的校正。 理论上来说,此方法消除了i 角误差,减小了视差,每次校正后i 角无限趋于零。
6 结语

