基于多角度表观反射率模型的交叉定标方法
2023-08-21张艳娜郭傅翔韦玮李新
张艳娜,郭傅翔,韦玮,李新
(1 安徽工程大学 电气工程学院,芜湖 241000)
(2 中国科学院合肥物质科学研究院 通用光学定标与表征技术重点实验室,合肥 230031)
(3 中国科学技术大学,合肥 230026)
0 引言
光学遥感器在轨运行时易受空间环境变化等影响导致性能改变,通过高频次的辐射定标来跟踪载荷的在轨状态,及时校正载荷性能变化,可以保证观测数据的准确性,为定量产品反演和多载荷融合应用提供基础的技术支撑[1-2]。在太阳反射波段,目前常用的高频次定标方法包括星上定标[3]、交叉定标[4]、稳定目标跟踪[5]、自动化定标[6-7]等,其中星上定标精度较高且应用广泛,主要利用卫星上搭载的灯、板等定标器实现载荷的在轨高频次定标[3,8]。但是由于星上定标器的性能参差不一,载荷之间的观测数据量值基准有所差异,导致不同载荷观测和反演的定量产品存在一定的系统误差[8-9],限制了星星之间的数据比对和融合应用。为此,近年来国内外相继开展了空间基准载荷的研究,通过在空间建立低温辐射计[10-11]、相关光子等[12]辐射初级基准的传递链路,将辐射初级基准传递到高光谱对地成像仪,利用高光谱对地成像仪和待定标载荷进行交叉定标实现量值传递,来提高载荷之间的在轨辐射定标精度和数据一致性。
在进行空间辐射基准交叉定标传递时,常以地球稳定目标作为交叉点,通过同步星下点观测(Simultaneously Nadir Observation,SNO),利用视场匹配、时间匹配、光谱匹配、角度匹配和大气校正等手段,实现待定标载荷的辐射基准传递[4]。理论上通过SNO 交叉定标,待定标载荷可达到与基准载荷相当的定标精度,但是受限于基准载荷和待定标载荷之间轨道不同,载荷之间的观测角度存在较大差异,因此满足SNO 交叉匹配条件下的定标频次有限[13],为了提高定标频次,目前多采用地表的双向反射分布函数(Bidirectional Reflectance Distribution Function, BRDF)模型进行角度匹配[4,14],来扩大角度适用性,减小地表BRDF 效应带来的角度匹配误差。地表的BRDF 模型常采用人工现场实测的方式获得[4],但是在一些难以进行地面试验或者缺乏地面高光谱BRDF 模型的国内外定标场,角度匹配成为限制交叉定标频次和精度的重要因素[14]。为此,国内外研究人员开展了基于大气层顶表观反射率模型的定标研究,利用高精度的表观反射率数据构建稳定目标场模型,用于交叉定标[15]或绝对辐射定标[16],但是目前主要是针对小角度近垂直观测的载荷,难以直接应用在角度差异较大的空间基准传递中,限制了空间辐射基准在多星多载荷中的高频次应用。
本研究针对空间辐射基准传递交叉定标中的角度匹配对定标频次和精度的影响,提出了基于多角度表观反射率模型的交叉定标方法,利用高精度载荷的长时序多源数据,构建稳定目标场的多角度高光谱表观反射率模型,并利用该模型基于基准载荷中分辨率成像仪(Moderate Resolution Imaging Spectroradiometer,MODIS)开展了风云三号D 星(Fengyun 3D satellite,FY3D)中分辨率光谱成像仪Ⅱ型(Medium Resolution Spectral Imager Ⅱ,MERSI-Ⅱ)的交叉定标应用与比对,可以不依赖于人工地面试验数据实现大角度条件下的交叉定标,及时跟踪和校正载荷的在轨辐射变化。
1 基本原理
通过构建稳定目标场的多角度表观反射率模型开展空间辐射基准交叉定标,将初级基准的辐射量值传递到待定标载荷,具体原理如图1 所示。在进行空间辐射基准交叉定标时,首先对基准载荷和待定标载荷开展观测区域匹配,采用稳定目标场作为地面交叉定标目标,然后进行云剔除获取晴空影像,最后进行时间匹配,减小大气条件非一致性带来的偏差。

图1 基于表观反射率模型的交叉定标原理Fig. 1 Cross calibration principle based on the apparent reflectance model
在进行角度匹配时,采用国外多角度、高精度载荷Terra/MODIS、AQUA/MODIS 自2008—2019 年共11 年的观测角度、太阳角度和表观反射率,分组进行多角度模型构建。基于稳定目标场的准不变特性,忽略时间维场地的变化,利用Hyperion 的平均光谱表观反射率数据构建适用于400~2 400 nm 波段的光谱匹配函数。最终构建的多角度高光谱表观反射率模型为
式中,ρMODEL为模型计算的稳定目标场的表观反射率,θs为卫星过境时刻的太阳天顶角,θv为卫星过境时刻的观测天顶角,φ为相对方位角,λ0为观测通道的中心波长,Kvol为体散射核,Kgeo为几何散射核,fiso、fvol、fgeo为各项核系数,分别表示各向同性散射、体散射和几何光学散射所占的权重,S(λ0)为光谱匹配因子,为
ρHy为Hyperion 的平均高光谱表观反射率,R(λ)和Rr(λ)分别为待定标载荷和基准载荷的光谱响应函数。
式(1)所示的表观反射率模型主要有以下特点:1)角度分组建模:利用表观反射率与卫星观测角度和太阳角度的关系,将Terra/MODIS、AQUA/MODIS 的表观反射率数据分为16 组角度区间(其中天顶角8 组,方位角2 组),拟合得到16 组模型参数,能够适用于天顶角0°~60°角度差异范围内的大角度交叉定标。2)高光谱匹配:将高光谱卫星Hyperion 多季节的大气层顶表观反射率光谱数据进行平均,作为基准光谱开展光谱匹配,使该模型的适用范围覆盖400~2 400 nm 整个波段载荷的定标。
基于式(1)的表观反射率模型开展待定标卫星的表观反射率计算,即
式中,ρTOA为待定标载荷经交叉匹配后计算得到的表观反射率,ρMODEL为利用模型计算的待定标载荷的表观反射率,ρMODEL-r为利用模型计算的基准载荷的表观反射率,ρTOA-r为基准载荷实测的表观反射率。由此可根据式(4)计算待定标卫星的定标系数,D为实测值,D0为冷空观测值,Cal 为定标系数。
2 交叉定标应用
2.1 应用载荷与交叉场地
由于国内外的空间基准载荷均在研制阶段,难以开展应用。为了对基于多角度表观反射率模型的交叉定标方法进行验证,采用国外高精度载荷AQUA/MODIS 作为基准载荷,对国产卫星风云三号D 星上搭载的多角度观测载荷MERSI-Ⅱ开展交叉定标。MERSI-Ⅱ于2017 年11 月发射,包含16 个可见光-近红外通道、3 个短波红外通道和6 个中长波红外通道,主要任务为地球海洋、陆地、大气等环境要素的动态监测[17]。采用的交叉定标通道是FY3D/MERSI-Ⅱ的1、2、3、4、6、7 共6 个通道,具体参数和对应的AQUA/MODIS的观测通道如表1 所示。
采用难以获得人工实测数据的国外稳定目标场利比亚4 作为交叉点,利比亚4 是国际卫星对地观测委员会(Committee on Earth Observation Satellites,CEOS)推荐的准不变定标场,如图2 所示,选取中心位置(28.55°N,23.39°E),大小为75 km×75 km 的场地作为定标区域(图中红色方框区域),地表空间非均匀性小于2%,地表年非稳定性优于2%,气溶胶、水汽、臭氧含量较为稳定,存在一定的季节性变化特点[18]。根据多角度表观反射率模型构建原理,利用长时间序列的MODIS 和Hyperion 载荷数据,完成了式(1)所示的共16 组的多角度、高光谱表观反射率模型的构建。

图2 利比亚4 场地图Fig. 2 Site map of Libya4
2.2 基于模型的交叉定标应用
在利用多角度表观反射率模型开展交叉定标时,首先观测2019—2020 年区域匹配提取基准载荷和待定标载荷利比亚4 场地的数据,并进行云剔除获得晴空条件下FY3D/MERSI 和AQUA/MODIS 两载荷对应通道的表观反射率,如图3 所示。
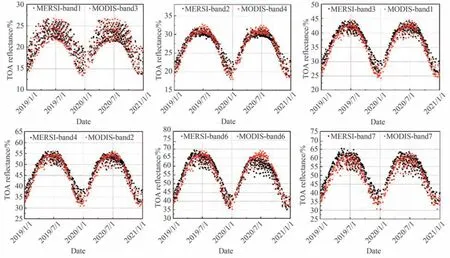
图3 MERSI 和MODIS 在利比亚4 的表观反射率Fig. 3 Apparent reflectance of MERSI and MODIS at Libya 4
然后进行观测时间匹配,提取MERSI 和MODIS 观测时间在30 min 内的观测数据,减小大气条件非一致性带来的偏差。在30 min 的观测时间差内,观测天顶角小于60°的MERSI 和MODIS 观测影像对共205 个。如图4 所示,两载荷观测天顶角的差异从0.49°到56.87°,两载荷观测方位角的差异从0.04°到235.68°。其中,MERSI 和MODIS 的观测天顶角和观测方位角差异在5°以内的影像对共26 个。

图4 MERSI 和MODIS 观测天顶角、方位角的角度偏差Fig. 4 Zenith angle and azimuth angle angular deviation of MERSI and MODIS
对观测天顶角差异在0°~60°范围内的205 个影像对开展交叉定标,基于多角度高光谱表观反射率模型的定标原理,具体步骤为:
1)将MERSI 的观测天顶角和方位角、太阳天顶角和方位角输入模型,得到各个通道模型计算的表观反射率;根据模型计算结果对Hyperion 的光谱线进行比例平移,得到全谱段的光谱表观反射率;将全谱段表观反射率卷积到MODIS 的观测波段,得到MODIS 各个通道的表观反射率ρMODEL;
2)将MODIS 的观测天顶角和方位角、太阳天顶角和方位角输入模型,得到表观反射率ρMODEL-r;
3)根据MODIS 的实测表观反射率,利用式(3)即可计算得到MERSI 的交叉表观反射率ρTOA;
4)结合MERSI 的观测值,根据式(4)计算得到定标系数Cal。
根据上述步骤计算得到MERSI 在2019—2020 年6 个观测通道的交叉定标系数,如图5 所示,通道1~4无明显衰减,通道6 和7 随时间有一定的衰变趋势。各波段定标结果均有一定的季节性变化趋势,由于交叉定标存在一定的时间差异,会受到不同时间大气变化、不同季节大气模式的影响,这与采用稳定目标场进行跟踪定标产生的季节性波动现象一致[5]。
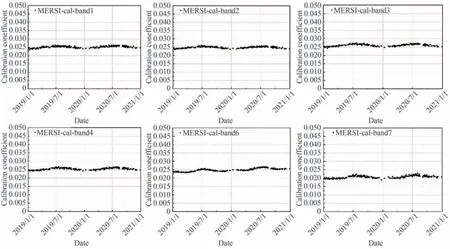
图5 FY3D/MERSI-II 的定标系数Fig. 5 Calibration coefficients of FY3D/MERSI-II
3 结果验证与分析
为了验证基于多角度高光谱表观反射率模型交叉定标结果的准确性,采用与传统的严格角度限制的SNO 交叉定标方法进行比对分析。
筛选MERSI 和MODIS 在观测天顶角和观测方位角偏差5°以内、观测时间偏差30 min 以内的数据,只进行光谱匹配不进行角度匹配,利用式(5)直接计算交叉定标系数。
式中,ρTOA-MODIS为基准载荷MODIS 实测的表观反射率,RMERSI和RMODIS分别为MERSI 和MODIS 的光谱响应函数。
利用式(5)共完成26 次的SNO 交叉定标,与基于多角度表观反射率模型的交叉定标方法进行比对,各通道的定标系数结果和相对偏差如图6 所示。左列图中黑点为各个波段基于多角度表观反射率模型的205 次定标系数,红点为严格角度匹配的26 次交叉定标系数,右列图为相对偏差曲线。


图6 交叉定标系数比对和相对偏差Fig. 6 Cross calibration coefficients and relative bias
由图6 可以看出,采用SNO 交叉定标与本研究采取的基于多角度高光谱表观反射率模型的交叉定标,在测量趋势上具有较好的一致性,其中1、2、3、4 通道相对偏差结果均在4%以内,第6、7 通道相对偏差结果在5.5%以内。计算两种方法的平均相对偏差、标准差如表2 所示,在应用的6 个波段,两种方法的平均相对偏差均在2.1%以内,其中1~6 波段的标准差优于1.7%,7 波段的标准差优于2.52%。但是由图6 可以看出,定标系数具有一定的季节性变化规律,这主要由于稳定目标场的大气特性存在一定的季节性变化规律,在进行大气层顶多角度表观反射率模型的构建时,忽略了时间维的变化,这样会引入一定的大气影响因素,为了消除这种影响,后期应该改进模型,增加大气校正因子来减小大气季节性波动带来的影响。

表2 交叉定标方法比对的平均相对偏差和标准差Table 2 Average relative deviation and standard deviation of cross-calibration results
由比对结果可以看出,采用多角度高光谱表观反射率模型的交叉定标方法,与传统的SNO 交叉定标方法之间具有较好的一致性和准确性,证明了本研究中构建的多角度高光谱表观反射率模型,可以较好地应用于大角度差异条件下的交叉定标,减少对现场测量定标场多角度地表数据的依赖和角度差异对交叉定标结果的影响,显著提高定标频次。在利比亚4 稳定目标场的应用验证了基于多角度表观反射率模型的交叉定标方法的可行性,该方法应用的前提是定标场地具有稳定的地表和大气特性,目前我国卫星定标常用的敦煌国家辐射校正场等目标场的地表、晴空日气溶胶、水汽、臭氧等特性都较为稳定且有一定的规律,因此后续可以在多个稳定场进行推广应用,来进一步验证该方法的适用性。
4 结论
本文针对多星多载荷空间辐射基准交叉定标提出一种基于多角度表观反射率模型的交叉定标方法,利用长时序、多角度、高光谱的国外高精度卫星数据构建了稳定目标场利比亚4 的表观反射率模型,适用于天顶角在60°以内、观测波段400~2 400 nm 以内载荷的多角度交叉定标,通过对2019—2020 年FY3D/MERSI与AQUA/MODIS 开展的交叉定标应用表明,与严格角度限制的SNO 交叉定标方法相比,定标频次由26 次提高到205 次,平均相对偏差在2.1%以内,验证了该定标方法的可行性和准确性。该方法可以应用于高频次交叉定标,能及时跟踪和校正载荷在轨变化趋势,提升遥感数据质量。但是在单点定标的准确性、季节性波动方面还有待进一步的分析和改进,后续将开展国内外多个稳定目标场的建模,通过对多类型载荷开展应用与比对验证,更好地服务于空间辐射基准传递和多星遥感数据融合应用。
